Иерархическая кластеризация в Python [Концепции и анализ]

С увеличением потока необработанных данных и необходимостью анализа концепция обучения без учителя со временем стала популярной. Он используется для извлечения информации из наборов данных, состоящих из входных данных без помеченных целевых значений. Прежде чем мы начнем обсуждать иерархическую кластеризацию в Python и применение алгоритма к различным наборам данных, давайте вернемся к основной идее кластеризации.

Кластеризация в основном связана с классификацией необработанных данных. Он включает в себя группировку различных точек данных, которые наиболее похожи друг на друга. Эти группы называются кластерами, которые формируются на основе определенной метрики сходства или кластеризации.

Введение

Иерархическая кластеризация имеет дело с данными в виде дерева или четко определенной иерархии. Процесс включает в себя работу с двумя кластерами одновременно. Алгоритм опирается на матрицу подобия или расстояния для вычислительных решений. То есть, какие два кластера объединить или как разделить кластер на два. Имея в виду эти два варианта, у нас есть два типа иерархической кластеризации . Если вы новичок и хотите узнать больше о науке о данных, ознакомьтесь с нашими курсами по науке о данных от лучших университетов.

Одним из важнейших аспектов алгоритма является матрица подобия (также известная как матрица близости), поскольку весь алгоритм основан на ней. Существует множество методов близости, которые обсуждаются далее в статье.

Типы

Иерархическая кластеризация бывает двух типов:

1. Агломерационная кластеризация
2. Разделительная кластеризация

Типы соответствуют основной функциональности: способу развития иерархии. Агломератив — это генератор восходящей иерархии, тогда как разделительный — это генератор иерархии сверху вниз.

Агломератив принимает все точки как отдельные кластеры, а затем объединяет их на каждой итерации, по две за раз. Разделение начинается с того, что все данные рассматриваются как один кластер и разделяются до тех пор, пока все точки не станут отдельными кластерами.

В результате получается набор вложенных кластеров, которые можно воспринимать как иерархическое дерево. Лучший способ просмотреть ее — преобразовать заданную структуру в дендрограмму для просмотра иерархии.

Ниже приводится простой пример дендрограммы по сравнению с представлением кластера:

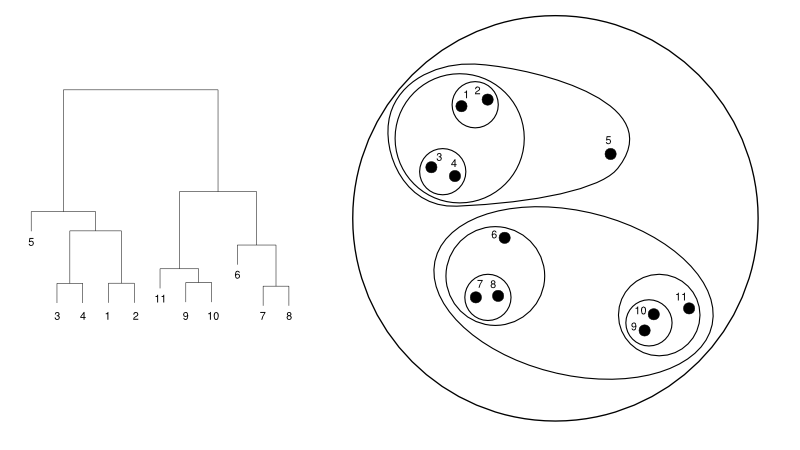
Источник

Здесь кластеризация может работать в любом случае, но результатом будет набор кластеров. Точки данных 1, 2, 3, 4, 5 и 6 сгруппированы по две одновременно. И формирование иерархии можно увидеть на левом рисунке, где показана дендрограмма того же самого. Тот же анализ поможет понять решение кластеров.

Определение количества кластеров

Одной из наиболее полезных функций этого алгоритма является то, что вы можете извлечь столько кластеров, сколько захотите, после завершения алгоритма. Он сильно отличается от алгоритма K-средних. В K-средних нам нужно передать гиперпараметр отсутствия кластеров. Это означает, что как только алгоритм завершит вычисления, у нас будет такое количество кластеров. Но если позже нам понадобится больше кластеров, мы не сможем так легко настроить. Единственным вариантом было бы изменить параметр и снова обучить модель.

Принимая во внимание, что когда дело доходит до иерархической кластеризации, вы можете установить количество кластеров позже. В конце можно взять два кластера. Если вас это не устраивает, вы можете взять пять кластеров, сформированных на предпоследнем или более высоком шаге. Это зависит от тебя. Следовательно, после обучения вам не нужно переобучать модель, чтобы получить больше или меньше кластеров. Этого можно добиться, просто обрезав дендрограмму на желаемом уровне.

Поскольку у нас есть концепции, давайте обсудим работу иерархической кластеризации в Python .

Для эксперимента мы собираемся использовать библиотеку обучения sci-kit для алгоритмов кластеризации. Мы также будем использовать модуль cluster.dendrogram из SciPy, чтобы визуализировать и понять процесс «разрезания» для ограничения количества кластеров.

импортировать numpy как np

X = np.массив([[3,5],

[12,9],

[13,17],

[14,14],

[60,52],

[55,63],

[69,59],])

На графике это выглядело бы примерно так:

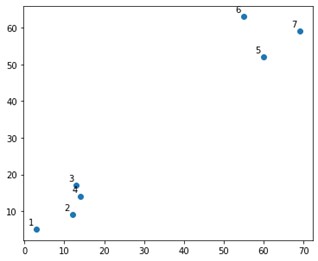
Что ж, мы видим, что у нас есть два окончательных кластера, в верхнем и нижнем углах. Давайте посмотрим, может ли алгоритм понять это или нет.

Мы будем использовать функцию AgglomerativeClustering из модуля sklearn.clustering.

из sklearn.cluster импортировать AgglomerativeClustering

кластер = AgglomerativeClustering (n_clusters = 2, affinity = 'евклидово', linkage = 'ward')

кластер.fit_predict(X)

Здесь мы указываем кластеры, что не является гиперпараметром. Однако мы просто передаем его, чтобы прояснить классы предсказания. Мы будем использовать функцию fit_predict для обучения, а также для прогнозирования классов по X.

Важно отметить, что агломеративная кластеризация используется чаще, чем разделительная, поскольку ее проще выполнить. Идея объединения кластеров на основе матриц близости кажется проще, чем разделение кластера на два с помощью какого-либо механизма.

Читайте: Scikit-learn в Python: особенности, предпосылки, плюсы и минусы

Чтобы четко понять, что произошло выше, посмотрите на шаги, включенные в алгоритм:

Работа алгоритма

Вот шаги для выполнения агломеративной кластеризации:

1. Определите каждую точку данных как кластер
2. Рассчитать начальную метрику близости
3. Объедините два кластера, которые являются «ближайшими» или похожими на основе метрики
4. Пересмотрите метрику близости и повторите третий шаг, пока не останется один кластер.

Итак, здесь остается только понять влияние различных методов близости. Как известно, в иерархической кластеризации в основном существует четыре типа методов близости. Это также известно как межкластерное сходство.

Методы (или связь, как определено в коде) включают:

1. МИН или одинарная связь
2. MAX или полная связь
3. Средняя связь
4. Центральная связь
5. Эксклюзивные функции целевых функций

Результаты того же можно легко визуализировать, применив параметр связи при создании дендрограмм.

Чтобы визуализировать вывод модели, нам просто нужен небольшой фрагмент кода:

plt.scatter(X[:,0],X[:,1], c=cluster.labels_, cmap='зима')

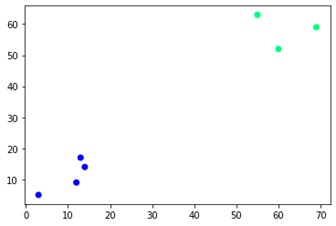
Как видите, в противоположных углах есть два разных кластера. Вы также можете поиграть с номерами кластеров и увидеть разные результаты. Всем этим можно управлять, вырезая дендрограммы. Чтобы понять это, давайте напишем небольшой фрагмент для визуализации создания дендрограмм.

Мы собираемся использовать функции дендрограммы и связи из модуля scipy.cluster.hierarchy. Здесь мы определяем связь, которую хотим использовать. Нам нужно передать этот объект функции дендрограммы для создания иерархии.

из scipy.cluster.hierarchy импортировать дендрограмму, связь

связанный = связь (X, 'полный')

список_меток = диапазон (1, 8)

plt.figure(figsize=(10, 7))

дендрограмма (связанная,

ориентация='сверху',

метки = список меток,

Distance_sort = 'по убыванию',

show_leaf_counts = Истина)

plt.show()

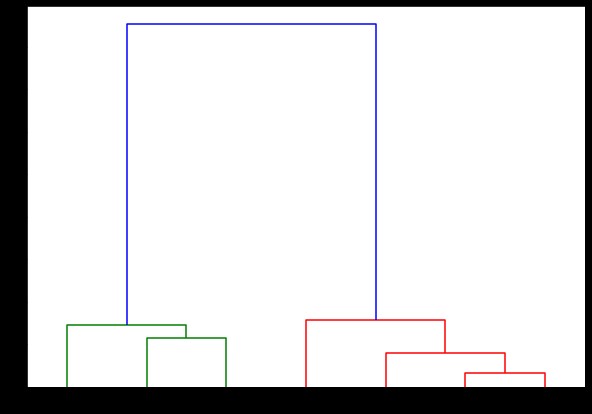
Здесь вы можете визуализировать, как формируются кластеры на каждой итерации. Таким образом, вы можете разрезать дендрограмму на любом уровне, и в итоге вы получите такое количество кластеров. Следовательно, из-за создания этой иерархии вы можете изменить количество кластеров после всего лишь одного запуска алгоритма и данных. Это то, что дает иерархической кластеризации преимущество перед другими алгоритмами, такими как K-средние.

Теперь давайте посмотрим, как использовать иерархическую кластеризацию в Python для часто используемого набора данных: IRIS . Мы будем читать набор данных из локального CSV. и просто взгляните на то, как выглядит набор данных и что нам нужно классифицировать.

импортировать numpy как np

импортировать панд как pd

импортировать matplotlib.pyplot как plt

%matplotlib встроенный

данные = pd.read_csv('радужная оболочка.csv')

данные.голова()

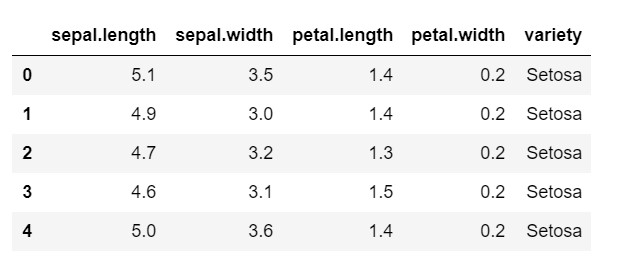
Как видите, целевой переменной является класс «разнообразие». Это строковый формат, который необходимо преобразовать в числа, так как для модели требуются закодированные метки. Для этого мы будем использовать кодировщик меток из библиотеки предварительной обработки sklearn. Простая подгонка и преобразование для преобразования их в числа.

предварительная обработка импорта из sklearn

le = предварительная обработка.LabelEncoder()

le.fit (данные ['разнообразие'])

данные ['разнообразие'] = le.transform (данные ['разнообразие'])

Теперь, если мы создадим на этом дендрограмму, мы найдем различные итерации и карты. Вот как это выглядит с одной связью. Если мы воспользуемся одним и тем же кодом и запустим его с полной или центроидальной связью, дендрограммы будут немного отличаться. Логика осталась прежней, но разные связи определенно повлияли бы на порядок слияния кластеров.

из scipy.cluster.hierarchy импортировать дендрограмму, связь

связанный = связь (данные, 'палата')

plt.figure(figsize=(10, 7))

дендрограмма (связанная)

plt.show()

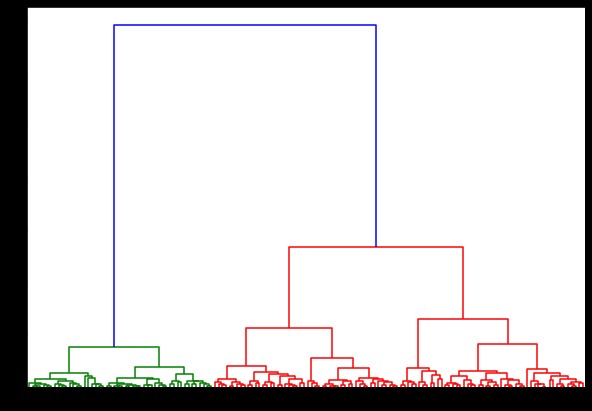
Теперь, применяя кластеризацию к набору данных, мы будем использовать две разные связи, и вы ясно увидите, какая разница на самом деле существует при определении кластеров. Как мы уже видели из кодировщика меток, у нас есть 3 разных класса, поэтому мы можем сначала применить 3 кластера.

из sklearn.cluster импортировать AgglomerativeClustering

cluster = AgglomerativeClustering (n_clusters = 3, affinity = 'евклидово', linkage = 'complete')

cluster.fit_predict(данные)

plt.figure(figsize=(10, 7))

plt.scatter(данные['sepal.length'], данные['petal.length'], c=cluster.labels_)

Как видно из рисунка выше, в 3-кластерной классификации связи показывают видимые изменения в предсказании. Сначала посмотрите на связь палаты. Он правильно предсказывает метки, сохраняя указанный выше кластер определенным, хотя в двух кластерах есть небольшая путаница значений. Но когда мы видим полную связь, она разрушает кластер и неправильно классифицирует некоторые значения.

Как мы знаем из методов близости, полная связь имеет тенденцию разрушать более крупные кластеры, как мы можем видеть выше. Метод подопечного или метод одиночной связи менее подвержен этим проблемам. Это было для простых наборов данных. Давайте посмотрим, как алгоритм страдает и на него влияют некоторые зашумленные наборы данных.

Одним из таких наборов данных является набор данных прогнозирования Pulsar или набор данных HTRU2 . Набор данных больше, так как он содержит около 18 000 образцов. Если смотреть с точки зрения ML, набор данных имеет довольно обычный размер или даже меньше. Но, сравнительно, он тяжелее, чем набор данных IRIS. Необходимость реализации на разнообразном наборе данных заключается в анализе производительности иерархической кластеризации в Python . Чтобы четко понимать способы и преимущества реализаций,

pulsar_data = pd.read_csv('pulsar_stars.csv')

pulsar_data.head()

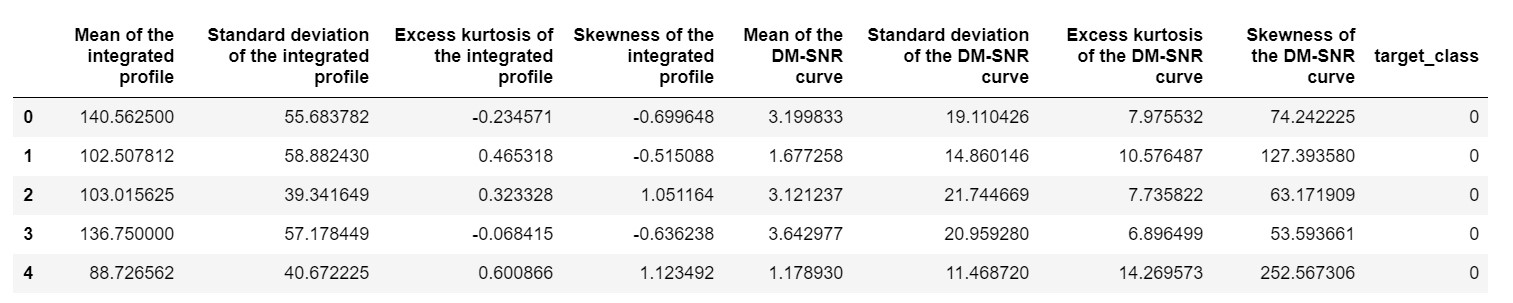
нам нужно будет нормализовать набор данных, чтобы он не был смещен из-за экстремальных значений.

нормализация импорта из sklearn.preprocessing

pulsar_data = нормализовать (pulsar_data)

Мы бы использовали стандартный код, но на этот раз мы синхронизируем оба вычисления.

%%время

из scipy.cluster.hierarchy импортировать дендрограмму, связь

связанный = связь (pulsar_data, 'палата')

plt.figure(figsize=(10, 7))

дендрограмма (связанная)

plt.show()

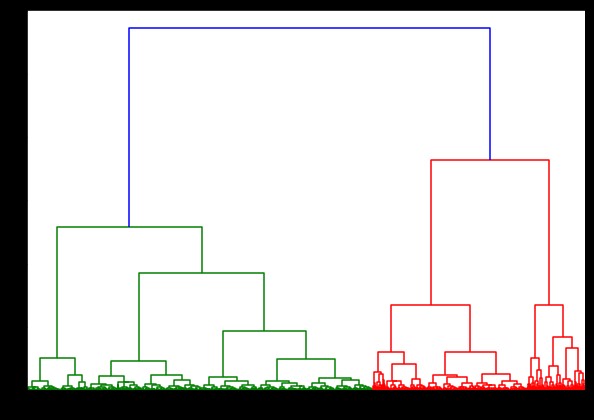
Время создания дендрограммы в наборе данных IRIS составило 6 секунд. Время создания дендрограммы для набора данных HTRU2 составило 13 минут 54 секунды. Но это ничто по сравнению с изменением прогнозов из-за различных связей, которое вы наблюдаете в модели, обученной с набором данных HTRU2.

Проделаем ту же процедуру, что и раньше. На этот раз мы будем делать прогнозы для каждой связи.

На следующем рисунке показаны прогнозы кластеризации для каждой связи:

cluster = AgglomerativeClustering(n_clusters=2, affinity='euclidean', linkage='average') #а также полные, палатные и одиночные

cluster.fit_predict(pulsar_data)

plt.figure(figsize=(10, 7))

plt.scatter(pulsar_data[:,1], pulsar_data[:,7], c=cluster.labels_)

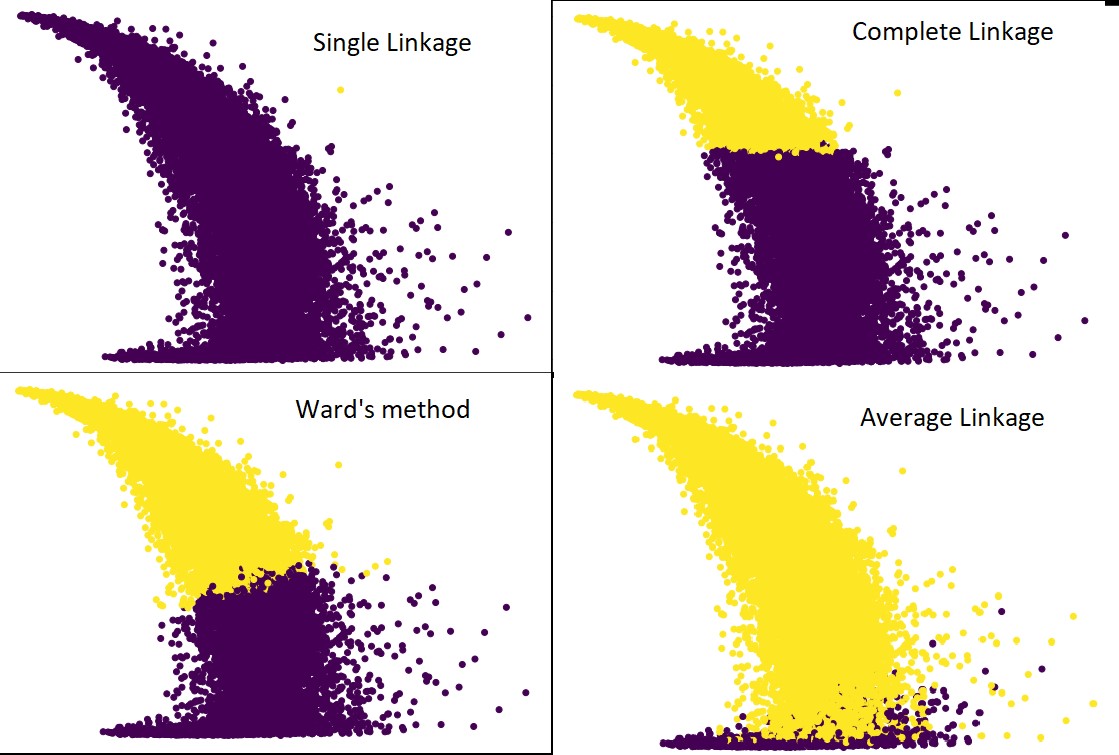
Да, действительно удивительно, насколько предсказания отличаются друг от друга. Это показывает важность матрицы близости в иерархической кластеризации.

Как видите, одинарная связь охватывает почти все точки, поскольку минимальное расстояние между двумя кластерами определяет метрику близости. Это делает его уязвимым для зашумленных данных. Если мы увидим полное связывание, оно определенно разделит данные на два кластера, но, возможно, разобьет большой кластер только из-за его близости.

Средняя связь — это компромисс между ними. На него меньше влияет шум, но он все же может разбивать большие кластеры, но с меньшей вероятностью. И он лучше справляется с классификацией.

Целевые функции, такие как метод варда, иногда используются для инициализации других методов кластеризации, таких как K-средних. Этот метод, как и метод средней связи, имеет компромисс между методами одиночной и полной связи. Целевые функции, такие как метод Уорда, в основном используются в индивидуальных решениях, чтобы уменьшить вероятность неправильной классификации. И мы видим, что он работает хорошо.

Изучите: Кластерный анализ в интеллектуальном анализе данных: приложения, методы и требования

Сложность времени и пространства

Просто для понимания рассмотрим способ определения и расчета метрики близости. Метрика близости требует сохранения расстояния между каждой парой кластеров внутри карты данных. Это делает космическую сложность: O (n2). Это большое число. Для сравнения, представьте, что у нас есть 1 000 000 баллов. Это увеличит требования к пространству до 1012 баллов. Взяв грубое среднее значение, приблизив размер одной точки к байту, мы получим размер данных в 1 ТБ. И это нужно хранить в оперативной памяти, а не на жестком диске.

Во-вторых, временная сложность. Из-за необходимости сканирования матрицы близости на каждой итерации и учитывая, что мы делаем n шагов, мы получаем сложность как O (n3). Это требует больших вычислительных ресурсов, особенно для больших наборов данных.

Возможно, его можно снизить до O(n2logn), но это все равно слишком дорого по сравнению с другими алгоритмами кластеризации, такими как K-средних. Если вы хотите узнать больше об анализе пространственной и временной сложности алгоритмов и оптимизации функций стоимости, вы можете перейти к программам upGrad по науке о данных и машинному обучению.

Ограничения

• Мы уже обсуждали первое ограничение: пространственную и временную сложность. Очевидно, что иерархическая кластеризация не подходит для больших наборов данных. Даже если временная сложность управляется более быстрыми вычислительными машинами, пространственная сложность слишком высока. Особенно, когда мы загружаем его в оперативную память. И проблема скорости становится еще больше, когда мы реализуем иерархическую кластеризацию в Python. Python медленный, и если речь идет о больших задачах, он обязательно пострадает.
• Во-вторых, нет оптимизированной техники с близостью. Если мы видим, что у каждого есть несколько проблем и ограничений, это делает внутренний механизм алгоритма неоптимизированным.
• Когда мы смотрим на решения по кластеризации, они не подлежат отмене. Это означает, что после того, как кластеризация была применена для определенной итерации, она не будет изменяться в дальнейших итерациях до завершения. Таким образом, если из-за структурных неточностей алгоритм в любой момент выбирает неправильные кластеры для объединения или разделения, это необратимо.
• Если мы внимательно посмотрим на алгоритм, у нас нет четкой целевой функции, которая минимизируется. В других алгоритмах есть определенная функция, которую мы пытаемся оптимизировать. Например, в K-средних у нас есть четкая функция стоимости, которую мы минимизируем, чего нельзя сказать о иерархической кластеризации.

Проверьте: 9 лучших алгоритмов науки о данных, которые должен знать каждый специалист по данным

Заключение

Несмотря на определенные ограничения, когда речь идет о больших наборах данных, этот тип алгоритма кластеризации привлекателен при работе с наборами данных малого и среднего масштаба. Алгоритм иерархической кластеризации в Python не получил большого развития в архитектуре или схеме из-за его тревожной потребности во временной и пространственной сложности.

И это правда, что сейчас время больших данных. Это означает, что нам нужны алгоритмы, которые лучше масштабируются. Но, тем не менее, в тех случаях, когда мы не уверены в количестве кластеров или нам нужно эффективно уточнить анализ, иерархическая кластеризация в Python может быть удовлетворительным выбором.

Теперь вы знаете, как реализовать иерархическую кластеризацию в Python.

Чтобы лучше понять такие алгоритмы и приложения методов в машинном обучении и науке о данных, ознакомьтесь с курсами, предлагаемыми upGrad. У нас есть накопительные программы для любого карьерного пути, которым вы хотите следовать.

Программы курируются ведущими профессионалами, а также профессорами IIIT-B. Для получения дополнительной информации отправляйтесь на сайт upGrad . Если вам интересно изучать науку о данных, чтобы быть в авангарде быстро развивающихся технологий, ознакомьтесь с программой Executive PG upGrad & IIIT-B по науке о данных.