Klastrowanie hierarchiczne w Pythonie [koncepcje i analiza]

Wraz ze wzrostem przepływu surowych danych i potrzebą analizy, koncepcja uczenia się bez nadzoru stała się z czasem popularna. Służy do wyciągania wniosków z zestawów danych składających się z danych wejściowych bez oznaczonych wartości docelowych. Zanim zaczniemy omawiać hierarchiczne klastrowanie w Pythonie i stosować algorytm na różnych zestawach danych, przyjrzyjmy się podstawowej idei klastrowania.

Klastrowanie zajmuje się głównie klasyfikacją danych surowych. Obejmuje grupowanie różnych punktów danych, które są do siebie najbardziej podobne. Grupy te nazywane są klastrami, które są tworzone na podstawie zdefiniowanej metryki podobieństwa lub klastrowania.

Wstęp

Klastrowanie hierarchiczne zajmuje się danymi w formie drzewa lub dobrze zdefiniowanej hierarchii. Proces ten polega na zajmowaniu się jednocześnie dwoma klastrami. Przy podejmowaniu decyzji obliczeniowych algorytm opiera się na macierzy podobieństwa lub odległości. Znaczenie, które dwa klastry połączyć lub jak podzielić klaster na dwa. Mając na uwadze te dwie opcje, mamy dwa rodzaje klastrowania hierarchicznego . Jeśli jesteś początkującym i chcesz dowiedzieć się więcej na temat nauki o danych, sprawdź nasze kursy nauki o danych prowadzone przez najlepsze uniwersytety.

Jednym z krytycznych aspektów algorytmu jest macierz podobieństwa (nazywana również macierzą bliskości), na której przebiega cały algorytm. Istnieje wiele metod zbliżeniowych, które omówiono w dalszej części artykułu.

Rodzaje

Klastrowanie hierarchiczne ma dwa typy:

1. Grupowanie aglomeracyjne
2. Grupowanie dzielące

Typy są zgodne z podstawową funkcjonalnością: sposobem tworzenia hierarchii. Aglomeracja to generator hierarchii oddolnej, podczas gdy dzielna to generator hierarchii odgórnej.

Aglomeracja przyjmuje wszystkie punkty jako indywidualne klastry, a następnie łączy je w każdej iteracji, po dwa naraz. Dzielenie rozpoczyna się od przyjęcia wszystkich danych jako jednego skupienia i dzieli je, aż wszystkie punkty staną się indywidualnymi skupieniami.

Rezultatem jest zestaw zagnieżdżonych klastrów, które można postrzegać jako drzewo hierarchiczne. Najlepszym sposobem, aby to zobaczyć, jest przekształcenie struktury zbioru w dendrogram, aby wyświetlić hierarchię.

Poniżej przedstawiono prosty przykład dendrogramu w porównaniu z reprezentacją skupień:

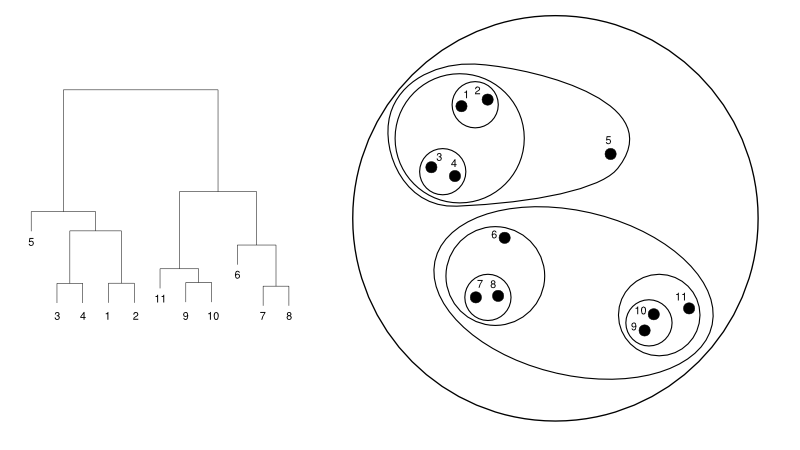
Źródło

W tym przypadku klastrowanie może działać w obie strony, ale wynikiem będzie zbiór klastrów. Punkty danych 1, 2, 3, 4, 5 i 6 są zgrupowane w dwóch jednocześnie. A ułożenie hierarchii widać na lewym rysunku, który dotyczy dendrogramu tego samego. Ta sama analiza pomogłaby w zrozumieniu decyzji klastrów.

Decydowanie o liczbie klastrów

Jedną z najbardziej przydatnych funkcji tego algorytmu jest możliwość wyodrębnienia dowolnej liczby klastrów po zakończeniu działania algorytmu. Jest zupełnie inny niż algorytm K-średnich. W K-średnich musimy przekazać hiperparametr bez skupień. Oznacza to, że gdy algorytm zakończy obliczenia, będziemy mieli tyle klastrów. Ale jeśli później potrzebujemy więcej klastrów, nie możemy tak łatwo dostroić. Jedyną opcją byłaby zmiana parametru i ponowne trenowanie modelu.

Natomiast jeśli chodzi o klastrowanie hierarchiczne, liczbę klastrów można ustawić później. Na końcu możesz wziąć dwa klastry. Jeśli nie jesteś usatysfakcjonowany, możesz wziąć pięć klastrów utworzonych na przedostatnim lub wyższym stopniu. To zależy od Ciebie. Dlatego po przeszkoleniu nie trzeba ponownie trenować modelu, aby uzyskać więcej lub mniej klastrów. Można to osiągnąć, po prostu przycinając dendrogram do pożądanego poziomu.

Skoro już omówiliśmy koncepcje, omówmy działanie hierarchicznego klastrowania w Pythonie .

Do eksperymentu użyjemy biblioteki sci-kit do uczenia algorytmów klastrowania. Wykorzystalibyśmy również moduł cluster.dendrogram z SciPy, aby zwizualizować i zrozumieć proces „cięcia” w celu ograniczenia liczby klastrów.

importuj numer jako np

X = np. tablica ([[3,5],

[12,9],

[13,17],

[14,14],

[60,52],

[55,63],

[69,59],])

Na fabule wyglądałoby to mniej więcej tak:

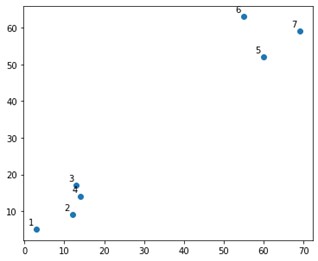
Cóż, widzimy, że mamy dwie definitywne gromady, w górnym i dolnym rogu. Zobaczmy, czy algorytm może to rozgryźć, czy nie.

Korzystalibyśmy z funkcji AgglomerativeClustering z modułu sklearn.clustering.

od sklearn.cluster import AglomerativeClustering

klaster = AglomerativeClustering(n_clusters=2, affinity='euklidesowy', linkage='ward')

klaster.fit_predict(X)

Tutaj określamy klastry, co nie jest hiperparametrem. Jednak po prostu przekazujemy go, aby klasy przewidywania były jasne. Użylibyśmy funkcji fit_predict do trenowania oraz przewidywania klas przez X.

Należy zauważyć, że klaster aglomeracyjny jest bardziej używany niż podział, ponieważ jest prostszy do wykonania. Pomysł łączenia klastrów opartych na macierzach zbliżeniowych wydaje się prostszy niż dzielenie klastra na dwa za pomocą jakiegoś mechanizmu.

Przeczytaj: Nauka Scikit w Pythonie: funkcje, wymagania wstępne, zalety i wady

Aby jasno zrozumieć, co się stało powyżej, spójrz na kroki związane z algorytmem:

Działanie algorytmu

Oto kroki, aby wykonać grupowanie aglomeracyjne:

1. Zdefiniuj każdy punkt danych jako klaster
2. Oblicz początkową metrykę bliskości
3. Połącz dwa klastry, które są „najbliższe” lub podobne na podstawie metryki
4. Popraw metrykę bliskości i powtórz trzeci krok, aż pozostanie pojedynczy klaster.

Tak więc jedyne, co pozostaje do zrozumienia, to wpływ różnych metod zbliżeniowych. Jak wiadomo, w hierarchicznym grupowaniu istnieją cztery rodzaje metod zbliżeniowych. Jest to również znane jako podobieństwo między klastrami.

Metody (lub powiązanie, zgodnie z definicją w kodzie) obejmują:

1. MIN lub Pojedynczy podnośnik
2. Połączenie MAX lub pełne
3. Średnie połączenie
4. Połączenie centroid
5. Wyłączne funkcje funkcji obiektywnych

Wyniki tego samego można łatwo zwizualizować, stosując opcję łączenia podczas tworzenia dendrogramów.

Aby zwizualizować dane wyjściowe modelu, potrzebujemy tylko małego fragmentu kodu w następujący sposób:

plt.scatter(X[:,0],X[:,1], c=cluster.labels_, cmap='zima')

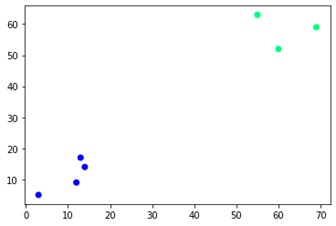
Jak widać, na przeciwległych rogach znajdują się dwa różne skupiska. Równie dobrze możesz pobawić się liczbami klastrów i zobaczyć różne wyniki. Całość można napędzać wycinaniem dendrogramów. Aby to zrozumieć, napiszmy mały fragment do wizualizacji tworzenia dendrogramów.

Będziemy korzystać z funkcji dendrogramu i linkage z modułu scipy.cluster.hierarchy. Tutaj definiujemy powiązanie, którego chcemy użyć. Musimy przekazać ten obiekt do funkcji dendrogramu, aby wygenerować hierarchię.

ze scipy.cluster.hierarchy importuj dendrogram, powiązanie

linked = linkage(X, 'kompletne')

lista_etykiet = zakres(1, 8)

plt.figure(figsize=(10, 7))

dendrogram(połączony,

orientacja='góra',

etykiety=ListaEtykiet,

sortowanie_odległości='malejąco',

show_leaf_counts=Prawda)

plt.pokaż()

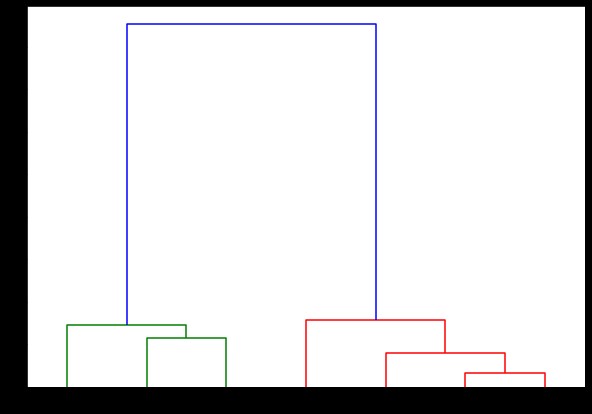
Tutaj możesz zwizualizować sposób tworzenia klastrów w każdej iteracji. Możesz więc wyciąć dendrogram na dowolnym poziomie, a skończysz z taką liczbą skupisk. W związku z tym, ze względu na tworzenie hierarchii, możesz zmienić liczbę klastrów już po jednym przejściu przez algorytm i dane. To właśnie daje hierarchicznemu klastrowaniu przewagę nad innymi algorytmami, takimi jak K-średnie.

Przyjrzyjmy się teraz, jak używać hierarchicznego klastrowania w Pythonie na powszechnie używanym zbiorze danych: IRIS . Czytamy zbiór danych z lokalnego pliku csv. i po prostu rzucić okiem na to, jak wygląda zbiór danych i co musimy sklasyfikować.

importuj numer jako np

importuj pandy jako PD

importuj matplotlib.pyplot jako plt

%matplotlib wbudowany

dane = pd.read_csv('iris.csv')

data.head()

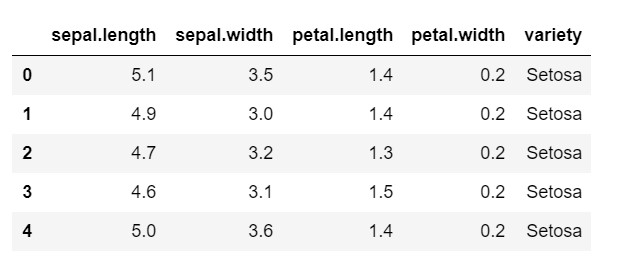
Jak widać, zmienną docelową jest klasa 'variety'. Jest to ciąg znaków, który należy przekonwertować na liczby, ponieważ model wymaga zakodowanych etykiet. Aby to zrobić, użyjemy kodera etykiet z biblioteki przetwarzania wstępnego sklearna. Proste dopasowanie i przekształcenie w celu przekształcenia ich w liczby.

z wstępnego przetwarzania importu sklearn

le = przetwarzanie wstępne.LabelEncoder()

le.fit(dane['odmiana'])

dane['odmiana'] = le.transform(dane['odmiana'])

Teraz, jeśli stworzymy na tym dendrogram, znajdziemy różne iteracje i mapy. Tak to wygląda z jednym sprzęgłem. Jeśli użyjemy tego samego kodu i uruchomimy go z pełnym lub centroidalnym połączeniem, dendrogramy będą się nieco różnić. Logika pozostaje taka sama, ale różne powiązania zdecydowanie wpłynęłyby na kolejność łączenia klastrów.

ze scipy.cluster.hierarchy importuj dendrogram, powiązanie

linked = linkage(dane, 'oddział')

plt.figure(figsize=(10, 7))

dendrogram(połączony)

plt.pokaż()

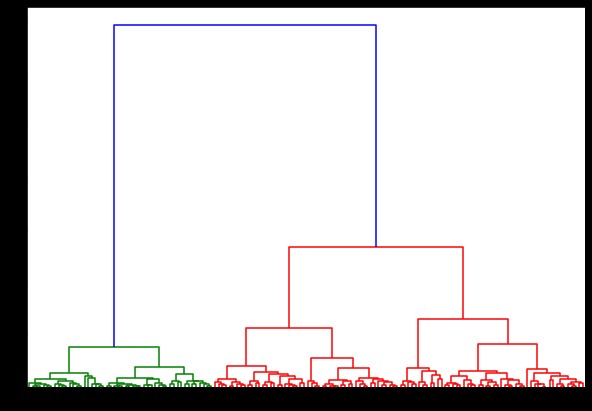
Teraz, stosując klastrowanie w zestawie danych, użyjemy dwóch różnych powiązań i wyraźnie zobaczysz, jaka naprawdę ma różnica podczas definiowania klastrów. Jak już widzieliśmy z kodera etykiet, mamy 3 różne klasy, więc na początku możemy zastosować 3 klastry.

od sklearn.cluster import AglomerativeClustering

klaster = AglomerativeClustering(n_clusters=3, powinowactwo='euklidesowe', powiązanie='kompletne')

klaster.fit_predict(dane)

plt.figure(figsize=(10, 7))

plt.scatter(dane['sepal.length'], dane['petal.length'], c=cluster.labels_)

Jak widać na powyższym rysunku, w klasyfikacji 3-klastrowej powiązania pokazują widoczne zmiany w przewidywaniu. Najpierw spójrz na połączenie oddziału. Prawidłowo przewiduje etykiety, utrzymując powyższy klaster zdefiniowany, mimo że w dwóch klastrach występuje niewielka mieszanka wartości. Ale kiedy widzimy pełne powiązanie, rozbija klaster i błędnie klasyfikuje niektóre wartości.

Jak wiemy w metodach zbliżeniowych, pełne powiązanie ma tendencję do łamania większych klastrów, jak widać powyżej. Metoda oddziału lub metoda pojedynczego połączenia jest mniej podatna na te problemy. Dotyczyło to prostych zestawów danych. Zobaczmy, jak algorytm cierpi i jest dotknięty niektórymi zaszumionymi zestawami danych.

Jednym z takich zestawów danych jest zestaw danych przewidywania Pulsar lub zestaw danych HTRU2 . Zbiór danych jest większy, ponieważ zawiera około 18 000 próbek. Zestaw danych widziany z perspektywy ML ma dość regularny rozmiar, a nawet mniejszy. Ale porównywalnie jest cięższy niż zbiór danych IRIS. Potrzeba implementacji na zróżnicowanym zbiorze danych polega na analizie wydajności hierarchicznego grupowania w Pythonie . Aby jasno zrozumieć sposoby i zalety wdrożeń,

pulsar_data = pd.read_csv('pulsar_stars.csv')

pulsar_data.head()

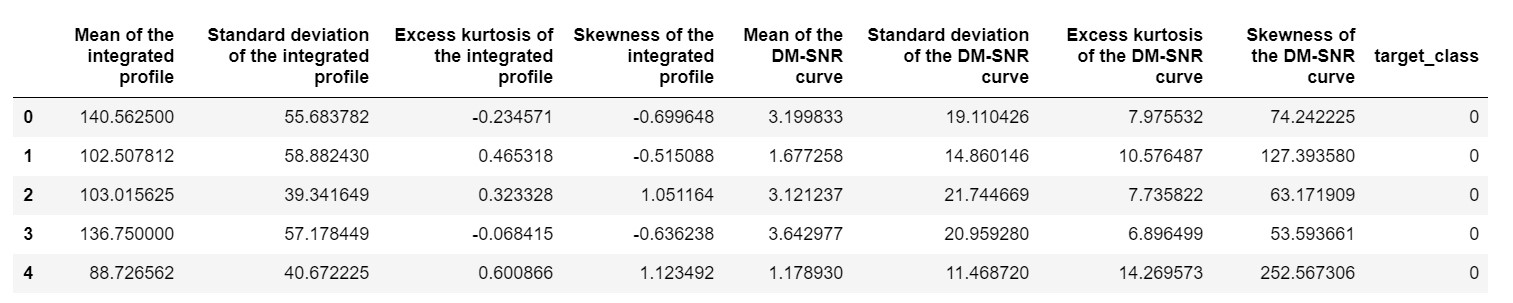
musielibyśmy znormalizować zbiór danych, aby nie był stronniczy z powodu ekstremalnych wartości.

ze sklearn.preprocessing import normalize

pulsar_data = normalizuj(pulsar_data)

Używalibyśmy standardowego kodu, ale tym razem synchronizujemy oba obliczenia.

%%czas

ze scipy.cluster.hierarchy importuj dendrogram, powiązanie

linked = linkage(pulsar_data, 'ward')

plt.figure(figsize=(10, 7))

dendrogram(połączony)

plt.pokaż()

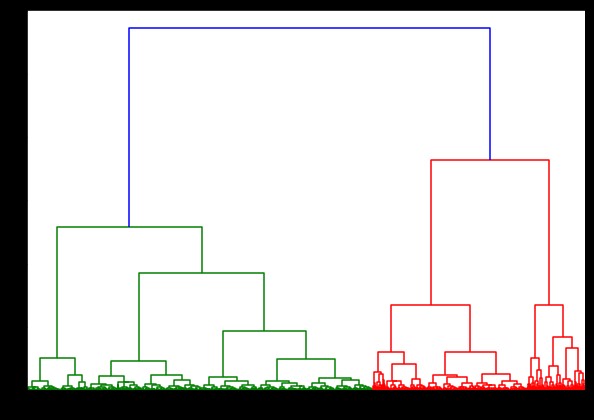
Czas wygenerowania dendrogramu w zbiorze danych IRIS wynosił 6 sekund. Czas generowania dendrogramu na zestawie danych HTRU2 wynosił 13 min 54 sekundy. Ale to nic w porównaniu ze zmianą przewidywań z powodu różnych powiązań, którą obserwujesz w modelu wytrenowanym za pomocą zestawu danych HTRU2.

Prześledźmy tę samą procedurę, co przedtem. Tym razem przewidywaliśmy każdy związek.

Poniższy rysunek przedstawia przewidywania klastrowania z każdym powiązaniem:

cluster = AglomerativeClustering(n_clusters=2, affinity='euclidean', linkage='average') #a także kompletne, odległe i pojedyncze

cluster.fit_predict(pulsar_data)

plt.figure(figsize=(10, 7))

plt.scatter(pulsar_data[:,1], pulsar_data[:,7], c=cluster.labels_)

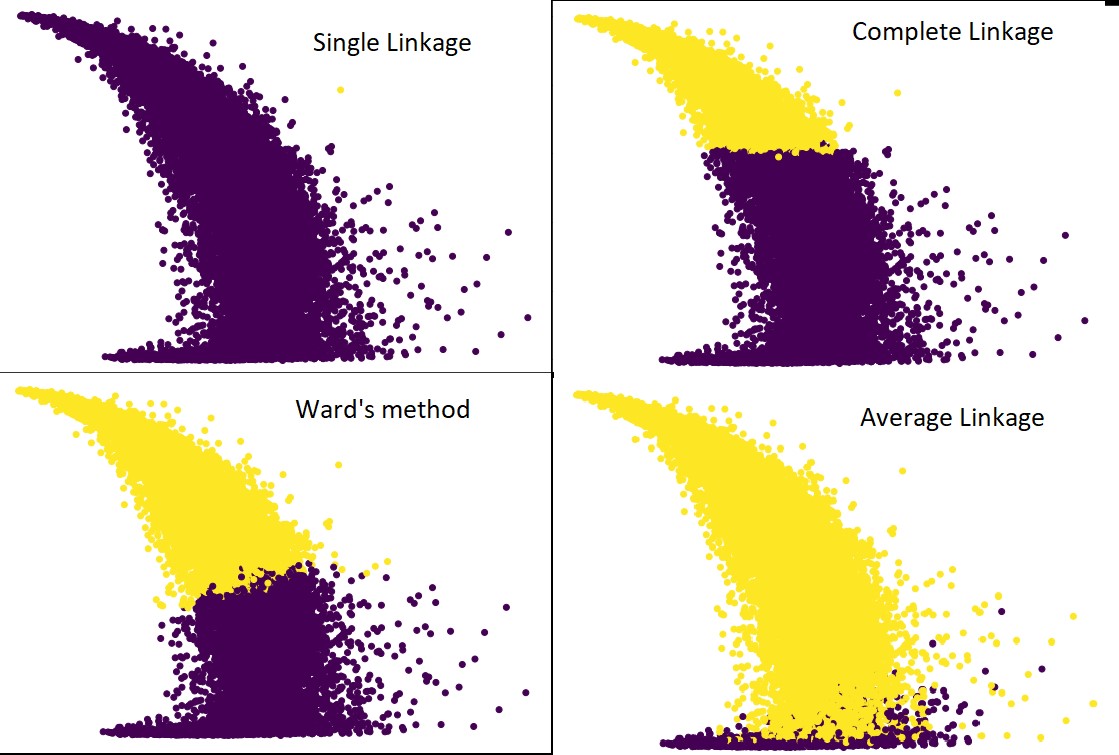
Tak, to rzeczywiście zaskakujące, jak bardzo te prognozy różnią się od siebie. Pokazuje to znaczenie macierzy bliskości w hierarchicznym grupowaniu.

Jak widać, pojedyncze powiązanie zajmuje prawie wszystkie punkty, ponieważ minimalna odległość między dwoma skupieniami określa metrykę bliskości. To sprawia, że ​​jest podatny na zaszumione dane. Jeśli zobaczymy pełne powiązanie, to zdecydowanie dzieli dane na dwie gromady, ale mogło to spowodować uszkodzenie dużej gromady tylko ze względu na jej bliskość.

Średnie powiązanie jest kompromisem między nimi. Jest mniej podatny na hałas, ale nadal może rozbijać duże gromady, ale z mniejszym prawdopodobieństwem. I lepiej radzi sobie z klasyfikacją.

Funkcje celu, takie jak metoda warda, są czasami używane do inicjowania innych metod grupowania, takich jak K-średnie. Ta metoda, podobnie jak wiązanie średnie, ma kompromis między metodą pojedynczego i pełnego wiązania. Funkcje obiektywne, takie jak metoda oddziału, są wykorzystywane głównie w niestandardowych rozwiązaniach, aby zmniejszyć prawdopodobieństwo błędnej klasyfikacji. I widzimy, że działa dobrze.

Dowiedz się: Analiza klastrów w eksploracji danych: aplikacje, metody i wymagania

Złożoność czasu i przestrzeni

Aby to zrozumieć, rozważ sposób definiowania i obliczania metryki bliskości. Metryka bliskości wymaga przechowywania odległości między każdą parą klastrów na mapie danych. Daje to złożoność przestrzeni: O(n2). To duża liczba. Aby spojrzeć na to z innej perspektywy, wyobraź sobie, że mamy 1 000 000 punktów. To podniesie wymagania dotyczące miejsca do 1012 punktów. Przyjmując przybliżoną i ciężką średnią, przybliżając rozmiar jednego punktu jako bajt, otrzymujemy rozmiar danych wynoszący 1 TB. A to musi być przechowywane w pamięci RAM, a nie na dysku twardym.

Po drugie, pojawia się złożoność czasu. Na potrzeby skanowania macierzy zbliżeniowej w każdej iteracji i biorąc pod uwagę, że wykonujemy n kroków, otrzymujemy złożoność O(n3). Jest to kosztowne obliczeniowo, zwłaszcza w przypadku dużych zbiorów danych.

Możliwe jest sprowadzenie go do O(n2logn), ale nadal jest zbyt drogi w porównaniu z innymi algorytmami klastrowania, takimi jak K-średnie. Jeśli chcesz dowiedzieć się więcej na temat analizowania złożoności przestrzennej i czasowej algorytmów oraz optymalizacji funkcji kosztów, możesz udać się do uaktualnionych programów w dziedzinie nauki o danych i uczenia maszynowego.

Ograniczenia

• Omówiliśmy już pierwsze ograniczenie: złożoność przestrzeni i czasu. Oczywiste jest, że klastrowanie hierarchiczne nie jest korzystne w przypadku dużych zbiorów danych. Nawet jeśli złożoność czasowa jest zarządzana za pomocą szybszych maszyn obliczeniowych, złożoność kosmiczna jest zbyt wysoka. Zwłaszcza, gdy ładujemy go do pamięci RAM. A kwestia szybkości wzrasta jeszcze bardziej, gdy wdrażamy hierarchiczne grupowanie w Pythonie. Python jest powolny i jeśli chodzi o duże zadania, na pewno ucierpi.
• Po drugie, nie ma zoptymalizowanej techniki bliskości. Jeśli zauważymy, że każdy z nich ma wiele problemów i ograniczeń, powoduje to niezoptymalizowanie wewnętrznego mechanizmu algorytmu.
• Kiedy przyjrzymy się decyzjom dotyczącym grupowania, nie da się ich wycofać. Oznacza to, że po zastosowaniu klastrowania do określonej iteracji nie będzie on zmieniany w kolejnych iteracjach aż do zakończenia. Tak więc, jeśli z powodu niedokładności strukturalnych algorytm w dowolnym momencie wybierze niewłaściwe klastry do połączenia lub podziału, jest to nieodwołalne.
• Jeśli przyjrzymy się bliżej algorytmowi, nie mamy wyraźnej funkcji celu, która jest minimalizowana. W innych algorytmach istnieje określona funkcja, którą staramy się zoptymalizować. Na przykład w K-means mamy wyraźną funkcję kosztu, którą minimalizujemy, co nie ma miejsca w przypadku grupowania hierarchicznego.

Sprawdź: 9 najlepszych algorytmów analizy danych, które każdy naukowiec powinien znać

Wniosek

Chociaż istnieją pewne ograniczenia, jeśli chodzi o duże zestawy danych, ten rodzaj algorytmu grupowania jest atrakcyjny w przypadku zestawów danych o małej i średniej skali. Algorytm hierarchicznego grupowania w Pythonie nie rozwinął się zbytnio w architekturze lub schemacie ze względu na jego alarmującą potrzebę złożoności czasowej i przestrzennej.

I to prawda, że ​​teraz nadszedł czas Big Data. Oznacza to, że potrzebujemy algorytmów, które lepiej się skalują. Jednak nadal w przypadkach, gdy nie jesteśmy pewni liczby klastrów lub musimy skutecznie udoskonalić analizę, klastrowanie hierarchiczne w Pythonie może być zadowalającym wyborem.

Dzięki temu wiesz już, jak zaimplementować klastrowanie hierarchiczne w Pythonie.

Aby zrozumieć więcej takich algorytmów i zastosowań metod w uczeniu maszynowym i nauce o danych, zapoznaj się z ofertą kursów upGrad. Mamy programy kumulacyjne dla dowolnej ścieżki kariery, którą chcesz podążać.

Kuratorami programów są najlepsi specjaliści, a także profesorowie IIIT-B. Aby uzyskać więcej informacji, przejdź do upGrad . Jeśli jesteś ciekawy, jak uczyć się nauki o danych, aby być na czele szybkiego postępu technologicznego, sprawdź program Executive PG w dziedzinie nauki o danych.