Hierarchisches Clustering in Python [Konzepte und Analyse]

Mit der Zunahme des Flusses von Rohdaten und dem Bedarf an Analysen wurde das Konzept des unüberwachten Lernens im Laufe der Zeit populär. Es wird verwendet, um Erkenntnisse aus Datensätzen zu ziehen, die aus Eingabedaten ohne gekennzeichnete Zielwerte bestehen. Bevor wir damit beginnen, das hierarchische Clustering in Python zu diskutieren und den Algorithmus auf verschiedene Datensätze anzuwenden, lassen Sie uns noch einmal auf die Grundidee des Clustering zurückkommen.

Beim Clustering geht es hauptsächlich um die Klassifizierung von Rohdaten. Es besteht darin, verschiedene Datenpunkte zusammenzufassen, die einander am ähnlichsten sind. Diese Gruppen werden Cluster genannt, die basierend auf der definierten Ähnlichkeits- oder Clustering-Metrik gebildet werden.

Einführung

Hierarchisches Clustering befasst sich mit Daten in Form eines Baums oder einer wohldefinierten Hierarchie. Der Prozess umfasst den Umgang mit zwei Clustern gleichzeitig. Der Algorithmus stützt sich auf eine Ähnlichkeits- oder Distanzmatrix für Berechnungsentscheidungen. Das heißt, welche zwei Cluster zusammengeführt werden sollen oder wie ein Cluster in zwei geteilt werden soll. Unter Berücksichtigung dieser beiden Optionen haben wir zwei Arten von hierarchischem Clustering . Wenn Sie Anfänger sind und mehr über Data Science erfahren möchten, sehen Sie sich unsere Data Science-Kurse von Top-Universitäten an.

Einer der kritischen Aspekte des Algorithmus ist die Ähnlichkeitsmatrix (auch bekannt als Proximity-Matrix), da der gesamte Algorithmus auf ihrer Grundlage vorgeht. Es gibt viele Näherungsmethoden, die weiter unten in diesem Artikel besprochen werden.

Typen

Es gibt zwei Arten von hierarchischem Clustering:

1. Agglomerative Clusterbildung
2. Trennendes Clustering

Die Typen entsprechen der grundlegenden Funktionalität: der Art und Weise, Hierarchien zu entwickeln. Agglomerativ ist ein Bottom-Up-Hierarchiegenerator, während Divisiv ein Top-Down-Hierarchiegenerator ist.

Agglomerativ nimmt alle Punkte als einzelne Cluster und führt sie dann bei jeder Iteration zusammen, jeweils zwei auf einmal. Divisive beginnt damit, dass die gesamten Daten als ein Cluster angenommen und geteilt werden, bis alle Punkte zu einzelnen Clustern werden.

Das Ergebnis ist eine Reihe verschachtelter Cluster, die als hierarchischer Baum wahrgenommen werden können. Der beste Weg, es anzuzeigen, besteht darin, die Mengenstruktur in ein Dendrogramm umzuwandeln, um die Hierarchie anzuzeigen.

Im Folgenden finden Sie ein einfaches Beispiel für ein Dendrogramm im Vergleich zur Clusterdarstellung:

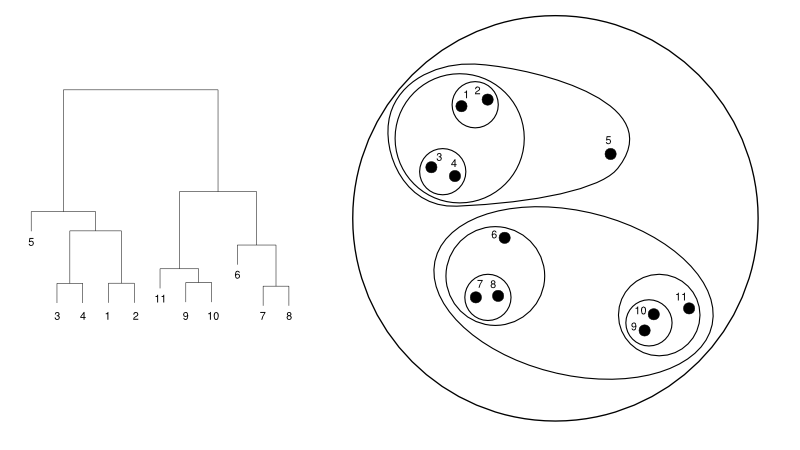
Quelle

Hier kann das Clustering in beide Richtungen funktionieren, aber das Ergebnis wird eine Sammlung von Clustern sein. Die Datenpunkte 1, 2, 3, 4, 5 und 6 werden jeweils in zwei gruppiert. Und die Hierarchiebildung ist in der linken Abbildung zu sehen, die sich mit dem Dendrogramm derselben befasst. Dieselbe Analyse würde helfen, die Entscheidung von Clustern zu verstehen.

Die Anzahl der Cluster bestimmen

Eines der nützlichsten Merkmale dieses Algorithmus ist, dass Sie so viele Cluster extrahieren können, wie Sie möchten, sobald der Algorithmus beendet ist. Es unterscheidet sich stark vom K-Means-Algorithmus. In K-Means müssen wir den No-of-Clusters-Hyperparameter übergeben. Das bedeutet, dass wir so viele Cluster haben würden, sobald der Algorithmus die Berechnung abgeschlossen hat. Aber wenn wir später mehr Cluster brauchen, können wir das nicht so einfach tunen. Die einzige Möglichkeit wäre, den Parameter zu ändern und das Modell erneut zu trainieren.

Beim hierarchischen Clustering hingegen können Sie die Anzahl der Cluster später festlegen. Sie können am Ende zwei Cluster nehmen. Wenn Sie nicht zufrieden sind, können Sie die fünf Cluster nehmen, die im vorletzten oder höheren Schritt gebildet wurden. Es hängt von dir ab. Daher müssen Sie das Modell nach dem Training nicht erneut trainieren, um mehr oder weniger Cluster zu erhalten. Dies kann erreicht werden, indem Sie einfach das Dendrogramm auf der gewünschten Ebene schneiden .

Nachdem wir die Konzepte festgelegt haben, wollen wir die Funktionsweise von hierarchischem Clustering in Python besprechen .

Für das Experiment werden wir die Lernbibliothek von sci-kit für die Clustering-Algorithmen verwenden. Wir würden auch das cluster.dendrogram-Modul von SciPy verwenden, um den „Cutting“-Prozess zur Begrenzung der Anzahl von Clustern zu visualisieren und zu verstehen.

importiere numpy als np

X = np.array([[3,5],

[12,9],

[13,17],

[14,14],

[60,52],

[55,63],

[69,59],])

Auf einem Plot würde das etwa so aussehen:

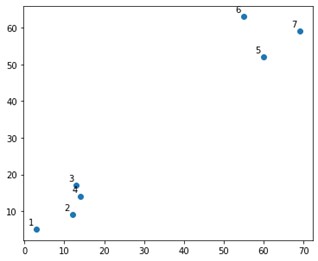
Nun, wir sehen, dass wir zwei definitive Cluster haben, an der oberen und unteren Ecke. Mal sehen, ob der Algorithmus es herausfinden kann oder nicht.

Wir würden die AgglomerativeClustering-Funktion aus dem sklearn.clustering-Modul verwenden.

aus sklearn.cluster import AgglomerativeClustering

cluster = AgglomerativeClustering(n_clusters=2, affinity='euclidean', linkage='ward')

cluster.fit_predict(X)

Hier geben wir die Cluster an, was kein Hyperparameter ist. Wir übergeben es jedoch nur, um die Vorhersageklassen klar zu machen. Wir würden die Funktion fit_predict verwenden, um die Klassen über X zu trainieren und vorherzusagen.

Es ist wichtig zu beachten, dass agglomeratives Clustering häufiger verwendet wird als divisives, da es einfacher auszuführen ist. Die Idee, Cluster basierend auf Näherungsmatrizen zusammenzuführen, scheint einfacher zu sein, als einen Cluster über einen Mechanismus in zwei Teile zu teilen.

Lesen Sie: Scikit-learn in Python: Funktionen, Voraussetzungen, Vor- und Nachteile

Um klar zu verstehen, was oben passiert ist, schauen Sie sich die Schritte des Algorithmus an:

Funktionsweise des Algorithmus

Hier sind die Schritte zum Ausführen des agglomerativen Clusterings:

1. Definieren Sie jeden Datenpunkt als Cluster
2. Berechnen Sie die anfängliche Näherungsmetrik
3. Führen Sie zwei Cluster zusammen, die basierend auf der Metrik am „nächsten“ oder ähnlich sind
4. Überarbeiten Sie die Näherungsmetrik und wiederholen Sie den dritten Schritt, bis ein einzelner Cluster übrig bleibt.

Hier müssen also nur noch die Auswirkungen verschiedener Näherungsmethoden verstanden werden. Wie Sie wissen, gibt es beim hierarchischen Clustering hauptsächlich vier Arten von Proximity-Methoden. Dies wird auch als Inter-Cluster-Ähnlichkeit bezeichnet.

Die Methoden (oder Verknüpfungen, wie im Code definiert) umfassen:

1. MIN oder Einzelgestänge
2. MAX oder vollständige Verknüpfung
3. Durchschnittliche Verknüpfung
4. Schwerpunktverknüpfung
5. Ausschließliche Funktionen objektiver Funktionen

Die Ergebnisse derselben können leicht visualisiert werden, indem die Verknüpfungsoption beim Erstellen der Dendrogramme angewendet wird.

Um die Ausgabe des Modells zu visualisieren, benötigen wir nur ein kleines Code-Snippet wie folgt:

plt.scatter(X[:,0],X[:,1], c=cluster.labels_, cmap='winter')

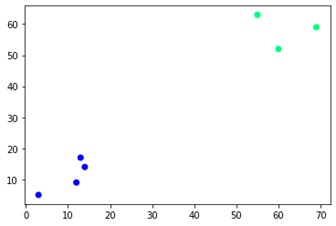
Wie Sie sehen können, befinden sich an den gegenüberliegenden Ecken zwei verschiedene Cluster. Sie können auch mit Clusternummern herumspielen und unterschiedliche Ergebnisse sehen. Das Ganze kann durch Schneiden von Dendrogrammen gesteuert werden. Um das zu verstehen, schreiben wir einen kleinen Ausschnitt für die Visualisierung der Erstellung von Dendrogrammen.

Wir werden Dendrogramm- und Verknüpfungsfunktionen aus dem Modul scipy.cluster.hierarchy verwenden. Hier definieren wir die Verknüpfung, die wir verwenden möchten. Wir müssen dieses Objekt an die Dendrogram-Funktion übergeben, um die Hierarchie zu generieren.

aus scipy.cluster.hierarchy Import Dendrogramm, Verknüpfung

linked = linkage(X, 'complete')

labelList = Bereich (1, 8)

plt.figure(figsize=(10, 7))

Dendrogramm (verknüpft,

Ausrichtung='oben',

Etiketten=Etikettenliste,

distance_sort='absteigend',

show_leaf_counts=Wahr)

plt.show()

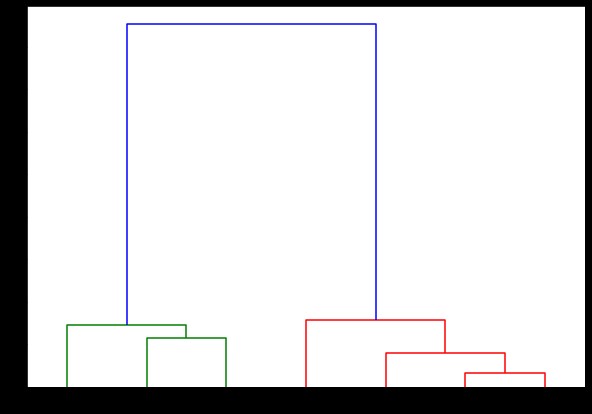
Hier können Sie visualisieren, wie die Cluster bei jeder Iteration gebildet werden. Sie können also das Dendrogramm auf jeder gewünschten Ebene schneiden , und Sie würden am Ende so viele Cluster erhalten. Daher können Sie aufgrund dieser Hierarchiebildung die Anzahl der Cluster nach nur einem Durchlauf durch den Algorithmus und die Daten variieren. Dies gibt dem hierarchischen Clustering einen Vorteil gegenüber anderen Algorithmen wie K-means.

Sehen wir uns nun an, wie hierarchisches Clustering in Python für einen häufig verwendeten Datensatz verwendet wird: IRIS . Wir würden den Datensatz aus einer lokalen CSV-Datei lesen. und werfen Sie einen Blick darauf, wie der Datensatz aussieht und was wir klassifizieren müssen.

importiere numpy als np

pandas als pd importieren

importiere matplotlib.pyplot als plt

%matplotlib inline

data = pd.read_csv('iris.csv')

data.head()

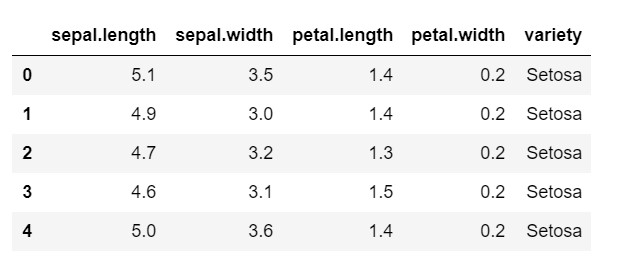
Wie Sie sehen können, ist die Zielvariable die Klasse „Sorte“. Dies ist ein Zeichenfolgenformat, das in Zahlen umgewandelt werden muss, da das Modell codierte Beschriftungen erfordert. Dazu würden wir den Label-Encoder aus der Vorverarbeitungsbibliothek von sklearn verwenden. Eine einfache Anpassung und Transformation, um sie in Zahlen umzuwandeln.

aus der sklearn-Importvorverarbeitung

le = Vorverarbeitung.LabelEncoder()

le.fit(data['variety'])

data['variety'] = le.transform(data['variety'])

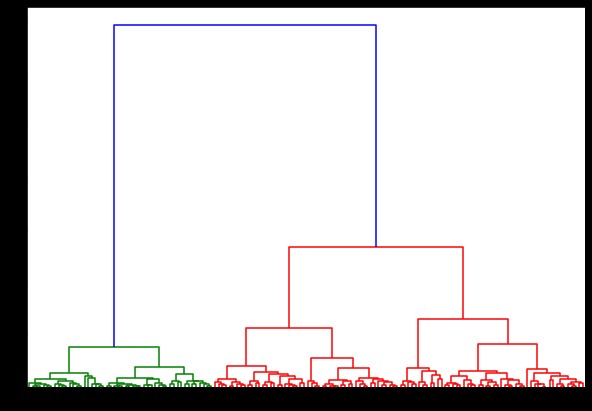
Wenn wir nun darauf ein Dendrogramm erstellen, finden wir verschiedene Iterationen und Abbildungen. So sieht es mit einer einzigen Verknüpfung aus. Wenn wir denselben Code verwenden und ihn mit vollständiger oder Schwerpunktverknüpfung ausführen, würden sich die Dendrogramme etwas unterscheiden. Die Logik bleibt dieselbe, aber unterschiedliche Verknüpfungen würden definitiv die Reihenfolge der Fusion von Clustern beeinflussen.

aus scipy.cluster.hierarchy Import Dendrogramm, Verknüpfung

linked = linkage(data, 'ward')

plt.figure(figsize=(10, 7))

Dendrogramm (verlinkt)

plt.show()

Wenn wir jetzt Clustering auf den Datensatz anwenden, würden wir zwei verschiedene Verknüpfungen verwenden, und Sie würden deutlich sehen, welchen Unterschied es wirklich hat, wenn Sie die Cluster definieren. Wie wir bereits am Label-Encoder gesehen haben, haben wir 3 verschiedene Klassen, also können wir zunächst 3 Cluster anwenden.

aus sklearn.cluster import AgglomerativeClustering

cluster = AgglomerativeClustering(n_clusters=3, affinity='euclidean', linkage='complete')

cluster.fit_predict(Daten)

plt.figure(figsize=(10, 7))

plt.scatter(data['sepal.length'], data['petal.length'], c=cluster.labels_)

Wie Sie der obigen Abbildung entnehmen können, zeigen die Verknüpfungen in der 3-Cluster-Klassifizierung sichtbare Änderungen in der Vorhersage. Schauen Sie sich zuerst die Stationsverknüpfung an. Die Bezeichnungen werden korrekt vorhergesagt, indem der obige Cluster definiert bleibt, obwohl es eine kleine Verwechslung der Werte in den beiden Clustern gibt. Wenn wir jedoch die vollständige Verknüpfung sehen, wird der Cluster aufgeschlüsselt und einige der Werte falsch klassifiziert.

Wie wir bei den Proximity-Methoden wissen, neigt die vollständige Verknüpfung dazu, die größeren Cluster zu brechen, wie wir oben sehen können. Die Stationsmethode oder die Single-Linkage-Methode ist für diese Probleme weniger anfällig. Dies war für die einfachen Datensätze. Lassen Sie uns sehen, wie der Algorithmus leidet und von einigen verrauschten Datensätzen beeinflusst wird.

Ein solcher Datensatz ist der Pulsar-Vorhersagedatensatz oder HTRU2-Datensatz . Der Datensatz ist größer, da er etwa 18.000 Proben enthält. Aus ML-Perspektive betrachtet, hat der Datensatz eine ziemlich normale Größe oder sogar noch weniger. Aber vergleichsweise schwerer als der IRIS-Datensatz. Die Notwendigkeit der Implementierung auf einem abwechslungsreichen Datensatz besteht darin, die Leistung des hierarchischen Clusterings in Python zu analysieren . Um die Möglichkeiten und Vorteile von Implementierungen klar zu verstehen,

pulsar_data = pd.read_csv('pulsar_stars.csv')

pulsar_data.head()

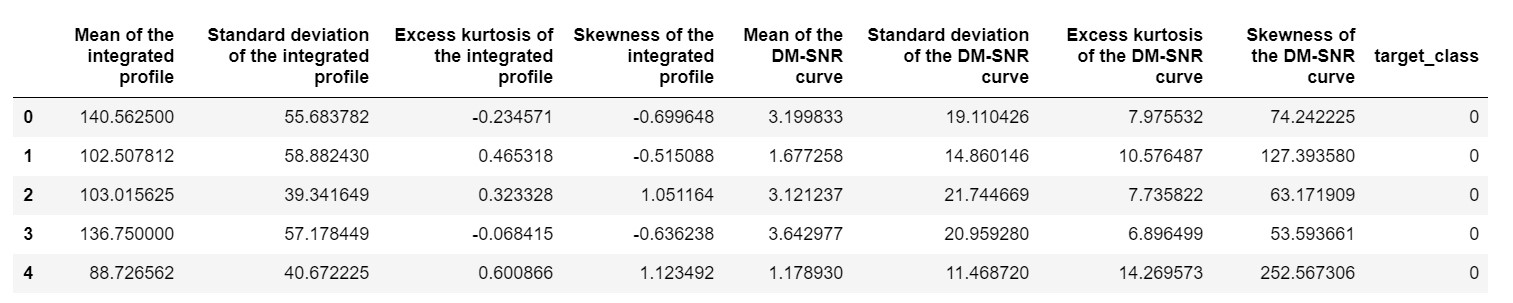
Wir müssten den Datensatz normalisieren, damit er nicht aufgrund von Extremwerten verzerrt wird.

aus sklearn.preprocessing import normalize

pulsar_data = normalisieren (pulsar_data)

Wir würden den Standardcode verwenden, aber dieses Mal messen wir beide Berechnungen.

%%Zeit

aus scipy.cluster.hierarchy Import Dendrogramm, Verknüpfung

linked = linkage(pulsar_data, 'ward')

plt.figure(figsize=(10, 7))

Dendrogramm (verlinkt)

plt.show()

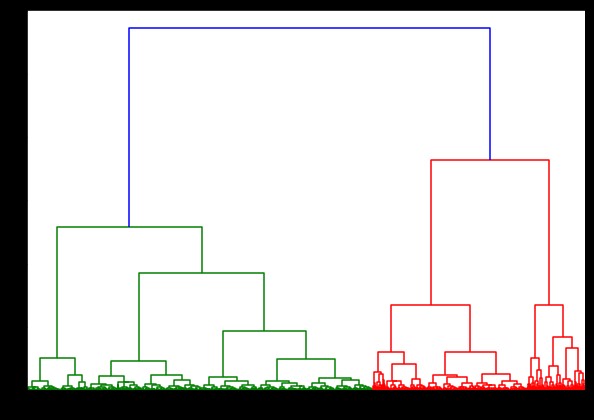
Das Timing zum Generieren eines Dendrogramms auf dem IRIS-Datensatz betrug 6 Sekunden. Das Timing zum Generieren eines Dendrogramms auf dem HTRU2-Datensatz betrug 13 Minuten und 54 Sekunden. Dies ist jedoch nichts im Vergleich zu der Änderung der Vorhersagen aufgrund unterschiedlicher Verknüpfungen, die Sie in dem mit dem HTRU2-Datensatz trainierten Modell beobachten.

Folgen wir dem gleichen Verfahren wie zuvor. Diesmal würden wir Vorhersagen zu jeder Verknüpfung treffen.

Die folgende Abbildung zeigt die Vorhersagen des Clusterings mit jeder Verknüpfung:

cluster = AgglomerativeClustering(n_clusters=2, affinity='euclidean', linkage='average') #sowie complete,ward und single

cluster.fit_predict(pulsar_data)

plt.figure(figsize=(10, 7))

plt.scatter(pulsar_data[:,1], pulsar_data[:,7], c=cluster.labels_)

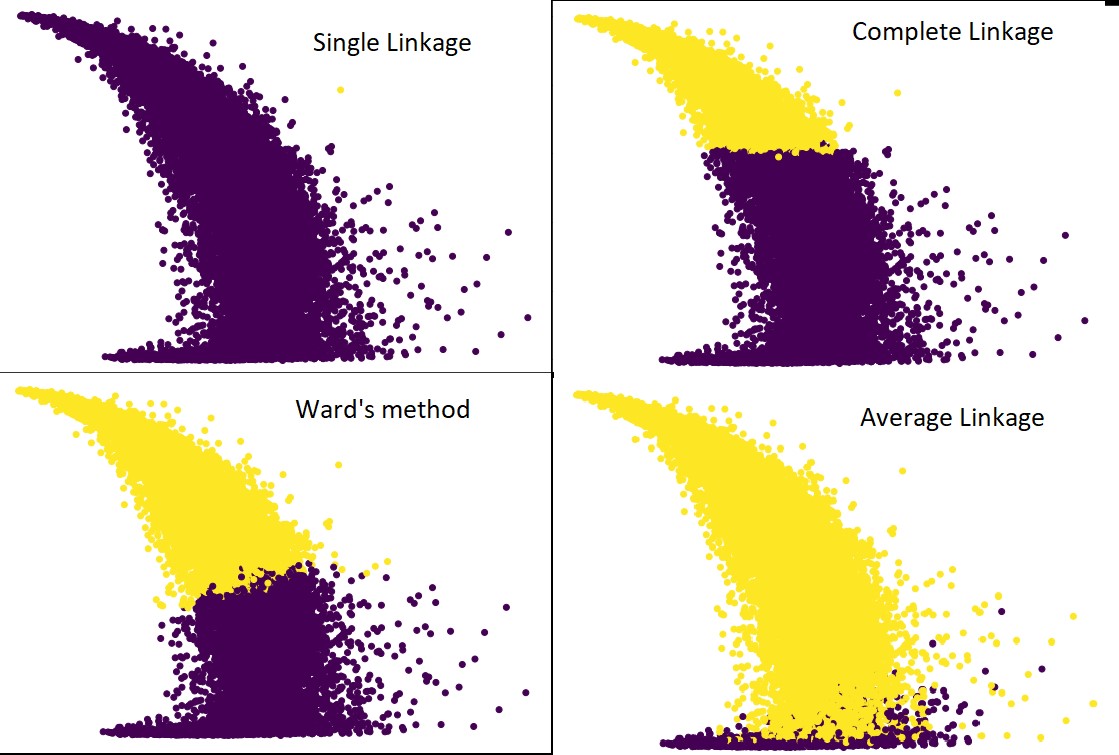
Ja, es ist in der Tat überraschend, wie sehr die Prognosen voneinander abweichen. Dies zeigt die Bedeutung der Nachbarschaftsmatrix beim hierarchischen Clustering.

Wie Sie sehen können, nimmt die einzelne Verknüpfung fast alle Punkte auf, da der Mindestabstand zwischen zwei Clustern die Näherungsmetrik definiert. Dies macht es anfällig für verrauschte Daten. Wenn wir die vollständige Verknüpfung sehen, werden die Daten definitiv in zwei Cluster aufgeteilt, aber möglicherweise hat es den großen Cluster nur aufgrund seiner Nähe gebrochen.

Die durchschnittliche Verknüpfung ist ein Kompromiss zwischen den beiden. Es wird weniger von Rauschen beeinflusst, kann aber immer noch große Cluster aufbrechen, jedoch mit geringerer Wahrscheinlichkeit. Und es handhabt die Klassifizierung besser.

Objektive Funktionen wie die Methode der Station werden manchmal zum Initialisieren anderer Clustering-Methoden wie K-means verwendet. Diese Methode hat genau wie die Average-Linkage einen Kompromiss zwischen der Single- und der Complete-Linkage-Methode. Objektive Funktionen wie die Stationsmethode werden hauptsächlich in kundenspezifischen Lösungen verwendet, um die Wahrscheinlichkeit von Fehlklassifizierungen zu verringern. Und wir sehen, dass es gut funktioniert.

Lernen: Clusteranalyse im Data Mining: Anwendungen, Methoden & Anforderungen

Zeit- und Raumkomplexität

Betrachten Sie zum besseren Verständnis die Art und Weise, wie die Näherungsmetrik definiert und berechnet wird. Die Näherungsmetrik erfordert die Speicherung der Entfernung zwischen jedem Paar von Clustern innerhalb der Datenkarte. Es sorgt für Raumkomplexität: O(n2). Es ist eine große Zahl. Stellen Sie sich zum Vergleich vor, wir hätten 1.000.000 Punkte. Damit steigt der Platzbedarf auf 1012 Punkte. Wenn wir einen groben und schweren Durchschnitt nehmen, indem wir die Größe eines Punktes als Byte annähern, erhalten wir die Datengröße bei 1 TB. Und das muss im RAM gespeichert werden, nicht auf der Festplatte.

Zweitens kommt die zeitliche Komplexität. Für die Notwendigkeit, die Näherungsmatrix bei jeder Iteration zu scannen und zu berücksichtigen, dass wir n Schritte unternehmen, erhalten wir die Komplexität als O(n3). Es ist rechenintensiv, insbesondere bei großen Datensätzen.

Es kann möglich sein, es auf O (n2logn) zu bringen, aber es ist immer noch zu teuer im Vergleich zu anderen Clustering-Algorithmen wie K-means. Wenn Sie mehr über die Analyse der räumlichen und zeitlichen Komplexität von Algorithmen und die Optimierung der Kostenfunktionen erfahren möchten, besuchen Sie die upGrad-Programme in Data Science und Machine Learning.

Einschränkungen

• Die erste Einschränkung haben wir bereits besprochen: Raum- und Zeitkomplexität. Es ist offensichtlich, dass hierarchisches Clustering bei großen Datensätzen nicht günstig ist. Auch wenn die Zeitkomplexität mit schnelleren Rechenmaschinen bewältigt wird, ist die Raumkomplexität zu hoch. Vor allem, wenn wir es in den RAM laden. Und das Problem der Geschwindigkeit nimmt noch mehr zu, wenn wir das hierarchische Clustering in Python implementieren. Python ist langsam, und wenn es um große Aufgaben geht, wird es definitiv darunter leiden.
• Zweitens gibt es keine optimierte Technik mit Nähe. Wenn wir sehen, dass jeder mehrere Probleme und Einschränkungen hat, macht dies den internen Mechanismus des Algorithmus nicht optimiert.
• Wenn wir uns die Clustering-Entscheidungen ansehen, sind sie nicht rückgängig zu machen. Das heißt, sobald das Clustering für eine bestimmte Iteration angewendet wurde, wird es in weiteren Iterationen bis zur Beendigung nicht geändert. Wenn also der Algorithmus aufgrund struktureller Ungenauigkeiten zu irgendeinem Zeitpunkt falsche Cluster zum Kombinieren oder Teilen auswählt, ist dies unwiderruflich.
• Wenn wir uns den Algorithmus genau ansehen, haben wir keine klare Zielfunktion, die minimiert wird. Bei anderen Algorithmen gibt es eine bestimmte Funktion, die wir zu optimieren versuchen. Zum Beispiel haben wir in K-Means eine klare Kostenfunktion, die wir minimieren, was bei hierarchischer Clusterung nicht der Fall ist.

Schauen Sie sich an: Top 9 Data Science-Algorithmen, die jeder Data Scientist kennen sollte

Fazit

Auch wenn es bei großen Datensätzen gewisse Einschränkungen gibt, ist diese Art von Clustering-Algorithmus für kleine bis mittelgroße Datensätze attraktiv. Der hierarchische Clustering-Algorithmus in Python hat aufgrund seines alarmierenden Bedarfs an Zeit- und Platzkomplexität keine große Entwicklung in Architektur oder Schema erlebt.

Und es ist wahr, dass gerade jetzt die Zeit von Big Data ist. Das bedeutet, dass wir Algorithmen benötigen, die besser skalieren. Aber in Fällen, in denen wir uns über die Anzahl der Cluster nicht sicher sind oder die Analyse effizient verfeinern müssen, kann das hierarchische Clustering in Python eine zufriedenstellende Wahl sein.

Damit wissen Sie jetzt, wie Sie hierarchisches Clustering in Python implementieren.

Um mehr über solche Algorithmen und Anwendungen von Methoden in Machine Learning und Data Science zu erfahren, werfen Sie einen Blick auf das Kursangebot von upGrad. Wir haben kumulative Programme für alle Karrierewege, die Sie einschlagen möchten.

Die Programme werden von hochkarätigen Fachleuten sowie den Professoren des IIIT-B kuratiert. Weitere Informationen finden Sie unter upGrad . Wenn Sie neugierig darauf sind, Data Science zu lernen, um an der Spitze des rasanten technologischen Fortschritts zu stehen, sehen Sie sich das Executive PG Program in Data Science von upGrad & IIIT-B an.