Python中的層次聚類【概念與分析】

隨著原始數據流量的增加和分析需求的增加，無監督學習的概念隨著時間的推移變得流行起來。 它用於從由沒有標記目標值的輸入數據組成的數據集中得出見解。 在我們開始討論Python 中的層次聚類並將算法應用於各種數據集之前，讓我們重溫一下聚類的基本思想。

聚類主要處理原始數據的分類。 它包括將彼此最相似的不同數據點組合在一起。 這些組稱為集群，它們是根據定義的相似性或聚類度量形成的。

介紹

層次聚類以樹或定義明確的層次結構的形式處理數據。 該過程涉及一次處理兩個集群。 該算法依賴於相似度或距離矩陣來進行計算決策。 含義，要合併哪兩個集群或如何將集群分成兩個。 考慮到這兩個選項，我們有兩種類型的層次聚類。 如果您是初學者並且有興趣了解有關數據科學的更多信息，請查看我們來自頂尖大學的數據科學課程。

該算法的關鍵方面之一是相似度矩陣（也稱為鄰近矩陣），因為整個算法都基於它進行。 本文將進一步討論許多鄰近方法。

類型

層次聚類有兩種類型：

1. 凝聚聚類
2. 分裂聚類

這些類型是基於基本功能的：開發層次結構的方式。 Agglomerative 是一個自下而上的層次結構生成器，而 Divisive 是一個自上而下的層次結構生成器。

Agglomerative 將所有點作為單獨的集群，然後在每次迭代中合併它們，一次兩個。 Divisive 首先將整個數據假設為一個集群，然後將其劃分，直到所有點都成為單獨的集群。

結果是一組嵌套集群，可以被視為層次樹。 查看它的最佳方法是將集合結構轉換為樹狀圖以查看層次結構。

下面給出了一個樹狀圖與集群表示的簡單示例：

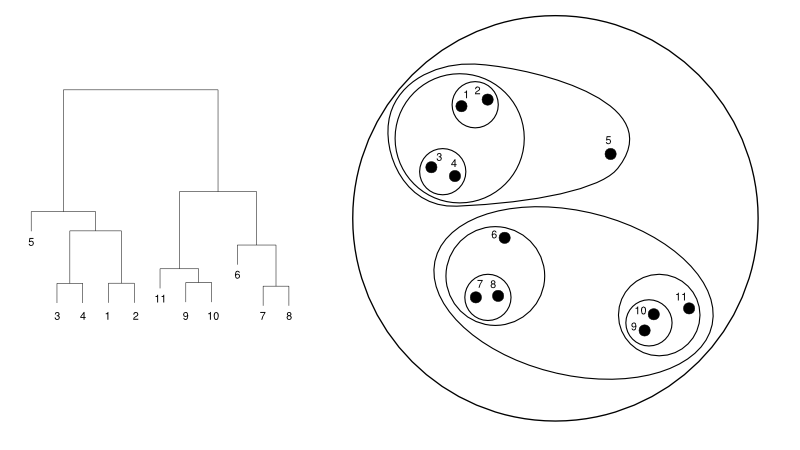
資源

在這裡，聚類可能會以任何一種方式工作，但結果將是一個集群的集合。 數據點 1、2、3、4、5 和 6 一次聚集成兩個。 並且層次結構可以在左圖中看到，它處理相同的樹狀圖。 相同的分析將有助於理解集群的決策。

確定集群的數量

該算法最有用的功能之一是，一旦算法終止，您可以提取任意數量的集群。 它與 K-means 算法完全不同。 在 K-means 中，我們需要傳遞 no-of-clusters 超參數。 這意味著一旦算法完成計算，我們就會擁有那麼多集群。 但是，如果我們以後需要更多的集群，我們就不能輕易地進行調整。 唯一的選擇是更改參數並再次訓練模型。

然而，當涉及到層次聚類時，您可以稍後設置聚類的數量。 最後你可以拿兩個集群。 如果不滿意，您可以採取倒數第二級或更高級別形成的五個集群。 這取決於你。 因此，一旦經過訓練，您無需重新訓練模型即可獲得更多或更少的集群。 它可以通過簡單地將樹狀圖切割到您想要的水平來完成。

了解了概念後，讓我們討論一下Python 中層次聚類的工作原理。

在實驗中，我們將使用 sci-kit learn 庫進行聚類算法。 我們還將使用 SciPy 的 cluster.dendrogram 模塊來可視化和理解限制集群數量的“切割”過程。

將 numpy 導入為 np

X = np.array([[3,5],

[12,9],

[13,17]，

[14,14]，

[60,52],

[55,63],

[69,59],])

在情節上看起來像這樣：

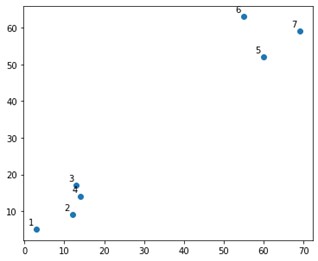
好吧，我們確實看到我們有兩個確定的集群，在頂角和底角。 讓我們看看算法是否可以解決這個問題。

我們將使用 sklearn.clustering 模塊中的 AgglomerativeClustering 函數。

從 sklearn.cluster 導入 AgglomerativeClustering

cluster = AgglomerativeClustering（n_clusters=2，affinity='euclidean'，linkage='ward'）

cluster.fit_predict(X)

在這裡，我們確實指定了集群，這不是超參數。 但是，我們只是傳遞它以使預測類別清晰。 我們將使用 fit_predict 函數來訓練和預測 X 上的類。

需要注意的是，凝聚聚類比分裂聚類更常用，因為它更易於執行。 基於鄰近矩陣合併集群的想法似乎比通過某種機制將集群分成兩個更容易。

閱讀： Python 中的 Scikit-learn：功能、先決條件、優缺點

為了清楚地理解上面發生了什麼，看一下算法中涉及的步驟：

算法的工作

以下是執行凝聚聚類的步驟：

1. 將每個數據點定義為一個集群
2. 計算初始接近度指標
3. 根據指標合併兩個“最接近”或相似的集群
4. 修改鄰近度指標並重複第三步，直到剩下一個集群。

因此，這裡唯一需要了解的是不同鄰近方法的影響。 如您所知，層次聚類中主要有四種鄰近方法。 這也稱為集群間相似性。

方法（或代碼中定義的鏈接）包括：

1. MIN 或單聯動
2. MAX 或完全聯動
3. 平均聯動
4. 質心連桿
5. 目標函數的獨占函數

通過在創建樹狀圖時應用鏈接選項，可以輕鬆地可視化相同的結果。

為了可視化模型的輸出，我們只需要一個小代碼片段，如下所示：

plt.scatter(X[:,0],X[:,1], c=cluster.labels_, cmap='winter')

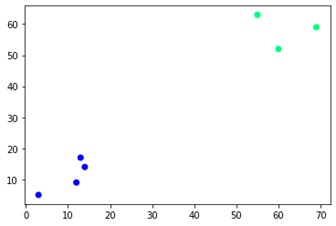
如您所見，對角有兩個不同的集群。 你也可以玩弄簇號並看到不同的結果。 整個事情可以通過切割樹狀圖來驅動。 為了理解這一點，讓我們為樹狀圖創建的可視化編寫一個小片段。

我們將使用 scipy.cluster.hierarchy 模塊中的樹狀圖和鏈接函數。 在這裡，我們定義了我們想要使用的鏈接。 我們需要將該對像傳遞給 dendrogram 函數以生成層次結構。

從 scipy.cluster.hierarchy 導入樹狀圖，鏈接

鏈接=鏈接（X，'完成'）

標籤列表 = 範圍 (1, 8)

plt.figure(figsize=(10, 7))

樹狀圖（鏈接，

方向='頂部'，

標籤=標籤列表，

distance_sort='降序',

show_leaf_counts=真）

plt.show()

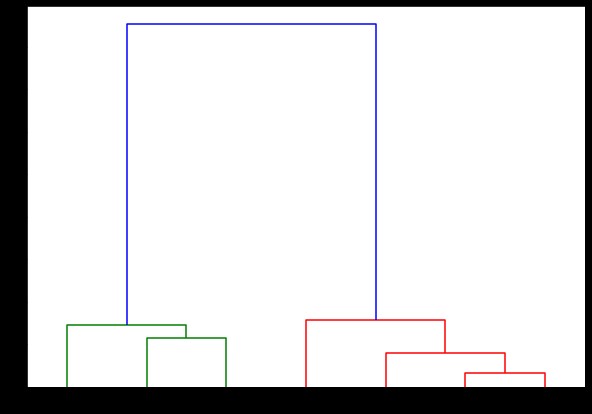
在這裡，您可以可視化每次迭代時集群是如何形成的。 所以，你可以在任何你想要的層次上切割樹狀圖，你最終會得到那麼多簇。 因此，由於這種層次結構的創建，您可能會在僅運行一次算法和數據後改變集群的數量。 它使層次聚類在其他算法（如 K-means）上具有優勢。

現在，讓我們看看如何在 Python中對常用數據集IRIS使用層次聚類。 我們將從本地 csv 讀取數據集。 只需看一下數據集的外觀以及我們需要分類的內容。

將 numpy 導入為 np

將熊貓導入為 pd

將 matplotlib.pyplot 導入為 plt

%matplotlib 內聯

數據 = pd.read_csv('iris.csv')

數據頭（）

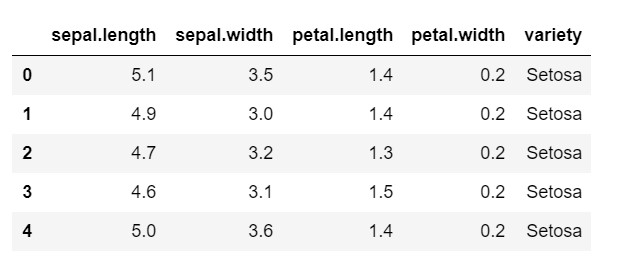
如您所見，目標變量是“品種”類。 這是字符串格式，需要轉換為數字，因為模型需要編碼標籤。 為此，我們將使用 sklearn 預處理庫中的標籤編碼器。 一個簡單的擬合和變換將它們轉換成數字。

從 sklearn 導入預處理

le = preprocessing.LabelEncoder()

le.fit(數據['品種'])

數據['品種'] = le.transform(數據['品種'])

現在，如果我們在此基礎上創建一個樹狀圖，我們會發現各種迭代和映射。 這是使用單個鏈接的外觀。 如果我們使用相同的代碼並使用完整或質心鏈接運行它，則樹狀圖會有所不同。 邏輯是一樣的，但不同的聯繫肯定會影響集群合併的順序。

從 scipy.cluster.hierarchy 導入樹狀圖，鏈接

鏈接=鏈接（數據，“病房”）

plt.figure(figsize=(10, 7))

樹狀圖（鏈接）

plt.show()

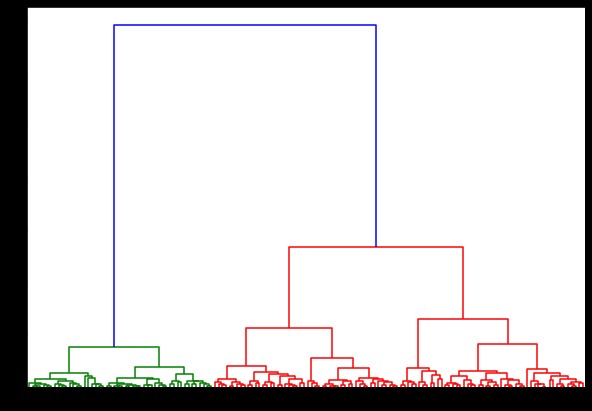
現在，在數據集上應用聚類，我們將使用兩個不同的鏈接，您會清楚地看到它在定義聚類時真正有什麼不同。 正如我們已經從標籤編碼器中看到的那樣，我們有 3 個不同的類，所以我們可能首先應用 3 個集群。

從 sklearn.cluster 導入 AgglomerativeClustering

cluster = AgglomerativeClustering（n_clusters=3，affinity='euclidean'，linkage='complete'）

cluster.fit_predict（數據）

plt.figure(figsize=(10, 7))

plt.scatter(data['sepal.length'], data['petal.length'], c=cluster.labels_)

從上圖中可以看出，在 3-cluster 分類中，鏈接顯示預測的可見變化。 先看病房聯動。 它通過保持上述集群的定義來正確預測標籤，即使兩個集群中的值有少量混合。 但是，當我們看到完整的鏈接時，它會破壞集群並錯誤分類一些值。

正如我們在鄰近方法中所知道的，完整的鏈接確實傾向於破壞較大的集群，正如我們在上面看到的。 病房法或單一聯動法不易受這些問題的影響。 這是針對簡單數據集的。 讓我們看看算法如何受到一些嘈雜數據集的影響和影響。

一個這樣的數據集是 Pulsar 預測數據集或HTRU2 數據集。 數據集更大，因為它包含大約 18,000 個樣本。 如果從 ML 的角度來看，數據集的大小相當規則，甚至更小。 但是，相對而言，它比 IRIS 數據集更重。 在不同數據集上實現的需要是分析Python 中層次聚類的性能。 為了清楚地了解實施的方式和好處，

pulsar_data = pd.read_csv('pulsar_stars.csv')

pulsar_data.head()

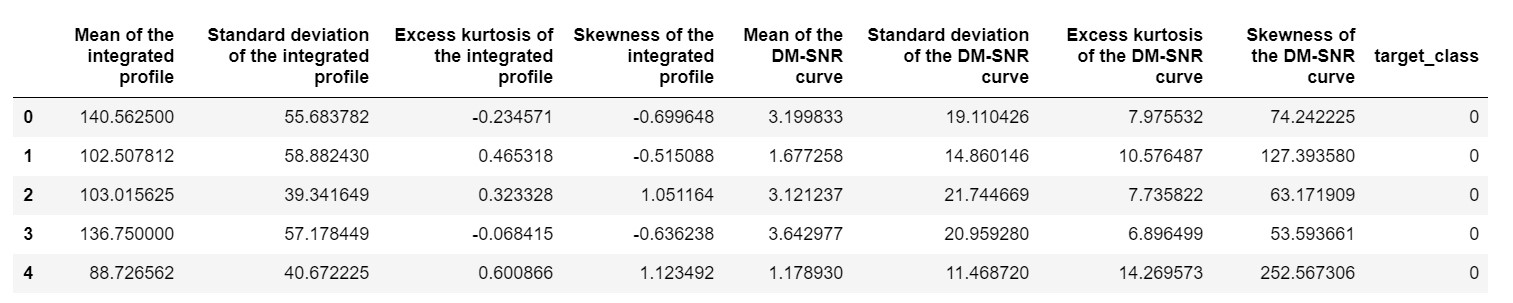
我們需要對數據集進行標準化，使其不會因極端值而出現偏差。

從 sklearn.preprocessing 導入規範化

pulsar_data = 標準化（pulsar_data）

我們將使用標準代碼，但這一次，我們對兩個計算進行計時。

％％時間

從 scipy.cluster.hierarchy 導入樹狀圖，鏈接

鏈接=鏈接（pulsar_data，“病房”）

plt.figure(figsize=(10, 7))

樹狀圖（鏈接）

plt.show()

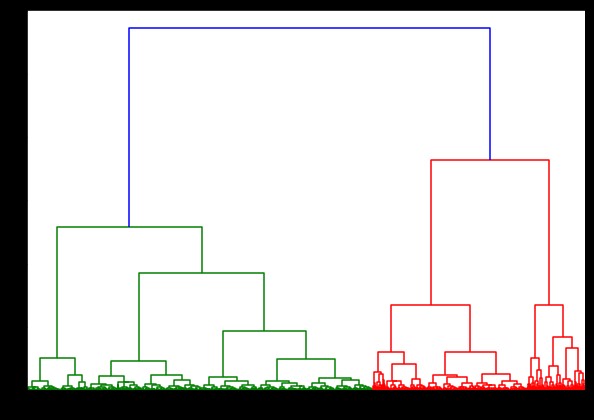
在 IRIS 數據集上生成樹狀圖的時間為 6 秒。 在 HTRU2 數據集上生成樹狀圖的時間為 13 分 54 秒。 但是，與您在使用 HTRU2 數據集訓練的模型中觀察到的不同鏈接導致的預測變化相比，這算不了什麼。

讓我們遵循與之前相同的程序。 這一次，我們將對每一個聯繫做出預測。

下圖顯示了每個鏈接的聚類預測：

cluster = AgglomerativeClustering(n_clusters=2, affinity='euclidean', links='average') #as well as complete,ward and single

cluster.fit_predict(pulsar_data)

plt.figure(figsize=(10, 7))

plt.scatter(pulsar_data[:,1], pulsar_data[:,7], c=cluster.labels_)

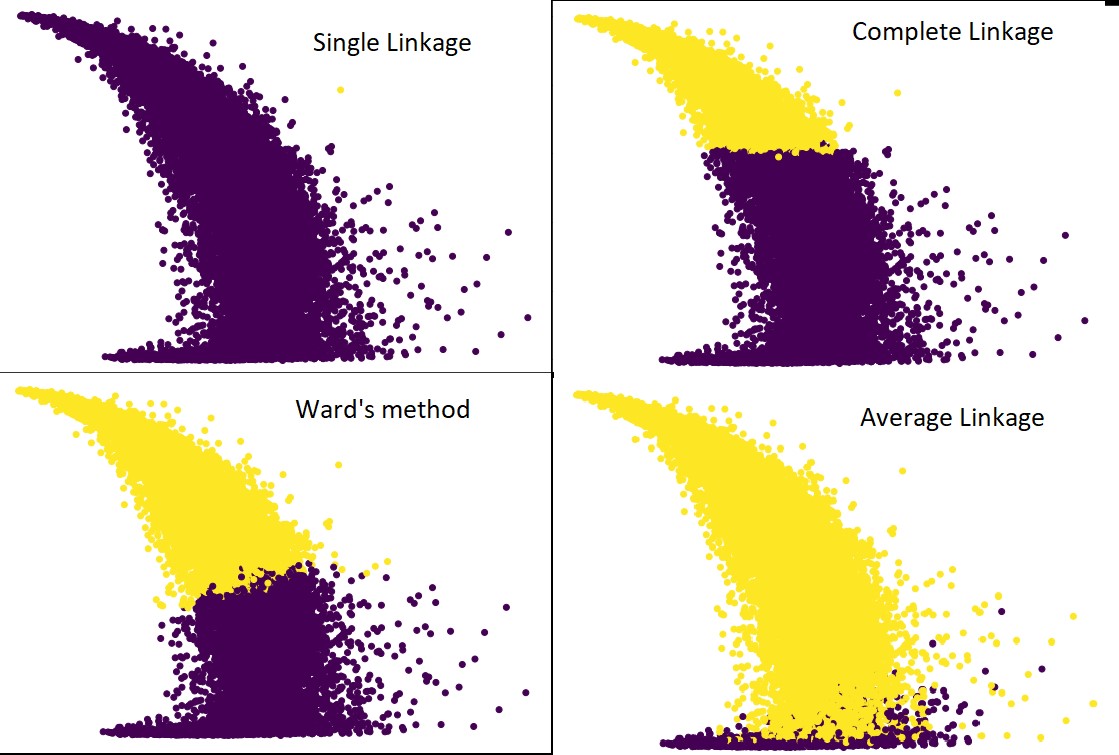
是的，這些預測之間的差異確實令人驚訝。 這表明了鄰近矩陣在層次聚類中的重要性。

如您所見，單個鏈接幾乎包含所有點，因為兩個集群之間的最小距離定義了鄰近度度量。 這使得它容易受到嘈雜數據的影響。 如果我們看到完整的鏈接，它肯定會將數據分成兩個集群，但它可能僅僅因為它的接近而破壞了大集群。

平均聯繫是兩者之間的權衡。 它受噪聲影響較小，但仍可能破壞大型集群，但概率較小。 而且，它確實可以更好地處理分類。

像沃德方法這樣的目標函數有時用於初始化其他聚類方法，如 K-means。 這種方法，就像平均聯動一樣，在單一和完全聯動方法之間進行權衡。 像ward's method這樣的目標函數主要用於定制解決方案，以減少錯誤分類的可能性。 而且，我們確實看到它表現良好。

學習：數據挖掘中的聚類分析：應用、方法和要求

時間和空間複雜度

為了便於理解，請考慮定義和計算鄰近度指標的方式。 鄰近度度量需要存儲數據圖中每對集群之間的距離。 它使空間複雜度：O(n2)。 這是一個很大的數字。 換個角度來看，假設我們有 1,000,000 個點。 這將使空間要求達到 1012 點。 通過將一個點的大小近似為一個字節來粗略地取平均值，我們得到的數據大小為 1TB。 這需要存儲在 RAM 中，而不是硬盤上。

其次，時間複雜度。 由於需要在每次迭代時掃描鄰近矩陣，並且考慮到我們採取 n 步，我們得到的複雜度為 O(n3)。 它的計算成本很高，尤其是在大數據集上。

有可能將其降低到 O(n2logn)，但是與其他聚類算法（如 K-means）相比，它仍然過於昂貴。 如果您想了解更多關於分析算法的空間和時間複雜度以及優化成本函數的信息，您可以前往 upGrad 的數據科學和機器學習課程。

限制

• 我們已經討論了第一個限制：空間和時間複雜度。 很明顯，層次聚類在大數據集的情況下是不利的。 即使用更快的計算機管理時間複雜度，空間複雜度也太高了。 尤其是當我們將它加載到 RAM 中時。 而且，當我們在Python中實現層次聚類時，速度問題會更加嚴重。 Python 很慢，如果涉及到大任務，它肯定會吃虧。
• 其次，沒有優化的接近技術。 如果我們看到每個都有多個問題和限制，這會使算法的內部機制未優化。
• 當我們查看聚類決策時，它們是不可伸縮的。 含義-一旦將聚類應用於確定的迭代，它將不會在進一步的迭代中改變，直到終止。 因此，如果由於結構上的不准確，算法在任何時候選擇了錯誤的集群來合併或拆分，它是不可撤銷的。
• 如果我們仔細觀察算法，我們沒有明確的目標函數被最小化。 在其他算法中，我們嘗試優化一個明確的函數。 例如，在 K-means 中，我們有一個明確的成本函數，我們將其最小化，而層次聚類不是這種情況。

查看：每個數據科學家都應該知道的 9 大數據科學算法

結論

儘管在處理大型數據集時存在一定的局限性，但這種類型的聚類算法在處理中小型數據集時很有吸引力。 由於對時間和空間複雜度的驚人需求， Python 中的層次聚類算法在架構或模式方面沒有太多發展。

而且，現在確實是大數據的時代。 這意味著我們確實需要可擴展性更好的算法。 但是，如果我們不確定集群的數量，或者我們需要有效地改進分析， Python 中的層次聚類可能是一個令人滿意的選擇。

有了這個，您現在知道如何在 Python 中實現層次聚類。

要了解更多此類算法和方法在機器學習和數據科學中的應用，請查看 upGrad 提供的課程。 我們為您想要遵循的任何職業道路提供累積計劃。

這些課程由頂級專業人士以及 IIIT-B 的教授策劃。 有關更多信息，請前往upGrad 。 如果您對學習數據科學以走在快節奏的技術進步的前沿感到好奇，請查看 upGrad 和 IIIT-B 的數據科學執行 PG 計劃。