المجموعات الهرمية في بايثون [المفاهيم والتحليل]

مع زيادة تدفق البيانات الأولية والحاجة إلى التحليل ، أصبح مفهوم التعلم غير الخاضع للإشراف شائعًا بمرور الوقت. يتم استخدامه لرسم رؤى من مجموعات البيانات التي تتكون من بيانات الإدخال دون القيم المستهدفة المعنونة. قبل أن نبدأ في مناقشة التجميع الهرمي في Python وتطبيق الخوارزمية على مجموعات البيانات المختلفة ، دعونا نعيد النظر في الفكرة الأساسية للتجميع.

التجميع يتعامل بشكل أساسي مع تصنيف البيانات الخام. وهو يتألف من تجميع نقاط البيانات المختلفة معًا ، والتي تكون أكثر تشابهًا مع بعضها البعض. تسمى هذه المجموعات المجموعات ، والتي يتم تشكيلها بناءً على التشابه أو مقياس التجميع المحدد.

مقدمة

يتعامل التجميع الهرمي مع البيانات في شكل شجرة أو تسلسل هرمي محدد جيدًا. تتضمن العملية التعامل مع مجموعتين في وقت واحد. تعتمد الخوارزمية على التشابه أو مصفوفة المسافة لاتخاذ القرارات الحسابية. المعنى ، أي مجموعتين يجب دمجهما أو كيفية تقسيم الكتلة إلى مجموعتين. مع وضع هذين الخيارين في الاعتبار ، لدينا نوعان من المجموعات الهرمية . إذا كنت مبتدئًا ومهتمًا بمعرفة المزيد عن علم البيانات ، فراجع دورات علوم البيانات لدينا من أفضل الجامعات.

أحد الجوانب الحرجة للخوارزمية هو مصفوفة التشابه (المعروفة أيضًا باسم مصفوفة القرب) ، حيث تستمر الخوارزمية بأكملها بناءً عليها. هناك العديد من طرق القرب التي تمت مناقشتها بالتفصيل في المقالة.

أنواع

المجموعات الهرمية لها نوعان:

1. التكتل العنقودي
2. المجموعات الانقسامية

الأنواع حسب الوظيفة الأساسية: طريقة تطوير التسلسل الهرمي. التكتل هو منشئ التسلسل الهرمي من أسفل إلى أعلى ، في حين أن الانقسام هو منشئ التسلسل الهرمي من أعلى إلى أسفل.

تأخذ Agglomerative جميع النقاط كمجموعات فردية ثم تدمجها في كل تكرار ، اثنتان في كل مرة. يبدأ الانقسام بافتراض البيانات بأكملها كمجموعة واحدة وتقسيمها حتى تصبح جميع النقاط مجموعات فردية.

والنتيجة هي مجموعة من الكتل المتداخلة التي يمكن اعتبارها شجرة هرمية. أفضل طريقة لعرضها هي تحويل بنية المجموعة إلى مخطط شجيرة لعرض التسلسل الهرمي.

فيما يلي مثال بسيط على مخطط شجر الأسنان مقابل تمثيل الكتلة:

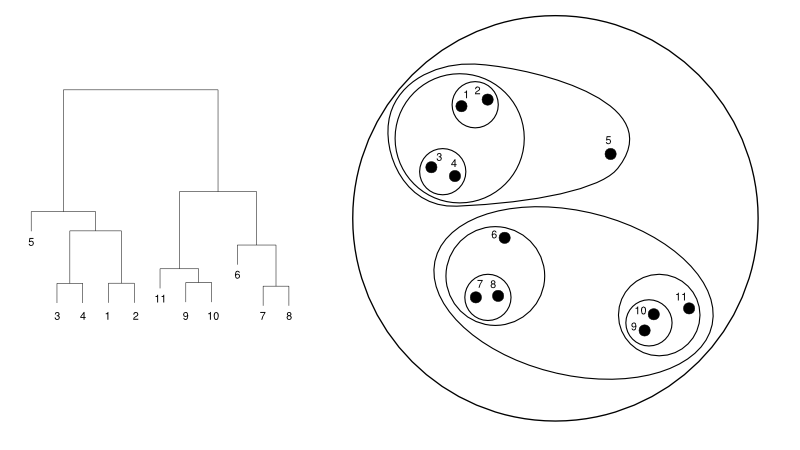
مصدر

هنا ، قد يعمل التجميع في كلتا الحالتين ، لكن النتيجة ستكون مجموعة من الكتل. يتم تجميع نقاط البيانات 1 و 2 و 3 و 4 و 5 و 6 في مجموعتين في وقت واحد. ويمكن رؤية تشكيل التسلسل الهرمي في الشكل الأيسر ، والذي يتعامل مع مخطط الأسنان. سيساعد التحليل نفسه في فهم قرار المجموعات.

تحديد عدد العناقيد

تتمثل إحدى الميزات الأكثر فائدة لهذه الخوارزمية في أنه يمكنك استخراج العديد من المجموعات كما تريد بمجرد إنهاء الخوارزمية. إنها مختلفة تمامًا عن خوارزمية K-mean. في K-mean ، نحتاج إلى اجتياز المعلمة الفوقية no-clusters. هذا يعني أنه بمجرد أن تكمل الخوارزمية الحساب ، سيكون لدينا العديد من المجموعات. ولكن ، إذا احتجنا إلى المزيد من المجموعات لاحقًا ، فلا يمكننا ضبط ذلك بسهولة. سيكون الخيار الوحيد هو تغيير المعلمة وتدريب النموذج مرة أخرى.

حيث أنه عندما يتعلق الأمر بالتجميع الهرمي ، يمكنك تعيين عدد المجموعات لاحقًا. يمكنك أن تأخذ مجموعتين في النهاية. إذا لم تكن راضيًا ، يمكنك أن تأخذ المجموعات الخمس التي تشكلت في الخطوة قبل الأخيرة أو الخطوة ذات المستوى الأعلى. انه يعتمد عليك. ومن ثم ، بمجرد التدريب ، لا تحتاج إلى إعادة تدريب النموذج للحصول على مجموعات أكثر أو أقل. يمكن تحقيق ذلك ببساطة عن طريق قطع مخطط الأسنان على المستوى الذي تريده.

نظرًا لتوضيح المفاهيم ، دعنا نناقش عمل المجموعات الهرمية في Python .

بالنسبة للتجربة ، سنستخدم مكتبة sci-kit Learn لخوارزميات التجميع. سنستخدم أيضًا الوحدة العنقودية dendrogram من SciPy لتصور وفهم عملية "القطع" للحد من عدد المجموعات.

استيراد numpy كـ np

X = np.array ([[3،5]،

[12،9] ،

[13،17] ،

[14 ، 14] ،

[60،52] ،

[55،63] ،

[69،59] ،])

سيبدو مثل هذا في قطعة أرض:

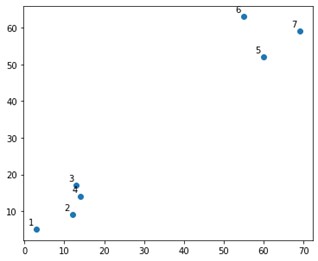
حسنًا ، نرى أن لدينا مجموعتين محددتين ، في الركنين العلوي والسفلي. دعونا نرى ما إذا كانت الخوارزمية يمكنها اكتشاف ذلك أم لا.

سنستخدم وظيفة AgglomerativeClustering من الوحدة النمطية sklearn.clustering.

من sklearn.cluster استيراد AgglomerativeClustering

الكتلة = AgglomerativeClustering (n_clusters = 2 ، التقارب = 'الإقليدية' ، الارتباط = 'Ward')

الكتلة.

هنا ، نحدد المجموعات ، وهي ليست معلمة مفرطة. ومع ذلك ، فإننا نجتازه فقط لتوضيح فصول التنبؤ. سنستخدم الدالة fit_predict للتدريب وكذلك التنبؤ بالفئات التي تزيد عن X.

من المهم أن نلاحظ أن المجموعات التراكمية تستخدم أكثر من الانقسام لأنها أسهل في التنفيذ. تبدو فكرة دمج المجموعات بناءً على مصفوفات التقارب أسهل من تقسيم مجموعة إلى مجموعتين عبر آلية ما.

قراءة: Scikit-Learn in Python: الميزات والمتطلبات المسبقة والإيجابيات والسلبيات

لفهم ما حدث أعلاه بوضوح ، انظر إلى الخطوات المتضمنة في الخوارزمية:

عمل الخوارزمية

فيما يلي خطوات تنفيذ التجميع التراكمي:

1. حدد كل نقطة بيانات كمجموعة
2. احسب مقياس القرب المبدئي
3. ادمج مجموعتين من المجموعات "الأقرب" أو المتشابهة بناءً على المقياس
4. قم بمراجعة مقياس القرب وكرر الخطوة الثالثة حتى تبقى مجموعة واحدة.

لذا ، فإن الشيء الوحيد المتبقي هنا هو تأثير طرق التقارب المختلفة. كما تعلم ، هناك أربعة أنواع من طرق التقارب في المجموعات الهرمية. يُعرف هذا أيضًا باسم التشابه بين المجموعات.

تتضمن الطرق (أو الربط ، كما هو محدد في الكود) ما يلي:

1. MIN أو ربط واحد
2. MAX أو ربط كامل
3. متوسط ​​الارتباط
4. الربط المركزي
5. وظائف حصرية للوظائف الموضوعية

يمكن تصور نتائج ذلك بسهولة من خلال تطبيق خيار الربط أثناء إنشاء مخططات الأسنان.

لتصور ناتج النموذج ، نحتاج فقط إلى مقتطف رمز صغير على النحو التالي:

تبعثر plt. (X [:، 0]، X [:، 1]، c = cluster.labels_، cmap = 'فصل الشتاء')

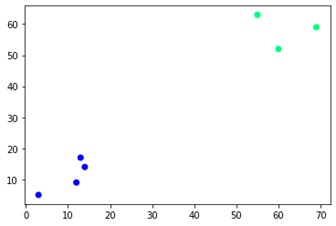
كما ترى ، هناك مجموعتان مختلفتان في الزوايا المقابلة. يمكنك أيضًا اللعب بأرقام المجموعة ورؤية نتائج مختلفة. كل شيء يمكن أن يكون مدفوعا بقطع dendrograms. لفهم ذلك ، دعنا نكتب مقتطفًا صغيرًا لتخيل إنشاء dendrograms.

سنستخدم وظائف dendrogram والربط من الوحدة النمطية scipy.cluster.hierarchy. هنا ، نحدد الارتباط الذي نريد استخدامه. نحتاج إلى تمرير هذا الكائن إلى وظيفة مخطط الأسنان لتوليد التسلسل الهرمي.

من scipy.cluster.hierarchy import dendrogram، linkage

مرتبط = ربط (X، "مكتمل")

LabelList = النطاق (1 ، 8)

شكل plt (حجم التين = (10 ، 7))

dendrogram (مرتبط ،

الاتجاه = 'أعلى' ،

تسميات = LabelsList ،

space_sort = "تنازلي" ،

show_leaf_counts = صحيح)

plt.show ()

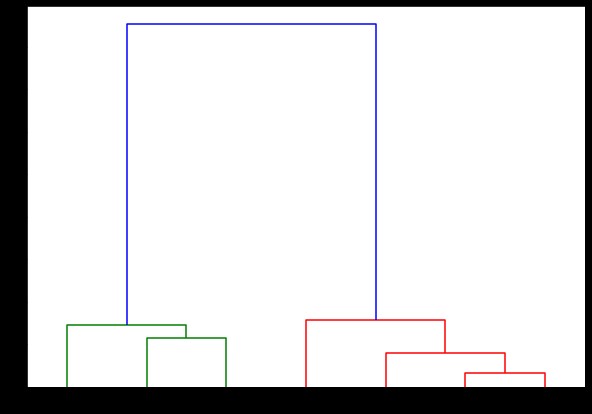
هنا ، يمكنك تصور كيفية تكوين المجموعات في كل تكرار. لذلك ، يمكنك قص مخطط الأسنان على أي مستوى تريده ، وستنتهي بالعديد من المجموعات. ومن ثم ، بسبب إنشاء هذا التسلسل الهرمي ، يمكنك تغيير عدد المجموعات بعد تشغيل واحد فقط من خلال الخوارزمية والبيانات. إنه ما يعطي التجميع الهرمي ميزة على الخوارزميات الأخرى مثل K.

الآن ، دعونا نلقي نظرة على كيفية استخدام المجموعات الهرمية في Python على مجموعة بيانات شائعة الاستخدام: IRIS . سنقرأ مجموعة البيانات من ملف CSV محلي. وإلقاء نظرة على شكل مجموعة البيانات وما نحتاج إلى تصنيفها.

استيراد numpy كـ np

استيراد الباندا كما pd

استيراد matplotlib.pyplot كـ PLT

٪ matplotlib مضمنة

data = pd.read_csv ('iris.csv')

data.head ()

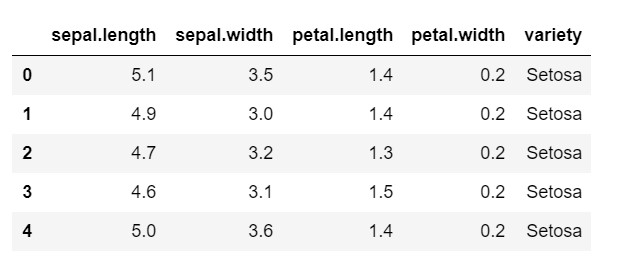
كما ترى ، المتغير الهدف هو فئة "التنوع". هذا بتنسيق سلسلة يجب تحويله إلى أرقام ، حيث يتطلب النموذج تسميات مشفرة. للقيام بذلك ، سنستخدم أداة تشفير التسمية من مكتبة المعالجة المسبقة في sklearn. تناسب بسيط وتحويلها لتحويلها إلى أرقام.

من sklearn استيراد التجهيز المسبق

le = المعالجة المسبقة.

le.fit (بيانات ["تنوع"])

البيانات ['Variety'] = le.transform (البيانات ["متنوعة"])

الآن ، إذا أنشأنا مخطط شجيرة على هذا ، فسنجد تكرارات وخرائط مختلفة. هذه هي الطريقة التي تبدو بها مع ارتباط واحد. إذا استخدمنا نفس الكود وقمنا بتشغيله مع ارتباط كامل أو سنترويد ، فإن مخططات التشعب سوف تختلف قليلاً. يبقى المنطق كما هو ، لكن الروابط المختلفة ستؤثر بالتأكيد على ترتيب اندماج المجموعات.

من scipy.cluster.hierarchy import dendrogram، linkage

مرتبط = ربط (بيانات ، "جناح")

شكل plt (حجم التين = (10 ، 7))

dendrogram (مرتبط)

plt.show ()

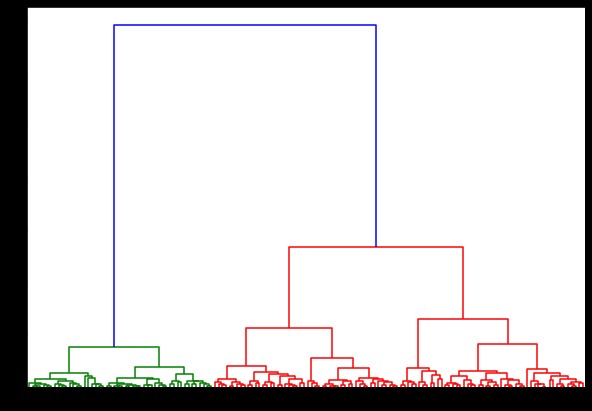
الآن ، بتطبيق التجميع على مجموعة البيانات ، سنستخدم رابطين مختلفين ، وسترى بوضوح الاختلاف الذي يحدثه حقًا أثناء تحديد المجموعات. كما رأينا بالفعل من برنامج تشفير الملصقات ، لدينا 3 فئات مختلفة ، لذلك قد نطبق 3 مجموعات في البداية.

من sklearn.cluster استيراد AgglomerativeClustering

الكتلة = AgglomerativeClustering (n_clusters = 3 ، التقارب = 'الإقليدية' ، الارتباط = 'كامل')

الكتلة.فيت_توقع (البيانات)

شكل plt (حجم التين = (10 ، 7))

plt.scatter (البيانات ['sepal.length'] ، البيانات ['petal.length'] ، c = cluster.labels_)

كما ترى من الشكل أعلاه ، في تصنيف المجموعات الثلاث ، تُظهر الروابط تغييرات واضحة في التنبؤ. انظر إلى رابط الجناح أولاً. يتنبأ بالتسميات بشكل صحيح عن طريق الحفاظ على تحديد المجموعة أعلاه ، على الرغم من وجود مزيج صغير من القيم في المجموعتين. ولكن عندما نرى الارتباط الكامل ، فإنه يكسر الكتلة ويخطئ في تصنيف بعض القيم.

كما نعلم في طرق القرب ، فإن الارتباط الكامل يميل إلى كسر المجموعات الأكبر ، كما نرى أعلاه. طريقة القاصر أو طريقة الربط الفردي أقل عرضة لهذه المشكلات. كان هذا لمجموعات البيانات البسيطة. دعونا نرى كيف تعاني الخوارزمية وتتأثر ببعض مجموعات البيانات الصاخبة.

إحدى مجموعات البيانات هذه هي مجموعة بيانات التنبؤ Pulsar أو مجموعة بيانات HTRU2 . مجموعة البيانات أكبر ، حيث تحتوي على حوالي 18000 عينة. إذا تم رؤيتها من منظور ML ، فإن مجموعة البيانات تكون ذات حجم عادي إلى حد ما ، أو حتى أقل. لكنها ، نسبيًا ، أثقل من مجموعة بيانات IRIS. تتمثل الحاجة إلى التنفيذ على مجموعة بيانات متنوعة في تحليل أداء المجموعات الهرمية في Python . لفهم طرق وامتيازات عمليات التنفيذ بوضوح ،

pulsar_data = pd.read_csv ('pulsar_stars.csv')

pulsar_data.head ()

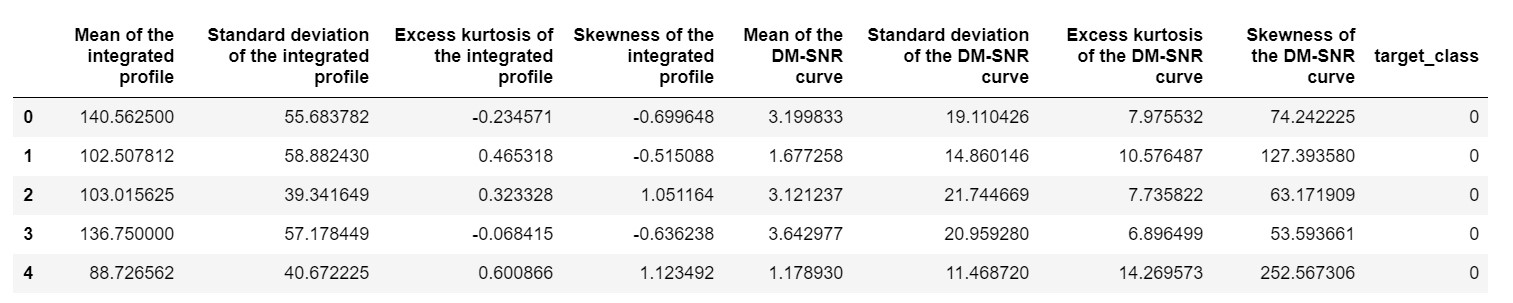
سنحتاج إلى تطبيع مجموعة البيانات بحيث لا يتم تحيزها بسبب القيم المتطرفة.

من sklearn.preprocessing تطبيع الاستيراد

pulsar_data = تطبيع (pulsar_data)

سنستخدم الكود القياسي ، لكن هذه المرة ، سنقوم بتوقيت كلتا العمليتين الحسابيتين.

٪٪زمن

من scipy.cluster.hierarchy import dendrogram، linkage

مرتبط = ارتباط (بيانات بولسار ، "جناح")

شكل plt (حجم التين = (10 ، 7))

dendrogram (مرتبط)

plt.show ()

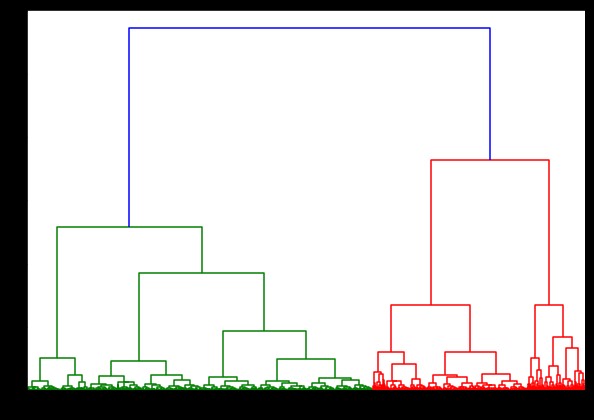
كان توقيت إنشاء dendrogram على مجموعة بيانات IRIS 6 ثوانٍ. كان توقيت إنشاء مخطط شجر على مجموعة بيانات HTRU2 13 دقيقة و 54 ثانية. لكن هذا لا يعد شيئًا مقارنة بالتغيير في التنبؤات بسبب الروابط المختلفة ، والتي لاحظتها في النموذج المُدرَّب باستخدام مجموعة بيانات HTRU2.

دعونا نتبع نفس الإجراء كما فعلنا من قبل. هذه المرة سنقوم بعمل تنبؤات حول كل ارتباط.

يوضح الشكل التالي تنبؤات التجميع مع كل ارتباط:

الكتلة = الكتلة التجميعية (n_clusters = 2 ، التقارب = 'الإقليدية' ، الارتباط = 'المتوسط') # وكذلك كاملة ، وارد وأفراد

الكتلة.

شكل plt (حجم التين = (10 ، 7))

مبعثر plt (pulsar_data [:، 1]، pulsar_data [:، 7]، c = cluster.labels_)

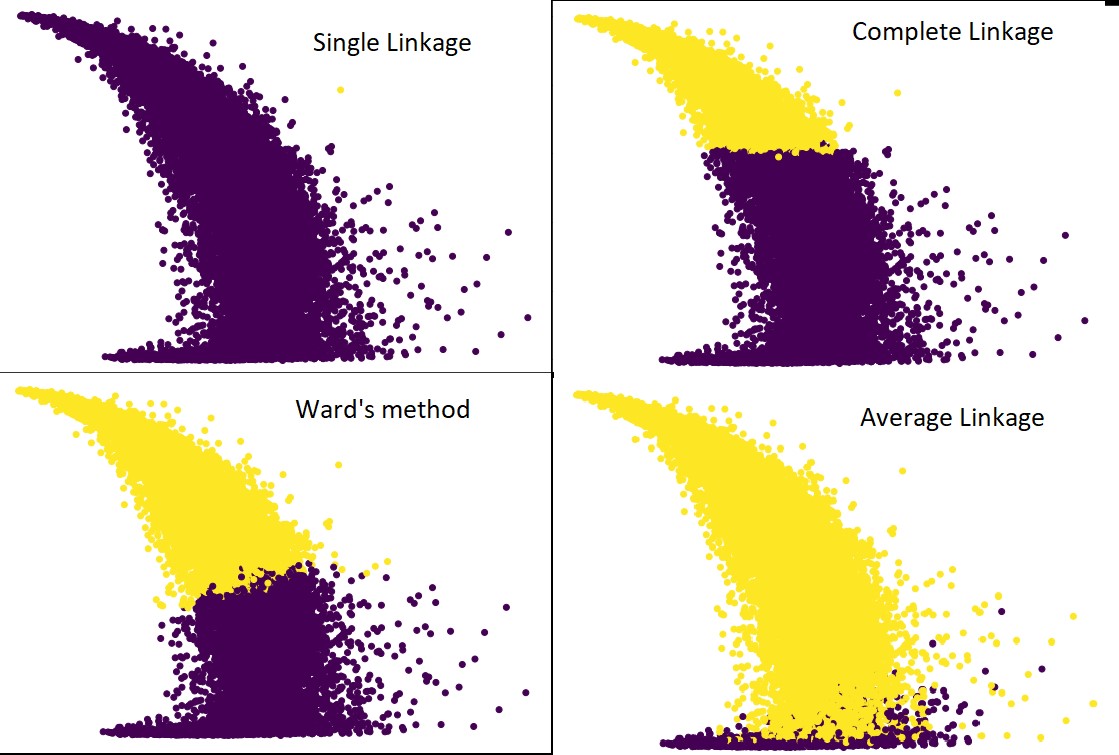
نعم ، من المدهش حقًا مدى اختلاف التوقعات عن بعضها البعض. يوضح هذا أهمية مصفوفة التقارب في التجميع الهرمي.

كما ترى ، يأخذ الارتباط الفردي جميع النقاط تقريبًا حيث أن الحد الأدنى للمسافة بين مجموعتين يحدد مقياس القرب. هذا يجعلها عرضة للبيانات الصاخبة. إذا رأينا الارتباط الكامل ، فمن المؤكد أنه يقسم البيانات إلى مجموعتين ، ولكن ربما يكون قد كسر الكتلة الكبيرة فقط بسبب قربه.

متوسط ​​الارتباط هو مقايضة بين الاثنين. إنه أقل تأثراً بالضوضاء ، لكنه قد يكسر مجموعات كبيرة ، ولكن مع احتمال أقل. وهي تتعامل مع التصنيف بشكل أفضل.

تُستخدم أحيانًا الدوال الموضوعية مثل طريقة القفص لتهيئة طرق التجميع الأخرى مثل K-mean. هذه الطريقة ، مثلها مثل متوسط ​​الارتباط ، لها مفاضلة بين طريقتي الربط الفردي والتام. تُستخدم الوظائف الموضوعية مثل طريقة الجناح بشكل أساسي في الحلول المخصصة لتقليل احتمالية سوء التصنيف. ونرى أنه يعمل بشكل جيد.

تعلم: تحليل الكتلة في استخراج البيانات: التطبيقات والأساليب والمتطلبات

تعقيد الزمان والمكان

فقط لإعطاء فهم ، ضع في اعتبارك الطريقة التي يتم بها تحديد مقياس التقارب وحسابه. يتطلب مقياس القرب تخزين المسافة بين كل زوج من المجموعات داخل خريطة البيانات. يجعل من تعقيد الفضاء: O (n2). إنه عدد كبير. لوضعها في نصابها الصحيح ، تخيل أن لدينا مليون نقطة. سيؤدي ذلك إلى رفع متطلبات المساحة إلى 1012 نقطة. بأخذ متوسط ​​تقريبي وثقيل عن طريق تقريب حجم نقطة واحدة كبايت ، نحصل على حجم البيانات عند 1 تيرابايت. وهذا يحتاج إلى أن يتم تخزينه في ذاكرة الوصول العشوائي ، وليس على القرص الصلب.

ثانيًا ، يأتي التعقيد الزمني. من أجل الحاجة إلى مسح مصفوفة التقارب في كل تكرار مع الأخذ في الاعتبار أننا نتخذ خطوات n ، نحصل على التعقيد كـ O (n3). إنه مكلف حسابيًا ، خاصة في مجموعات البيانات الكبيرة.

قد يكون من الممكن خفضها إلى O (n2logn) ، لكنها لا تزال باهظة الثمن مقارنة بخوارزميات التجميع الأخرى ، مثل K-mean. إذا كنت ترغب في معرفة المزيد حول تحليل تعقيد المكان والزمان للخوارزميات وتحسين وظائف التكلفة ، فيمكنك التوجه إلى upGrad's Programs في علوم البيانات وتعلم الآلة.

محددات

• لقد ناقشنا بالفعل القيد الأول: تعقيد المكان والزمان. من الواضح أن التجميع الهرمي غير مناسب في حالة مجموعات البيانات الكبيرة. حتى إذا تمت إدارة تعقيدات الوقت باستخدام آلات حسابية أسرع ، فإن تعقيد المساحة يكون مرتفعًا للغاية. خاصة عندما نقوم بتحميله في ذاكرة الوصول العشوائي. وتزداد مسألة السرعة بشكل أكبر عندما نطبق التجميع الهرمي في بايثون. بايثون بطيئة ، وإذا كان الأمر يتعلق بالمهام الكبيرة ، فإنها ستعاني بالتأكيد.
• ثانيًا ، لا توجد تقنية مُحسَّنة مع القرب. إذا رأينا أن لكل منها مشاكل وقيود متعددة ، فإن هذا يجعل الآلية الداخلية للخوارزمية غير محسَّنة.
• عندما ننظر إلى قرارات التجميع ، لا يمكن التراجع عنها. المعنى - بمجرد تطبيق التجميع لتكرار محدد ، لن يتم تغييره في المزيد من التكرارات حتى الإنهاء. لذلك ، إذا كانت الخوارزمية ، بسبب عدم الدقة الهيكلية ، تختار ، في أي وقت ، مجموعات خاطئة للجمع أو الانقسام ، فلا رجوع عنها.
• إذا نظرنا عن كثب إلى الخوارزمية ، فليس لدينا وظيفة موضوعية واضحة يتم تصغيرها. في الخوارزميات الأخرى ، هناك وظيفة محددة نحاول تحسينها. على سبيل المثال ، في K يعني أن لدينا وظيفة تكلفة واضحة نقوم بتقليلها ، وهذا ليس هو الحال مع المجموعات الهرمية.

تحقق من: أفضل 9 خوارزميات لعلوم البيانات يجب أن يعرفها كل عالم بيانات

خاتمة

على الرغم من وجود قيود معينة عندما يتعلق الأمر بمجموعات البيانات الكبيرة ، فإن هذا النوع من خوارزمية التجميع جذاب أثناء التعامل مع مجموعات البيانات الصغيرة إلى المتوسطة الحجم. لم تشهد خوارزمية التجميع الهرمي في Python الكثير من التطور في الهندسة المعمارية أو المخطط بسبب حاجتها المزعجة للوقت وتعقيد المكان.

وصحيح أنه في الوقت الحالي ، حان الوقت للبيانات الضخمة. هذا يعني أننا نحتاج إلى خوارزميات تتوسع بشكل أفضل. ولكن ، مع ذلك ، في الحالات التي لا نكون فيها متأكدين من عدد المجموعات ، أو نحتاج إلى تحسين التحليل بكفاءة ، يمكن أن يكون التجميع الهرمي في Python اختيارًا مرضيًا.

بهذا ، تعرف الآن كيفية تنفيذ المجموعات الهرمية في Python.

لفهم المزيد من هذه الخوارزميات وتطبيقات الأساليب في التعلم الآلي وعلوم البيانات ، ألق نظرة على عروض الدورات التي تقدمها upGrad. لدينا برامج تراكمية لأي من المسارات الوظيفية التي تريد اتباعها.

يتم تنسيق البرامج من قبل كبار المتخصصين وكذلك أساتذة في IIIT-B. لمزيد من المعلومات ، توجه إلى upGrad . إذا كنت مهتمًا بتعلم علم البيانات ليكون في مقدمة التطورات التكنولوجية السريعة ، فراجع برنامج upGrad & IIIT-B التنفيذي في علوم البيانات.