Алгоритм опорных векторов в машинном обучении

Все, что вам нужно знать об алгоритмах опорных векторов

Большинство новичков, когда дело доходит до машинного обучения, естественным образом начинают с алгоритмов регрессии и классификации . Эти алгоритмы просты и им легко следовать. Однако важно выйти за рамки этих двух алгоритмов машинного обучения, чтобы лучше понять концепции машинного обучения.

В области машинного обучения можно узнать гораздо больше, что может быть не так просто, как регрессия и классификация, но может помочь нам решить различные сложные проблемы. Позвольте познакомить вас с одним из таких алгоритмов — алгоритмом опорных векторов . Алгоритм машины опорных векторов или алгоритм SVM обычно называют одним из таких алгоритмов машинного обучения, который может обеспечить эффективность и точность как для задач регрессии, так и для задач классификации.

Если вы мечтаете сделать карьеру в области машинного обучения, то машина опорных векторов должна стать частью вашего учебного арсенала. В upGrad мы стремимся вооружить наших студентов лучшими алгоритмами машинного обучения, чтобы они могли начать свою карьеру. Вот что, по нашему мнению, может помочь вам начать работу с алгоритмом SVM в машинном обучении.

Что такое алгоритм опорных векторов?

SVM — это тип алгоритма обучения с учителем, который стал очень популярным в 2020 году и останется таковым в будущем. История SVM восходит к 1990 году; он взят из статистической теории обучения Вапника. SVM можно использовать как для задач регрессии, так и для задач классификации; однако он в основном используется для решения задач классификации.

SVM — это дискриминационный классификатор, который создает гиперплоскости в N-мерном пространстве, где n — количество признаков в наборе данных, помогающих различать будущие входные данные. Звучит запутанно, не волнуйтесь, мы поймем это простым языком.

Как работает алгоритм опорных векторов?

Прежде чем углубляться в работу SVM, давайте разберемся с некоторыми ключевыми терминами.

Гиперплоскость

Гиперплоскости, которые также иногда называют границами решений или плоскостями решений, — это границы, которые помогают классифицировать точки данных. Сторону гиперплоскости, куда попадает новая точка данных, можно выделить или отнести к разным классам. Размер гиперплоскости зависит от количества объектов, которые относятся к набору данных. Если в наборе данных есть 2 объекта, то гиперплоскость может быть простой линией. Когда набор данных имеет 3 объекта, гиперплоскость является двумерной плоскостью.

Векторы поддержки

Опорные векторы — это точки данных, которые находятся ближе всего к гиперплоскости и влияют на ее положение. Поскольку эти векторы влияют на позиционирование гиперплоскости, они называются опорными векторами и, следовательно, называются алгоритмом опорных векторов.

Поле

Проще говоря, запас — это зазор между гиперплоскостью и опорными векторами. SVM всегда выбирает гиперплоскость, которая максимизирует запас. Чем больше маржа, тем выше точность результатов. В алгоритмах SVM используются два типа полей: жесткие и мягкие.

Когда набор обучающих данных является линейно разделимым, SVM может просто выбрать две параллельные линии, которые максимизируют предельное расстояние; это называется жесткая маржа. Когда набор обучающих данных не полностью линейно разделен, SVM допускает некоторое нарушение поля. Это позволяет некоторым точкам данных оставаться на неправильной стороне гиперплоскости или между границей и гиперплоскостью, чтобы не снижалась точность; это называется мягкой маржей.

Для данного набора данных может быть много возможных гиперплоскостей. Цель VSM — выбрать максимальное поле для классификации новых точек данных по разным классам. Когда добавляется новая точка данных, SVM определяет, на какую сторону гиперплоскости падает точка данных. В зависимости от стороны гиперплоскости, на которую попадает новая точка данных, SVM затем классифицирует ее по разным классам.

Читайте: Линейная алгебра для машинного обучения: важные концепции, зачем учиться до машинного обучения

Какие существуют типы машин опорных векторов?

На основе обучающего набора данных алгоритмы SVM могут быть двух типов:

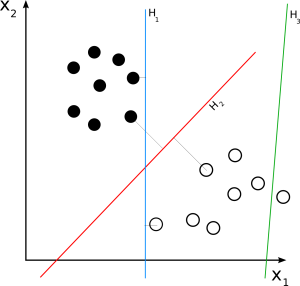
Линейный метод опорных векторов

Источник

Линейный SVM используется для линейно разделимого набора данных. Простой пример из реальной жизни может помочь нам понять работу линейного SVM. Рассмотрим набор данных, который имеет одну характеристику — вес человека. Предполагается, что точки данных можно разделить на два класса: страдающие ожирением и не страдающие ожирением. Чтобы классифицировать точки данных по этим двум классам, SVM может создать гиперплоскость с максимальным запасом с помощью ближайших опорных векторов. Теперь всякий раз, когда добавляется новая точка данных, SVM определяет сторону гиперплоскости, на которую она падает, и классифицирует человека как страдающего ожирением или нет.

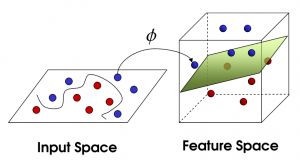
Нелинейный SVM

Источник

По мере увеличения количества признаков линейное разделение набора данных становится сложной задачей. Вот где используется нелинейный SVM. Мы не можем провести прямую линию для разделения точек данных, если набор данных не является линейно разделимым. Поэтому, чтобы разделить эти точки данных, SVM добавляет еще одно измерение. Новое измерение z можно рассчитать как z = x2 + Y2. Этот расчет поможет разделить функции набора данных в линейной форме, а затем SVM может создать гиперплоскость для классификации точек данных.

Когда точка данных преобразуется в пространство высокой размерности путем добавления нового измерения, она становится легко отделимой с помощью гиперплоскости. Это делается с помощью так называемого трюка с ядром. С помощью трюка с ядром алгоритмы SVM могут преобразовывать неразделимые данные в разделяемые.

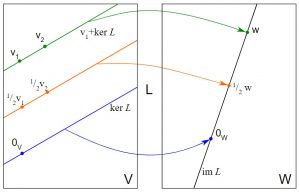
Что такое ядро?

Ядро — это функция, которая принимает входные данные низкой размерности и преобразует их в пространство высокой размерности. Его также называют параметром настройки, который помогает повысить точность выходных данных SVM. Они выполняют некоторые сложные преобразования данных, чтобы преобразовать неразделимый набор данных в разделяемый.

Источник

Какие существуют типы ядер SVM?

Линейное ядро

Как следует из названия, линейное ядро ​​используется для линейно разделимых наборов данных. Он в основном используется для наборов данных с большим количеством функций, например, для классификации текста, где все алфавиты являются новой функцией. Синтаксис линейного ядра:

К (х, у) = сумма (х * у)

x и y в синтаксисе — это два вектора.

Обучение SVM с линейным ядром происходит быстрее, чем с любым другим ядром, поскольку требует оптимизации только параметра регуляризации C, а не параметра гаммы.

Полиномиальное ядро

Полиномиальное ядро ​​— это более обобщенная форма линейного ядра, полезная при преобразовании нелинейного набора данных. Формула ядра полинома выглядит следующим образом:

К(х, у) = (хТ*у + с)d

Здесь x и y — два вектора, c — константа, допускающая компромисс между членами более высокой и более низкой размерности, а d — порядок ядра. Разработчик должен определить порядок ядра вручную в алгоритме.

Ядро радиальной базисной функции

Ядро радиальной базисной функции, также называемое ядром Гаусса, является широко используемым ядром в алгоритмах SVM для решения задач классификации. Он может отображать входные данные в неопределенное многомерное пространство. Ядро радиальной базисной функции может быть математически представлено как:

K(x, y) = exp(-gamma*sum(x – y2))

Здесь x и y — два вектора, а гамма — параметр настройки в диапазоне от 0 до 1. Гамма задается вручную в алгоритме обучения.

Линейные, полиномиальные и радиальные базисные функции отличаются математическим подходом к принятию решений о создании гиперплоскости и точностью. Линейные и полиномиальные ядра требуют меньше времени на обучение, но обеспечивают меньшую точность. С другой стороны, ядро ​​радиальной базисной функции требует больше времени для обучения, но обеспечивает более высокую точность результатов.

Теперь возникает вопрос, как выбрать, какое ядро ​​использовать для вашего набора данных. Ваше решение должно зависеть исключительно от сложности набора данных и точности результатов, которые вы хотите получить. Конечно, всем нужны результаты с высокой точностью, но это также зависит от времени, которое у вас есть на разработку решения, и от того, сколько вы можете на это потратить. Кроме того, ядро ​​радиальной базисной функции обычно обеспечивает более высокую точность, но в некоторых случаях линейное и полиномиальное ядра могут работать одинаково хорошо.

Например, для линейно разделимых данных линейное ядро ​​будет работать так же хорошо, как ядро ​​с радиальным базисом, и при этом потребуется меньше времени на обучение. Поэтому, если ваш набор данных линейно разделим, вам следует выбрать линейное ядро. Для нелинейных данных вы должны выбрать полиномиальную или радиальную базисную функцию в зависимости от времени и затрат, которые у вас есть.

Какие параметры настройки используются с ядрами?

C регуляризация

Параметр регуляризации C принимает значения от вас, чтобы допустить определенный уровень ошибочной классификации в каждом наборе обучающих данных. Более высокие значения регуляризации C приводят к гиперплоскости с малым запасом и не допускают ошибок в классификации. С другой стороны, более низкие значения приводят к высокой марже и большей ошибочной классификации.

Гамма

Параметр гаммы определяет диапазон опорных векторов, которые будут влиять на позиционирование гиперплоскости. Высокое значение гаммы учитывает только близлежащие точки данных, а низкое значение учитывает удаленные точки.

Как реализовать алгоритм машины опорных векторов в Python?

Источник

Поскольку у нас есть основное представление о том, что такое алгоритм SVM и как он работает, давайте углубимся в нечто более сложное. Теперь мы рассмотрим общие шаги по реализации и запуску алгоритма SVM в Python. Мы будем использовать библиотеку Python Scikit-Learn, чтобы узнать, как реализовать алгоритм SVM.

Прежде всего, мы должны импортировать все необходимые библиотеки, такие как Pandas и NumPy, которые необходимы для запуска алгоритмов SVM. Когда у нас есть все библиотеки, мы должны импортировать набор обучающих данных. Далее нам нужно проанализировать наш набор данных. Существует несколько способов анализа набора данных.

Например, мы можем проверить размеры данных, разделить их на ответные и независимые переменные и установить ключевые показатели эффективности для анализа нашего набора данных. После завершения анализа данных мы должны предварительно обработать набор данных. Мы должны проверять наличие нерелевантных, неполных и неправильных данных в нашем наборе данных.

Теперь начинается обучающая часть. Мы должны закодировать и обучить наш алгоритм с соответствующим ядром. Scikit-Learn содержит библиотеку SVM, в которой вы можете найти несколько встроенных классов для обучения алгоритмов. Библиотека SVM содержит класс SVC, который принимает значение для типа ядра, которое вы хотите использовать для обучения своих алгоритмов.

Затем вы вызываете метод подгонки класса SVC, который обучает ваш алгоритм, вставленный в качестве параметра в метод подгонки. Затем вы должны использовать метод прогнозирования класса SVC, чтобы делать прогнозы для алгоритма. После того, как вы завершили шаг прогнозирования, вы должны вызвать классификацию_отчета и путаницу_матрицу библиотеки метрик, чтобы оценить свой алгоритм и увидеть результат.

Каковы приложения алгоритма машины опорных векторов?

Алгоритмы SVM находят применение в различных задачах регрессии и классификации. Некоторые из ключевых применений алгоритмов SVM :

• Классификация текста и гипертекста
• Классификация изображений
• Классификация спутниковых данных, таких как радар с синтезированной апертурой (SAR)
• Классификация биологических веществ, таких как белки
• Распознавание символов в рукописном тексте

Зачем использовать алгоритм опорных векторов?

Алгоритм SVM предлагает различные преимущества, такие как:

• Эффективен при разделении нелинейных данных
• Высокая точность как в более низких, так и в более высоких размерных пространствах
• Невосприимчив к проблеме переобучения, поскольку опорные векторы влияют только на положение гиперплоскости.

Проверьте: 6 типов функций активации в нейронных сетях, которые вам нужно знать

Подводя итоги

В этой статье мы подробно рассмотрели алгоритм машины опорных векторов . Мы узнали об алгоритме SVM , о том, как он работает, его типах, приложениях, преимуществах и реализации на Python. Эта статья даст вам общее представление об алгоритме SVM и ответит на некоторые ваши вопросы.

Но это также вызовет некоторые другие вопросы, например, как алгоритм SVM узнает, какая гиперплоскость правильная, какие другие библиотеки доступны в Python и где найти набор обучающих данных? Если вам интересно узнать больше о машинном обучении, ознакомьтесь с дипломом PG IIIT-B и upGrad в области машинного обучения и искусственного интеллекта, который предназначен для работающих профессионалов и предлагает более 450 часов тщательного обучения, более 30 тематических исследований и заданий, IIIT- Статус B Alumni, 5+ практических проектов и помощь в трудоустройстве в ведущих фирмах.