Python'da Hiyerarşik Kümeleme [Kavramlar ve Analiz]

Ham veri akışının artması ve analiz ihtiyacının artmasıyla birlikte denetimsiz öğrenme kavramı zamanla popüler hale geldi. Etiketli hedef değerleri olmayan girdi verilerinden oluşan veri kümelerinden içgörüler çıkarmak için kullanılır. Python'da hiyerarşik kümelemeyi tartışmaya ve algoritmayı çeşitli veri kümelerine uygulamaya başlamadan önce , kümelemenin temel fikrini tekrar gözden geçirelim.

Kümeleme, temel olarak ham verilerin sınıflandırılması ile ilgilenir. Birbirine en çok benzeyen farklı veri noktalarının birlikte gruplandırılmasını içerir. Bu gruplar, tanımlanan benzerlik veya kümeleme ölçütüne göre oluşturulan kümeler olarak adlandırılır.

Tanıtım

Hiyerarşik kümeleme , bir ağaç veya iyi tanımlanmış bir hiyerarşi biçimindeki verilerle ilgilenir. Süreç, aynı anda iki kümeyle ilgilenmeyi içerir. Algoritma, hesaplama kararları için bir benzerlik veya uzaklık matrisine dayanır. Yani hangi iki kümenin birleştirileceği veya bir kümenin nasıl ikiye bölüneceği. Bu iki seçeneği göz önünde bulundurarak, iki tür hiyerarşik kümelememiz var . Yeni başlayan biriyseniz ve veri bilimi hakkında daha fazla bilgi edinmek istiyorsanız, en iyi üniversitelerden veri bilimi kurslarımıza göz atın.

Algoritmanın kritik yönlerinden biri, tüm algoritma buna dayalı olarak ilerlediğinden benzerlik matrisidir (yakınlık matrisi olarak da bilinir). Makalede daha ayrıntılı olarak tartışılan birçok yakınlık yöntemi vardır.

Türler

Hiyerarşik kümelemenin iki türü vardır:

1. aglomeratif kümeleme
2. Bölücü kümeleme

Türler, temel işlevselliğe göredir: hiyerarşi geliştirme yolu. Aglomeratif aşağıdan yukarıya bir hiyerarşi oluşturucudur, bölücü ise yukarıdan aşağıya bir hiyerarşi oluşturucudur.

Aglomeratif, tüm noktaları ayrı kümeler olarak alır ve ardından bunları her seferinde ikişer olmak üzere her yinelemede birleştirir. Divisive, tüm verileri tek bir küme olarak kabul ederek başlar ve tüm noktalar ayrı kümeler haline gelene kadar böler.

Sonuç, hiyerarşik bir ağaç olarak algılanabilecek bir dizi iç içe kümedir. Bunu görmenin en iyi yolu, hiyerarşiyi görüntülemek için küme yapısını bir dendrograma dönüştürmektir.

Aşağıda küme temsiline karşı basit bir dendrogram örneği verilmektedir:

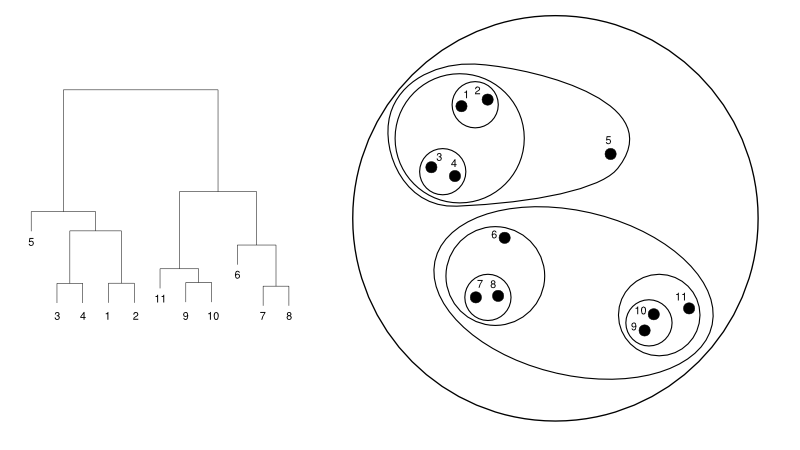
Kaynak

Burada kümeleme her iki şekilde de çalışabilir, ancak sonuç bir kümeler topluluğu olacaktır. 1, 2, 3, 4, 5 ve 6 veri noktaları bir seferde ikiye kümelenir. Ve hiyerarşi oluşumu, aynı dendrogramla ilgilenen soldaki şekilde görülebilir. Aynı analiz, kümelerin kararını anlamada yardımcı olacaktır.

Küme sayısına karar verme

Bu algoritmanın en kullanışlı özelliklerinden biri, algoritma sona erdiğinde istediğiniz kadar küme çıkarabilmenizdir. K-ortalama algoritmasından oldukça farklıdır. K-araçlarında, küme sayısı hiperparametresini geçmemiz gerekir. Bu, algoritma hesaplamayı tamamladığında, o kadar çok kümeye sahip olacağımız anlamına gelir. Ancak daha sonra daha fazla kümeye ihtiyacımız olursa, bunu kolayca ayarlayamayız. Tek seçenek parametreyi değiştirmek ve modeli yeniden eğitmek olacaktır.

Hiyerarşik kümelemeye gelince, küme sayısını daha sonra belirleyebilirsiniz. Sonunda iki küme alabilirsiniz. Memnun kalmazsanız, sondan bir önceki veya daha yüksek seviyedeki adımda oluşturulan beş kümeyi alabilirsiniz. O size bağlı. Bu nedenle, bir kez eğitildikten sonra, daha fazla veya daha az küme elde etmek için modeli yeniden eğitmeniz gerekmez. Dendrogramı istediğiniz seviyede basitçe keserek yapılabilir.

Kavramlar elimizde olduğu için, Python'da hiyerarşik kümelemenin işleyişini tartışalım .

Deney için, kümeleme algoritmaları için sci-kit öğrenme kitaplığını kullanacağız. Ayrıca küme sayısını sınırlamak için "kesme" sürecini görselleştirmek ve anlamak için SciPy'nin cluster.dendrogram modülünü kullanırdık.

numpy'yi np olarak içe aktar

X = np.dizi([[3,5],

[12,9],

[13,17],

[14,14],

[60,52],

[55,63],

[69,59],])

Bir arsa üzerinde böyle bir şey görünecektir:

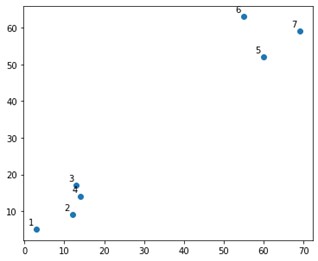
Pekala, üst ve alt köşelerde iki kesin kümemiz olduğunu görüyoruz. Algoritmanın çözüp çözemeyeceğini görelim.

sklearn.clustering modülünden AgglomerativeClustering işlevini kullanıyor olurduk.

sklearn.cluster'dan AglomerativeClustering'i içe aktarın

küme = AglomerativeClustering(n_clusters=2, afinite='euclidean', linkage='ward')

cluster.fit_predict(X)

Burada hiperparametre olmayan kümeleri belirtiyoruz. Ancak, tahmin sınıflarını netleştirmek için onu geçiyoruz. X üzerinden sınıfları tahmin etmenin yanı sıra eğitmek için fit_predict işlevini kullanırdık.

Aglomeratif kümelemenin, yürütülmesi daha basit olduğu için bölücü olmaktan daha fazla kullanıldığını not etmek önemlidir. Yakınlık matrislerine dayalı kümeleri birleştirme fikri, bir kümeyi bir mekanizma yoluyla ikiye bölmekten daha kolay görünüyor.

Okuyun: Python'da Scikit-learn: Özellikler, Ön Koşullar, Artılar ve Eksiler

Yukarıda ne olduğunu açıkça anlamak için algoritmada yer alan adımlara bakın:

Algoritmanın çalışması

Aglomeratif kümelemeyi yürütme adımları şunlardır:

1. Her veri noktasını bir küme olarak tanımlayın
2. İlk yakınlık metriğini hesaplayın
3. Metriğe göre "en yakın" veya benzer olan iki kümeyi birleştirin
4. Yakınlık metriğini gözden geçirin ve tek bir küme kalana kadar üçüncü adımı tekrarlayın.

Dolayısıyla burada anlaşılması gereken tek şey, farklı yakınlık yöntemlerinin etkisidir. Bildiğiniz gibi hiyerarşik kümelemede temel olarak dört tür yakınlık yöntemi vardır. Bu aynı zamanda kümeler arası benzerlik olarak da bilinir.

Yöntemler (veya kodda tanımlandığı gibi bağlantı) şunları içerir:

1. MIN veya Tek bağlantı
2. MAX veya Tam bağlantı
3. Ortalama bağlantı
4. merkez bağlantı
5. Amaç fonksiyonlarının özel fonksiyonları

Bunun sonuçları, dendrogramlar oluşturulurken bağlantı seçeneği uygulanarak kolayca görselleştirilebilir.

Modelin çıktısını görselleştirmek için aşağıdaki gibi küçük bir kod parçacığına ihtiyacımız var:

plt.scatter(X[:,0],X[:,1], c=cluster.labels_, cmap='kış')

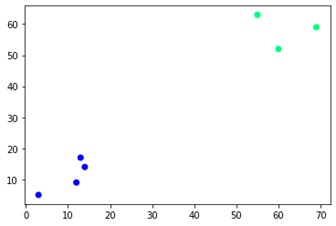
Gördüğünüz gibi karşı köşelerde iki farklı küme var. Küme sayılarıyla da oynayabilir ve farklı sonuçlar görebilirsiniz. Her şey dendrogramları keserek yönlendirilebilir. Bunu anlamak için, dendrogram oluşturmanın görselleştirilmesi için küçük bir pasaj yazalım.

scipy.cluster.hierarchy modülünden dendrogram ve linkage fonksiyonlarını kullanacağız. Burada kullanmak istediğimiz bağlantıyı tanımlıyoruz. Hiyerarşiyi oluşturmak için bu nesneyi dendrogram işlevine geçirmemiz gerekiyor.

scipy.cluster.hierarchy'den dendrogramı içe aktar, bağlantı

bağlantılı = bağlantı(X, 'tamamlandı')

etiketListesi = aralık(1, 8)

plt.şekil(şekil=(10, 7))

dendrogram(bağlı,

oryantasyon='üst',

etiketler=etiketListesi,

mesafe_sort='azalan',

show_leaf_counts=Doğru)

plt.göster()

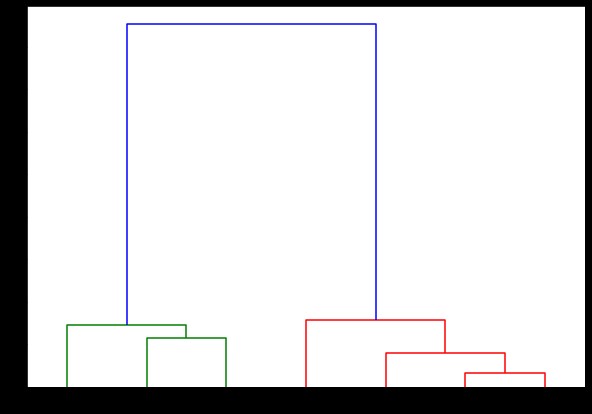
Burada, her yinelemede kümelerin nasıl oluşturulduğunu görselleştirebilirsiniz. Böylece, dendrogramı istediğiniz herhangi bir seviyede kesebilirsiniz ve sonunda o kadar çok küme elde edersiniz. Bu nedenle, bu hiyerarşi oluşturma nedeniyle, algoritma ve verileri yalnızca bir kez çalıştırdıktan sonra küme sayısını değiştirebilirsiniz. Hiyerarşik kümelemeye K-araçları gibi diğer algoritmalar üzerinde bir avantaj sağlayan şeydir.

Şimdi Python'da hiyerarşik kümelemenin yaygın olarak kullanılan bir veri kümesinde nasıl kullanılacağına bakalım : IRIS . Veri setini yerel bir csv'den okuyor olacağız. ve veri kümesinin nasıl göründüğüne ve neyi sınıflandırmamız gerektiğine bir göz atın.

numpy'yi np olarak içe aktar

pandaları pd olarak içe aktar

matplotlib.pyplot'u plt olarak içe aktar

%matplotlib satır içi

veri = pd.read_csv('iris.csv')

veri.kafa()

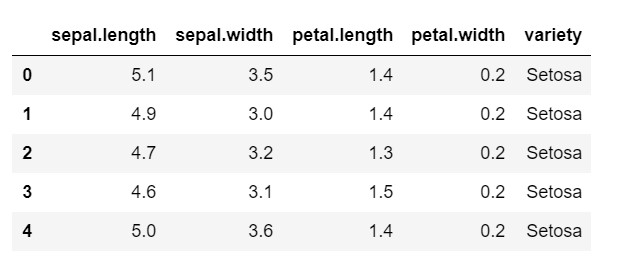
Gördüğünüz gibi, hedef değişken 'variety' sınıfıdır. Bu, model kodlanmış etiketler gerektirdiğinden, sayılara dönüştürülmesi gereken dize biçimindedir. Bunu yapmak için, sklearn'in ön işleme kitaplığındaki etiket kodlayıcıyı kullanıyor olacağız. Onları sayılara dönüştürmek için basit bir uyum ve dönüştürme.

sklearn içe aktarma ön işlemesinden

le = önişleme.LabelEncoder()

le.fit(veri['çeşit'])

veri['çeşit'] = le.transform(veri['çeşit'])

Şimdi bunun üzerinde bir dendrogram oluşturursak çeşitli iterasyonlar ve haritalar buluruz. Tek bir bağlantı ile böyle görünüyor. Aynı kodu kullanır ve tam veya merkez bağlantı ile çalıştırırsak, dendrogramlar biraz farklı olacaktır. Mantık aynı kalır, ancak farklı bağlantılar kesinlikle kümelerin birleşme sırasını etkiler.

scipy.cluster.hierarchy'den dendrogramı içe aktar, bağlantı

bağlantılı = bağlantı(veri, 'koğuş')

plt.şekil(şekil=(10, 7))

dendrogram(bağlı)

plt.göster()

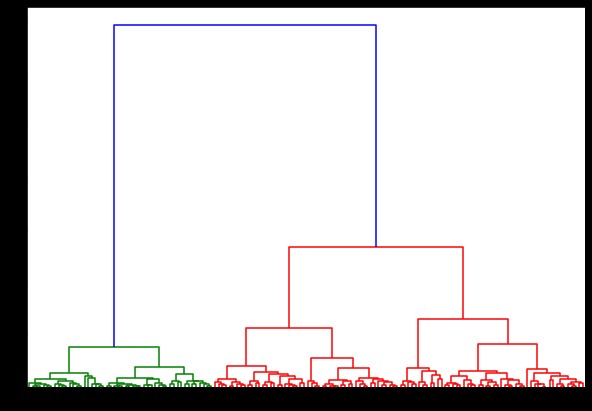
Şimdi, veri kümesine kümeleme uygulayarak, iki farklı bağlantı kullanırdık ve kümeleri tanımlarken gerçekte ne gibi bir fark olduğunu açıkça görürsünüz. Daha önce etiket kodlayıcıdan gördüğümüz gibi 3 farklı sınıfımız var, bu yüzden ilk başta 3 küme uygulayabiliriz.

sklearn.cluster'dan AglomerativeClustering'i içe aktarın

küme = Toplu Kümeleme(n_clusters=3, afinite='öklidyen', bağlantı='tamamlandı')

cluster.fit_predict(veri)

plt.şekil(şekil=(10, 7))

plt.scatter(veri['sepal.length'], veri['petal.length'], c=cluster.labels_)

Yukarıdaki şekilden de görebileceğiniz gibi, 3 kümeli sınıflandırmada bağlantılar, tahminde gözle görülür değişiklikler göstermektedir. Önce koğuş bağlantısına bakın. İki kümede küçük bir değer karışımı olmasına rağmen, yukarıdaki kümeyi tanımlı tutarak etiketleri doğru bir şekilde tahmin eder. Ancak, tam bağlantıyı gördüğümüzde, kümeyi bozar ve bazı değerleri yanlış sınıflandırır.

Yakınlık yöntemlerinde bildiğimiz gibi, yukarıda gördüğümüz gibi, tam bağlantı daha büyük kümeleri kırma eğilimindedir. Koğuş yöntemi veya tek bağlantı yöntemi bu sorunlara karşı daha az savunmasızdır. Bu basit veri kümeleri içindi. Algoritmanın bazı gürültülü veri kümelerinden nasıl etkilendiğini ve bundan nasıl etkilendiğini görelim.

Böyle bir veri kümesi, Pulsar tahmin veri kümesi veya HTRU2 veri kümesidir . Veri seti, yaklaşık 18.000 örnek içerdiğinden daha büyüktür. Bir makine öğrenimi perspektifiyle bakıldığında, veri kümesi oldukça normal boyuttadır, hatta daha da küçüktür. Ancak, karşılaştırmalı olarak, IRIS veri setinden daha ağırdır. Çeşitli bir veri kümesinde uygulama ihtiyacı, Python'da hiyerarşik kümelemenin performansını analiz etmektir . Uygulamaların yollarını ve avantajlarını net bir şekilde anlamak için,

pulsar_data = pd.read_csv('pulsar_stars.csv')

pulsar_data.head()

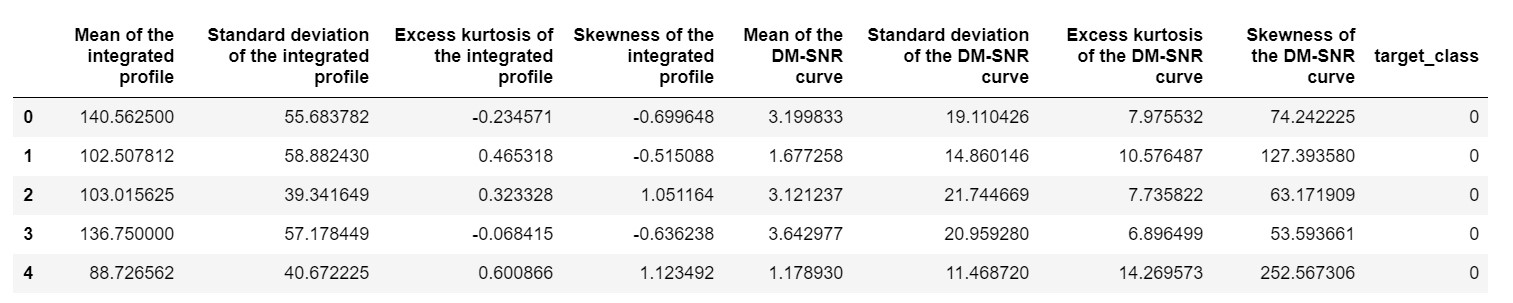
aşırı değerler nedeniyle önyargılı hale gelmemesi için veri setini normalleştirmemiz gerekir.

sklearn.preprocessing'den içe aktarma normalleştirme

pulsar_data = normalize(pulsar_data)

Standart kodu kullanıyor olurduk, ancak bu sefer her iki hesaplamayı da zamanlıyoruz.

%%zaman

scipy.cluster.hierarchy'den dendrogramı içe aktar, bağlantı

bağlantılı = bağlantı(pulsar_data, 'koğuş')

plt.şekil(şekil=(10, 7))

dendrogram(bağlı)

plt.göster()

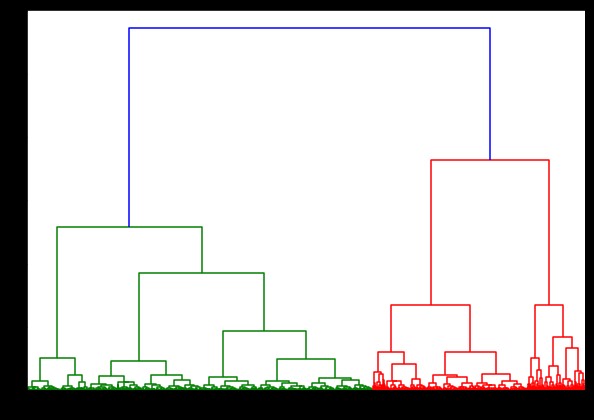
IRIS veri kümesinde bir dendrogram oluşturma zamanlaması 6 saniyeydi. HTRU2 veri kümesinde bir dendrogram oluşturma zamanlaması 13 dakika 54 saniyeydi. Ancak bu, HTRU2 veri kümesiyle eğitilmiş modelde gözlemlediğiniz farklı bağlantılardan kaynaklanan tahminlerdeki değişiklikle karşılaştırıldığında hiçbir şey değildir.

Daha önce yaptığımız işlemin aynısını yapalım. Bu sefer her bağlantı için tahminlerde bulunacaktık.

Aşağıdaki şekil, her bağlantı ile kümeleme tahminlerini göstermektedir:

cluster = AgglomerativeClustering(n_clusters=2, affinity='euclidean', linkage='ortalama') #ve ayrıca tam, koğuş ve tek

cluster.fit_predict(pulsar_data)

plt.şekil(şekil=(10, 7))

plt.scatter(pulsar_data[:,1], pulsar_data[:,7], c=cluster.labels_)

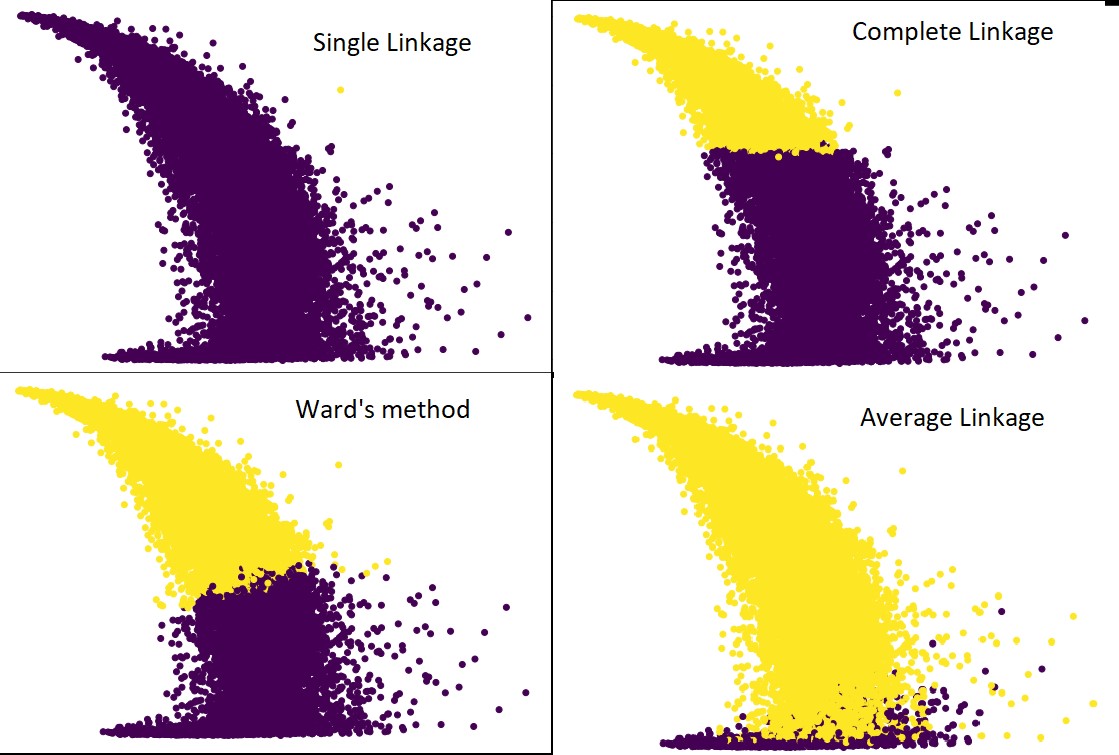
Evet, tahminlerin birbirinden bu kadar farklı olması gerçekten şaşırtıcı. Bu, hiyerarşik kümelemede yakınlık matrisinin önemini göstermektedir.

Gördüğünüz gibi, iki küme arasındaki minimum mesafe yakınlık metriğini tanımladığı için tek bağlantı neredeyse tüm noktaları alır. Bu, onu gürültülü verilere karşı savunmasız hale getirir. Tam bağlantıyı görürsek, verileri kesinlikle iki kümeye ayırır, ancak yakınlığı nedeniyle büyük kümeyi kırmış olabilir.

Ortalama bağlantı, ikisi arasında bir değiş tokuştur. Gürültüden daha az etkilenir, ancak yine de büyük kümeleri kırabilir, ancak daha düşük bir olasılıkla. Ve sınıflandırmayı daha iyi idare eder.

Koğuş yöntemi gibi nesnel işlevler bazen K-ortalamalar gibi diğer kümeleme yöntemlerini başlatmak için kullanılır. Bu yöntem, tıpkı ortalama bağlantı gibi, tek ve tam bağlantı yöntemleri arasında bir ödünleşime sahiptir. Koğuş yöntemi gibi nesnel işlevler, yanlış sınıflandırma olasılığını azaltmak için çoğunlukla özelleştirilmiş çözümlerde kullanılır. Ve iyi performans gösterdiğini görüyoruz.

Öğrenin: Veri Madenciliğinde Küme Analizi: Uygulamalar, Yöntemler ve Gereksinimler

Zaman ve Mekan Karmaşıklığı

Sadece bir anlayış vermek için, yakınlık metriğinin tanımlanma ve hesaplanma şeklini düşünün. Yakınlık metriği, veri haritası içindeki her küme çifti arasındaki mesafeyi depolamayı gerektirir. Alan karmaşıklığını sağlar: O(n2). Bu büyük bir sayıdır. Perspektife koymak için 1.000.000 puanımız olduğunu hayal edin. Bu, alan gereksinimlerini 1012 puana çıkaracaktır. Bir noktanın boyutuna bayt olarak yaklaşarak kaba ve ağır bir ortalama alarak veri boyutunu 1 TB olarak elde ederiz. Ve bunun sabit sürücüde değil, RAM'de saklanması gerekiyor.

İkincisi, zaman karmaşıklığı geliyor. Her iterasyonda yakınlık matrisini tarama ihtiyacı için ve n adım attığımızı düşünürsek, karmaşıklığı O(n3) olarak elde ederiz. Özellikle büyük veri kümelerinde hesaplama açısından pahalıdır.

Onu O(n2logn) düzeyine getirmek mümkün olabilir, ancak yine de K-means gibi diğer kümeleme algoritmalarına kıyasla çok pahalıdır. Algoritmaların uzay ve zaman karmaşıklığını analiz etmek ve maliyet işlevlerini optimize etmek hakkında daha fazla bilgi edinmek istiyorsanız, yukarıGrad'ın Veri Bilimi ve Makine Öğrenimi Programlarına gidebilirsiniz.

sınırlamalar

• İlk sınırlamayı zaten tartışmıştık: Uzay ve zaman karmaşıklığı. Büyük veri kümeleri durumunda hiyerarşik kümelemenin uygun olmadığı açıktır. Zaman karmaşıklığı daha hızlı hesaplamalı makinelerle yönetilse bile, alan karmaşıklığı çok yüksektir. Özellikle RAM'e yüklediğimizde. Ve Python'da hiyerarşik kümelemeyi uyguladığımızda hız sorunu daha da artıyor . Python yavaştır ve büyük görevler söz konusu olduğunda kesinlikle zarar görecektir.
• İkincisi, yakınlık ile optimize edilmiş bir teknik yoktur. Her birinin birden fazla sorunu ve sınırlaması olduğunu görürsek, bu algoritmanın iç mekanizmasını optimize edilmemiş hale getirir.
• Kümeleme kararlarına baktığımızda geri çekilebilir değiller. Anlamı- kümeleme kesin bir yineleme için uygulandıktan sonra, sonlandırılana kadar sonraki yinelemelerde değiştirilmeyecektir. Dolayısıyla, yapısal yanlışlıklar nedeniyle, algoritma herhangi bir noktada birleştirmek veya bölmek için yanlış kümeleri seçerse, bu geri alınamaz.
• Algoritmaya yakından bakarsak, minimize edilmiş net bir amaç fonksiyonumuz yok. Diğer algoritmalarda optimize etmeye çalıştığımız kesin bir fonksiyon vardır. Örneğin, K-araçlarında, hiyerarşik kümelemede durum böyle olmayan, minimize ettiğimiz net bir maliyet fonksiyonumuz vardır.

Kontrol edin: Her Veri Bilimcisinin Bilmesi Gereken En İyi 9 Veri Bilimi Algoritması

Çözüm

Büyük veri kümeleri söz konusu olduğunda belirli sınırlamalar olsa da, bu tür kümeleme algoritması, küçük ila orta ölçekli veri kümeleriyle uğraşırken çekicidir. Python'daki hiyerarşik kümeleme algoritması , endişe verici zaman ve mekan karmaşıklığı ihtiyacı nedeniyle mimaride veya şemada fazla gelişme görmedi.

Ve şu anda Büyük Veri zamanının geldiği doğru. Bu, daha iyi ölçeklenen algoritmalara ihtiyacımız olduğu anlamına gelir. Ancak yine de, küme sayısından emin olmadığımız veya analizi verimli bir şekilde iyileştirmemiz gereken durumlarda, Python'da hiyerarşik kümeleme tatmin edici bir seçim olabilir.

Bununla, artık Python'da hiyerarşik kümelemeyi nasıl uygulayacağınızı biliyorsunuz.

Makine Öğrenimi ve Veri Biliminde bu tür algoritmaları ve yöntemlerin uygulamalarını daha fazla anlamak için upGrad'ın sunduğu kurslara göz atın. İzlemek istediğiniz kariyer yollarından herhangi biri için birikimli programlarımız var.

Programlar, IIIT-B'deki profesörlerin yanı sıra en iyi profesyoneller tarafından küratörlüğünü yapmaktadır. Daha fazla bilgi için upGrad'a gidin . Hızlı teknolojik gelişmelerin önünde olmak için veri bilimi öğrenmeyi merak ediyorsanız, upGrad & IIIT-B'nin Veri Biliminde Yönetici PG Programına göz atın.