Clustering hiérarchique en Python [Concepts et analyse]

Avec l'augmentation du flux de données brutes et le besoin d'analyse, le concept d' apprentissage non supervisé est devenu populaire au fil du temps. Il est utilisé pour tirer des informations à partir d'ensembles de données constitués de données d'entrée sans valeurs cibles étiquetées. Avant de commencer à discuter du clustering hiérarchique en Python et à appliquer l'algorithme sur divers ensembles de données, revoyons l'idée de base du clustering.

Le clustering traite principalement de la classification des données brutes. Il consiste à regrouper différents points de données, qui sont les plus similaires les uns aux autres. Ces groupes sont appelés clusters, qui sont formés en fonction de la métrique de similarité ou de clustering définie.

introduction

Le clustering hiérarchique traite les données sous la forme d'un arbre ou d'une hiérarchie bien définie. Le processus implique de traiter deux clusters à la fois. L'algorithme repose sur une similarité ou une matrice de distance pour les décisions de calcul. Signification, quels deux clusters fusionner ou comment diviser un cluster en deux. Avec ces deux options à l'esprit, nous avons deux types de clustering hiérarchique . Si vous êtes débutant et que vous souhaitez en savoir plus sur la science des données, consultez nos cours de science des données dispensés par les meilleures universités.

L'un des aspects critiques de l'algorithme est la matrice de similarité (également connue sous le nom de matrice de proximité), car l'ensemble de l'algorithme procède en fonction de celle-ci. Il existe de nombreuses méthodes de proximité qui sont abordées plus loin dans l'article.

Les types

Le clustering hiérarchique a deux types :

1. Regroupement agglomératif
2. Regroupement de division

Les types correspondent à la fonctionnalité fondamentale : la manière de développer la hiérarchie. L'agrégation est un générateur de hiérarchie ascendante, tandis que la division est un générateur de hiérarchie descendante.

Agglomerative prend tous les points en tant que clusters individuels, puis les fusionne à chaque itération, deux à la fois. La division commence par supposer que toutes les données sont un cluster et les divise jusqu'à ce que tous les points deviennent des clusters individuels.

Le résultat est un ensemble de clusters imbriqués qui peuvent être perçus comme un arbre hiérarchique. La meilleure façon de l'afficher est de convertir la structure de l'ensemble en un dendrogramme pour afficher la hiérarchie.

Ce qui suit donne un exemple simple d'un dendrogramme par rapport à la représentation en cluster :

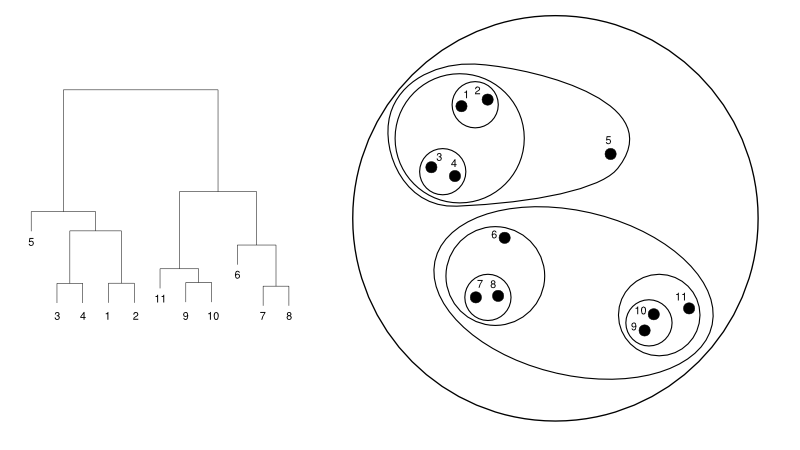
La source

Ici, le clustering peut fonctionner dans les deux sens, mais le résultat sera une collection de clusters. Les points de données 1, 2, 3, 4, 5 et 6 sont regroupés en deux à la fois. Et la formation de la hiérarchie peut être vue dans la figure de gauche, qui traite du dendrogramme de la même chose. La même analyse aiderait à comprendre la décision des clusters.

Décider du nombre de clusters

L'une des fonctionnalités les plus utiles de cet algorithme est que vous pouvez extraire autant de clusters que vous le souhaitez une fois l'algorithme terminé. Il est assez différent de l'algorithme des K-moyennes. Dans K-means, nous devons passer l'hyperparamètre no-of-clusters. Cela signifie qu'une fois que l'algorithme a terminé le calcul, nous aurions autant de clusters. Mais, si nous avons besoin de plus de clusters plus tard, nous ne pouvons pas régler aussi facilement. La seule option serait de modifier le paramètre et d'entraîner à nouveau le modèle.

Alors qu'en ce qui concerne le clustering hiérarchique, vous pouvez définir le nombre de clusters ultérieurement. Vous pouvez prendre deux grappes à la fin. Si vous n'êtes pas satisfait, vous pouvez prendre les cinq groupes formés à l'avant-dernière étape ou au niveau supérieur. Cela dépend de toi. Par conséquent, une fois formé, vous n'avez pas besoin de recycler le modèle pour obtenir plus ou moins de clusters. Cela peut être accompli en coupant simplement le dendrogramme au niveau que vous désirez.

Comme nous avons les concepts en place, discutons du fonctionnement du clustering hiérarchique en Python .

Pour l'expérience, nous allons utiliser la bibliothèque sci-kit learn pour les algorithmes de clustering. Nous utiliserions également le module cluster.dendrogram de SciPy pour visualiser et comprendre le processus de "coupe" pour limiter le nombre de clusters.

importer numpy en tant que np

X = np.tableau([[3,5],

[12,9],

[13,17],

[14,14],

[60,52],

[55,63],

[69,59],])

Cela ressemblerait à ceci sur une parcelle:

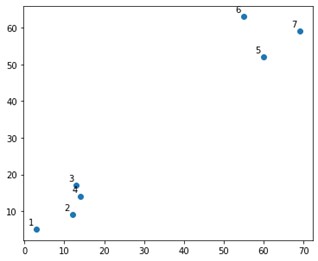
Eh bien, nous voyons que nous avons deux groupes définitifs, dans les coins supérieur et inférieur. Voyons si l'algorithme peut le comprendre ou non.

Nous utiliserions la fonction AgglomerativeClustering du module sklearn.clustering.

depuis sklearn.cluster import AgglomerativeClustering

cluster = AgglomerativeClustering(n_clusters=2, affinity='euclidean', link='ward')

cluster.fit_predict(X)

Ici, nous spécifions les clusters, qui ne sont pas un hyperparamètre. Cependant, nous le passons simplement pour clarifier les classes de prédiction. Nous utiliserions la fonction fit_predict pour entraîner et prédire les classes sur X.

Il est important de noter que le clustering agglomératif est plus utilisé que diviseur car il est plus simple à exécuter. L'idée de fusionner des clusters basés sur des matrices de proximité semble plus facile que de diviser un cluster en deux via un mécanisme.

Lire : Scikit-learn en Python : fonctionnalités, prérequis, avantages et inconvénients

Pour bien comprendre ce qui s'est passé ci-dessus, regardez les étapes impliquées dans l'algorithme :

Fonctionnement de l'algorithme

Voici les étapes pour exécuter le clustering agglomératif :

1. Définir chaque point de données en tant que cluster
2. Calculer la métrique de proximité initiale
3. Fusionner deux clusters qui sont les "plus proches" ou similaires en fonction de la métrique
4. Révisez la métrique de proximité et répétez la troisième étape jusqu'à ce qu'il ne reste qu'un seul cluster.

Il ne reste donc ici qu'à comprendre l'impact des différentes méthodes de proximité. Comme vous le savez, il existe principalement quatre types de méthodes de proximité dans le clustering hiérarchique. Ceci est également connu sous le nom de similarité inter-cluster.

Les méthodes (ou liaisons, telles que définies dans le code) incluent :

1. MIN ou attelage simple
2. Liaison MAX ou Complète
3. Liaison moyenne
4. Liaison centroïde
5. Fonctions exclusives des fonctions objectifs

Les résultats peuvent être facilement visualisés en appliquant l'option de liaison lors de la création des dendrogrammes.

Pour visualiser la sortie du modèle, nous avons juste besoin d'un petit extrait de code comme suit :

plt.scatter(X[:,0],X[:,1], c=cluster.labels_, cmap='hiver')

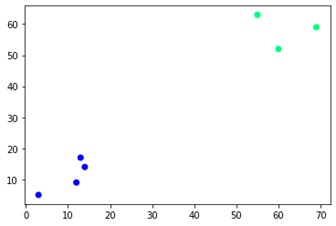
Comme vous pouvez le voir, il y a deux clusters différents sur les coins opposés. Vous pouvez aussi jouer avec les numéros de cluster et voir des résultats différents. Le tout peut être piloté en coupant des dendrogrammes. Pour comprendre cela, écrivons un petit extrait pour la visualisation de la création de dendrogrammes.

Nous allons utiliser les fonctions de dendrogramme et de liaison du module scipy.cluster.hierarchy. Ici, nous définissons le lien que nous voulons utiliser. Nous devons transmettre cet objet à la fonction dendrogramme pour générer la hiérarchie.

de scipy.cluster.hierarchy import dendrogramme, liaison

lié = lien (X, 'complet')

étiquetteListe = plage (1, 8)

plt.figure(figsize=(10, 7))

dendrogramme(lié,

orientation='top',

étiquettes=listeétiquettes,

distance_sort='décroissant',

show_leaf_counts=Vrai)

plt.show()

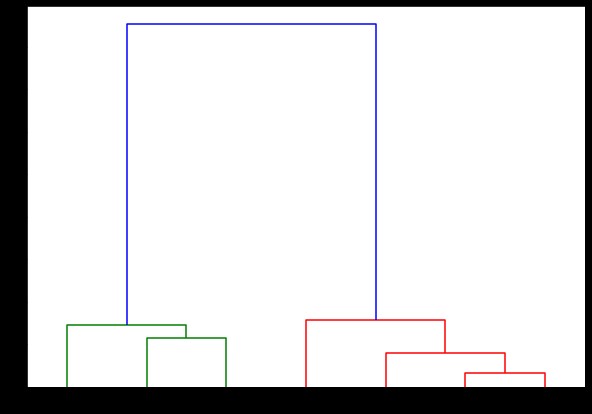
Ici, vous pouvez visualiser comment les clusters sont formés à chaque itération. Ainsi, vous pouvez couper le dendrogramme à n'importe quel niveau que vous voulez, et vous vous retrouveriez avec autant de clusters. Par conséquent, en raison de la création de cette hiérarchie, vous pouvez faire varier le nombre de clusters après une seule analyse de l'algorithme et des données. C'est ce qui donne au clustering hiérarchique un avantage sur d'autres algorithmes comme K-means.

Voyons maintenant comment utiliser le clustering hiérarchique en Python sur un ensemble de données couramment utilisé : IRIS . Nous serions en train de lire l'ensemble de données à partir d'un csv local. et jetez simplement un coup d'œil à l'apparence de l'ensemble de données et à ce que nous devons classer.

importer numpy en tant que np

importer des pandas en tant que pd

importer matplotlib.pyplot en tant que plt

%matplotlib en ligne

données = pd.read_csv('iris.csv')

data.head()

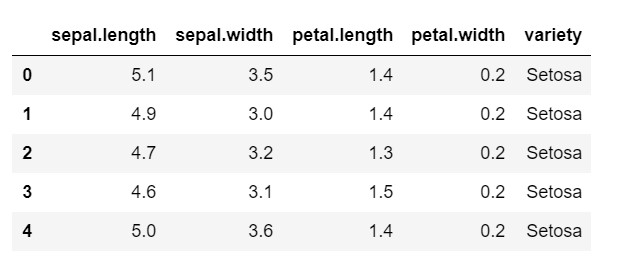
Comme vous pouvez le voir, la variable cible est la classe 'variété'. Il s'agit d'un format de chaîne qui doit être converti en nombres, car le modèle nécessite des étiquettes codées. Pour ce faire, nous utiliserions l'encodeur d'étiquettes de la bibliothèque de prétraitement de sklearn. Un simple ajustement et transformation pour les convertir en nombres.

du prétraitement d'importation sklearn

le = preprocessing.LabelEncoder()

le.fit(data['variété'])

data['variété'] = le.transform(data['variété'])

Maintenant, si nous créons un dendrogramme là-dessus, nous trouvons diverses itérations et cartes. Voici à quoi cela ressemble avec un seul lien. Si nous utilisons le même code et l'exécutons avec une liaison complète ou centroïde, les dendrogrammes différeraient un peu. La logique reste la même, mais des liens différents affecteraient certainement l'ordre de fusion des clusters.

de scipy.cluster.hierarchy import dendrogramme, liaison

lié = lien (données, 'quartier')

plt.figure(figsize=(10, 7))

dendrogramme (lié)

plt.show()

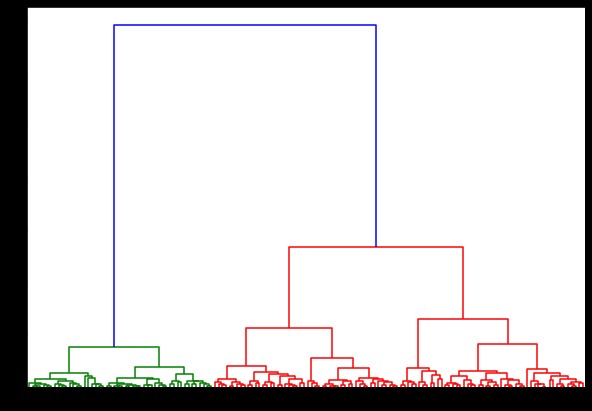
Maintenant, en appliquant le clustering sur l'ensemble de données, nous utiliserions deux liens différents, et vous verriez clairement quelle différence cela a vraiment lors de la définition des clusters. Comme nous l'avons déjà vu à partir de l'encodeur d'étiquettes, nous avons 3 classes différentes, nous pouvons donc appliquer 3 clusters dans un premier temps.

depuis sklearn.cluster import AgglomerativeClustering

cluster = AgglomerativeClustering(n_clusters=3, affinity='euclidean', link='complete')

cluster.fit_predict(données)

plt.figure(figsize=(10, 7))

plt.scatter(data['sepal.length'], data['petal.length'], c=cluster.labels_)

Comme vous pouvez le voir sur la figure ci-dessus, dans la classification en 3 groupes, les liens montrent des changements visibles dans la prédiction. Regardez d'abord le lien de service. Il prédit correctement les étiquettes en gardant le cluster ci-dessus défini, même s'il y a un petit mélange de valeurs dans les deux clusters. Mais, lorsque nous voyons le lien complet, il décompose le cluster et classe mal certaines des valeurs.

Comme nous le savons dans les méthodes de proximité, la liaison complète a tendance à briser les plus grands clusters, comme nous pouvons le voir ci-dessus. La méthode du service ou la méthode de liaison unique est moins vulnérable à ces problèmes. C'était pour les ensembles de données simples. Voyons comment l'algorithme souffre et est affecté par certains ensembles de données bruités.

L'un de ces ensembles de données est l'ensemble de données de prédiction Pulsar ou l'ensemble de données HTRU2 . L'ensemble de données est plus grand, car il contient environ 18 000 échantillons. S'il est vu dans une perspective ML, l'ensemble de données est de taille assez régulière, voire inférieure. Mais, comparativement, il est plus lourd que le jeu de données IRIS. Le besoin d'implémentation sur un jeu de données varié est d'analyser les performances du clustering hiérarchique en Python . Pour bien comprendre les modalités et les avantages des implémentations,

pulsar_data = pd.read_csv('pulsar_stars.csv')

pulsar_data.head()

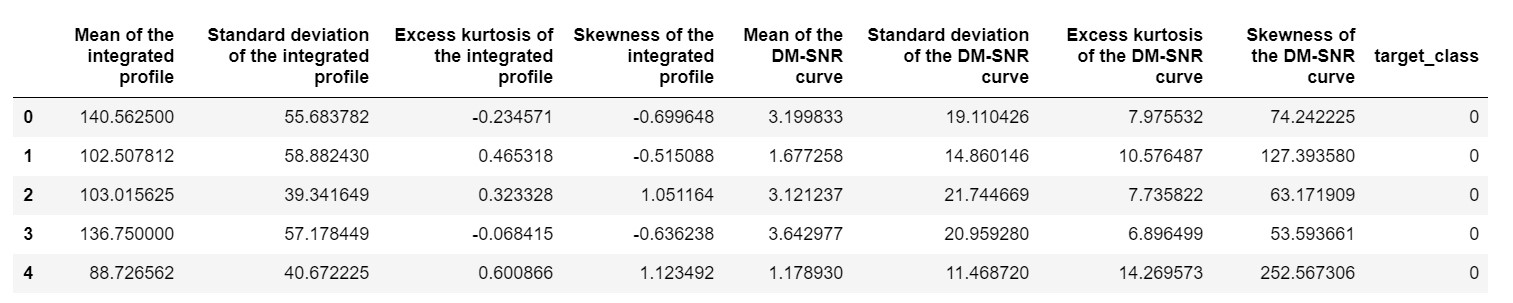
nous aurions besoin de normaliser l'ensemble de données afin qu'il ne soit pas biaisé en raison de valeurs extrêmes.

de sklearn.preprocessing importer normaliser

pulsar_data = normaliser(pulsar_data)

Nous utiliserions le code standard, mais cette fois, nous chronométrons les deux calculs.

%%temps

de scipy.cluster.hierarchy import dendrogramme, liaison

lié = lien (pulsar_data, 'ward')

plt.figure(figsize=(10, 7))

dendrogramme (lié)

plt.show()

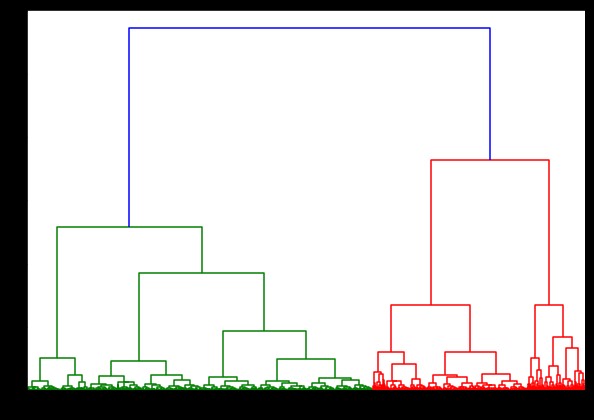
Le temps de génération d'un dendrogramme sur l'ensemble de données IRIS était de 6 secondes. Le temps de génération d'un dendrogramme sur l'ensemble de données HTRU2 était de 13 min 54 secondes. Mais ce n'est rien comparé au changement des prédictions dû aux différentes liaisons, que vous observez dans le modèle formé avec l'ensemble de données HTRU2.

Suivons la même procédure que précédemment. Cette fois, nous ferions des prédictions sur chaque liaison.

La figure suivante montre les prédictions de clustering avec chaque liaison :

cluster = AgglomerativeClustering(n_clusters=2, affinity='euclidean', link='average') #ainsi que complete,ward et single

cluster.fit_predict(pulsar_data)

plt.figure(figsize=(10, 7))

plt.scatter(pulsar_data[:,1], pulsar_data[:,7], c=cluster.labels_)

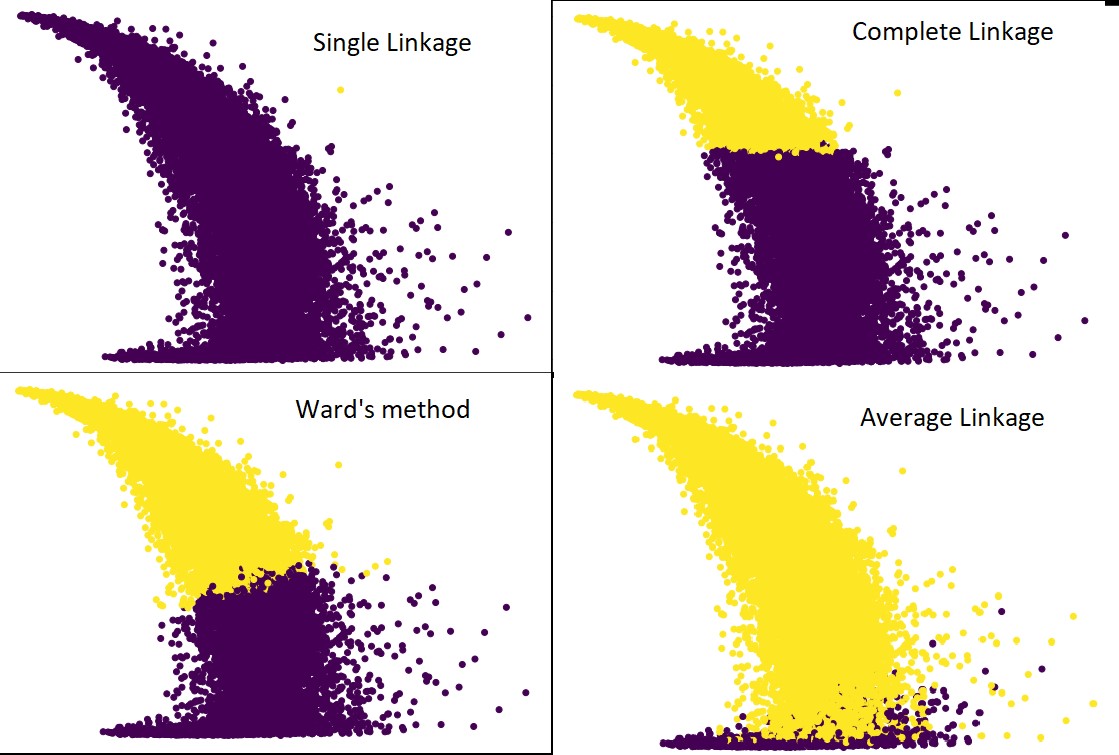
Oui, il est en effet surprenant de constater à quel point les prédictions diffèrent les unes des autres. Cela montre l'importance de la matrice de proximité dans le clustering hiérarchique.

Comme vous pouvez le voir, la liaison unique prend en compte presque tous les points car la distance minimale entre deux clusters définit la métrique de proximité. Cela le rend vulnérable aux données bruyantes. Si nous voyons le lien complet, il divise définitivement les données en deux groupes, mais il peut avoir rompu le grand groupe simplement en raison de sa proximité.

Le lien moyen est un compromis entre les deux. Il est moins affecté par le bruit, mais il peut toujours casser de gros amas, mais avec une moindre probabilité. Et, il gère mieux la classification.

Des fonctions objectives comme la méthode de la salle sont parfois utilisées pour initialiser d'autres méthodes de regroupement comme K-means. Cette méthode, tout comme le couplage moyen, a un compromis entre les méthodes de couplage simple et complet. Les fonctions objectives telles que la méthode de la salle sont principalement utilisées dans des solutions personnalisées pour réduire la probabilité d'erreur de classification. Et, nous le voyons bien fonctionner.

Apprendre : Analyse de grappes dans l'exploration de données : applications, méthodes et exigences

Complexité temporelle et spatiale

Juste pour comprendre, considérez la façon dont la métrique de proximité est définie et calculée. La métrique de proximité nécessite de stocker la distance entre chaque paire de clusters à l'intérieur de la carte de données. Cela donne une complexité spatiale : O(n2). C'est un grand nombre. Pour mettre les choses en perspective, imaginons que nous ayons 1 000 000 points. Cela portera l'espace requis à 1012 points. En prenant une moyenne approximative et lourde en approchant la taille d'un point comme un octet, nous obtenons la taille des données à 1 To. Et cela doit être stocké dans la RAM, pas sur le disque dur.

Deuxièmement, vient la complexité temporelle. Pour le besoin de scanner la matrice de proximité à chaque itération et en considérant que l'on prend n pas, on obtient la complexité en O(n3). Il est coûteux en calcul, en particulier sur les grands ensembles de données.

Il est peut-être possible de le ramener à O(n2logn), mais cela reste trop cher par rapport à d'autres algorithmes de clustering, comme K-means. Si vous souhaitez en savoir plus sur l'analyse de la complexité spatiale et temporelle des algorithmes et sur l'optimisation des fonctions de coût, vous pouvez vous diriger vers les programmes upGrad en science des données et en apprentissage automatique.

Limites

• Nous avons déjà évoqué la première limitation : la complexité spatiale et temporelle. Il est évident que le clustering hiérarchique n'est pas favorable dans le cas de grands ensembles de données. Même si la complexité temporelle est gérée avec des machines de calcul plus rapides, la complexité spatiale est trop élevée. Surtout quand on le charge dans la RAM. Et, le problème de la vitesse augmente encore plus lorsque nous implémentons le clustering hiérarchique en Python. Python est lent, et si de grosses tâches sont concernées, il en souffrira certainement.
• Deuxièmement, il n'y a pas de technique optimisée avec la proximité. Si nous voyons que chacun a de multiples problèmes et limitations, cela rend le mécanisme interne de l'algorithme non optimisé.
• Quand on regarde les décisions de regroupement, elles ne sont pas rétractables. Ce qui signifie qu'une fois que le regroupement a été appliqué pour une itération définie, il ne sera pas modifié dans d'autres itérations jusqu'à la fin. Ainsi, si en raison d'inexactitudes structurelles, l'algorithme, à tout moment, choisit de mauvais clusters à combiner ou à diviser, il est irrévocable.
• Si nous examinons de près l'algorithme, nous n'avons pas de fonction objectif claire qui est minimisée. Dans d'autres algorithmes, il y a une fonction définie que nous essayons d'optimiser. Par exemple, dans K-means nous avons une fonction de coût claire que nous minimisons, ce qui n'est pas le cas avec le clustering hiérarchique.

Découvrez : Top 9 des algorithmes de science des données que tout scientifique de données devrait connaître

Conclusion

Même s'il existe certaines limites en ce qui concerne les grands ensembles de données, ce type d'algorithme de clustering est attrayant lorsqu'il s'agit d'ensembles de données à petite et moyenne échelle. L' algorithme de clustering hiérarchique en Python n'a pas connu beaucoup de développement dans l'architecture ou le schéma en raison de son besoin alarmant de complexité temporelle et spatiale.

Et, il est vrai qu'en ce moment, l'heure est au Big Data. Cela signifie que nous avons besoin d'algorithmes qui évoluent mieux. Mais, encore, dans les cas où nous ne sommes pas sûrs du nombre de clusters, ou nous devons affiner l'analyse efficacement, le clustering hiérarchique en Python peut être un choix satisfaisant.

Avec cela, vous savez maintenant comment implémenter le clustering hiérarchique en Python.

Pour mieux comprendre ces algorithmes et applications de méthodes en apprentissage automatique et en science des données, consultez les offres de cours d'upGrad. Nous avons des programmes cumulatifs pour tous les cheminements de carrière que vous souhaitez suivre.

Les programmes sont organisés par les meilleurs professionnels ainsi que les professeurs de l'IIIT-B. Pour plus d'informations, rendez-vous sur upGrad . Si vous êtes curieux d'apprendre la science des données pour être à l'avant-garde des avancées technologiques rapides, consultez le programme exécutif PG de upGrad & IIIT-B en science des données.