Python中的层次聚类【概念与分析】

随着原始数据流量的增加和分析需求的增加，无监督学习的概念随着时间的推移变得流行起来。 它用于从由没有标记目标值的输入数据组成的数据集中得出见解。 在我们开始讨论Python 中的层次聚类并将算法应用于各种数据集之前，让我们重温一下聚类的基本思想。

聚类主要处理原始数据的分类。 它包括将彼此最相似的不同数据点组合在一起。 这些组称为集群，它们是根据定义的相似性或聚类度量形成的。

介绍

层次聚类以树或定义明确的层次结构的形式处理数据。 该过程涉及一次处理两个集群。 该算法依赖于相似度或距离矩阵来进行计算决策。 含义，要合并哪两个集群或如何将集群分成两个。 考虑到这两个选项，我们有两种类型的层次聚类。 如果您是初学者并且有兴趣了解有关数据科学的更多信息，请查看我们来自顶尖大学的数据科学课程。

该算法的关键方面之一是相似度矩阵（也称为邻近矩阵），因为整个算法都基于它进行。 本文将进一步讨论许多邻近方法。

类型

层次聚类有两种类型：

1. 凝聚聚类
2. 分裂聚类

这些类型是基于基本功能的：开发层次结构的方式。 Agglomerative 是一个自下而上的层次结构生成器，而 Divisive 是一个自上而下的层次结构生成器。

Agglomerative 将所有点作为单独的集群，然后在每次迭代中合并它们，一次两个。 Divisive 首先将整个数据假设为一个集群，然后将其划分，直到所有点都成为单独的集群。

结果是一组嵌套集群，可以被视为层次树。 查看它的最佳方法是将集合结构转换为树状图以查看层次结构。

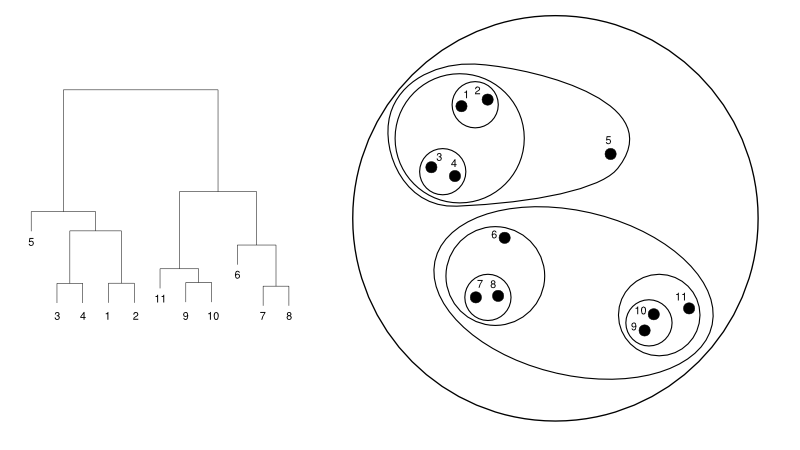
下面给出了一个树状图与集群表示的简单示例：

资源

在这里，聚类可能会以任何一种方式工作，但结果将是一个集群的集合。 数据点 1、2、3、4、5 和 6 一次聚集成两个。 并且层次结构可以在左图中看到，它处理相同的树状图。 相同的分析将有助于理解集群的决策。

确定集群的数量

该算法最有用的功能之一是，一旦算法终止，您可以提取任意数量的集群。 它与 K-means 算法完全不同。 在 K-means 中，我们需要传递 no-of-clusters 超参数。 这意味着一旦算法完成计算，我们就会拥有那么多集群。 但是，如果我们以后需要更多的集群，我们就不能轻易地进行调整。 唯一的选择是更改参数并再次训练模型。

然而，当涉及到层次聚类时，您可以稍后设置聚类的数量。 最后你可以拿两个集群。 如果不满意，您可以采取倒数第二级或更高级别形成的五个集群。 这取决于你。 因此，一旦经过训练，您无需重新训练模型即可获得更多或更少的集群。 它可以通过简单地将树状图切割到您想要的水平来完成。

了解了概念后，让我们讨论一下Python 中层次聚类的工作原理。

在实验中，我们将使用 sci-kit learn 库进行聚类算法。 我们还将使用 SciPy 的 cluster.dendrogram 模块来可视化和理解限制集群数量的“切割”过程。

将 numpy 导入为 np

X = np.array([[3,5],

[12,9],

[13,17]，

[14,14]，

[60,52],

[55,63],

[69,59],])

在情节上看起来像这样：

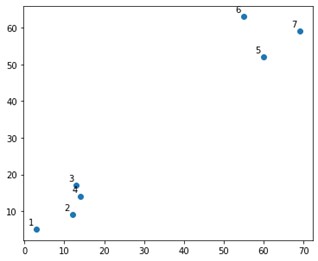
好吧，我们确实看到我们有两个确定的集群，在顶角和底角。 让我们看看算法是否可以解决这个问题。

我们将使用 sklearn.clustering 模块中的 AgglomerativeClustering 函数。

从 sklearn.cluster 导入 AgglomerativeClustering

cluster = AgglomerativeClustering（n_clusters=2，affinity='euclidean'，linkage='ward'）

cluster.fit_predict(X)

在这里，我们确实指定了集群，这不是超参数。 但是，我们只是传递它以使预测类别清晰。 我们将使用 fit_predict 函数来训练和预测 X 上的类。

需要注意的是，凝聚聚类比分裂聚类更常用，因为它更易于执行。 基于邻近矩阵合并集群的想法似乎比通过某种机制将集群分成两个更容易。

阅读： Python 中的 Scikit-learn：功能、先决条件、优缺点

为了清楚地理解上面发生了什么，看一下算法中涉及的步骤：

算法的工作

以下是执行凝聚聚类的步骤：

1. 将每个数据点定义为一个集群
2. 计算初始接近度指标
3. 根据指标合并两个“最接近”或相似的集群
4. 修改邻近度指标并重复第三步，直到剩下一个集群。

因此，这里唯一需要了解的是不同邻近方法的影响。 如您所知，层次聚类中主要有四种邻近方法。 这也称为集群间相似性。

方法（或代码中定义的链接）包括：

1. MIN 或单联动
2. MAX 或完全联动
3. 平均联动
4. 质心连杆
5. 目标函数的独占函数

通过在创建树状图时应用链接选项，可以轻松地可视化相同的结果。

为了可视化模型的输出，我们只需要一个小代码片段，如下所示：

plt.scatter(X[:,0],X[:,1], c=cluster.labels_, cmap='winter')

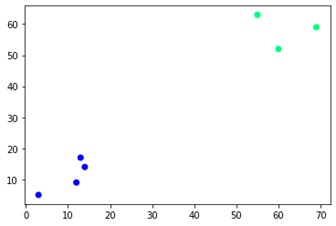
如您所见，对角有两个不同的集群。 你也可以玩弄簇号并看到不同的结果。 整个事情可以通过切割树状图来驱动。 为了理解这一点，让我们为树状图创建的可视化编写一个小片段。

我们将使用 scipy.cluster.hierarchy 模块中的树状图和链接函数。 在这里，我们定义了我们想要使用的链接。 我们需要将该对象传递给 dendrogram 函数以生成层次结构。

从 scipy.cluster.hierarchy 导入树状图，链接

链接=链接（X，'完成'）

标签列表 = 范围 (1, 8)

plt.figure(figsize=(10, 7))

树状图（链接，

方向='顶部'，

标签=标签列表，

distance_sort='降序',

show_leaf_counts=真）

plt.show()

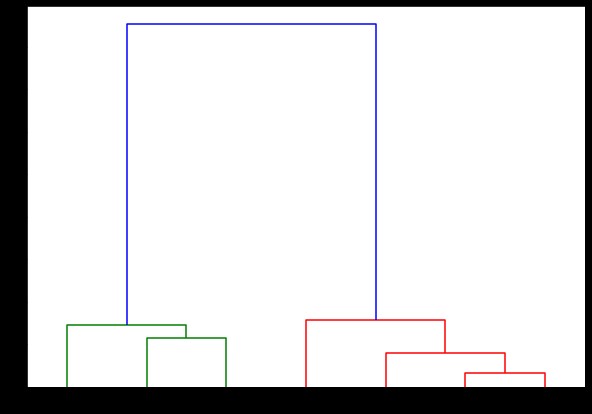
在这里，您可以可视化每次迭代时集群是如何形成的。 所以，你可以在任何你想要的层次上切割树状图，你最终会得到那么多簇。 因此，由于这种层次结构的创建，您可能会在仅运行一次算法和数据后改变集群的数量。 它使层次聚类在其他算法（如 K-means）上具有优势。

现在，让我们看看如何在 Python中对常用数据集IRIS使用层次聚类。 我们将从本地 csv 读取数据集。 只需看一下数据集的外观以及我们需要分类的内容。

将 numpy 导入为 np

将熊猫导入为 pd

将 matplotlib.pyplot 导入为 plt

%matplotlib 内联

数据 = pd.read_csv('iris.csv')

数据头（）

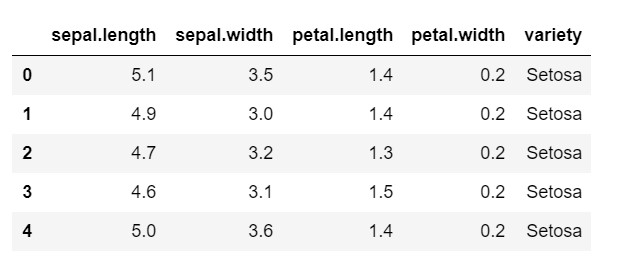
如您所见，目标变量是“品种”类。 这是字符串格式，需要转换为数字，因为模型需要编码标签。 为此，我们将使用 sklearn 预处理库中的标签编码器。 一个简单的拟合和变换将它们转换成数字。

从 sklearn 导入预处理

le = preprocessing.LabelEncoder()

le.fit(数据['品种'])

数据['品种'] = le.transform(数据['品种'])

现在，如果我们在此基础上创建一个树状图，我们会发现各种迭代和映射。 这是使用单个链接的外观。 如果我们使用相同的代码并使用完整或质心链接运行它，则树状图会有所不同。 逻辑是一样的，但不同的联系肯定会影响集群合并的顺序。

从 scipy.cluster.hierarchy 导入树状图，链接

链接=链接（数据，“病房”）

plt.figure(figsize=(10, 7))

树状图（链接）

plt.show()

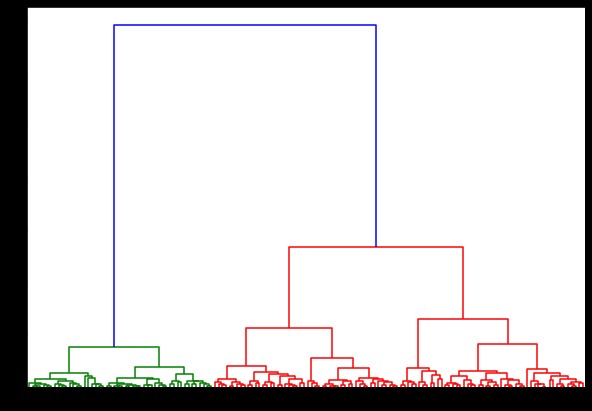
现在，在数据集上应用聚类，我们将使用两个不同的链接，您会清楚地看到它在定义聚类时真正有什么不同。 正如我们已经从标签编码器中看到的那样，我们有 3 个不同的类，所以我们可能首先应用 3 个集群。

从 sklearn.cluster 导入 AgglomerativeClustering

cluster = AgglomerativeClustering（n_clusters=3，affinity='euclidean'，linkage='complete'）

cluster.fit_predict（数据）

plt.figure(figsize=(10, 7))

plt.scatter(data['sepal.length'], data['petal.length'], c=cluster.labels_)

从上图中可以看出，在 3-cluster 分类中，链接显示预测的可见变化。 先看病房联动。 它通过保持上述集群的定义来正确预测标签，即使两个集群中的值有少量混合。 但是，当我们看到完整的链接时，它会破坏集群并错误分类一些值。

正如我们在邻近方法中所知道的，完整的链接确实倾向于破坏较大的集群，正如我们在上面看到的。 病房法或单一联动法不易受这些问题的影响。 这是针对简单数据集的。 让我们看看算法如何受到一些嘈杂数据集的影响和影响。

一个这样的数据集是 Pulsar 预测数据集或HTRU2 数据集。 数据集更大，因为它包含大约 18,000 个样本。 如果从 ML 的角度来看，数据集的大小相当规则，甚至更小。 但是，相对而言，它比 IRIS 数据集更重。 在不同数据集上实现的需要是分析Python 中层次聚类的性能。 为了清楚地了解实施的方式和好处，

pulsar_data = pd.read_csv('pulsar_stars.csv')

pulsar_data.head()

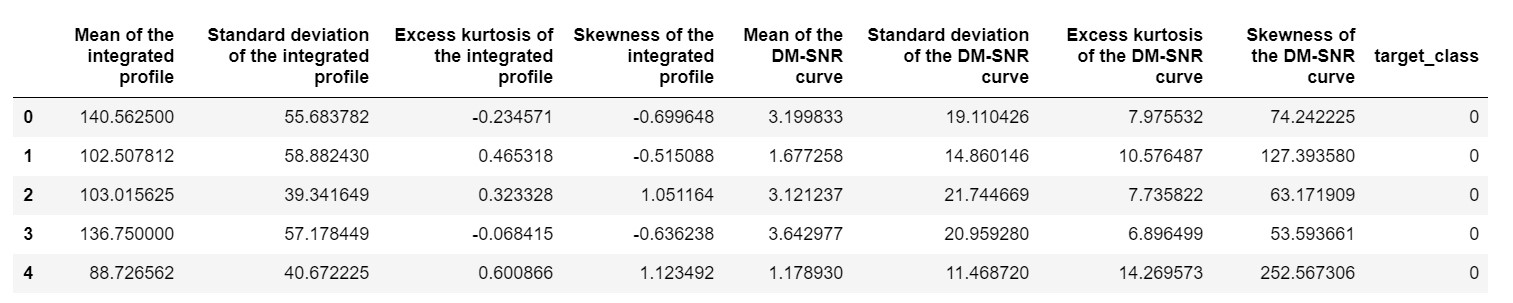
我们需要对数据集进行标准化，使其不会因极端值而出现偏差。

从 sklearn.preprocessing 导入规范化

pulsar_data = 标准化（pulsar_data）

我们将使用标准代码，但这一次，我们对两个计算进行计时。

％％时间

从 scipy.cluster.hierarchy 导入树状图，链接

链接=链接（pulsar_data，“病房”）

plt.figure(figsize=(10, 7))

树状图（链接）

plt.show()

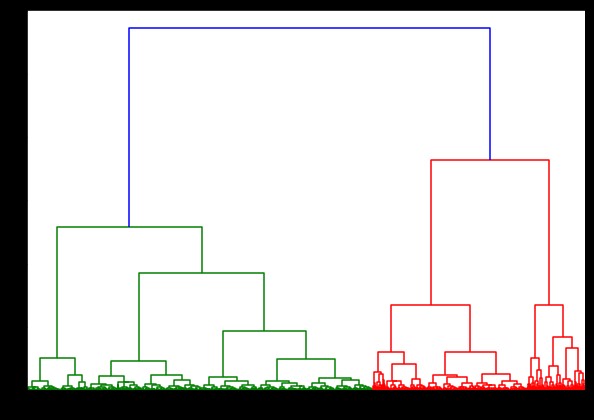
在 IRIS 数据集上生成树状图的时间为 6 秒。 在 HTRU2 数据集上生成树状图的时间为 13 分 54 秒。 但是，与您在使用 HTRU2 数据集训练的模型中观察到的不同链接导致的预测变化相比，这算不了什么。

让我们遵循与之前相同的程序。 这一次，我们将对每一个联系做出预测。

下图显示了每个链接的聚类预测：

cluster = AgglomerativeClustering(n_clusters=2, affinity='euclidean', links='average') #as well as complete,ward and single

cluster.fit_predict(pulsar_data)

plt.figure(figsize=(10, 7))

plt.scatter(pulsar_data[:,1], pulsar_data[:,7], c=cluster.labels_)

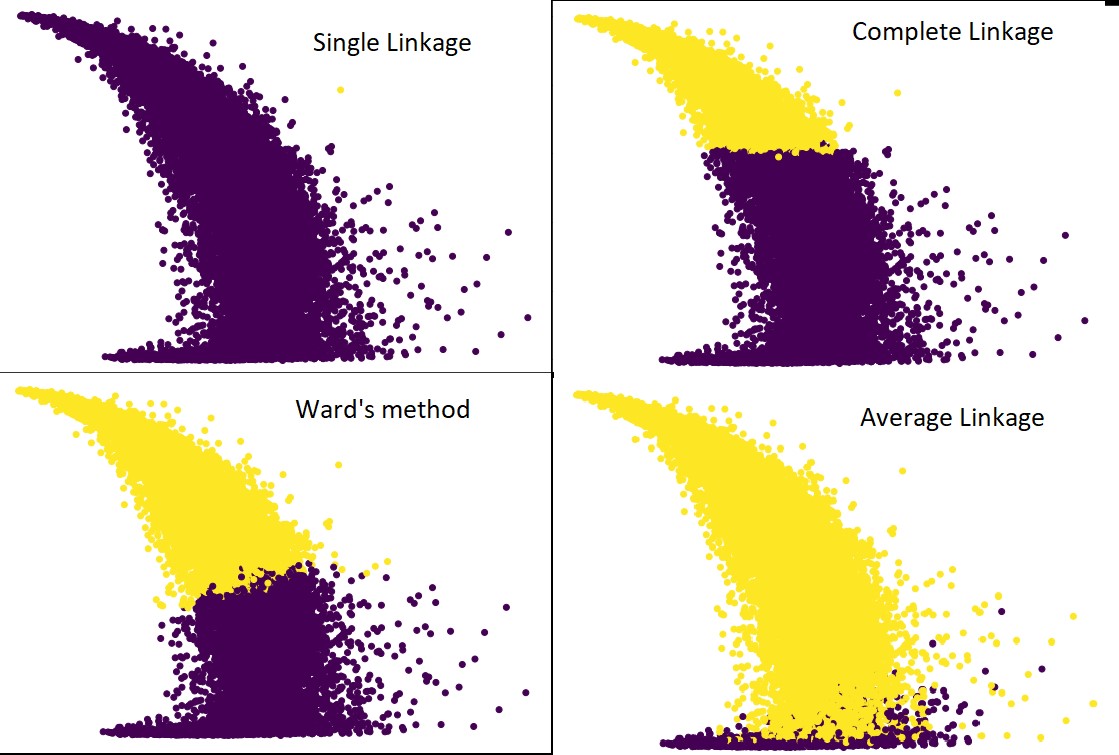
是的，这些预测之间的差异确实令人惊讶。 这表明了邻近矩阵在层次聚类中的重要性。

如您所见，单个链接几乎包含所有点，因为两个集群之间的最小距离定义了邻近度度量。 这使得它容易受到嘈杂数据的影响。 如果我们看到完整的链接，它肯定会将数据分成两个集群，但它可能仅仅因为它的接近而破坏了大集群。

平均联系是两者之间的权衡。 它受噪声影响较小，但仍可能破坏大型集群，但概率较小。 而且，它确实可以更好地处理分类。

像沃德方法这样的目标函数有时用于初始化其他聚类方法，如 K-means。 这种方法，就像平均联动一样，在单一和完全联动方法之间进行权衡。 像ward's method这样的目标函数主要用于定制解决方案，以减少错误分类的可能性。 而且，我们确实看到它表现良好。

学习：数据挖掘中的聚类分析：应用、方法和要求

时间和空间复杂度

为了便于理解，请考虑定义和计算邻近度指标的方式。 邻近度度量需要存储数据图中每对集群之间的距离。 它使空间复杂度：O(n2)。 这是一个很大的数字。 换个角度来看，假设我们有 1,000,000 个点。 这将使空间要求达到 1012 点。 通过将一个点的大小近似为一个字节来粗略地取平均值，我们得到的数据大小为 1TB。 这需要存储在 RAM 中，而不是硬盘上。

其次，时间复杂度。 由于需要在每次迭代时扫描邻近矩阵，并且考虑到我们采取 n 步，我们得到的复杂度为 O(n3)。 它的计算成本很高，尤其是在大数据集上。

有可能将其降低到 O(n2logn)，但是与其他聚类算法（如 K-means）相比，它仍然过于昂贵。 如果您想了解更多关于分析算法的空间和时间复杂度以及优化成本函数的信息，您可以前往 upGrad 的数据科学和机器学习课程。

限制

• 我们已经讨论了第一个限制：空间和时间复杂度。 很明显，层次聚类在大数据集的情况下是不利的。 即使用更快的计算机管理时间复杂度，空间复杂度也太高了。 尤其是当我们将它加载到 RAM 中时。 而且，当我们在Python中实现层次聚类时，速度问题会更加严重。 Python 很慢，如果涉及到大任务，它肯定会吃亏。
• 其次，没有优化的接近技术。 如果我们看到每个都有多个问题和限制，这会使算法的内部机制未优化。
• 当我们查看聚类决策时，它们是不可伸缩的。 含义-一旦将聚类应用于确定的迭代，它将不会在进一步的迭代中改变，直到终止。 因此，如果由于结构上的不准确，算法在任何时候选择了错误的集群来合并或拆分，它是不可撤销的。
• 如果我们仔细观察算法，我们没有明确的目标函数被最小化。 在其他算法中，我们尝试优化一个明确的函数。 例如，在 K-means 中，我们有一个明确的成本函数，我们将其最小化，而层次聚类不是这种情况。

查看：每个数据科学家都应该知道的 9 大数据科学算法

结论

尽管在处理大型数据集时存在一定的局限性，但这种类型的聚类算法在处理中小型数据集时很有吸引力。 由于对时间和空间复杂度的惊人需求， Python 中的层次聚类算法在架构或模式方面没有太多发展。

而且，现在确实是大数据的时代。 这意味着我们确实需要可扩展性更好的算法。 但是，如果我们不确定集群的数量，或者我们需要有效地改进分析， Python 中的层次聚类可能是一个令人满意的选择。

有了这个，您现在知道如何在 Python 中实现层次聚类。

要了解更多此类算法和方法在机器学习和数据科学中的应用，请查看 upGrad 提供的课程。 我们为您想要遵循的任何职业道路提供累积计划。

这些课程由顶级专业人士以及 IIIT-B 的教授策划。 有关更多信息，请前往upGrad 。 如果您对学习数据科学以走在快节奏的技术进步的前沿感到好奇，请查看 upGrad 和 IIIT-B 的数据科学执行 PG 计划。