Clustering Jerárquico en Python [Conceptos y Análisis]

Con el aumento del flujo de datos sin procesar y la necesidad de análisis, el concepto de aprendizaje no supervisado se hizo popular con el tiempo. Se utiliza para obtener información de conjuntos de datos que consisten en datos de entrada sin valores objetivo etiquetados. Antes de comenzar a discutir la agrupación jerárquica en Python y aplicar el algoritmo en varios conjuntos de datos, revisemos la idea básica de la agrupación.

El agrupamiento se ocupa principalmente de la clasificación de datos sin procesar. Comprende la agrupación de diferentes puntos de datos, que son los más similares entre sí. Estos grupos se denominan clusters, los cuales se forman en base a la métrica de similitud o clustering definida.

Introducción

El agrupamiento jerárquico se ocupa de los datos en forma de árbol o de una jerarquía bien definida. El proceso implica tratar con dos grupos a la vez. El algoritmo se basa en una matriz de similitud o distancia para las decisiones computacionales. Es decir, qué dos grupos fusionar o cómo dividir un grupo en dos. Con estas dos opciones en mente, tenemos dos tipos de agrupamiento jerárquico . Si es un principiante y está interesado en obtener más información sobre la ciencia de datos, consulte nuestros cursos de ciencia de datos de las mejores universidades.

Uno de los aspectos críticos del algoritmo es la matriz de similitud (también conocida como matriz de proximidad), ya que todo el algoritmo procede en base a ella. Hay muchos métodos de proximidad que se analizan más adelante en el artículo.

Tipos

El agrupamiento jerárquico tiene dos tipos:

1. Agrupación aglomerativa
2. Agrupación divisiva

Los tipos son por la funcionalidad fundamental: la forma de desarrollar la jerarquía. Aglomerative es un generador de jerarquía de abajo hacia arriba, mientras que divisive es un generador de jerarquía de arriba hacia abajo.

Aglomerative toma todos los puntos como grupos individuales y luego los fusiona en cada iteración, dos a la vez. Divisive comienza asumiendo todos los datos como un grupo y los divide hasta que todos los puntos se convierten en grupos individuales.

El resultado es un conjunto de clústeres anidados que pueden percibirse como un árbol jerárquico. La mejor manera de verlo es convertir la estructura del conjunto en un dendrograma para ver la jerarquía.

A continuación, se muestra un ejemplo simple de un dendrograma frente a la representación del conglomerado:

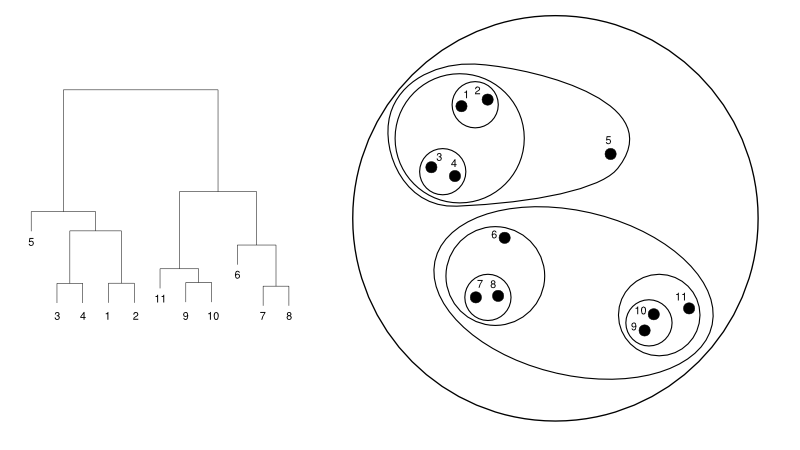
Fuente

Aquí, el agrupamiento puede funcionar de cualquier manera, pero el resultado será una colección de clústeres. Los puntos de datos 1, 2, 3, 4, 5 y 6 se agrupan en dos a la vez. Y la formación de la jerarquía se puede ver en la figura de la izquierda, que trata del dendrograma de la misma. El mismo análisis ayudaría a comprender la decisión de los conglomerados.

Decidir el número de clústeres

Una de las características más útiles de este algoritmo es que puede extraer tantos clústeres como desee una vez que finaliza el algoritmo. Es bastante diferente del algoritmo K-means. En K-means, necesitamos pasar el hiperparámetro no-of-clusters. Significa que una vez que el algoritmo complete el cálculo, tendríamos esa cantidad de grupos. Pero, si necesitamos más clústeres más adelante, no podemos ajustarlos tan fácilmente. La única opción sería cambiar el parámetro y volver a entrenar el modelo.

Mientras que, cuando se trata de la agrupación jerárquica, puede establecer la cantidad de clústeres más adelante. Puedes tomar dos racimos al final. Si no está satisfecho, puede tomar los cinco grupos formados en el paso penúltimo o de nivel superior. Depende de ti. Por lo tanto, una vez entrenado, no necesita volver a entrenar el modelo para obtener más o menos clústeres. Se puede lograr simplemente cortando el dendrograma al nivel que desee.

Como tenemos los conceptos abajo, analicemos el funcionamiento de la agrupación jerárquica en Python .

Para el experimento, vamos a utilizar la biblioteca de aprendizaje sci-kit para los algoritmos de agrupación. También usaríamos el módulo cluster.dendrogram de SciPy para visualizar y comprender el proceso de "corte" para limitar la cantidad de grupos.

importar numpy como np

X = np.matriz([[3,5],

[12,9],

[13,17],

[14,14],

[60,52],

[55,63],

[69,59],])

Se vería algo como esto en una trama:

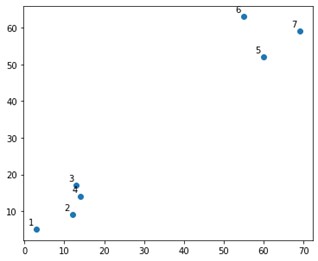
Bueno, vemos que tenemos dos grupos definitivos, en las esquinas superior e inferior. Veamos si el algoritmo puede resolverlo o no.

Estaríamos usando la función AgglomerativeClustering del módulo sklearn.clustering.

de sklearn.cluster importar AgglomerativeClustering

cluster = AgglomerativeClustering(n_clusters=2, affinity='euclidean', linkage='ward')

clúster.fit_predict(X)

Aquí, especificamos los clústeres, que no es un hiperparámetro. Sin embargo, solo lo pasamos para aclarar las clases de predicción. Usaríamos la función fit_predict para entrenar y predecir las clases sobre X.

Es importante tener en cuenta que el agrupamiento aglomerativo se usa más que el divisivo, ya que es más simple de ejecutar. La idea de fusionar grupos basados ​​en matrices de proximidad parece más fácil que dividir un grupo en dos a través de algún mecanismo.

Leer: Scikit-learn en Python: características, requisitos previos, pros y contras

Para comprender claramente lo que sucedió arriba, observe los pasos involucrados en el algoritmo:

Funcionamiento del algoritmo

Estos son los pasos para ejecutar el agrupamiento aglomerativo:

1. Defina cada punto de datos como un grupo
2. Calcular la métrica de proximidad inicial
3. Combinar dos clústeres que sean los "más cercanos" o similares según la métrica
4. Revise la métrica de proximidad y repita el tercer paso hasta que quede un solo grupo.

Entonces, aquí lo único que queda por entender es el impacto de los diferentes métodos de proximidad. Como sabes, principalmente, existen cuatro tipos de métodos de proximidad en el agrupamiento jerárquico. Esto también se conoce como similitud entre grupos.

Los métodos (o vinculación, como se define en el código) incluyen:

1. MIN o enlace único
2. Enlace MAX o completo
3. Vinculación promedio
4. Enlace centroide
5. Funciones exclusivas de las funciones objetivo

Los resultados de la misma se pueden visualizar fácilmente aplicando la opción de enlace mientras se crean los dendrogramas.

Para visualizar la salida del modelo, solo necesitamos un pequeño fragmento de código de la siguiente manera:

plt.dispersión(X[:,0],X[:,1], c=cluster.labels_, cmap='invierno')

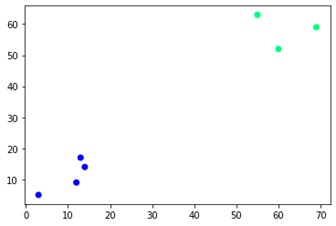
Como puede ver, hay dos grupos diferentes en las esquinas opuestas. También puede jugar con números de grupos y ver resultados diferentes. Todo se puede controlar cortando dendrogramas. Para entender eso, escribamos un pequeño fragmento para la visualización de la creación de dendrogramas.

Vamos a utilizar funciones de dendrograma y enlace del módulo scipy.cluster.hierarchy. Aquí, definimos el enlace que queremos usar. Necesitamos pasar ese objeto a la función dendrograma para generar la jerarquía.

de scipy.cluster.hierarchy dendrograma de importación, vinculación

vinculado = vinculación (X, 'completo')

etiquetaLista = rango (1, 8)

plt.figura(tamañofig=(10, 7))

dendrograma (vinculado,

orientación='superior',

etiquetas=listadeetiquetas,

distancia_ordenar='descendente',

show_leaf_counts=Verdadero)

plt.mostrar()

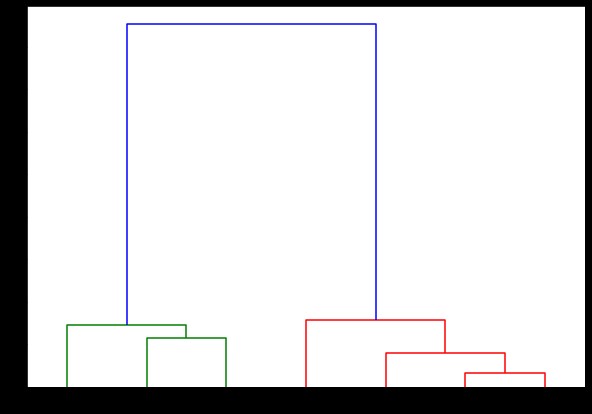
Aquí puede visualizar cómo se forman los grupos en cada iteración. Entonces, puede cortar el dendrograma en cualquier nivel que desee, y terminaría con esa cantidad de grupos. Por lo tanto, debido a la creación de esta jerarquía, puede variar la cantidad de clústeres después de una sola ejecución del algoritmo y los datos. Es lo que le da al agrupamiento jerárquico una ventaja sobre otros algoritmos como K-means.

Ahora, veamos cómo usar el agrupamiento jerárquico en Python en un conjunto de datos de uso común: IRIS . Estaríamos leyendo el conjunto de datos de un csv local. y solo eche un vistazo a cómo se ve el conjunto de datos y qué necesitamos clasificar.

importar numpy como np

importar pandas como pd

importar matplotlib.pyplot como plt

% matplotlib en línea

datos = pd.read_csv('iris.csv')

datos.head()

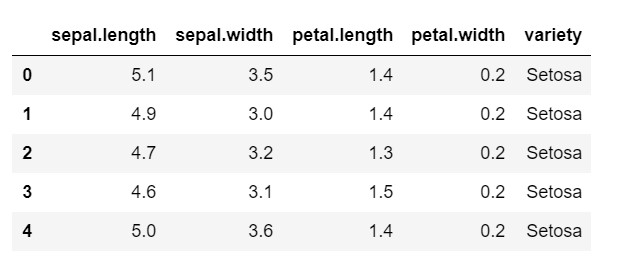
Como puede ver, la variable objetivo es la clase 'variedad'. Esto está en formato de cadena que debe convertirse en números, ya que el modelo requiere etiquetas codificadas. Para hacer esto, estaríamos usando el codificador de etiquetas de la biblioteca de preprocesamiento de sklearn. Un simple ajuste y transformación para convertirlos en números.

del preprocesamiento de importación de sklearn

le = preprocesamiento.LabelEncoder()

le.fit(datos['variedad'])

datos['variedad'] = le.transform(datos['variedad'])

Ahora, si creamos un dendrograma sobre esto, encontramos varias iteraciones y mapas. Así es como se ve con un solo enlace. Si usamos el mismo código y lo ejecutamos con enlace centroide o completo, los dendogramas diferirían un poco. La lógica sigue siendo la misma, pero los diferentes vínculos definitivamente afectarían el orden de la fusión de los clústeres.

de scipy.cluster.hierarchy dendrograma de importación, vinculación

vinculado = vinculación (datos, 'sala')

plt.figura(tamañofig=(10, 7))

dendrograma (vinculado)

plt.mostrar()

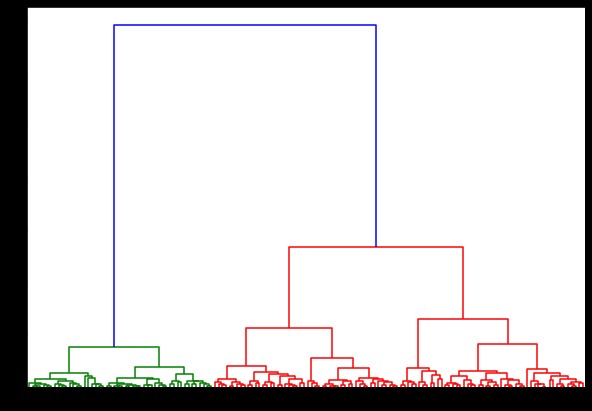
Ahora, al aplicar la agrupación en clústeres en el conjunto de datos, usaríamos dos enlaces diferentes y vería claramente qué diferencia tiene realmente al definir los clústeres. Como ya hemos visto en el codificador de etiquetas, tenemos 3 clases diferentes, por lo que podemos aplicar 3 grupos al principio.

de sklearn.cluster importar AgglomerativeClustering

cluster = AgglomerativeClustering(n_clusters=3, affinity='euclidean', linkage='complete')

cluster.fit_predict(datos)

plt.figura(tamañofig=(10, 7))

plt.dispersión(datos['sépalo.longitud'], datos['pétalo.longitud'], c=cluster.etiquetas_)

Como puede ver en la figura anterior, en la clasificación de 3 grupos, los vínculos muestran cambios visibles en la predicción. Mire la vinculación de la sala primero. Predice correctamente las etiquetas al mantener definido el grupo anterior, aunque hay una pequeña mezcla de valores en los dos grupos. Pero, cuando vemos el enlace completo, rompe el grupo y clasifica incorrectamente algunos de los valores.

Como sabemos en los métodos de proximidad, el enlace completo tiende a romper los grupos más grandes, como podemos ver arriba. El método de la sala o el método de vínculo único es menos vulnerable a estos problemas. Esto fue para los conjuntos de datos simples. Veamos cómo el algoritmo sufre y se ve afectado por algunos conjuntos de datos ruidosos.

Uno de esos conjuntos de datos es el conjunto de datos de predicción Pulsar o el conjunto de datos HTRU2 . El conjunto de datos es más grande, ya que contiene alrededor de 18.000 muestras. Si se ve con una perspectiva de ML, el conjunto de datos tiene un tamaño bastante regular, o incluso menor. Pero, comparativamente, es más pesado que el conjunto de datos de IRIS. La necesidad de implementación en un conjunto de datos variado es analizar el rendimiento de la agrupación jerárquica en Python . Para comprender claramente las formas y ventajas de las implementaciones,

pulsar_data = pd.read_csv('pulsar_stars.csv')

pulsar_data.head()

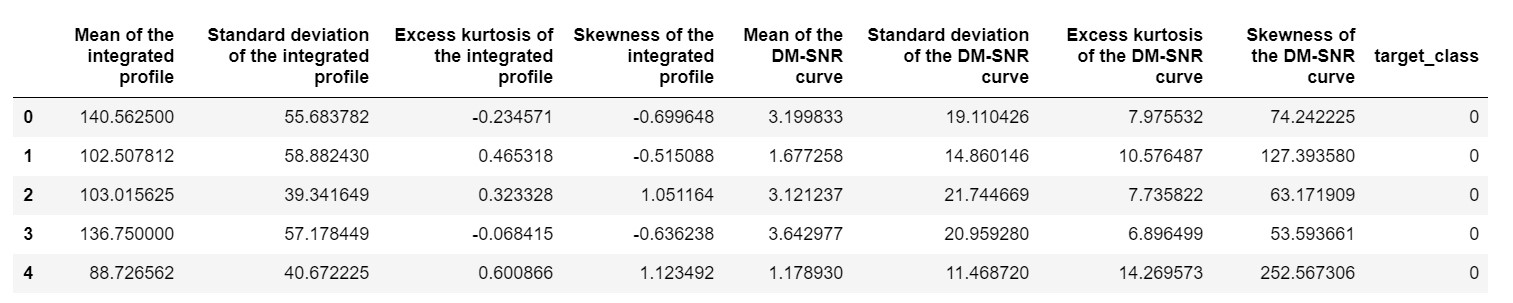
necesitaríamos normalizar el conjunto de datos para que no se sesgue debido a valores extremos.

desde sklearn.preprocessing importar normalizar

pulsar_data = normalizar(pulsar_data)

Estaríamos usando el código estándar, pero esta vez estamos cronometrando ambos cálculos.

%%hora

de scipy.cluster.hierarchy dendrograma de importación, vinculación

vinculado = vinculación (pulsar_data, 'sala')

plt.figura(tamañofig=(10, 7))

dendrograma (vinculado)

plt.mostrar()

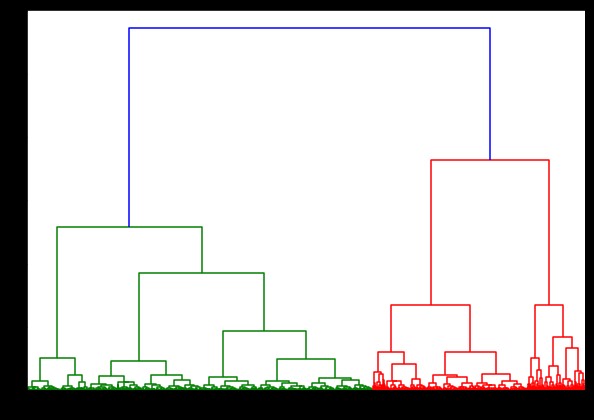
El tiempo para generar un dendrograma en el conjunto de datos de IRIS fue de 6 segundos. El tiempo para generar un dendrograma en el conjunto de datos HTRU2 fue de 13 minutos y 54 segundos. Pero esto no es nada en comparación con el cambio en las predicciones debido a los diferentes vínculos que observa en el modelo entrenado con el conjunto de datos HTRU2.

Sigamos el mismo procedimiento que hicimos antes. Esta vez haríamos predicciones sobre cada enlace.

La siguiente figura muestra las predicciones de agrupamiento con cada enlace:

cluster = AgglomerativeClustering(n_clusters=2, affinity='euclidean', linkage='average') #así como completo, barrio y único

cluster.fit_predict(pulsar_data)

plt.figura(tamañofig=(10, 7))

plt.dispersión(pulsar_data[:,1], pulsar_data[:,7], c=cluster.labels_)

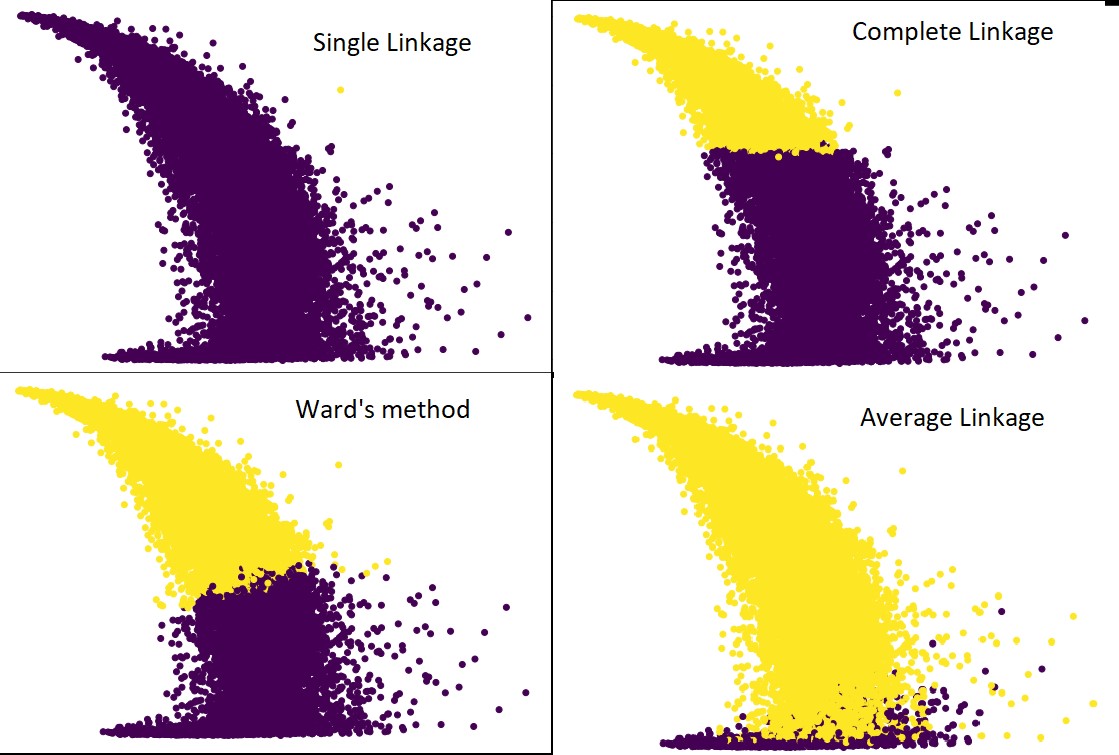
Sí, de hecho es sorprendente cuánto difieren las predicciones entre sí. Esto muestra la importancia de la matriz de proximidad en la agrupación jerárquica.

Como puede ver, el enlace único abarca casi todos los puntos, ya que la distancia mínima entre dos clústeres define la métrica de proximidad. Esto lo hace vulnerable a los datos ruidosos. Si vemos el enlace completo, definitivamente divide los datos en dos grupos, pero es posible que haya roto el grupo grande solo por su proximidad.

El vínculo promedio es una compensación entre los dos. Se ve menos afectado por el ruido, pero aún puede romper grandes grupos, pero con menor probabilidad. Y maneja mejor la clasificación.

A veces se utilizan funciones objetivas como el método de Ward para inicializar otros métodos de agrupación como K-means. Este método, al igual que el enlace promedio, tiene una compensación entre los métodos de enlace simple y completo. Las funciones objetivas como el método de la sala se utilizan principalmente en soluciones personalizadas para disminuir la probabilidad de clasificación errónea. Y lo vemos funcionando bien.

Aprender: Análisis de conglomerados en minería de datos: aplicaciones, métodos y requisitos

Complejidad de tiempo y espacio

Solo para dar una idea, considere la forma en que se define y calcula la métrica de proximidad. La métrica de proximidad requiere almacenar la distancia entre cada par de clústeres dentro del mapa de datos. Da lugar a la complejidad del espacio: O(n2). Es un gran número. Para ponerlo en perspectiva, imagina que tenemos 1.000.000 de puntos. Eso llevará los requisitos de espacio a 1012 puntos. Tomando un promedio aproximado y pesado al aproximar el tamaño de un punto como un byte, obtenemos el tamaño de datos en 1 TB. Y esto debe almacenarse en la memoria RAM, no en el disco duro.

En segundo lugar, viene la complejidad del tiempo. Por la necesidad de escanear la matriz de proximidad en cada iteración y considerando que tomamos n pasos, obtenemos la complejidad como O(n3). Es computacionalmente costoso, especialmente en grandes conjuntos de datos.

Es posible reducirlo a O(n2logn), pero sigue siendo demasiado costoso en comparación con otros algoritmos de agrupación, como K-means. Si desea obtener más información sobre el análisis de la complejidad espacial y temporal de los algoritmos y la optimización de las funciones de costo, puede dirigirse a los Programas de upGrad en ciencia de datos y aprendizaje automático.

Limitaciones

• Ya hemos discutido la primera limitación: Complejidad de espacio y tiempo. Es obvio que la agrupación jerárquica no es favorable en el caso de grandes conjuntos de datos. Incluso si la complejidad del tiempo se gestiona con máquinas computacionales más rápidas, la complejidad del espacio es demasiado alta. Sobre todo cuando lo cargamos en la memoria RAM. Y, el problema de la velocidad aumenta aún más cuando estamos implementando el agrupamiento jerárquico en Python. Python es lento, y si se trata de grandes tareas, definitivamente sufrirá.
• En segundo lugar, no existe una técnica optimizada con proximidad. Si vemos que cada uno tiene múltiples problemas y limitaciones, esto hace que el mecanismo interno del algoritmo no esté optimizado.
• Cuando observamos las decisiones de agrupación, no son retractables. Significado: una vez que se ha aplicado la agrupación en clústeres para una iteración definida, no se cambiará en más iteraciones hasta la terminación. Por lo tanto, si debido a imprecisiones estructurales, el algoritmo, en cualquier momento, elige grupos incorrectos para combinar o dividir, es irrevocable.
• Si miramos de cerca el algoritmo, no tenemos una función objetivo clara que se esté minimizando. En otros algoritmos, hay una función definida que tratamos de optimizar. Por ejemplo, en K-means tenemos una función de costo clara que minimizamos, lo que no es el caso con el agrupamiento jerárquico.

Consulte: Los 9 algoritmos principales de ciencia de datos que todo científico de datos debe conocer

Conclusión

Aunque existen ciertas limitaciones cuando se trata de grandes conjuntos de datos, este tipo de algoritmo de agrupación es atractivo cuando se trata de conjuntos de datos de pequeña a mediana escala. El algoritmo de agrupamiento jerárquico en Python no ha visto mucho desarrollo en arquitectura o esquema debido a su alarmante necesidad de complejidad de tiempo y espacio.

Y, es cierto que ahora mismo, es el momento del Big Data. Significa que requerimos algoritmos que escalan mejor. Pero, aun así, en los casos en que no estamos seguros del número de clústeres, o necesitamos refinar el análisis de manera eficiente, el agrupamiento jerárquico en Python puede ser una opción satisfactoria.

Con esto, ahora sabe cómo implementar el agrupamiento jerárquico en Python.

Para comprender más algoritmos de este tipo y aplicaciones de métodos en aprendizaje automático y ciencia de datos, eche un vistazo a las ofertas de cursos de upGrad. Disponemos de programas acumulativos para cualquiera de las carreras que quieras seguir.

Los programas están curados por los mejores profesionales, así como por los profesores de IIIT-B. Para obtener más información, diríjase a upGrad . Si tiene curiosidad por aprender ciencia de datos para estar al frente de los avances tecnológicos vertiginosos, consulte el Programa ejecutivo PG en ciencia de datos de upGrad & IIIT-B.