Clustering Hierárquico em Python [Conceitos e Análise]

Com o aumento do fluxo de dados brutos e a necessidade de análise, o conceito de aprendizado não supervisionado se popularizou ao longo do tempo. Ele é usado para extrair insights de conjuntos de dados que consistem em dados de entrada sem valores de destino rotulados. Antes de começarmos a discutir o agrupamento hierárquico em Python e aplicar o algoritmo em vários conjuntos de dados, vamos revisitar a ideia básica do agrupamento.

Clustering lida principalmente com a classificação de dados brutos. Consiste em agrupar diferentes pontos de dados, que são mais semelhantes entre si. Esses grupos são chamados de clusters, que são formados com base na métrica de similaridade ou clustering definida.

Introdução

O agrupamento hierárquico lida com dados na forma de uma árvore ou uma hierarquia bem definida. O processo envolve lidar com dois clusters por vez. O algoritmo conta com uma matriz de similaridade ou distância para decisões computacionais. Ou seja, quais dois clusters devem ser mesclados ou como dividir um cluster em dois. Com essas duas opções em mente, temos dois tipos de agrupamento hierárquico . Se você é iniciante e está interessado em aprender mais sobre ciência de dados, confira nossos cursos de ciência de dados das melhores universidades.

Um dos aspectos críticos do algoritmo é a matriz de similaridade (também conhecida como matriz de proximidade), pois todo o algoritmo procede com base nela. Existem muitos métodos de proximidade que são discutidos mais adiante no artigo.

Tipos

O clustering hierárquico tem dois tipos:

1. Agrupamento aglomerativo
2. Agrupamento divisivo

Os tipos são de acordo com a funcionalidade fundamental: a maneira de desenvolver hierarquia. Aglomerativo é um gerador de hierarquia de baixo para cima, enquanto o divisivo é um gerador de hierarquia de cima para baixo.

Aglomerativa pega todos os pontos como clusters individuais e os mescla em cada iteração, dois de cada vez. A divisão começa assumindo todos os dados como um cluster e os divide até que todos os pontos se tornem clusters individuais.

O resultado é um conjunto de clusters aninhados que podem ser percebidos como uma árvore hierárquica. A melhor maneira de visualizá-lo é converter a estrutura do conjunto em um dendrograma para visualizar a hierarquia.

Veja a seguir um exemplo simples de um dendrograma versus a representação do cluster:

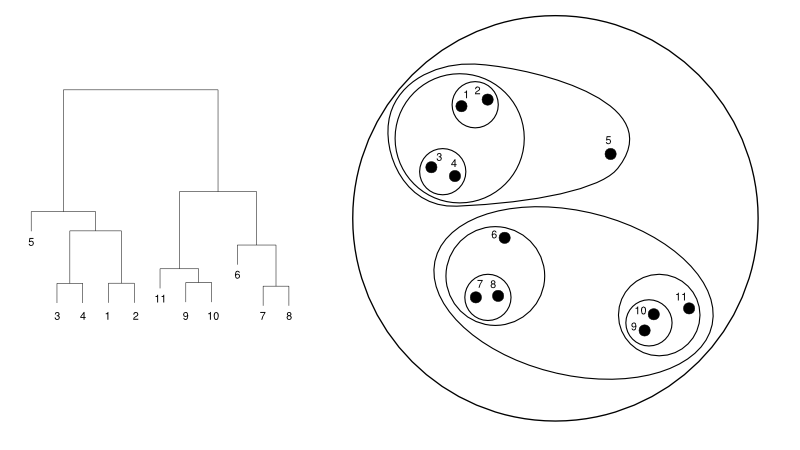
Fonte

Aqui, o agrupamento pode funcionar de qualquer maneira, mas o resultado será uma coleção de agrupamentos. Os pontos de dados 1, 2, 3, 4, 5 e 6 são agrupados em dois por vez. E a formação da hierarquia pode ser vista na figura da esquerda, que trata do dendrograma da mesma. A mesma análise ajudaria no entendimento da decisão dos clusters.

Decidindo o número de clusters

Um dos recursos mais úteis desse algoritmo é que você pode extrair quantos clusters quiser quando o algoritmo terminar. É bem diferente do algoritmo K-means. Em K-means, precisamos passar o hiperparâmetro no-of-clusters. Isso significa que, uma vez que o algoritmo conclua a computação, teríamos esse número de clusters. Mas, se precisarmos de mais clusters posteriormente, não podemos ajustar com tanta facilidade. A única opção seria alterar o parâmetro e treinar o modelo novamente.

Considerando que, quando se trata do cluster hierárquico, você pode definir o número de clusters posteriormente. Você pode pegar dois clusters no final. Se não estiver satisfeito, você pode pegar os cinco grupos formados na penúltima etapa ou na etapa de nível superior. Depende de você. Portanto, uma vez treinado, você não precisa treinar novamente o modelo para obter mais ou menos clusters. Isso pode ser feito simplesmente cortando o dendrograma no nível desejado.

Como temos os conceitos abaixo, vamos discutir o funcionamento do agrupamento hierárquico em Python .

Para o experimento, usaremos a biblioteca sci-kit learn para os algoritmos de clustering. Também usaríamos o módulo cluster.dendrogram do SciPy para visualizar e entender o processo de “corte” para limitar o número de clusters.

importar numpy como np

X = np.array([[3,5],

[12,9],

[13,17],

[14,14],

[60,52],

[55,63],

[69,59],])

Seria algo assim em um enredo:

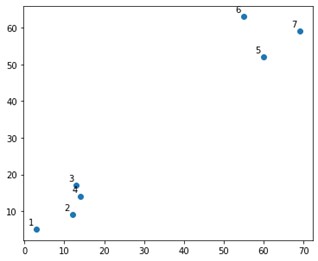
Bem, vemos que temos dois clusters definitivos, nos cantos superior e inferior. Vamos ver se o algoritmo consegue descobrir ou não.

Estaríamos usando a função AgglomerativeClustering do módulo sklearn.clustering.

de sklearn.cluster import AglomerativeClustering

cluster = AgglomerativeClustering(n_clusters=2, afinidade='euclidiano', linkage='ward')

cluster.fit_predict(X)

Aqui, especificamos os clusters, que não são um hiperparâmetro. No entanto, apenas passamos para deixar as classes de previsão claras. Usaríamos a função fit_predict para treinar e prever as classes sobre X.

É importante notar que o agrupamento aglomerativo é mais usado do que o divisivo, pois é mais simples de executar. A ideia de mesclar clusters com base em matrizes de proximidade parece mais fácil do que dividir um cluster em dois por meio de algum mecanismo.

Leia: Scikit-learn in Python: recursos, pré-requisitos, prós e contras

Para entender claramente o que aconteceu acima, observe as etapas envolvidas no algoritmo:

Funcionamento do algoritmo

Aqui estão as etapas para executar o clustering aglomerativo:

1. Defina cada ponto de dados como um cluster
2. Calcular a métrica de proximidade inicial
3. Mesclar dois clusters que são os “mais próximos” ou semelhantes com base na métrica
4. Revise a métrica de proximidade e repita a terceira etapa até que um único cluster permaneça.

Então, aqui a única coisa que resta entender é o impacto de diferentes métodos de proximidade. Como você sabe, principalmente, existem quatro tipos de métodos de proximidade no agrupamento hierárquico. Isso também é conhecido como similaridade entre clusters.

Os métodos (ou ligação, conforme definido no código) incluem:

1. MIN ou ligação única
2. MAX ou ligação completa
3. Ligação média
4. Ligação centroide
5. Funções exclusivas de funções objetivo

Os resultados do mesmo podem ser facilmente visualizados aplicando a opção de vinculação durante a criação dos dendrogramas.

Para visualizar a saída do modelo, precisamos apenas de um pequeno trecho de código da seguinte forma:

plt.scatter(X[:,0],X[:,1], c=cluster.labels_, cmap='inverno')

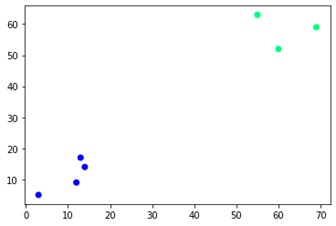
Como você pode ver, existem dois clusters diferentes nos cantos opostos. Você também pode brincar com números de cluster e ver resultados diferentes. A coisa toda pode ser conduzida cortando dendrogramas. Para entender isso, vamos escrever um pequeno trecho para a visualização da criação de dendrogramas.

Vamos usar as funções de dendrograma e de ligação do módulo scipy.cluster.hierarchy. Aqui, definimos a ligação que queremos usar. Precisamos passar esse objeto para a função dendrograma para gerar a hierarquia.

de scipy.cluster.hierarchy import dendrogram, linkage

link = link(X, 'completo')

listaLista = intervalo(1, 8)

plt.figure(figsize=(10, 7))

dendrograma (ligado,

orientação='topo',

rótulos=listaLista,

distance_sort='descendente',

show_leaf_counts=Verdadeiro)

plt.show()

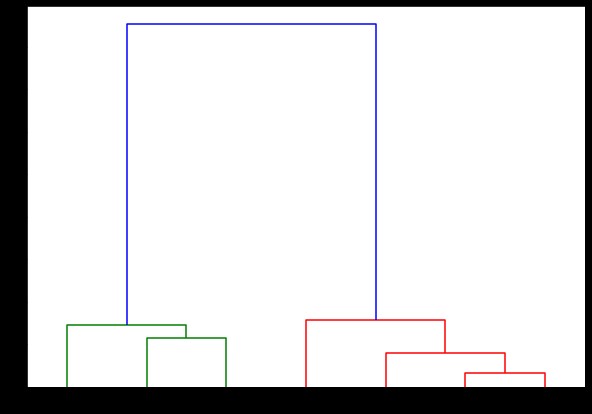
Aqui, você pode visualizar como os clusters são formados em cada iteração. Assim, você pode cortar o dendrograma em qualquer nível que desejar, e acabaria com tantos clusters. Portanto, devido à criação dessa hierarquia, você pode variar o número de clusters após apenas uma execução no algoritmo e nos dados. É o que dá ao agrupamento hierárquico uma vantagem sobre outros algoritmos como K-means.

Agora, vamos ver como usar clustering hierárquico em Python em um conjunto de dados comumente usado: IRIS . Estaríamos lendo o conjunto de dados de um csv local. e dê uma olhada na aparência do conjunto de dados e no que precisamos classificar.

importar numpy como np

importar pandas como pd

importar matplotlib.pyplot como plt

%matplotlib em linha

dados = pd.read_csv('iris.csv')

data.head()

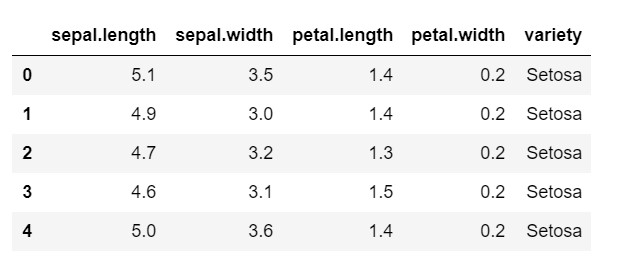
Como você pode ver, a variável de destino é a classe 'variedade'. Isso está em formato de string que precisa ser convertido em números, pois o modelo requer rótulos codificados. Para fazer isso, usaríamos o codificador de rótulos da biblioteca de pré-processamento do sklearn. Um simples ajuste e transformação para convertê-los em números.

do pré-processamento de importação do sklearn

le = pré-processamento.LabelEncoder()

le.fit(data['variedade'])

data['variedade'] = le.transform(data['variedade'])

Agora, se criarmos um dendrograma sobre isso, encontraremos várias iterações e mapas. É assim que fica com uma única ligação. Se usarmos o mesmo código e executá-lo com ligação completa ou centroide, os dendrogramas difeririam um pouco. A lógica permanece a mesma, mas diferentes ligações afetariam definitivamente a ordem da fusão dos clusters.

de scipy.cluster.hierarchy import dendrogram, linkage

link = linkage(dados, 'ward')

plt.figure(figsize=(10, 7))

dendrograma (ligado)

plt.show()

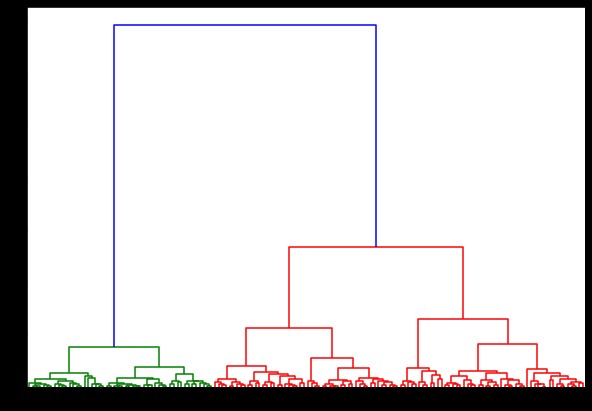
Agora, aplicando o agrupamento no conjunto de dados, usaríamos dois vínculos diferentes e você veria claramente a diferença que ele realmente tem ao definir os agrupamentos. Como já vimos no codificador de rótulos que temos 3 classes diferentes, podemos aplicar 3 clusters no início.

de sklearn.cluster import AglomerativeClustering

cluster = AgglomerativeClustering(n_clusters=3, afinidade='euclidiano', linkage='completo')

cluster.fit_predict(dados)

plt.figure(figsize=(10, 7))

plt.scatter(data['sepal.length'], data['petal.length'], c=cluster.labels_)

Como você pode ver na figura acima, na classificação de 3 clusters, as ligações mostram mudanças visíveis na previsão. Olhe primeiro para a ligação da ala. Ele prevê corretamente os rótulos mantendo o cluster acima definido, mesmo que haja uma pequena mistura de valores nos dois clusters. Mas, quando vemos a ligação completa, ele quebra o cluster e classificou incorretamente alguns dos valores.

Como sabemos nos métodos de proximidade, a ligação completa tende a quebrar os aglomerados maiores, como podemos ver acima. O método da ala ou o método de ligação única é menos vulnerável a esses problemas. Isso foi para os conjuntos de dados simples. Vamos ver como o algoritmo sofre e é afetado por alguns conjuntos de dados ruidosos.

Um desses conjuntos de dados é o conjunto de dados de previsão Pulsar ou o conjunto de dados HTRU2 . O conjunto de dados é maior, pois contém cerca de 18.000 amostras. Se visto com uma perspectiva de ML, o conjunto de dados tem um tamanho bastante regular ou até menor. Mas, comparativamente, é mais pesado que o conjunto de dados IRIS. A necessidade de implementação em um conjunto de dados variado é analisar o desempenho do cluster hierárquico em Python . Para entender claramente as formas e vantagens das implementações,

pulsar_data = pd.read_csv('pulsar_stars.csv')

pulsar_data.head()

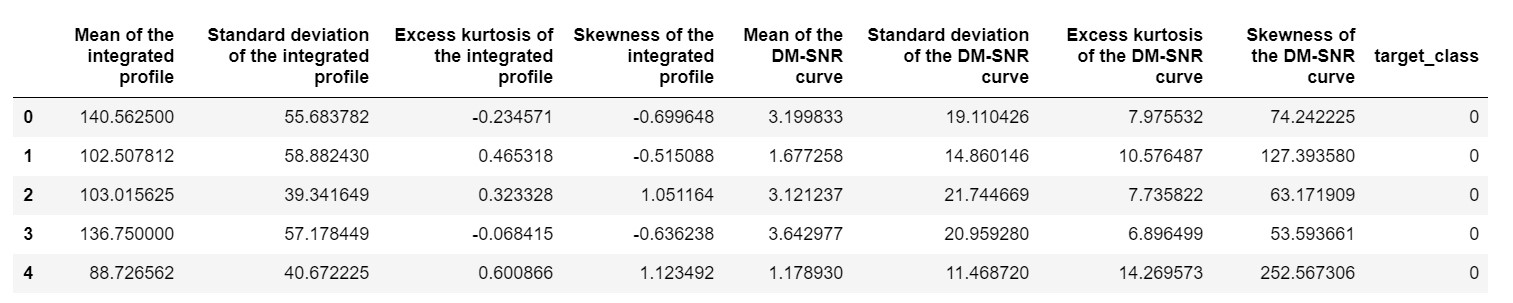
precisaríamos normalizar o conjunto de dados para que ele não viesse devido a valores extremos.

de sklearn.preprocessing importação normalizar

pulsar_data = normalize(pulsar_data)

Estaríamos usando o código padrão, mas desta vez, estamos cronometrando os dois cálculos.

%%Tempo

de scipy.cluster.hierarchy import dendrogram, linkage

link = linkage(pulsar_data, 'ward')

plt.figure(figsize=(10, 7))

dendrograma (ligado)

plt.show()

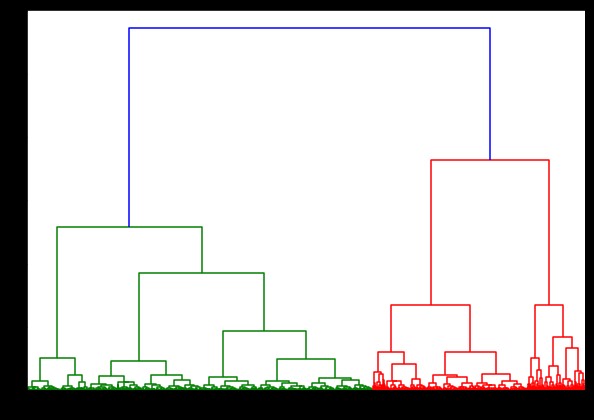
O tempo para gerar um dendrograma no conjunto de dados IRIS foi de 6 segundos. O tempo para gerar um dendrograma no conjunto de dados HTRU2 foi de 13 minutos e 54 segundos. Mas isso não é nada comparado à mudança nas previsões devido a diferentes ligações, que você observa no modelo treinado com o conjunto de dados HTRU2.

Vamos seguir o mesmo procedimento que fizemos antes. Desta vez faríamos previsões em cada ligação.

A figura a seguir mostra as previsões de agrupamento com cada ligação:

cluster = AgglomerativeClustering(n_clusters=2, afinidade='euclidiano', linkage='average') #assim como complete,ward e single

cluster.fit_predict(pulsar_data)

plt.figure(figsize=(10, 7))

plt.scatter(pulsar_data[:,1], pulsar_data[:,7], c=cluster.labels_)

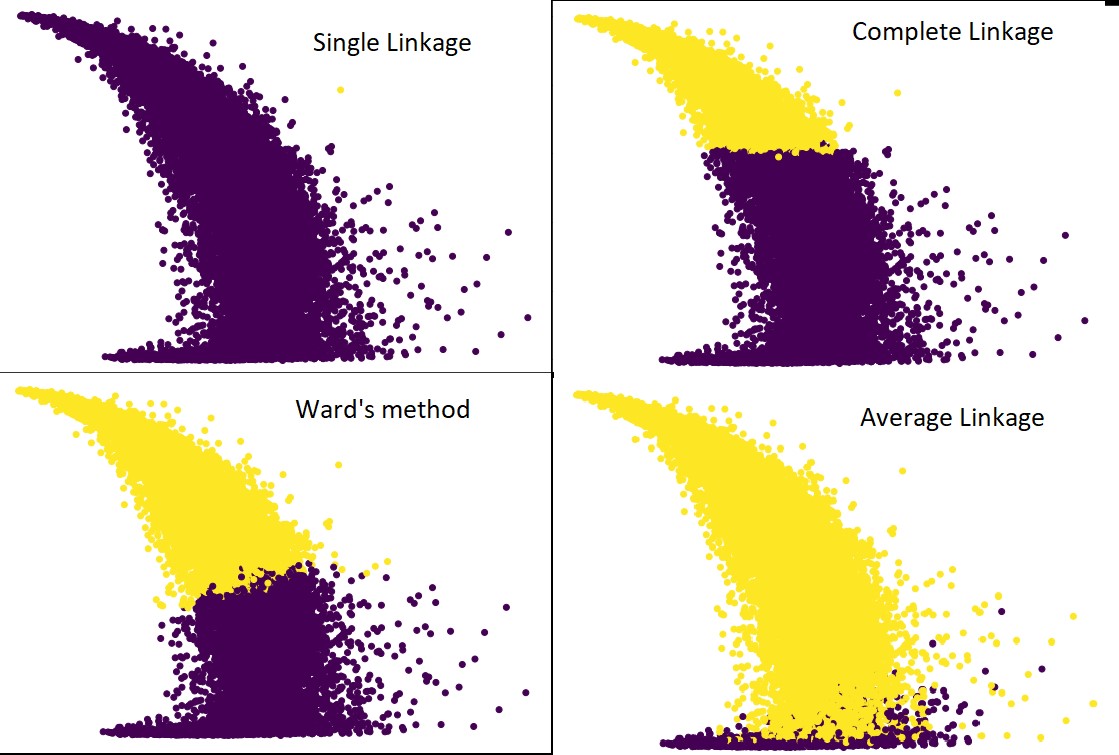
Sim, é realmente surpreendente o quanto as previsões diferem umas das outras. Isso mostra a importância da matriz de proximidade no agrupamento hierárquico.

Como você pode ver, a ligação única abrange quase todos os pontos, pois a distância mínima entre dois clusters define a métrica de proximidade. Isso o torna vulnerável a dados ruidosos. Se virmos a ligação completa, ela definitivamente divide os dados em dois clusters, mas pode ter quebrado o grande cluster apenas devido à sua proximidade.

A ligação média é um trade-off entre os dois. É menos afetado pelo ruído, mas ainda pode quebrar grandes aglomerados, mas com menor probabilidade. E, ele lida melhor com a classificação.

As funções objetivas, como o método do ward, às vezes são usadas para inicializar outros métodos de agrupamento, como o K-means. Este método, assim como o de ligação média, tem um trade-off entre os métodos de ligação simples e completa. Funções objetivas como o método da ala são usadas principalmente em soluções personalizadas para diminuir a probabilidade de erros de classificação. E, nós vemos isso funcionando bem.

Aprenda: Análise de Cluster em Mineração de Dados: Aplicações, Métodos e Requisitos

Complexidade de tempo e espaço

Apenas para entender, considere a forma como a métrica de proximidade é definida e calculada. A métrica de proximidade requer armazenar a distância entre cada par de clusters dentro do mapa de dados. Isso contribui para a complexidade do espaço: O(n2). É um grande número. Para colocar em perspectiva, imagine que temos 1.000.000 de pontos. Isso levará os requisitos de espaço para 1012 pontos. Tomando uma média aproximada e pesada aproximando o tamanho de um ponto como um byte, obtemos o tamanho dos dados em 1 TB. E isso precisa ser armazenado na RAM, não no disco rígido.

Em segundo lugar, vem a complexidade do tempo. Para a necessidade de escanear a matriz de proximidade a cada iteração e considerando que damos n passos, obtemos a complexidade como O(n3). É computacionalmente caro, especialmente em grandes conjuntos de dados.

Pode ser possível reduzi-lo para O(n2logn), mas ainda é muito caro em comparação com outros algoritmos de agrupamento, como K-means. Se você quiser aprender mais sobre como analisar a complexidade de espaço e tempo dos algoritmos e otimizar as funções de custo, você pode ir até os Programas de Ciência de Dados e Aprendizado de Máquina do upGrad.

Limitações

• Já discutimos a primeira limitação: complexidade de espaço e tempo. É óbvio que o agrupamento hierárquico não é favorável no caso de grandes conjuntos de dados. Mesmo que a complexidade do tempo seja gerenciada com máquinas computacionais mais rápidas, a complexidade do espaço é muito alta. Especialmente quando o carregamos na RAM. E, a questão da velocidade aumenta ainda mais quando estamos implementando o cluster hierárquico em Python. O Python é lento e, se houver grandes tarefas, ele definitivamente sofrerá.
• Em segundo lugar, não existe técnica otimizada com proximidade. Se percebermos que cada um tem vários problemas e limitações, isso torna o mecanismo interno do algoritmo não otimizado.
• Quando olhamos para as decisões de agrupamento, elas não são retráteis. Significado - uma vez que o agrupamento tenha sido aplicado para uma iteração definida, ele não será alterado em outras iterações até o término. Assim, se devido a imprecisões estruturais, o algoritmo, em qualquer ponto, escolher clusters errados para combinar ou dividir, é irrevogável.
• Se olharmos atentamente para o algoritmo, não temos uma função objetivo clara que está sendo minimizada. Em outros algoritmos, existe uma função definida que tentamos otimizar. Por exemplo, em K-means temos uma função de custo clara que minimizamos, o que não é o caso do agrupamento hierárquico.

Confira: Os 9 principais algoritmos de ciência de dados que todo cientista de dados deveria conhecer

Conclusão

Embora existam certas limitações quando se trata de grandes conjuntos de dados, esse tipo de algoritmo de agrupamento é atraente ao lidar com conjuntos de dados de pequena e média escala. O algoritmo de agrupamento hierárquico em Python não teve muito desenvolvimento na arquitetura ou esquema devido à sua necessidade alarmante de complexidade de tempo e espaço.

E, é verdade que agora, a hora é de Big Data. Isso significa que exigimos algoritmos que escalam melhor. Mas, ainda assim, nos casos em que não temos certeza do número de clusters, ou precisamos refinar a análise de forma eficiente, o agrupamento hierárquico em Python pode ser uma escolha satisfatória.

Com isso, agora você sabe como implementar clustering hierárquico em Python.

Para entender mais desses algoritmos e aplicações de métodos em Machine Learning e Data Science, dê uma olhada nas ofertas de cursos do upGrad. Temos programas cumulativos para qualquer uma das carreiras que você deseja seguir.

Os programas têm curadoria de profissionais de ponta, bem como dos professores do IIIT-B. Para mais informações, vá até o upGrad . Se você está curioso para aprender ciência de dados para estar na frente dos avanços tecnológicos em ritmo acelerado, confira o Programa PG Executivo em Ciência de Dados do upGrad & IIIT-B.