Pengelompokan Hirarki dengan Python [Konsep dan Analisis]

Dengan meningkatnya aliran data mentah dan kebutuhan akan analisis, konsep pembelajaran tanpa pengawasan menjadi populer dari waktu ke waktu. Ini digunakan untuk menarik wawasan dari kumpulan data yang terdiri dari data input tanpa nilai target berlabel. Sebelum kita mulai membahas pengelompokan hierarkis dengan Python dan menerapkan algoritme pada berbagai kumpulan data, mari kita tinjau kembali ide dasar pengelompokan.

Clustering terutama berkaitan dengan klasifikasi data mentah. Ini terdiri dari pengelompokan titik data yang berbeda bersama-sama, yang paling mirip satu sama lain. Kelompok-kelompok ini disebut cluster, yang dibentuk berdasarkan kesamaan atau clustering metrik yang ditentukan.

pengantar

Pengelompokan hierarki berkaitan dengan data dalam bentuk pohon atau hierarki yang terdefinisi dengan baik. Proses ini melibatkan berurusan dengan dua cluster pada suatu waktu. Algoritma bergantung pada kesamaan atau matriks jarak untuk keputusan komputasi. Artinya, dua cluster mana yang akan digabungkan atau bagaimana membagi cluster menjadi dua. Dengan mempertimbangkan dua opsi ini, kami memiliki dua jenis pengelompokan hierarkis . Jika Anda seorang pemula dan tertarik untuk mempelajari lebih lanjut tentang ilmu data, lihat kursus ilmu data kami dari universitas terkemuka.

Salah satu aspek kritis algoritma adalah matriks kesamaan (juga dikenal sebagai matriks kedekatan), karena keseluruhan algoritma berjalan berdasarkan matriks tersebut. Ada banyak metode kedekatan yang dibahas lebih lanjut dalam artikel ini.

Jenis

Pengelompokan hierarki memiliki dua jenis:

1. Pengelompokan aglomeratif
2. Pengelompokan yang memecah belah

Jenisnya sesuai dengan fungsi mendasar: cara mengembangkan hierarki. Agglomerative adalah generator hierarki bottom-up, sedangkan divisive adalah generator hierarki top-down.

Agglomerative mengambil semua titik sebagai cluster individu dan kemudian menggabungkannya pada setiap iterasi, dua sekaligus. Divisive dimulai dengan mengasumsikan seluruh data sebagai satu cluster dan membaginya hingga semua titik menjadi cluster individu.

Hasilnya adalah sekumpulan cluster bersarang yang dapat dianggap sebagai pohon hierarkis. Cara terbaik untuk melihatnya adalah dengan mengubah struktur himpunan menjadi dendrogram untuk melihat hierarki.

Berikut ini adalah contoh sederhana dari dendrogram versus representasi cluster:

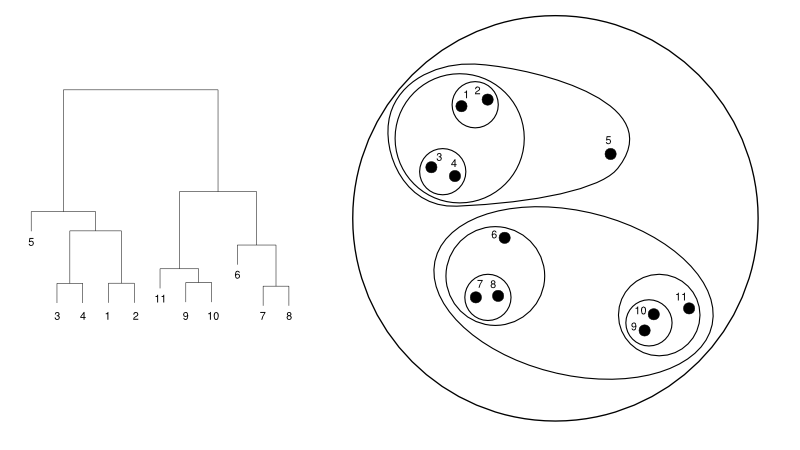
Sumber

Di sini, pengelompokan dapat bekerja dengan cara apa pun, tetapi hasilnya akan menjadi kumpulan klaster. Data titik 1, 2, 3, 4, 5, dan 6 dikelompokkan menjadi dua sekaligus. Dan formasi hierarki dapat dilihat pada gambar kiri, yang berhubungan dengan dendrogram yang sama. Analisis yang sama akan membantu dalam memahami keputusan cluster.

Menentukan jumlah cluster

Salah satu fitur yang paling berguna dari algoritme ini adalah Anda dapat mengekstrak cluster sebanyak yang Anda inginkan setelah algoritme berakhir. Ini sangat berbeda dari algoritma K-means. Dalam K-means, kita perlu melewati hyperparameter no-of-cluster. Artinya, setelah algoritma menyelesaikan perhitungan, kita akan memiliki banyak cluster. Tapi, jika nanti kita membutuhkan lebih banyak cluster, kita tidak bisa menyetelnya dengan mudah. Satu-satunya pilihan adalah mengubah parameter dan melatih model lagi.

Sedangkan untuk hierarki clustering, Anda bisa mengatur jumlah clusternya nanti. Anda dapat mengambil dua cluster di akhir. Jika tidak puas, Anda dapat mengambil lima kelompok yang terbentuk pada langkah kedua dari belakang atau tingkat yang lebih tinggi. Itu tergantung pada Anda. Oleh karena itu, setelah dilatih, Anda tidak perlu melatih ulang model untuk mendapatkan lebih banyak atau lebih sedikit cluster. Hal ini dapat dicapai dengan hanya memotong dendrogram pada tingkat yang Anda inginkan.

Saat kita memiliki konsep, mari kita bahas cara kerja pengelompokan hierarkis dengan Python .

Untuk percobaan, kita akan menggunakan sci-kit learning library untuk algoritma clustering. Kami juga akan menggunakan modul cluster.dendrogram dari SciPy untuk memvisualisasikan dan memahami proses "pemotongan" untuk membatasi jumlah cluster.

impor numpy sebagai np

X = np.array([[3,5],

[12,9],

[13,17],

[14,14],

[60,52],

[55,63],

[69,59],])

Itu akan terlihat seperti ini di plot:

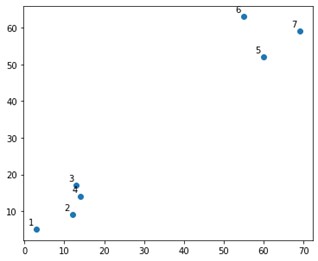
Nah, kami melihat bahwa kami memiliki dua kelompok definitif, di sudut atas dan bawah. Mari kita lihat apakah algoritma dapat mengetahuinya atau tidak.

Kami akan menggunakan fungsi AgglomerativeClustering dari modul sklearn.clustering.

dari sklearn.cluster import AgglomerativeClustering

cluster = AgglomerativeClustering(n_cluster=2, affinity='euclidean', linkage='ward')

cluster.fit_predict(X)

Di sini, kami menentukan cluster, yang bukan hyperparameter. Namun, kami hanya meneruskannya untuk memperjelas kelas prediksi. Kami akan menggunakan fungsi fit_predict untuk melatih serta memprediksi kelas di atas X.

Penting untuk dicatat bahwa pengelompokan aglomeratif lebih banyak digunakan daripada memecah belah karena lebih mudah untuk dieksekusi. Gagasan menggabungkan cluster berdasarkan matriks kedekatan tampaknya lebih mudah daripada membagi cluster menjadi dua melalui beberapa mekanisme.

Baca: Scikit-belajar dengan Python: Fitur, Prasyarat, Pro & Kontra

Untuk memahami dengan jelas apa yang terjadi di atas, lihat langkah-langkah yang terlibat dalam algoritme:

Kerja dari algoritma

Berikut adalah langkah-langkah untuk mengeksekusi agglomerative clustering:

1. Tentukan setiap titik data sebagai sebuah cluster
2. Hitung metrik kedekatan awal
3. Gabungkan dua cluster yang "paling dekat" atau serupa berdasarkan metrik
4. Revisi metrik kedekatan dan ulangi langkah ketiga hingga tersisa satu cluster.

Jadi, di sini satu-satunya hal yang tersisa untuk dipahami adalah dampak dari metode kedekatan yang berbeda. Seperti yang Anda ketahui, terutama, ada empat jenis metode kedekatan dalam pengelompokan hierarkis. Ini juga dikenal sebagai kesamaan antar-cluster.

Metode (atau keterkaitan, seperti yang didefinisikan dalam kode) meliputi:

1. MIN atau Tautan tunggal
2. MAX atau tautan Lengkap
3. Hubungan rata-rata
4. Keterkaitan pusat
5. Fungsi eksklusif dari fungsi tujuan

Hasil yang sama dapat dengan mudah divisualisasikan dengan menerapkan opsi tautan saat membuat dendrogram.

Untuk memvisualisasikan keluaran model, kita hanya membutuhkan potongan kode kecil sebagai berikut:

plt.scatter(X[:,0],X[:,1], c=cluster.labels_, cmap='winter')

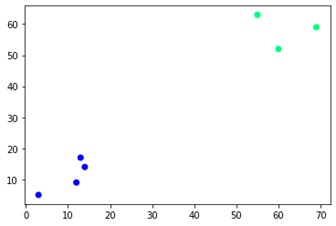
Seperti yang Anda lihat, ada dua kelompok berbeda di sudut yang berlawanan. Anda mungkin juga bermain-main dengan nomor cluster dan melihat hasil yang berbeda. Semuanya dapat digerakkan dengan memotong dendrogram. Untuk memahaminya, mari kita tulis cuplikan kecil untuk visualisasi pembuatan dendrogram.

Kita akan menggunakan fungsi dendrogram dan linkage dari modul scipy.cluster.hierarchy. Di sini, kami mendefinisikan tautan yang ingin kami gunakan. Kita perlu meneruskan objek itu ke fungsi dendrogram untuk menghasilkan hierarki.

dari scipy.cluster.hierarchy import dendrogram, linkage

tertaut = tautan(X, 'selesai')

labelList = rentang(1, 8)

plt.figure(figsize=(10, 7))

dendrogram (tertaut,

orientasi = 'atas',

label=daftarlabel,

distance_sort='menurun',

show_leaf_counts=Benar)

plt.tampilkan()

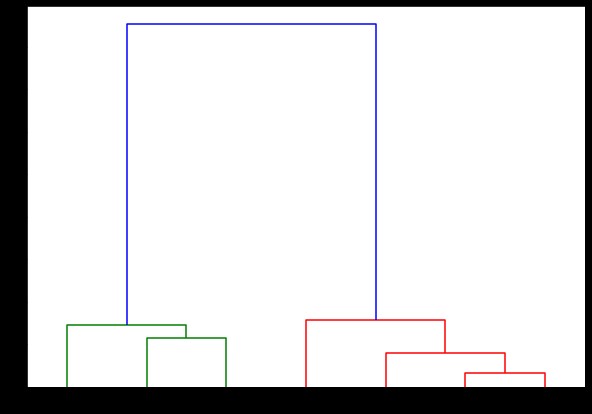
Di sini, Anda dapat memvisualisasikan bagaimana cluster terbentuk pada setiap iterasi. Jadi, Anda dapat memotong dendrogram pada level mana pun yang Anda inginkan, dan Anda akan mendapatkan banyak cluster. Oleh karena itu, karena pembuatan hierarki ini, Anda dapat memvariasikan jumlah cluster setelah hanya satu kali dijalankan melalui algoritme dan data. Inilah yang memberi pengelompokan hierarkis keunggulan pada algoritma lain seperti K-means.

Sekarang, mari kita lihat cara menggunakan pengelompokan hierarkis dengan Python pada kumpulan data yang umum digunakan: IRIS . Kami akan membaca dataset dari csv lokal. dan lihat sekilas bagaimana tampilan dataset dan apa yang perlu kita klasifikasikan.

impor numpy sebagai np

impor panda sebagai pd

impor matplotlib.pyplot sebagai plt

%matplotlib sebaris

data = pd.read_csv('iris.csv')

data.head()

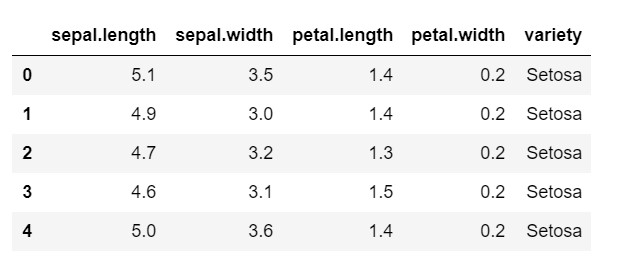
Seperti yang Anda lihat, variabel target adalah kelas 'variasi'. Ini dalam format string yang perlu diubah menjadi angka, karena model memerlukan label yang disandikan. Untuk melakukan ini, kita akan menggunakan encoder label dari library preprocessing sklearn. Kesesuaian sederhana dan transformasi untuk mengubahnya menjadi angka.

dari preprocessing impor sklearn

le = prapemrosesan.LabelEncoder()

le.fit(data['variasi'])

data['variasi'] = le.transform(data['variasi'])

Sekarang, jika kita membuat dendrogram ini, kita menemukan berbagai iterasi dan peta. Ini adalah tampilannya dengan satu tautan. Jika kita menggunakan kode yang sama dan menjalankannya dengan linkage lengkap atau centroid, dendrogram akan sedikit berbeda. Logikanya tetap sama, tetapi keterkaitan yang berbeda pasti akan mempengaruhi urutan penggabungan klaster.

dari scipy.cluster.hierarchy import dendrogram, linkage

tertaut = keterkaitan(data, 'bangsal')

plt.figure(figsize=(10, 7))

dendrogram (tertaut)

plt.tampilkan()

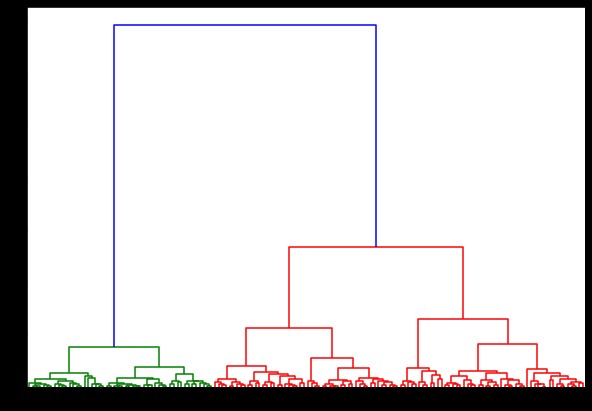
Sekarang, dengan menerapkan pengelompokan pada kumpulan data, kami akan menggunakan dua hubungan yang berbeda, dan Anda akan melihat dengan jelas perbedaan apa yang sebenarnya dimilikinya saat mendefinisikan klaster. Seperti yang telah kita lihat dari encoder label bahwa kita memiliki 3 kelas yang berbeda, jadi kita mungkin menerapkan 3 cluster pada awalnya.

dari sklearn.cluster import AgglomerativeClustering

cluster = AgglomerativeClustering(n_cluster=3, affinity='euclidean', linkage='lengkap')

cluster.fit_predict(data)

plt.figure(figsize=(10, 7))

plt.scatter(data['sepal.length'], data['petal.length'], c=cluster.labels_)

Seperti yang Anda lihat dari gambar di atas, dalam klasifikasi 3-klaster, keterkaitan menunjukkan perubahan prediksi yang terlihat. Lihat dulu ward linkagenya. Ini memprediksi label dengan benar dengan menjaga klaster di atas tetap didefinisikan, meskipun ada sedikit campuran nilai dalam dua klaster. Tapi, ketika kita melihat keterkaitan yang lengkap, itu memecah cluster dan salah mengklasifikasikan beberapa nilai.

Seperti yang kita ketahui dalam metode kedekatan, tautan lengkap memang cenderung memecah kelompok yang lebih besar, seperti yang dapat kita lihat di atas. Metode ward atau metode linkage tunggal kurang rentan terhadap masalah ini. Ini untuk dataset sederhana. Mari kita lihat bagaimana algoritme menderita dan dipengaruhi oleh beberapa kumpulan data yang berisik.

Salah satu kumpulan data tersebut adalah kumpulan data prediksi Pulsar atau kumpulan data HTRU2 . Dataset lebih besar, karena berisi sekitar 18.000 sampel. Jika dilihat dengan perspektif ML, ukuran dataset ini cukup biasa, atau bahkan lebih rendah. Tapi, secara komparatif, ini lebih berat daripada dataset IRIS. Kebutuhan implementasi pada dataset yang bervariasi adalah dengan menganalisis kinerja dari hirarki clustering di Python . Untuk memahami dengan jelas cara dan manfaat implementasi,

pulsar_data = pd.read_csv('pulsar_stars.csv')

pulsar_data.head()

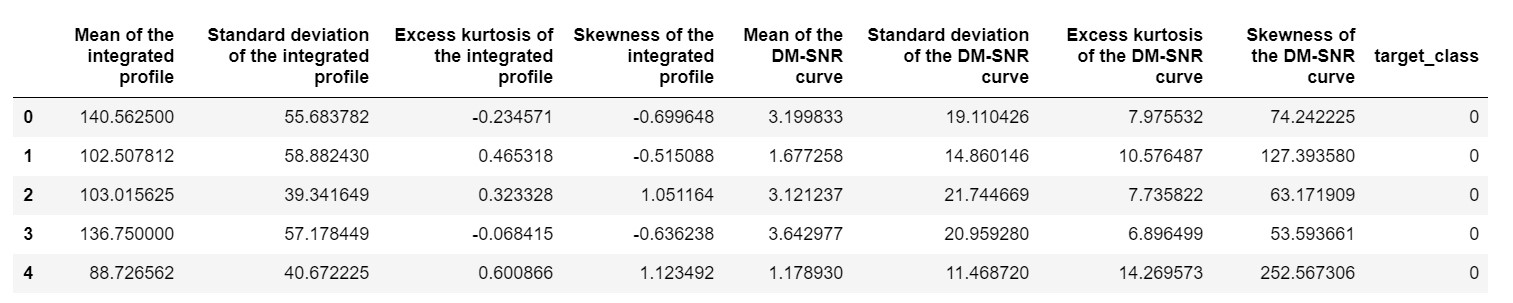
kita perlu menormalkan dataset agar tidak bias karena nilai ekstrim.

dari sklearn.preprocessing impor normalisasi

pulsar_data = normalisasi(pulsar_data)

Kami akan menggunakan kode standar, tetapi kali ini, kami menghitung waktu kedua perhitungan.

%%waktu

dari scipy.cluster.hierarchy import dendrogram, linkage

tertaut = tautan (data_pulsar, 'bangsal')

plt.figure(figsize=(10, 7))

dendrogram (tertaut)

plt.tampilkan()

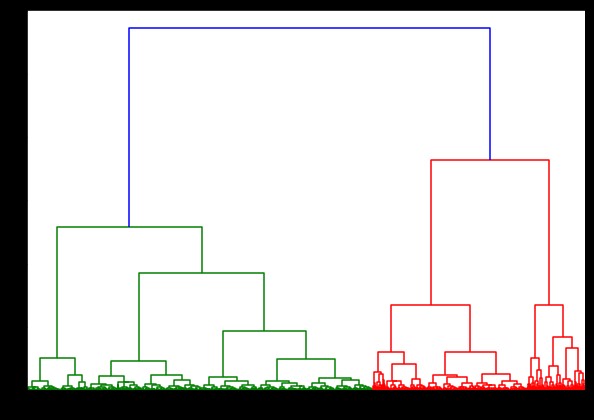
Waktu untuk menghasilkan dendrogram pada dataset IRIS adalah 6 detik. Waktu untuk menghasilkan dendrogram pada dataset HTRU2 adalah 13 menit 54 detik. Namun, ini tidak seberapa dibandingkan dengan perubahan prediksi karena keterkaitan yang berbeda, yang Anda amati dalam model yang dilatih dengan dataset HTRU2.

Mari kita ikuti prosedur yang sama seperti yang kita lakukan sebelumnya. Kali ini kami akan membuat prediksi pada setiap linkage.

Gambar berikut menunjukkan prediksi clustering dengan masing-masing linkage:

cluster = AgglomerativeClustering(n_clusters=2, affinity='euclidean', linkage='average') #serta lengkap, lingkungan dan tunggal

cluster.fit_predict(pulsar_data)

plt.figure(figsize=(10, 7))

plt.scatter(pulsar_data[:,1], pulsar_data[:,7], c=cluster.labels_)

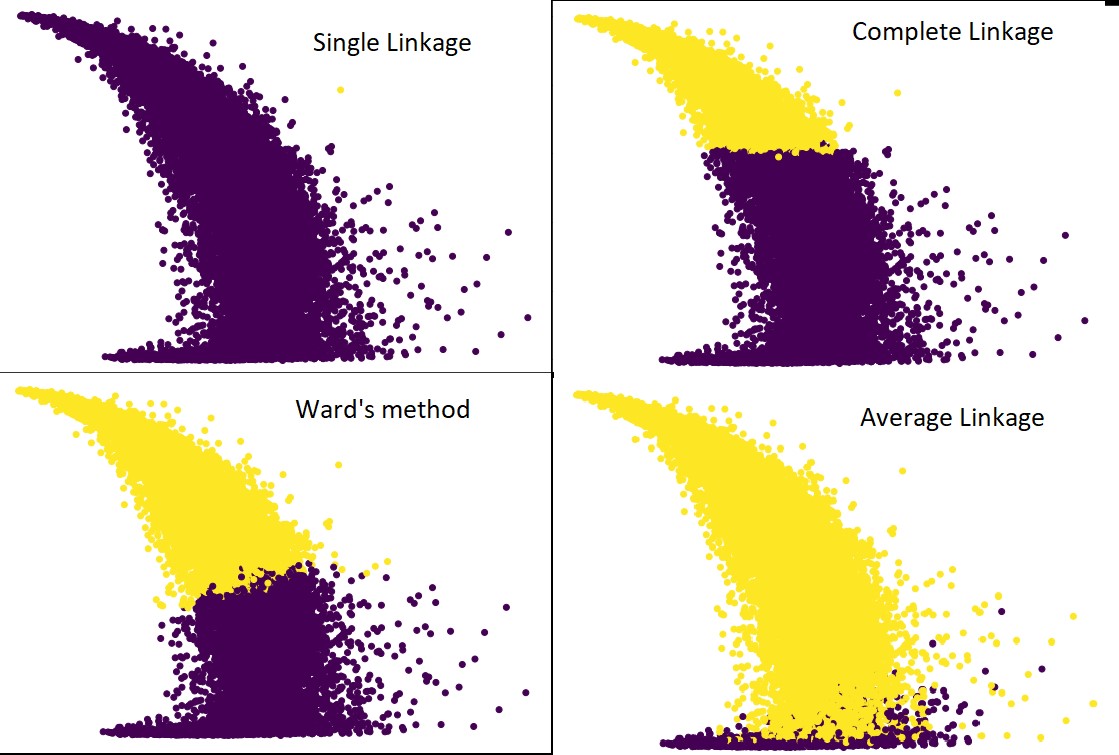
Ya, memang mengejutkan betapa berbedanya prediksi satu sama lain. Ini menunjukkan pentingnya matriks kedekatan dalam pengelompokan hierarkis.

Seperti yang Anda lihat, tautan tunggal mengambil hampir semua titik karena jarak minimum antara dua klaster menentukan metrik kedekatan. Ini membuatnya rentan terhadap data yang bising. Jika kita melihat keterkaitan yang lengkap, itu pasti membagi data menjadi dua cluster, tetapi mungkin telah memecahkan cluster besar hanya karena kedekatannya.

Hubungan rata-rata adalah trade-off antara keduanya. Ini kurang terpengaruh oleh kebisingan, tetapi masih dapat memecahkan kelompok besar, tetapi dengan kemungkinan yang lebih kecil. Dan, itu menangani klasifikasi dengan lebih baik.

Fungsi objektif seperti metode ward terkadang digunakan untuk menginisialisasi metode pengelompokan lain seperti K-means. Metode ini, seperti rata-rata-linkage, memiliki trade-off antara metode linkage tunggal dan lengkap. Fungsi objektif seperti metode ward terutama digunakan dalam solusi yang disesuaikan untuk mengurangi kemungkinan kesalahan klasifikasi. Dan, kami melihatnya berkinerja baik.

Pelajari: Analisis Cluster dalam Data Mining: Aplikasi, Metode & Persyaratan

Kompleksitas Ruang dan Waktu

Sekedar memberikan pemahaman, pertimbangkan cara metrik kedekatan didefinisikan dan dihitung. Metrik kedekatan membutuhkan untuk menyimpan jarak antara setiap pasangan cluster di dalam peta data. Itu membuat kompleksitas ruang: O(n2). Ini adalah jumlah yang besar. Untuk menempatkannya dalam perspektif, bayangkan kita memiliki 1.000.000 poin. Itu akan membawa kebutuhan ruang menjadi 1012 poin. Mengambil rata-rata kasar dan berat dengan memperkirakan ukuran satu titik sebagai byte, kami mendapatkan ukuran data pada 1TB. Dan ini perlu disimpan di RAM, bukan di hard drive.

Kedua, datangnya kompleksitas waktu. Untuk keperluan pemindaian matriks kedekatan pada setiap iterasi dan mengingat bahwa kita mengambil n langkah, kita mendapatkan kompleksitas sebagai O(n3). Ini mahal secara komputasi, terutama pada kumpulan data besar.

Dimungkinkan untuk menurunkannya ke O(n2logn), tetapi, itu masih terlalu mahal dibandingkan dengan algoritma pengelompokan lainnya, seperti K-means. Jika Anda ingin mempelajari lebih lanjut tentang menganalisis kompleksitas ruang dan waktu dari algoritme dan mengoptimalkan fungsi biaya, Anda dapat membuka Program di Ilmu Data dan Pembelajaran Mesin di tingkat atas.

Keterbatasan

• Kami telah membahas batasan pertama: Kompleksitas ruang dan waktu. Jelas bahwa pengelompokan hierarkis tidak menguntungkan dalam kasus kumpulan data besar. Bahkan jika kompleksitas waktu dikelola dengan mesin komputasi yang lebih cepat, kompleksitas ruang terlalu tinggi. Apalagi saat kita memuatnya di RAM. Dan, masalah kecepatan semakin meningkat ketika kami mengimplementasikan pengelompokan hierarkis dengan Python. Python lambat, dan jika menyangkut tugas-tugas besar, itu pasti akan menderita.
• Kedua, tidak ada teknik yang dioptimalkan dengan kedekatan. Jika kita melihat masing-masing memiliki banyak masalah dan keterbatasan, ini membuat mekanisme internal algoritma tidak dioptimalkan.
• Ketika kita melihat keputusan pengelompokan, mereka tidak dapat ditarik kembali. Artinya- setelah pengelompokan telah diterapkan untuk iterasi yang pasti, itu tidak akan berubah dalam iterasi lebih lanjut sampai penghentian. Jadi, jika karena ketidakakuratan struktural, algoritme, pada titik mana pun, memilih kluster yang salah untuk digabungkan atau dipecah, itu tidak dapat dibatalkan.
• Jika kita melihat lebih dekat pada algoritma, kita tidak memiliki fungsi tujuan yang jelas yang sedang diminimalkan. Dalam algoritma lain, ada fungsi tertentu yang kami coba optimalkan. Misalnya, dalam K-means kita memiliki fungsi biaya yang jelas yang kita minimalkan, yang tidak terjadi dengan pengelompokan hierarkis.

Lihat: 9 Algoritma Ilmu Data Teratas yang Harus Diketahui Setiap Ilmuwan Data

Kesimpulan

Meskipun ada batasan tertentu dalam hal kumpulan data besar, jenis algoritme pengelompokan ini menarik saat berurusan dengan kumpulan data skala kecil hingga menengah. Algoritma pengelompokan hierarkis di Python belum melihat banyak perkembangan dalam arsitektur atau skema karena kebutuhannya yang mengkhawatirkan akan kompleksitas ruang dan waktu.

Dan, memang benar bahwa saat ini, waktunya adalah Big Data. Itu berarti kami memang membutuhkan algoritme yang skalanya lebih baik. Namun, tetap saja, jika kita tidak yakin dengan jumlah klaster, atau kita perlu menyempurnakan analisis secara efisien, pengelompokan hierarkis dengan Python dapat menjadi pilihan yang memuaskan.

Dengan ini, Anda sekarang tahu cara menerapkan pengelompokan hierarkis dengan Python.

Untuk lebih memahami algoritme dan aplikasi metode semacam itu dalam Pembelajaran Mesin dan Ilmu Data, lihat penawaran kursus oleh upGrad. Kami memiliki program kumulatif untuk setiap jalur karir yang ingin Anda ikuti.

Program-program tersebut dikuratori oleh para profesional papan atas serta para profesor di IIIT-B. Untuk informasi lebih lanjut, pergilah ke upGrad . Jika Anda ingin tahu tentang mempelajari ilmu data untuk menjadi yang terdepan dalam kemajuan teknologi yang serba cepat, lihat Program PG Eksekutif upGrad & IIIT-B dalam Ilmu Data.