การจัดกลุ่มตามลำดับชั้นใน Python [แนวคิดและการวิเคราะห์]

ด้วยการไหลของข้อมูลดิบที่เพิ่มขึ้นและความจำเป็นในการวิเคราะห์ แนวคิดของ การเรียนรู้แบบไม่มี ผู้ดูแล จึงเป็นที่นิยมเมื่อเวลาผ่านไป ใช้เพื่อดึงข้อมูลเชิงลึกจากชุดข้อมูลที่ประกอบด้วยข้อมูลที่ป้อนโดยไม่มีค่าเป้าหมายที่มีป้ายกำกับ ก่อนที่เราจะเริ่มพูด ถึงการ จัดกลุ่มตามลำดับชั้นใน Python และใช้อัลกอริธึมกับชุดข้อมูลต่างๆ ให้เราทบทวนแนวคิดพื้นฐานของคลัสเตอร์ก่อน

การทำคลัสเตอร์ส่วนใหญ่เกี่ยวข้องกับการจำแนกประเภทของข้อมูลดิบ ประกอบด้วยการจัดกลุ่มจุดข้อมูลต่างๆ เข้าด้วยกัน ซึ่งมีความคล้ายคลึงกันมากที่สุด กลุ่มเหล่านี้เรียกว่าคลัสเตอร์ ซึ่งสร้างขึ้นตามเมตริกความเหมือนหรือการจัดกลุ่มที่กำหนดไว้

บทนำ

การ จัดกลุ่มตามลำดับชั้น เกี่ยวข้องกับข้อมูลในรูปแบบของแผนผังหรือลำดับชั้นที่กำหนดไว้อย่างดี กระบวนการนี้เกี่ยวข้องกับการจัดการกับสองคลัสเตอร์พร้อมกัน อัลกอริธึมอาศัยเมทริกซ์ความเหมือนหรือระยะทางสำหรับการตัดสินใจทางคอมพิวเตอร์ ความหมายซึ่งสองคลัสเตอร์จะผสานหรือวิธีการแบ่งคลัสเตอร์ออกเป็นสองกลุ่ม เมื่อคำนึงถึงสองตัวเลือกนี้ เรามีการ จัดกลุ่มตามลำดับชั้น สอง ประเภท หากคุณเป็นมือใหม่และสนใจที่จะเรียนรู้เพิ่มเติมเกี่ยวกับวิทยาศาสตร์ข้อมูล ลองดูหลักสูตรวิทยาศาสตร์ข้อมูลของเราจากมหาวิทยาลัยชั้นนำ

แง่มุมที่สำคัญอย่างหนึ่งของอัลกอริทึมคือเมทริกซ์ความคล้ายคลึงกัน (หรือที่เรียกว่าเมทริกซ์ความใกล้ชิด) เนื่องจากอัลกอริธึมทั้งหมดดำเนินการตามนั้น มีวิธีการใกล้เคียงมากมายที่จะกล่าวถึงในบทความต่อไป

ประเภท

การจัดกลุ่มแบบลำดับชั้นมีสองประเภท:

1. การรวมกลุ่มแบบรวมกลุ่ม
2. การแบ่งกลุ่มแบบแบ่งกลุ่ม

ประเภทเป็นไปตามการทำงานพื้นฐาน: วิธีการพัฒนาลำดับชั้น Agglomerative เป็นตัวสร้างลำดับชั้นจากล่างขึ้นบน ในขณะที่การหารเป็นตัวสร้างลำดับชั้นจากบนลงล่าง

Agglomerative นำจุดทั้งหมดเป็นคลัสเตอร์เดี่ยวๆ แล้วรวมเข้าด้วยกันในการวนซ้ำแต่ละครั้ง สองครั้ง การแตกแยกเริ่มต้นโดยสมมติว่าข้อมูลทั้งหมดเป็นคลัสเตอร์เดียวและแบ่งออกจนกว่าทุกจุดจะกลายเป็นคลัสเตอร์เดี่ยว

ผลลัพธ์คือชุดของคลัสเตอร์ที่ซ้อนกันซึ่งสามารถรับรู้ได้ว่าเป็นแผนผังลำดับชั้น วิธีที่ดีที่สุดในการดูคือการแปลงโครงสร้างชุดเป็น dendrogram เพื่อดูลำดับชั้น

ต่อไปนี้ให้ตัวอย่างง่ายๆ ของ dendrogram เทียบกับการแสดงคลัสเตอร์:

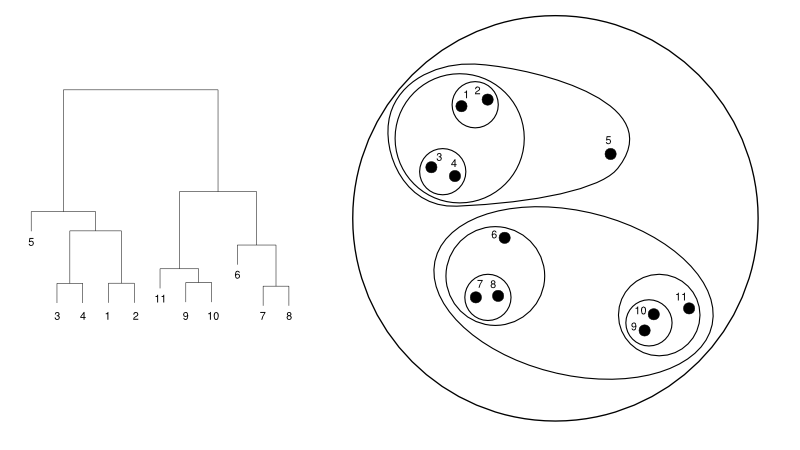
แหล่งที่มา

ที่นี่ การจัดกลุ่มอาจทำงานด้วยวิธีใดวิธีหนึ่ง แต่ผลลัพธ์จะเป็นชุดของคลัสเตอร์ จุดข้อมูล 1, 2, 3, 4, 5 และ 6 ถูกจัดกลุ่มเป็นสองจุดในแต่ละครั้ง และการจัดลำดับชั้นสามารถเห็นได้ในรูปด้านซ้าย ซึ่งเกี่ยวข้องกับ dendrogram ของสิ่งเดียวกัน การวิเคราะห์แบบเดียวกันนี้จะช่วยในการทำความเข้าใจการตัดสินใจของกลุ่ม

การกำหนดจำนวนคลัสเตอร์

คุณลักษณะที่มีประโยชน์มากที่สุดอย่างหนึ่งของอัลกอริทึมนี้คือ คุณสามารถแยกคลัสเตอร์ได้มากเท่าที่คุณต้องการเมื่ออัลกอริทึมสิ้นสุด มันค่อนข้างแตกต่างจากอัลกอริธึม K-means ในค่าเฉลี่ย K เราต้องผ่านไฮเปอร์พารามิเตอร์แบบไม่มีคลัสเตอร์ หมายความว่าเมื่ออัลกอริทึมเสร็จสิ้นการคำนวณ เราจะมีคลัสเตอร์จำนวนมาก แต่ถ้าเราต้องการคลัสเตอร์เพิ่มเติมในภายหลัง เราไม่สามารถปรับแต่งได้อย่างง่ายดาย ทางเลือกเดียวคือเปลี่ยนพารามิเตอร์และฝึกโมเดลอีกครั้ง

ในขณะที่เมื่อพูดถึงการทำคลัสเตอร์แบบลำดับชั้น คุณสามารถกำหนดจำนวนคลัสเตอร์ได้ในภายหลัง คุณสามารถใช้สองคลัสเตอร์ในตอนท้าย หากไม่พอใจ คุณอาจใช้ห้ากลุ่มที่เกิดขึ้นในขั้นตอนสุดท้ายหรือระดับที่สูงกว่า มันขึ้นอยู่กับคุณ. ดังนั้น เมื่อฝึกแล้ว คุณไม่จำเป็นต้องฝึกโมเดลใหม่เพื่อรับคลัสเตอร์มากหรือน้อย สามารถทำได้โดยเพียงแค่ ตัด dendrogram ในระดับที่คุณต้องการ

ในขณะที่เรามีแนวคิดลดลง ให้เราพูดถึงการทำงานของการ จัดกลุ่มตามลำดับ ชั้น ใน Python

สำหรับการทดลอง เราจะใช้ไลบรารี่ sci-kit เรียนรู้สำหรับอัลกอริธึมการจัดกลุ่ม นอกจากนี้เรายังจะใช้โมดูลคลัสเตอร์.dendrogram จาก SciPy เพื่อแสดงภาพและทำความเข้าใจกระบวนการ "ตัด" เพื่อจำกัดจำนวนคลัสเตอร์

นำเข้า numpy เป็น np

X = np.array([[3,5],

[12,9],

[13,17],

[14,14],

[60,52],

[55,63],

[69,59],])

มันจะมีลักษณะเช่นนี้ในพล็อต:

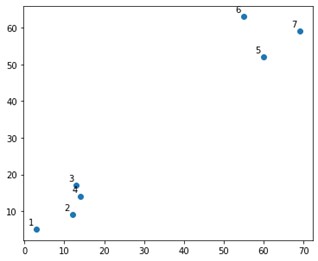
เราเห็นแล้วว่าเรามีคลัสเตอร์สุดท้ายสองกลุ่ม ที่มุมบนและมุมล่าง ให้เราดูว่าอัลกอริธึมสามารถคิดออกหรือไม่

เราจะใช้ฟังก์ชัน AgglomerativeClustering จากโมดูล sklearn.clustering

จาก sklearn.cluster นำเข้า AgglomerativeClustering

คลัสเตอร์ = AgglomerativeClustering(n_clusters=2, affinity='euclidean', linkage='ward')

cluster.fit_predict(X)

ที่นี่ เราระบุคลัสเตอร์ ซึ่งไม่ใช่ไฮเปอร์พารามิเตอร์ อย่างไรก็ตาม เราแค่ส่งผ่านเพื่อทำให้คลาสการทำนายชัดเจน เราจะใช้ฟังก์ชัน fit_predict เพื่อฝึกและทำนายคลาสบน X

สิ่งสำคัญคือต้องสังเกตว่าการทำคลัสเตอร์แบบรวมกลุ่มนั้นใช้มากกว่าการแบ่งแยกเนื่องจากดำเนินการได้ง่ายกว่า แนวคิดในการรวมคลัสเตอร์ตามเมทริกซ์ความใกล้เคียงนั้นดูง่ายกว่าการแบ่งคลัสเตอร์ออกเป็นสองกลุ่มโดยใช้กลไกบางอย่าง

อ่าน: Scikit-learn ใน Python: คุณสมบัติ ข้อกำหนดเบื้องต้น ข้อดี & ข้อเสีย

เพื่อให้เข้าใจอย่างชัดเจนถึงสิ่งที่เกิดขึ้นข้างต้น ให้ดูขั้นตอนที่เกี่ยวข้องกับอัลกอริทึม:

การทำงานของอัลกอริทึม

ต่อไปนี้เป็นขั้นตอนในการดำเนินการคลัสเตอร์แบบรวมกลุ่ม:

1. กำหนดจุดข้อมูลแต่ละจุดเป็นคลัสเตอร์
2. คำนวณตัววัดความใกล้เคียงเริ่มต้น
3. รวมสองคลัสเตอร์ที่ "ใกล้เคียงที่สุด" หรือคล้ายกันตามเมตริก
4. แก้ไขตัววัดความใกล้เคียงและทำซ้ำขั้นตอนที่สามจนกระทั่งเหลือคลัสเตอร์เดียว

ดังนั้น สิ่งเดียวที่ต้องเข้าใจคือผลกระทบของวิธีการใกล้เคียงที่แตกต่างกัน อย่างที่คุณทราบ ส่วนใหญ่มีวิธีความใกล้ชิดสี่ประเภทในการจัดกลุ่มแบบลำดับชั้น สิ่งนี้เรียกอีกอย่างว่าความคล้ายคลึงกันระหว่างคลัสเตอร์

วิธีการ (หรือการเชื่อมโยงตามที่กำหนดไว้ในรหัส) รวมถึง:

1. MIN หรือ Single linkage
2. MAX หรือการเชื่อมโยงที่สมบูรณ์
3. ความเชื่อมโยงเฉลี่ย
4. การเชื่อมโยงเซนทรอยด์
5. ฟังก์ชั่นพิเศษของฟังก์ชั่นวัตถุประสงค์

ผลลัพธ์ของสิ่งเดียวกันนั้นสามารถมองเห็นได้ง่ายโดยใช้ตัวเลือกการเชื่อมโยงในขณะที่สร้าง dendrograms

เพื่อให้เห็นภาพผลลัพธ์ของโมเดล เราแค่ต้องการข้อมูลโค้ดขนาดเล็กดังนี้:

plt.scatter(X[:,0],X[:,1], c=cluster.labels_, cmap='winter')

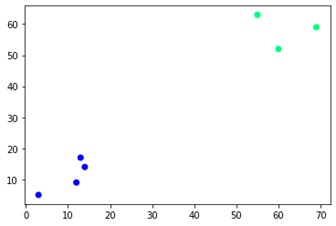
อย่างที่คุณเห็น มีกระจุกอยู่สองกลุ่มที่มุมตรงข้าม คุณอาจลองเล่นกับหมายเลขคลัสเตอร์และดูผลลัพธ์ที่ต่างออกไป ทุกสิ่งสามารถขับเคลื่อนได้ด้วยการตัดเดนโดรแกรม เพื่อให้เข้าใจว่า ให้เราเขียนตัวอย่างเล็กๆ น้อยๆ สำหรับการสร้างภาพการสร้างภาพ dendrograms

เราจะใช้ฟังก์ชัน dendrogram และ linkage จากโมดูล scipy.cluster.hierarchy ที่นี่ เรากำหนดการเชื่อมโยงที่เราต้องการใช้ เราจำเป็นต้องส่งผ่านวัตถุนั้นไปยังฟังก์ชัน dendrogram เพื่อสร้างลำดับชั้น

จาก scipy.cluster.hierarchy นำเข้า dendrogram, linkage

เชื่อมโยง = การเชื่อมโยง (X, 'สมบูรณ์')

labelList = ช่วง (1, 8)

plt.figure(figsize=(10, 7))

dendrogram (เชื่อมโยง

ปฐมนิเทศ='บน',

labels=labelList,

Distance_sort='มากไปน้อย',

show_leaf_counts=จริง)

plt.show()

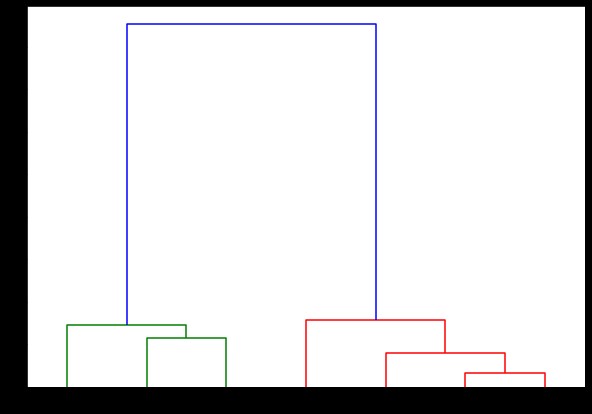
ที่นี่ คุณสามารถเห็นภาพว่าคลัสเตอร์เกิดขึ้นได้อย่างไรในการวนซ้ำแต่ละครั้ง ดังนั้น คุณสามารถ ตัด dendrogram ในระดับใดก็ได้ที่คุณต้องการ และคุณจะจบลงด้วยคลัสเตอร์จำนวนมากนั้น ดังนั้น เนื่องจากการสร้างลำดับชั้นนี้ คุณอาจเปลี่ยนแปลงจำนวนของคลัสเตอร์หลังจากเรียกใช้อัลกอริทึมและข้อมูลเพียงครั้งเดียว เป็นสิ่งที่ทำให้การจัดกลุ่มแบบลำดับชั้นได้เปรียบเหนืออัลกอริธึมอื่นๆ เช่น K-mean

ตอนนี้ ให้เรามาดูวิธีใช้การ จัดกลุ่มตามลำดับชั้นใน Python ในชุดข้อมูลที่ใช้กัน ทั่วไป : IRIS เราจะอ่านชุดข้อมูลจาก csv ในเครื่อง และเพียงแค่ดูคร่าวๆ ว่าชุดข้อมูลมีลักษณะอย่างไร และสิ่งที่เราจำเป็นต้องจัดประเภท

นำเข้า numpy เป็น np

นำเข้าแพนด้าเป็น pd

นำเข้า matplotlib.pyplot เป็น plt

%matplotlib แบบอินไลน์

ข้อมูล = pd.read_csv('iris.csv')

data.head()

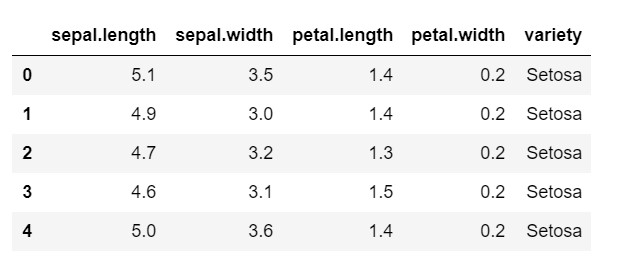
อย่างที่คุณเห็น ตัวแปรเป้าหมายคือคลาส 'วาไรตี้' รูปแบบนี้อยู่ในรูปแบบสตริงซึ่งจำเป็นต้องแปลงเป็นตัวเลข เนื่องจากโมเดลต้องใช้ป้ายกำกับที่เข้ารหัส ในการทำเช่นนี้ เราจะใช้ตัวเข้ารหัสฉลากจากไลบรารีประมวลผลก่อนการประมวลผลของ sklearn แบบง่ายๆ แปลงร่างเป็นตัวเลขได้

จากการประมวลผลล่วงหน้าการนำเข้า sklearn

le = การประมวลผลล่วงหน้า LabelEncoder()

le.fit(data['ความหลากหลาย'])

data['variety'] = le.transform(ข้อมูล['ความหลากหลาย'])

ตอนนี้ ถ้าเราสร้าง dendrogram เกี่ยวกับสิ่งนี้ เราจะพบการวนซ้ำและแผนที่ต่างๆ นี่คือลักษณะที่ปรากฏด้วยการเชื่อมโยงเดียว หากเราใช้โค้ดเดียวกันและรันด้วยการเชื่อมโยงแบบสมบูรณ์หรือแบบเซนทรอยด์ dendrograms จะแตกต่างกันเล็กน้อย ตรรกะยังคงเหมือนเดิม แต่การเชื่อมโยงที่แตกต่างกันจะส่งผลต่อลำดับของการควบรวมคลัสเตอร์อย่างแน่นอน

จาก scipy.cluster.hierarchy นำเข้า dendrogram, linkage

เชื่อมโยง = เชื่อมโยง (ข้อมูล 'วอร์ด')

plt.figure(figsize=(10, 7))

เดนโดรแกรม (เชื่อมโยง)

plt.show()

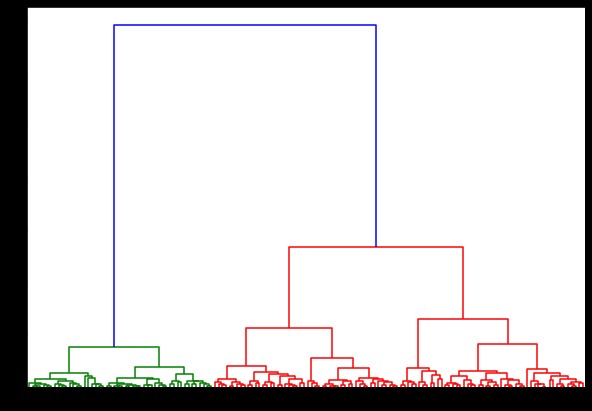
ตอนนี้ เมื่อใช้คลัสเตอร์บนชุดข้อมูล เราจะใช้การเชื่อมโยงสองแบบที่แตกต่างกัน และคุณจะเห็นได้อย่างชัดเจนว่าจริงๆ แล้วมีความแตกต่างกันอย่างไรในขณะกำหนดคลัสเตอร์ ดังที่เราได้เห็นจากตัวเข้ารหัสป้ายกำกับว่าเรามี 3 คลาสที่แตกต่างกัน ดังนั้นเราอาจใช้ 3 คลัสเตอร์ในตอนแรก

จาก sklearn.cluster นำเข้า AgglomerativeClustering

คลัสเตอร์ = AgglomerativeClustering(n_clusters=3, affinity='euclidean', linkage='complete')

cluster.fit_predict (ข้อมูล)

plt.figure(figsize=(10, 7))

plt.scatter(data['sepal.length'], data['petal.length'], c=cluster.labels_)

ดังที่คุณเห็นจากรูปด้านบน ในการจำแนกประเภท 3 คลัสเตอร์ การเชื่อมโยงจะแสดงการเปลี่ยนแปลงที่มองเห็นได้ในการทำนาย ดูการเชื่อมโยงวอร์ดก่อน มันคาดการณ์ป้ายกำกับได้อย่างถูกต้องโดยกำหนดให้คลัสเตอร์ด้านบนกำหนดไว้ แม้ว่าจะมีค่าผสมกันเล็กน้อยในทั้งสองคลัสเตอร์ แต่เมื่อเราเห็นการเชื่อมโยงทั้งหมด มันจะแบ่งกลุ่มและแยกประเภทค่าบางค่าผิดพลาด

ดังที่เราทราบในวิธีระยะใกล้ การเชื่อมโยงโดยสมบูรณ์มักจะทำลายคลัสเตอร์ที่ใหญ่กว่า ดังที่เราเห็นด้านบน วิธีการของวอร์ดหรือวิธีการเชื่อมโยงแบบเดียวมีความเสี่ยงน้อยกว่าต่อปัญหาเหล่านี้ นี่สำหรับชุดข้อมูลอย่างง่าย ให้เราดูว่าอัลกอริธึมได้รับผลกระทบอย่างไรและได้รับผลกระทบจากชุดข้อมูลที่มีเสียงดัง

ชุดข้อมูลดังกล่าวชุดหนึ่งคือชุดข้อมูลการทำนายพัลซาร์หรือ ชุด ข้อมูล HTRU2 ชุดข้อมูลมีขนาดใหญ่ขึ้น เนื่องจากมีตัวอย่างประมาณ 18,000 ตัวอย่าง หากมองเห็นด้วยเปอร์สเปคทีฟ ML ชุดข้อมูลจะมีขนาดปกติหรือต่ำกว่านั้น แต่ค่อนข้างจะหนักกว่าชุดข้อมูล IRIS ความจำเป็นในการใช้งานชุดข้อมูลที่หลากหลายคือการวิเคราะห์ประสิทธิภาพของการ จัดกลุ่มตามลำดับ ชั้น ใน Python เพื่อให้เข้าใจวิธีการและประโยชน์ของการนำไปปฏิบัติอย่างชัดเจน

pulsar_data = pd.read_csv('pulsar_stars.csv')

pulsar_data.head()

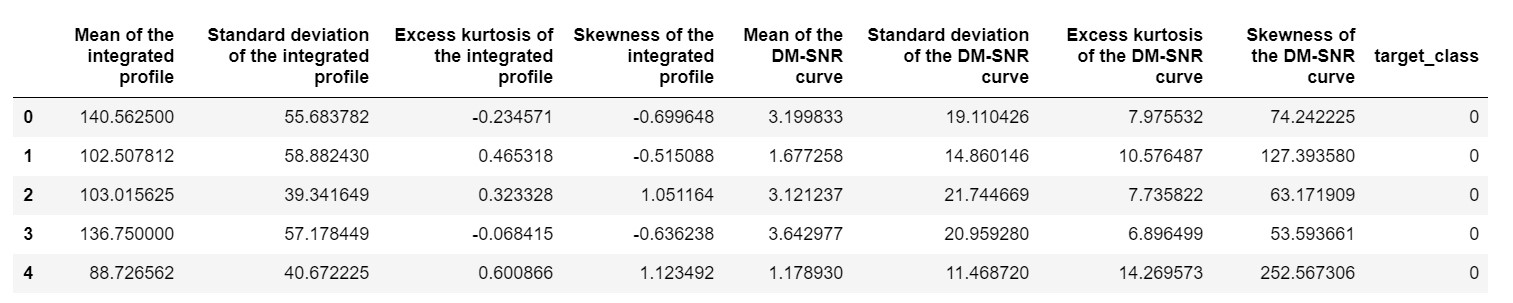
เราจะต้องทำให้ชุดข้อมูลเป็นปกติเพื่อไม่ให้มีอคติเนื่องจากค่าที่มากเกินไป

จาก sklearn.preprocessing การนำเข้าทำให้เป็นมาตรฐาน

pulsar_data = ทำให้เป็นมาตรฐาน (pulsar_data)

เราจะใช้รหัสมาตรฐาน แต่คราวนี้ เรากำลังจับเวลาการคำนวณทั้งสอง

%%เวลา

จาก scipy.cluster.hierarchy นำเข้า dendrogram, linkage

เชื่อมโยง = การเชื่อมโยง (pulsar_data, 'ward')

plt.figure(figsize=(10, 7))

เดนโดรแกรม (เชื่อมโยง)

plt.show()

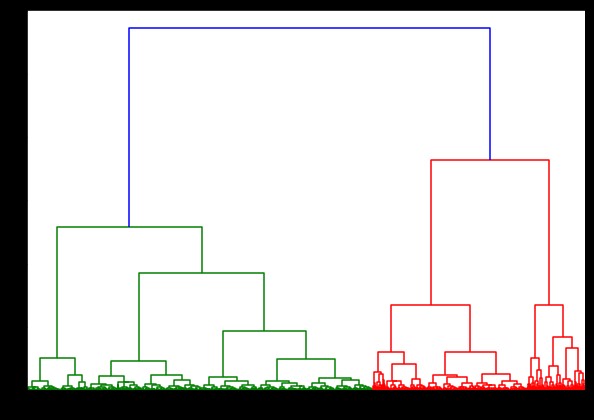
ระยะเวลาในการสร้าง dendrogram บนชุดข้อมูล IRIS คือ 6 วินาที ระยะเวลาสำหรับการสร้าง dendrogram บนชุดข้อมูล HTRU2 คือ 13 นาที 54 วินาที แต่สิ่งนี้ไม่ได้เทียบกับการเปลี่ยนแปลงในการคาดการณ์เนื่องจากการเชื่อมโยงที่แตกต่างกัน ซึ่งคุณสังเกตเห็นในแบบจำลองที่ฝึกด้วยชุดข้อมูล HTRU2

ให้เราทำตามขั้นตอนเดียวกับที่เราทำก่อนหน้านี้ คราวนี้เราจะทำการทำนายในทุกการเชื่อมโยง

รูปต่อไปนี้แสดงการคาดการณ์ของการจัดกลุ่มด้วยการเชื่อมโยงแต่ละรายการ:

คลัสเตอร์ = AgglomerativeClustering(n_clusters=2, affinity='euclidean', linkage='average') #รวมทั้งสมบูรณ์ วอร์ดและเดี่ยว

cluster.fit_predict (pulsar_data)

plt.figure(figsize=(10, 7))

plt.scatter(pulsar_data[:,1], pulsar_data[:,7], c=cluster.labels_)

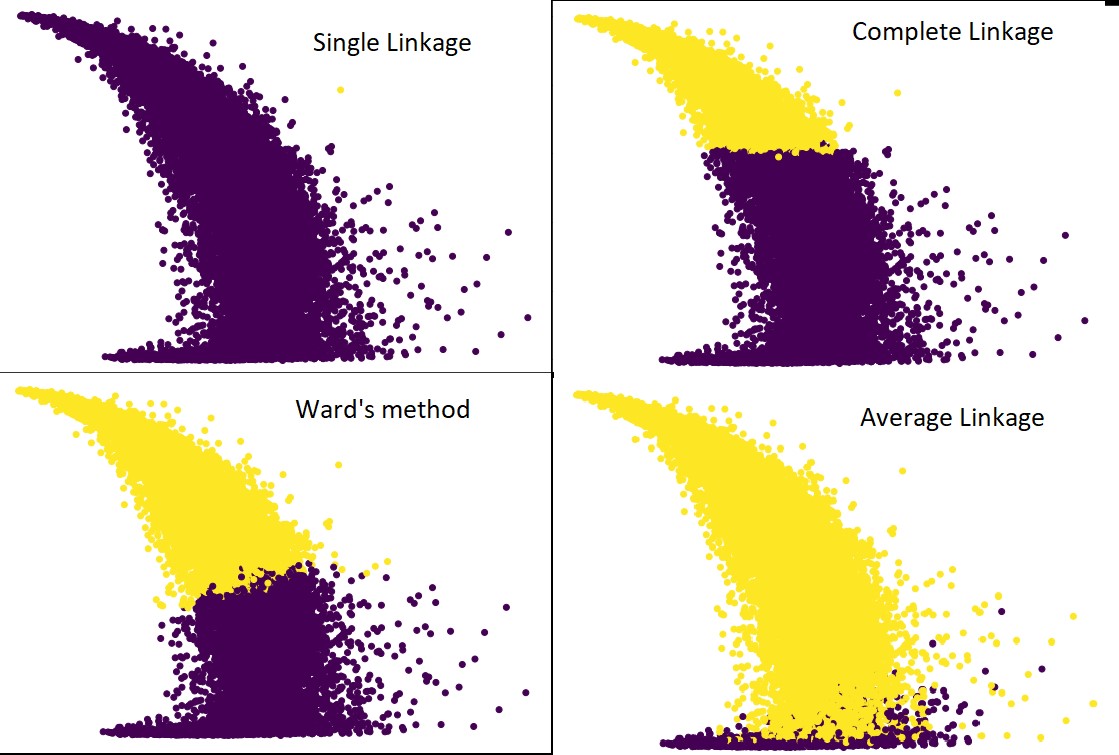
ใช่ น่าแปลกใจจริง ๆ ว่าคำทำนายต่างกันมากน้อยเพียงใด นี่แสดงให้เห็นความสำคัญของพร็อกซิมิตีเมทริกซ์ในการจัดกลุ่มแบบลำดับชั้น

อย่างที่คุณเห็น การเชื่อมโยงเพียงครั้งเดียวใช้จุดเกือบทั้งหมด เนื่องจากระยะห่างขั้นต่ำระหว่างสองคลัสเตอร์จะกำหนดเมตริกความใกล้เคียง ทำให้เสี่ยงต่อข้อมูลที่มีเสียงดัง หากเราเห็นการเชื่อมโยงที่สมบูรณ์ มันจะแบ่งข้อมูลออกเป็นสองกลุ่มอย่างแน่นอน แต่อาจทำให้คลัสเตอร์ขนาดใหญ่เสียหายได้เนื่องจากความใกล้ชิด

การเชื่อมโยงโดยเฉลี่ยเป็นการแลกเปลี่ยนระหว่างคนทั้งสอง ได้รับผลกระทบจากเสียงรบกวนน้อยกว่า แต่ก็ยังอาจทำลายกระจุกขนาดใหญ่ แต่มีโอกาสน้อยกว่า และจัดการการจำแนกประเภทได้ดีกว่า

ฟังก์ชันวัตถุประสงค์เช่นวิธีการของวอร์ดบางครั้งใช้สำหรับการเริ่มต้นวิธีการจัดกลุ่มอื่น ๆ เช่น K-mean วิธีนี้ เช่นเดียวกับการเชื่อมโยงเฉลี่ย มีการแลกเปลี่ยนระหว่างวิธีการเชื่อมโยงเดียวและสมบูรณ์ หน้าที่วัตถุประสงค์เช่นวิธีการของวอร์ดส่วนใหญ่จะใช้ในโซลูชันที่กำหนดเองเพื่อลดความน่าจะเป็นของการจัดประเภทผิด และเราเห็นว่ามันทำงานได้ดี

เรียนรู้: การวิเคราะห์คลัสเตอร์ในการขุดข้อมูล: แอปพลิเคชัน วิธีการ & ข้อกำหนด

ความซับซ้อนของเวลาและอวกาศ

เพื่อให้เกิดความเข้าใจ ให้พิจารณาวิธีการกำหนดและคำนวณตัววัดความใกล้เคียง ตัววัดความใกล้เคียงจำเป็นต้องเก็บระยะห่างระหว่างทุกคู่ของคลัสเตอร์ภายในแผนที่ข้อมูล ทำให้พื้นที่มีความซับซ้อน: O(n2) เป็นจำนวนมาก สมมติว่าเรามี 1,000,000 คะแนน นั่นจะทำให้ความต้องการพื้นที่ถึง 1,012 คะแนน การหาค่าเฉลี่ยแบบหยาบและหนักโดยการประมาณขนาดของจุดหนึ่งเป็นไบต์ เราได้ขนาดข้อมูลที่ 1TB และสิ่งนี้จะต้องเก็บไว้ใน RAM ไม่ใช่ในฮาร์ดไดรฟ์

ประการที่สอง ความซับซ้อนของเวลามา สำหรับความจำเป็นในการสแกนพร็อกซิมิตีเมทริกซ์ทุกครั้งที่วนซ้ำ และพิจารณาว่าเราทำตามขั้นตอน n ขั้น เราจะได้ความซับซ้อนเป็น O(n3) มีค่าใช้จ่ายในการประมวลผลสูง โดยเฉพาะชุดข้อมูลขนาดใหญ่

อาจเป็นไปได้ที่จะลดระดับลงไปที่ O(n2logn) แต่ก็ยังแพงเกินไปเมื่อเทียบกับอัลกอริธึมการจัดกลุ่มอื่นๆ เช่น K-mean หากคุณต้องการเรียนรู้เพิ่มเติมเกี่ยวกับการวิเคราะห์ความซับซ้อนของพื้นที่และเวลาของอัลกอริธึมและการปรับฟังก์ชันต้นทุนให้เหมาะสม คุณอาจไปที่โปรแกรมของ upGrad ใน Data Science และ Machine Learning

ข้อจำกัด

• เราได้พูดถึงข้อจำกัดแรกแล้ว: ความซับซ้อนของพื้นที่และเวลา เห็นได้ชัดว่าการจัดกลุ่มแบบลำดับชั้นไม่เอื้ออำนวยในกรณีของชุดข้อมูลขนาดใหญ่ แม้ว่าความซับซ้อนของเวลาจะได้รับการจัดการด้วยเครื่องคำนวณที่เร็วขึ้น แต่ความซับซ้อนของพื้นที่ก็สูงเกินไป โดยเฉพาะอย่างยิ่งเมื่อเราโหลดมันในแรม และปัญหาเรื่องความเร็วก็เพิ่มมากขึ้นเมื่อเรานำการ จัดกลุ่มแบบลำดับชั้นไปใช้ใน Python Python ทำงานช้า และหากกังวลเรื่องงานใหญ่ งานนั้นจะต้องทนทุกข์ทรมานอย่างแน่นอน
• ประการที่สอง ไม่มีเทคนิคที่เหมาะสมกับความใกล้ชิด หากเราเห็นว่าแต่ละปัญหามีปัญหาและข้อจำกัดหลายประการ จะทำให้กลไกภายในของอัลกอริทึมไม่มีประสิทธิภาพสูงสุด
• เมื่อเราพิจารณาการตัดสินใจของคลัสเตอร์ การตัดสินใจนั้นไม่สามารถหดได้ ความหมาย- เมื่อมีการใช้คลัสเตอร์สำหรับการวนซ้ำที่แน่นอน จะไม่มีการเปลี่ยนแปลงในการวนซ้ำเพิ่มเติมจนกว่าจะสิ้นสุด ดังนั้น หากเนื่องจากความไม่ถูกต้องของโครงสร้าง อัลกอริธึม เลือกคลัสเตอร์ที่ไม่ถูกต้องเพื่อรวมหรือแยก ณ จุดใดก็ตาม จะไม่สามารถเพิกถอนได้
• หากเราพิจารณาอัลกอริธึมอย่างใกล้ชิด เราจะไม่มีฟังก์ชันวัตถุประสงค์ที่ชัดเจนซึ่งกำลังถูกย่อให้เล็กสุด ในอัลกอริธึมอื่นๆ มีฟังก์ชันที่แน่นอนซึ่งเราพยายามปรับให้เหมาะสม ตัวอย่างเช่น ใน K-mean เรามีฟังก์ชันต้นทุนที่ชัดเจนซึ่งเราย่อให้เล็กสุด ซึ่งไม่ใช่กรณีที่มีการจัดกลุ่มแบบลำดับชั้น

เช็คเอาท์: อัลกอริธึมวิทยาศาสตร์ข้อมูล 9 อันดับแรกที่นักวิทยาศาสตร์ข้อมูลทุกคนควรรู้

บทสรุป

แม้ว่าจะมีข้อจำกัดบางอย่างเมื่อพูดถึงชุดข้อมูลขนาดใหญ่ แต่อัลกอริธึมการจัดกลุ่มประเภทนี้ก็น่าสนใจในขณะที่ต้องจัดการกับชุดข้อมูลขนาดเล็กถึงขนาดกลาง อัลกอริทึม การ จัดกลุ่มแบบลำดับชั้นใน Python ยังไม่เห็นการพัฒนามากนักในสถาปัตยกรรมหรือสคีมา เนื่องจากต้องใช้เวลาและความซับซ้อนของพื้นที่อย่างน่าตกใจ

และเป็นความจริงที่ขณะนี้ ถึงเวลาของบิ๊กดาต้า หมายความว่าเราต้องการอัลกอริทึมที่ปรับขนาดได้ดีขึ้น แต่ในกรณีที่เราไม่แน่ใจเกี่ยวกับจำนวนคลัสเตอร์ หรือเราต้องปรับแต่งการวิเคราะห์อย่างมีประสิทธิภาพ การ จัดกลุ่มแบบลำดับชั้นใน Python อาจเป็นทางเลือกที่น่าพอใจ

ด้วยเหตุนี้ คุณจึงรู้วิธีใช้งานการ จัดคลัสเตอร์แบบลำดับชั้นใน Python

สำหรับการทำความเข้าใจอัลกอริธึมและการประยุกต์ใช้วิธีการในการเรียนรู้ของเครื่องและวิทยาศาสตร์ข้อมูล ให้ดูที่หลักสูตรที่นำเสนอโดย upGrad เรามีโปรแกรมสะสมสำหรับเส้นทางอาชีพที่คุณต้องการติดตาม

โปรแกรมได้รับการดูแลโดยผู้เชี่ยวชาญชั้นนำและอาจารย์ที่ IIIT-B สำหรับข้อมูลเพิ่มเติม ไป ที่ upGrad หากคุณอยากรู้เกี่ยวกับการเรียนรู้วิทยาศาสตร์ข้อมูลเพื่อก้าวไปสู่ความก้าวหน้าทางเทคโนโลยีอย่างรวดเร็ว ลองดู Executive PG Program in Data Science ของ upGrad & IIIT-B