Clustering ierarhic în Python [Concepte și analiză]

Odată cu creșterea fluxului de date brute și nevoia de analiză, conceptul de învățare nesupravegheată a devenit popular în timp. Este folosit pentru a extrage informații din seturi de date constând din date de intrare fără valori țintă etichetate. Înainte de a începe să discutăm despre clusteringul ierarhic în Python și să aplicăm algoritmul pe diferite seturi de date, să revizuim ideea de bază a clusterării.

Clustering se ocupă în principal de clasificarea datelor brute. Acesta cuprinde gruparea diferitelor puncte de date împreună, care sunt cel mai asemănătoare între ele. Aceste grupuri sunt numite clustere, care sunt formate pe baza metricii de similaritate sau clustering definite.

Introducere

Gruparea ierarhică se ocupă de date sub forma unui arbore sau a unei ierarhii bine definite. Procesul implică tratarea a două grupuri în același timp. Algoritmul se bazează pe o matrice de similaritate sau distanță pentru deciziile de calcul. Adică ce două grupuri să fuzioneze sau cum să împarți un cluster în două. Având în vedere aceste două opțiuni, avem două tipuri de grupare ierarhică . Dacă sunteți începător și doriți să aflați mai multe despre știința datelor, consultați cursurile noastre de știință a datelor de la universități de top.

Unul dintre aspectele critice ale algoritmului este matricea de similaritate (cunoscută și sub denumirea de matrice de proximitate), deoarece întregul algoritm se desfășoară pe baza ei. Există multe metode de proximitate care sunt discutate mai departe în articol.

Tipuri

Gruparea ierarhică are două tipuri:

1. Aglomerare aglomerativă
2. Agruparea divizionară

Tipurile sunt după funcționalitatea fundamentală: modul de dezvoltare a ierarhiei. Aglomerativ este un generator de ierarhie de jos în sus, în timp ce divizor este un generator de ierarhie de sus în jos.

Agglomerative preia toate punctele ca clustere individuale și apoi le îmbină la fiecare iterație, câte două. Diviziunea începe prin a presupune că toate datele sunt un singur cluster și le împarte până când toate punctele devin clustere individuale.

Rezultatul este un set de clustere imbricate care pot fi percepute ca un arbore ierarhic. Cel mai bun mod de a-l vizualiza este de a converti structura setului într-o dendrogramă pentru a vizualiza ierarhia.

Următoarele oferă un exemplu simplu de dendrogramă față de reprezentarea cluster:

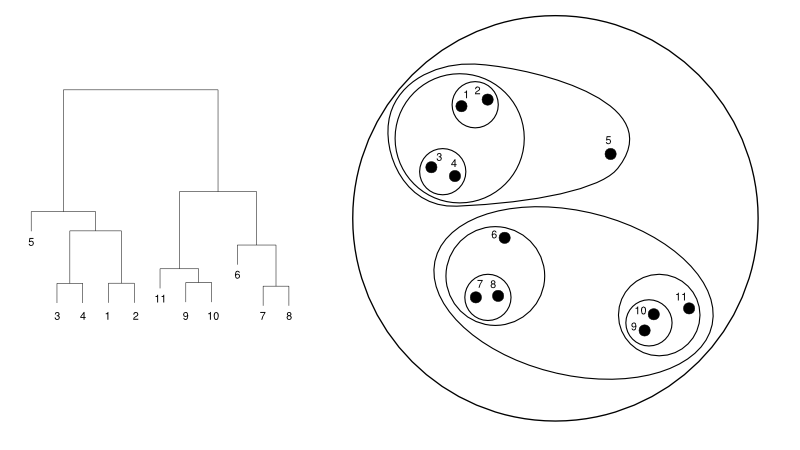
Sursă

Aici, gruparea poate funcționa în orice mod, dar rezultatul va fi o colecție de clustere. Punctele de date 1, 2, 3, 4, 5 și 6 sunt grupate în două simultan. Iar formarea ierarhiei poate fi văzută în figura din stânga, care se ocupă de dendrograma acesteia. Aceeași analiză ar ajuta la înțelegerea deciziei clusterelor.

Decizia numărului de clustere

Una dintre cele mai utile caracteristici ale acestui algoritm este că puteți extrage câte grupuri doriți odată ce algoritmul se termină. Este destul de diferit de algoritmul K-means. În K-means, trebuie să trecem hiperparametrul no-of-clusters. Înseamnă că odată ce algoritmul termină calculul, vom avea atât de multe clustere. Dar, dacă mai târziu avem nevoie de mai multe clustere, nu putem regla atât de ușor. Singura opțiune ar fi să schimbi parametrul și să antrenezi din nou modelul.

În timp ce, când vine vorba de gruparea ierarhică, puteți seta numărul de clustere mai târziu. Puteți lua două grupuri la sfârșit. Dacă nu sunteți mulțumit, puteți lua cele cinci grupuri formate la penultimul pas sau la nivelul superior. Depinde de tine. Prin urmare, odată antrenat, nu este nevoie să reantrenați modelul pentru a obține mai multe sau mai puține clustere. Poate fi realizat prin simpla tăiere a dendrogramei la nivelul dorit.

Întrucât avem conceptele jos, să discutăm despre funcționarea grupării ierarhice în Python .

Pentru experiment, vom folosi biblioteca sci-kit Learn pentru algoritmii de grupare. De asemenea, vom folosi modulul cluster.dendrogram de la SciPy pentru a vizualiza și înțelege procesul de „tăiere” pentru limitarea numărului de clustere.

import numpy ca np

X = np.array([[3,5],

[12,9],

[13,17],

[14,14],

[60,52],

[55,63],

[69,59],])

Ar arăta cam așa pe un complot:

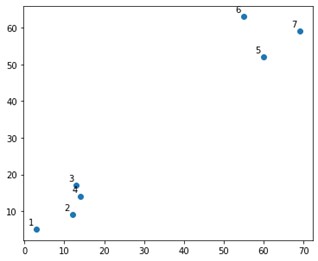
Ei bine, vedem că avem două grupuri definitive, în colțurile de sus și de jos. Să vedem dacă algoritmul poate înțelege sau nu.

Am folosi funcția AgglomerativeClustering din modulul sklearn.clustering.

din sklearn.cluster import AgglomerativeClustering

cluster = AgglomerativeClustering(n_clusters=2, afinity='euclidean', linkage='ward')

cluster.fit_predict(X)

Aici, specificăm clusterele, care nu este un hiperparametru. Cu toate acestea, îl trecem doar pentru a clarifica clasele de predicție. Am folosi funcția fit_predict pentru a antrena precum și a prezice clasele peste X.

Este important de remarcat că gruparea aglomerativă este mai folosită decât diviziunea, deoarece este mai simplu de executat. Ideea de a fuziona clustere bazate pe matrici de proximitate pare mai ușoară decât a împărți un cluster în două printr-un mecanism.

Citiți: Scikit-learn în Python: caracteristici, cerințe preliminare, avantaje și dezavantaje

Pentru a înțelege clar ce s-a întâmplat mai sus, priviți pașii implicați în algoritm:

Funcționarea algoritmului

Iată pașii pentru a executa clusteringul aglomerativ:

1. Definiți fiecare punct de date ca un cluster
2. Calculați metrica inițială de proximitate
3. Îmbinați două grupuri care sunt „cel mai apropiate” sau similare pe baza valorii
4. Revizuiți metrica de proximitate și repetați al treilea pas până când rămâne un singur cluster.

Deci, aici singurul lucru care rămâne de înțeles este impactul diferitelor metode de proximitate. După cum știți, în principal, există patru tipuri de metode de proximitate în gruparea ierarhică. Aceasta este cunoscută și sub denumirea de similitudine între clustere.

Metodele (sau legăturile, așa cum sunt definite în cod) includ:

1. Legătura MIN sau unică
2. Legătura MAX sau completă
3. Legătura medie
4. Legătura centroidă
5. Funcții exclusive ale funcțiilor obiective

Rezultatele pot fi vizualizate cu ușurință prin aplicarea opțiunii de conectare în timp ce se creează dendrogramele.

Pentru a vizualiza rezultatul modelului, avem nevoie doar de un mic fragment de cod, după cum urmează:

plt.scatter(X[:,0],X[:,1], c=cluster.labels_, cmap='iarna')

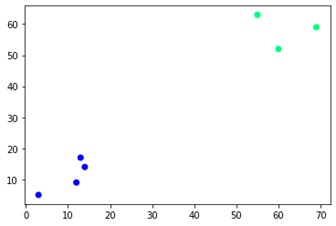
După cum puteți vedea, există două grupuri diferite în colțurile opuse. Puteți la fel de bine să vă jucați cu numerele de grup și să vedeți rezultate diferite. Întregul lucru poate fi condus prin tăierea dendrogramelor. Pentru a înțelege asta, să scriem un mic fragment pentru vizualizarea creării dendrogramelor.

Vom folosi funcțiile de dendrogramă și de legătură din modulul scipy.cluster.hierarchy. Aici definim legătura pe care dorim să o folosim. Trebuie să transmitem acel obiect la funcția dendrogramă pentru a genera ierarhia.

de la scipy.cluster.hierarchy import dendrogram, linkage

linked = linkage(X, 'complet')

labelList = interval (1, 8)

plt.figure(figsize=(10, 7))

dendrograma(legat,

orientare='sus',

labels=labelList,

distance_sort='descendent',

show_leaf_counts=Adevărat)

plt.show()

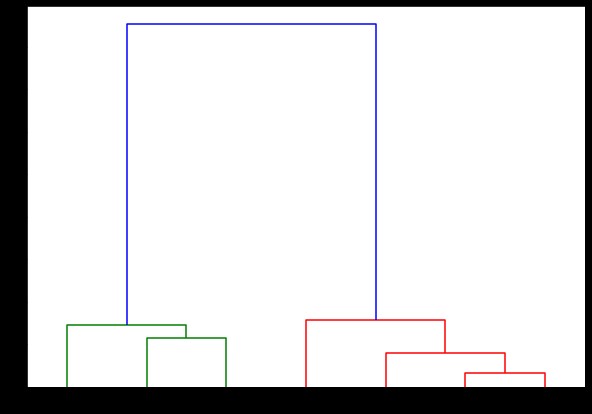
Aici, puteți vizualiza cum se formează clusterele la fiecare iterație. Deci, puteți tăia dendrograma la orice nivel doriți și veți ajunge cu atâtea grupuri. Prin urmare, datorită creării acestei ierarhii, puteți varia numărul de clustere după o singură trecere prin algoritm și date. Este ceea ce conferă grupării ierarhice un avantaj față de alți algoritmi precum K-means.

Acum, să ne uităm la modul de utilizare a grupării ierarhice în Python pe un set de date utilizat în mod obișnuit: IRIS . Am citi setul de date dintr-un csv local. și aruncați o privire asupra modului în care arată setul de date și a ceea ce trebuie să clasificăm.

import numpy ca np

importa panda ca pd

import matplotlib.pyplot ca plt

%matplotlib inline

date = pd.read_csv('iris.csv')

data.head()

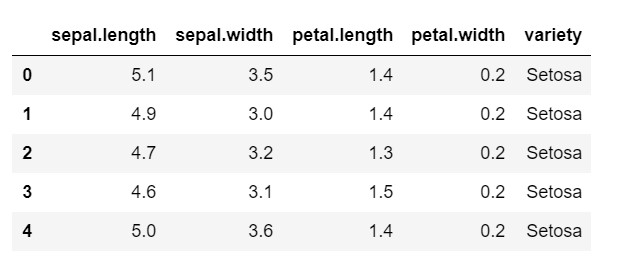
După cum puteți vedea, variabila țintă este clasa „varietate”. Acesta este în format șir care trebuie convertit în numere, deoarece modelul necesită etichete codificate. Pentru a face acest lucru, am folosi codificatorul de etichete din biblioteca de preprocesare a lui sklearn. O potrivire simplă și transformare pentru a le converti în numere.

din preprocesarea importului sklearn

le = preprocesare.LabelEncoder()

le.fit(date['varietate'])

data['variety'] = le.transform(data['variety'])

Acum, dacă creăm o dendrogramă pe aceasta, găsim diverse iterații și hărți. Așa arată cu o singură legătură. Dacă folosim același cod și îl rulăm cu o legătură completă sau centroid, dendrogramele ar diferi puțin. Logica rămâne aceeași, dar legăturile diferite ar afecta cu siguranță ordinea fuziunii clusterelor.

de la scipy.cluster.hierarchy import dendrogram, linkage

linked = linkage(date, „secție”)

plt.figure(figsize=(10, 7))

dendrogramă (legat)

plt.show()

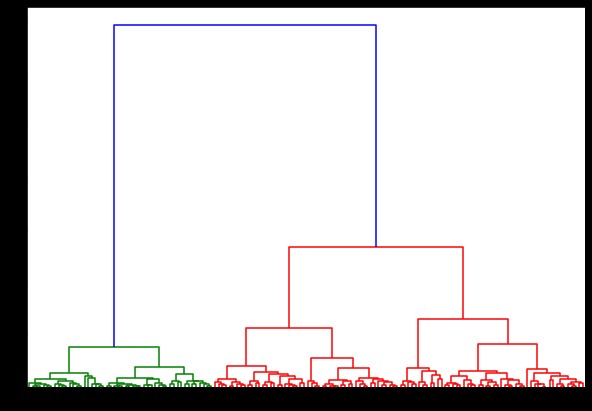
Acum, aplicând clustering pe setul de date, am folosi două legături diferite și veți vedea clar ce diferență are într-adevăr în timp ce definiți clusterele. După cum am văzut deja din codificatorul de etichete că avem 3 clase diferite, așa că putem aplica 3 clustere la început.

din sklearn.cluster import AgglomerativeClustering

cluster = AgglomerativeClustering(n_clusters=3, afinity='euclidean', linkage='complete')

cluster.fit_predict(date)

plt.figure(figsize=(10, 7))

plt.scatter(data['sepal.length'], data['petal.length'], c=cluster.labels_)

După cum puteți vedea din figura de mai sus, în clasificarea cu 3 grupuri, legăturile arată schimbări vizibile în predicție. Priviți mai întâi legătura dintre secții. Acesta prezice corect etichetele menținând grupul de mai sus definit, chiar dacă există o mică amestecare de valori în cele două grupuri. Dar, când vedem legătura completă, aceasta descompune clusterul și a clasificat greșit unele dintre valori.

După cum știm în metodele de proximitate, legătura completă tinde să rupă grupurile mai mari, așa cum putem vedea mai sus. Metoda secției sau metoda legăturii unice este mai puțin vulnerabilă la aceste probleme. Aceasta a fost pentru seturile de date simple. Să vedem cum algoritmul suferă și este afectat de unele seturi de date zgomotoase.

Un astfel de set de date este setul de date de predicție Pulsar sau setul de date HTRU2 . Setul de date este mai mare, deoarece conține aproximativ 18.000 de mostre. Dacă este văzut cu o perspectivă ML, setul de date are o dimensiune destul de normală sau chiar mai mică. Dar, comparativ, este mai greu decât setul de date IRIS. Necesitatea implementării pe un set de date variat este de a analiza performanța grupării ierarhice în Python . Pentru a înțelege clar modalitățile și avantajele implementărilor,

pulsar_data = pd.read_csv('pulsar_stars.csv')

pulsar_data.head()

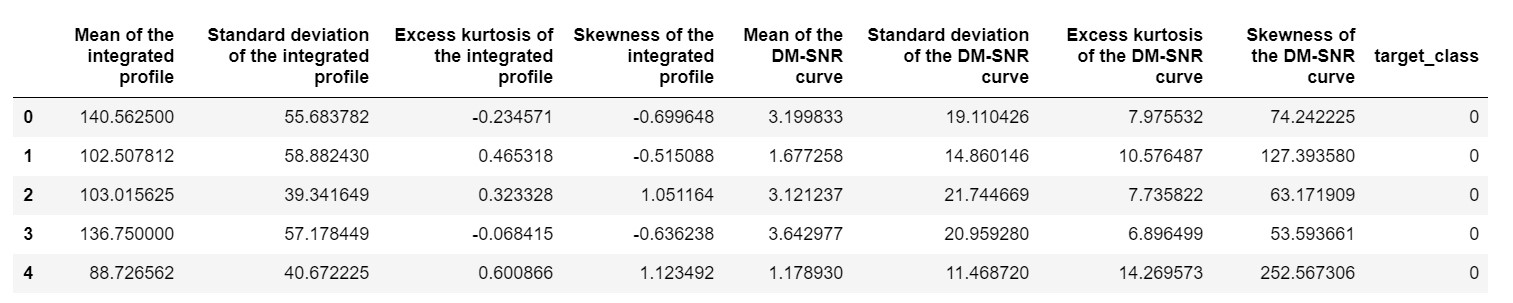
ar trebui să normalizăm setul de date, astfel încât să nu fie părtinit din cauza valorilor extreme.

din sklearn.preprocessing import normalize

pulsar_data = normalize(pulsar_data)

Am folosi codul standard, dar de data aceasta, cronometram ambele calcule.

%%timp

de la scipy.cluster.hierarchy import dendrogram, linkage

linked = linkage(pulsar_data, 'ward')

plt.figure(figsize=(10, 7))

dendrogramă (legat)

plt.show()

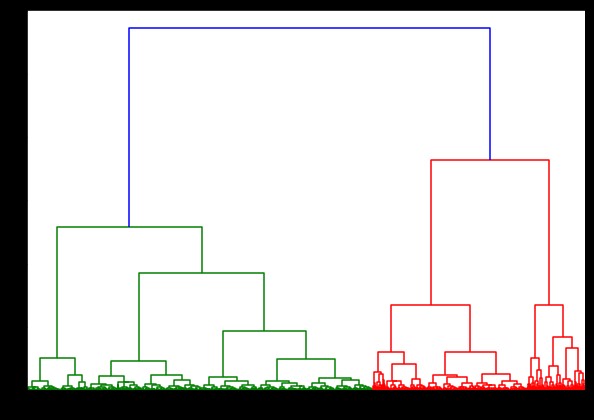
Timpul pentru generarea unei dendrograme pe setul de date IRIS a fost de 6 secunde. Timpul pentru generarea unei dendrograme pe setul de date HTRU2 a fost de 13 minute și 54 de secunde. Dar, acest lucru nu este nimic în comparație cu schimbarea predicțiilor din cauza diferitelor legături, pe care le observați în modelul antrenat cu setul de date HTRU2.

Să urmăm aceeași procedură ca și înainte. De data aceasta vom face predicții pentru fiecare legătură.

Următoarea figură arată predicțiile grupării cu fiecare legătură:

cluster = AgglomerativeClustering(n_clusters=2, afinity='euclidean', linkage='average') #precum complet,ward și single

cluster.fit_predict(pulsar_data)

plt.figure(figsize=(10, 7))

plt.scatter(pulsar_data[:,1], pulsar_data[:,7], c=cluster.labels_)

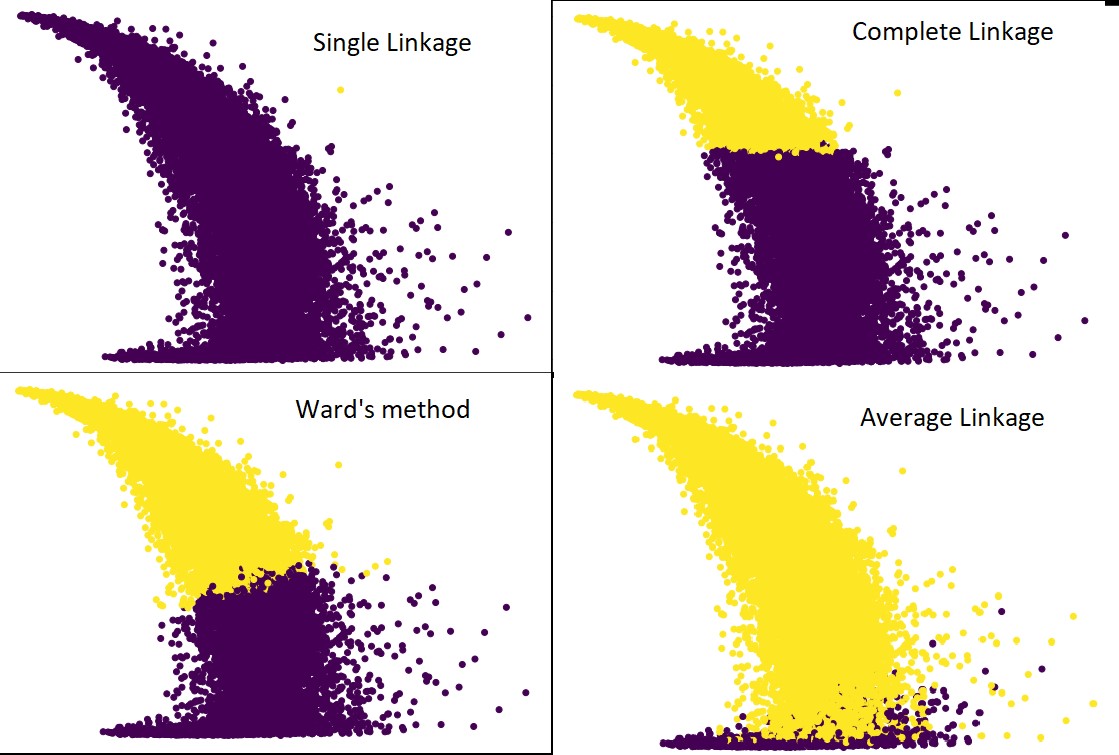
Da, este într-adevăr surprinzător cât de mult diferă predicțiile unele de altele. Aceasta arată importanța matricei de proximitate în gruparea ierarhică.

După cum puteți vedea, legătura unică preia aproape toate punctele, deoarece distanța minimă dintre două grupuri definește metrica de proximitate. Acest lucru îl face vulnerabil la datele zgomotoase. Dacă vedem legătura completă, cu siguranță împarte datele în două grupuri, dar este posibil să fi rupt clusterul mare doar din cauza proximității sale.

Legătura medie este un compromis între cele două. Este mai puțin afectat de zgomot, dar totuși poate sparge grupuri mari, dar cu o probabilitate mai mică. Și, se descurcă mai bine cu clasificarea.

Funcțiile obiective precum metoda secției sunt uneori folosite pentru inițializarea altor metode de grupare, cum ar fi K-means. Această metodă, la fel ca și legătura medie, are un compromis între metodele unice și complete. Funcțiile obiective precum metoda secției sunt utilizate în principal în soluții personalizate pentru a reduce probabilitatea de clasificare greșită. Și vedem că funcționează bine.

Aflați: Analiza clusterului în minarea datelor: aplicații, metode și cerințe

Complexitatea timpului și spațiului

Doar pentru a înțelege, luați în considerare modul în care este definită și calculată metrica de proximitate. Valoarea de proximitate necesită stocarea distanței dintre fiecare pereche de clustere în interiorul hărții de date. Face complexitatea spațiului: O(n2). Este un număr mare. Pentru a o pune în perspectivă, imaginați-vă că avem 1.000.000 de puncte. Acest lucru va duce necesarul de spațiu la 1012 puncte. Luând o medie aproximativă și grea prin aproximarea dimensiunii unui punct ca octet, obținem dimensiunea datelor la 1TB. Și acest lucru trebuie să fie stocat în RAM, nu pe hard disk.

În al doilea rând, vine complexitatea timpului. Pentru necesitatea scanării matricei de proximitate la fiecare iterație și având în vedere că luăm n pași, obținem complexitatea ca O(n3). Este costisitor din punct de vedere computațional, mai ales pe seturi mari de date.

Este posibil să o reduceți la O(n2logn), dar este totuși prea scumpă în comparație cu alți algoritmi de grupare, cum ar fi K-means. Dacă doriți să aflați mai multe despre analiza complexității în spațiu și timp a algoritmilor și despre optimizarea funcțiilor de cost, puteți merge la programele upGrad în știința datelor și învățarea automată.

Limitări

• Am discutat deja despre prima limitare: complexitatea spațiului și timpului. Este evident că clusteringul ierarhic nu este favorabil în cazul seturilor mari de date. Chiar dacă complexitatea timpului este gestionată cu mașini de calcul mai rapide, complexitatea spațiului este prea mare. Mai ales când îl încărcăm în RAM. Și problema vitezei crește și mai mult atunci când implementăm clusteringul ierarhic în Python. Python este lent și, dacă este vorba de sarcini mari, cu siguranță va avea de suferit.
• În al doilea rând, nu există o tehnică optimizată cu proximitatea. Dacă vedem că fiecare are mai multe probleme și limitări, acest lucru face ca mecanismul intern al algoritmului să fie neoptimizat.
• Când ne uităm la deciziile de grupare, acestea nu sunt retractabile. Înțeles - odată ce gruparea a fost aplicată pentru o iterație definită, nu va fi schimbată în iterații ulterioare până la terminare. Deci, dacă din cauza inexactităților structurale, algoritmul, în orice moment, alege grupuri greșite pentru a combina sau a împărți, este irevocabil.
• Dacă ne uităm îndeaproape la algoritm, nu avem o funcție obiectiv clară care este minimizată. În alți algoritmi, există o funcție definită pe care încercăm să o optimizăm. De exemplu, în K-means avem o funcție de cost clară pe care o minimizăm, ceea ce nu este cazul cu clusteringul ierarhic.

Consultați: Top 9 algoritmi de știință a datelor pe care fiecare cercetător de date ar trebui să-i cunoască

Concluzie

Chiar dacă există anumite limitări atunci când vine vorba de seturi de date mari, acest tip de algoritm de grupare este atrăgător atunci când se ocupă cu seturi de date la scară mică sau medie. Algoritmul de grupare ierarhică din Python nu a cunoscut o dezvoltare prea mare în arhitectură sau schemă din cauza nevoii sale alarmante de complexitate în timp și spațiu.

Și, este adevărat că chiar acum, este momentul Big Data. Înseamnă că avem nevoie de algoritmi care să se scaleze mai bine. Dar, totuși, în cazurile în care nu suntem siguri de numărul de clustere sau trebuie să rafinăm eficient analiza, gruparea ierarhică în Python poate fi o alegere satisfăcătoare.

Cu aceasta, acum știți cum să implementați clusteringul ierarhic în Python.

Pentru a înțelege mai multe astfel de algoritmi și aplicații ale metodelor în învățarea automată și știința datelor, aruncați o privire la ofertele de cursuri de la upGrad. Avem programe cumulate pentru oricare dintre căile de carieră pe care doriți să le urmați.

Programele sunt organizate de profesioniști de top, precum și de profesorii de la IIIT-B. Pentru mai multe informații, mergeți la upGrad . Dacă sunteți curios să învățați știința datelor pentru a fi în fața progreselor tehnologice rapide, consultați programul Executive PG în știința datelor de la upGrad și IIIT-B.