Clustering gerarchico in Python [Concetti e analisi]

Con l'aumento del flusso di dati grezzi e la necessità di analisi, il concetto di apprendimento non supervisionato è diventato popolare nel tempo. Viene utilizzato per trarre informazioni da set di dati costituiti da dati di input senza valori target etichettati. Prima di iniziare a discutere del clustering gerarchico in Python e di applicare l'algoritmo su vari set di dati, rivisitiamo l'idea di base del clustering.

Il clustering si occupa principalmente della classificazione dei dati grezzi. Comprende il raggruppamento di diversi punti dati, che sono molto simili tra loro. Questi gruppi sono chiamati cluster, che sono formati in base alla metrica di similarità o clustering definita.

introduzione

Il clustering gerarchico si occupa dei dati sotto forma di un albero o di una gerarchia ben definita. Il processo prevede la gestione di due cluster alla volta. L'algoritmo si basa su una matrice di similarità o distanza per le decisioni computazionali. Significato, quali due cluster unire o come dividere un cluster in due. Tenendo presenti queste due opzioni, abbiamo due tipi di clustering gerarchico . Se sei un principiante e sei interessato a saperne di più sulla scienza dei dati, dai un'occhiata ai nostri corsi di scienza dei dati delle migliori università.

Uno degli aspetti critici dell'algoritmo è la matrice di similarità (nota anche come matrice di prossimità), poiché l'intero algoritmo procede in base ad essa. Ci sono molti metodi di prossimità che sono discussi più avanti nell'articolo.

Tipi

Il clustering gerarchico ha due tipi:

1. Raggruppamento agglomerato
2. Raggruppamento divisivo

I tipi sono per la funzionalità fondamentale: il modo di sviluppare la gerarchia. Agglomerative è un generatore di gerarchie dal basso verso l'alto, mentre divisivo è un generatore di gerarchie dall'alto verso il basso.

Agglomerative prende tutti i punti come singoli cluster e poi li unisce ad ogni iterazione, due alla volta. Divisive inizia assumendo l'intero dato come un cluster e lo divide fino a quando tutti i punti diventano singoli cluster.

Il risultato è un insieme di cluster nidificati che possono essere percepiti come un albero gerarchico. Il modo migliore per visualizzarlo è convertire la struttura dell'insieme in un dendrogramma per visualizzare la gerarchia.

Di seguito viene fornito un semplice esempio di dendrogramma rispetto alla rappresentazione del cluster:

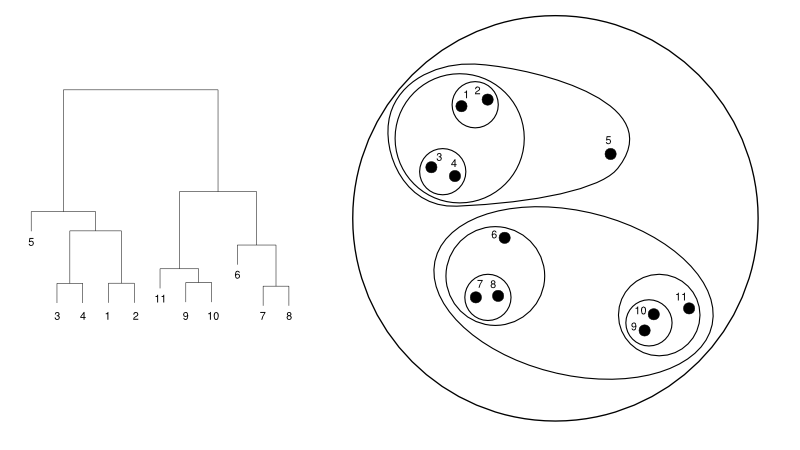
Fonte

Qui, il clustering può funzionare in entrambi i modi, ma il risultato sarà una raccolta di cluster. I punti dati 1, 2, 3, 4, 5 e 6 sono raggruppati in due alla volta. E la formazione della gerarchia è visibile nella figura a sinistra, che si occupa del dendrogramma della stessa. La stessa analisi aiuterebbe a comprendere la decisione dei cluster.

Decidere il numero di cluster

Una delle caratteristiche più utili di questo algoritmo è che puoi estrarre tutti i cluster che vuoi una volta terminato l'algoritmo. È abbastanza diverso dall'algoritmo K-mean. In K-mean, dobbiamo passare l'iperparametro no-of-cluster. Significa che una volta che l'algoritmo ha completato il calcolo, avremmo così tanti cluster. Ma, se abbiamo bisogno di più cluster in seguito, non possiamo sintonizzarci così facilmente. L'unica opzione sarebbe quella di modificare il parametro e addestrare nuovamente il modello.

Considerando che, quando si tratta del clustering gerarchico, è possibile impostare il numero di cluster in un secondo momento. Puoi prendere due cluster alla fine. Se non sei soddisfatto, puoi prendere i cinque gruppi formati al penultimo passaggio o al livello superiore. Dipende da te. Quindi, una volta addestrato, non è necessario riqualificare il modello per ottenere più o meno cluster. Può essere ottenuto semplicemente tagliando il dendrogramma al livello desiderato.

Poiché abbiamo i concetti in basso, discutiamo il funzionamento del clustering gerarchico in Python .

Per l'esperimento, utilizzeremo la libreria di apprendimento sci-kit per gli algoritmi di clustering. Utilizzeremmo anche il modulo cluster.dendrogram di SciPy per visualizzare e comprendere il processo di "taglio" per limitare il numero di cluster.

importa numpy come np

X = np.array([[3,5],

[12,9],

[13,17],

[14,14],

[60,52],

[55,63],

[69,59],])

Sembrerebbe qualcosa del genere su una trama:

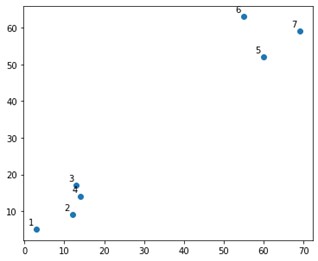
Bene, vediamo che abbiamo due gruppi definitivi, negli angoli superiore e inferiore. Vediamo se l'algoritmo riesce a capirlo o meno.

Useremmo la funzione AgglomerativeClustering dal modulo sklearn.clustering.

da sklearn.cluster import AgglomerativeClustering

cluster = AgglomerativeClustering(n_clusters=2, affinity='euclidea', linkage='ward')

cluster.fit_predict(X)

Qui specifichiamo i cluster, che non è un iperparametro. Tuttavia, lo passiamo solo per rendere chiare le classi di previsione. Useremmo la funzione fit_predict per addestrare e prevedere le classi su X.

È importante notare che il clustering agglomerato è più utilizzato di quello divisivo in quanto è più semplice da eseguire. L'idea di unire i cluster basati su matrici di prossimità sembra più facile che dividere un cluster in due tramite qualche meccanismo.

Leggi: Scikit-learn in Python: caratteristiche, prerequisiti, pro e contro

Per capire chiaramente cosa è successo sopra, guarda i passaggi coinvolti nell'algoritmo:

Funzionamento dell'algoritmo

Ecco i passaggi per eseguire il clustering agglomerato:

1. Definisci ogni punto dati come un cluster
2. Calcola la metrica di prossimità iniziale
3. Unisci due cluster che sono i "più vicini" o simili in base alla metrica
4. Rivedi la metrica di prossimità e ripeti il ​​terzo passaggio finché non rimane un singolo cluster.

Quindi, qui l'unica cosa che resta da capire è l'impatto dei diversi metodi di prossimità. Come sai, principalmente, ci sono quattro tipi di metodi di prossimità nel clustering gerarchico. Questa è anche nota come somiglianza tra cluster.

I metodi (o collegamento, come definito nel codice) includono:

1. Collegamento MIN o Singolo
2. Collegamento MAX o completo
3. Collegamento medio
4. Collegamento centroide
5. Funzioni esclusive delle funzioni obiettivo

I risultati dello stesso possono essere facilmente visualizzati applicando l'opzione di collegamento durante la creazione dei dendrogrammi.

Per visualizzare l'output del modello, abbiamo solo bisogno di un piccolo frammento di codice come segue:

plt.scatter(X[:,0],X[:,1], c=cluster.labels_, cmap='inverno')

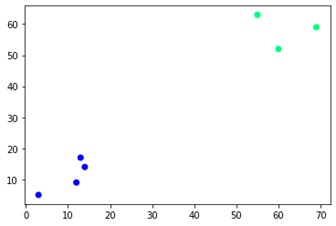
Come puoi vedere, ci sono due diversi gruppi agli angoli opposti. Puoi anche giocare con i numeri dei cluster e vedere risultati diversi. Il tutto può essere guidato tagliando i dendrogrammi. Per capirlo, scriviamo un piccolo snippet per la visualizzazione della creazione dei dendrogrammi.

Utilizzeremo le funzioni dendrogramma e collegamento dal modulo scipy.cluster.hierarchy. Qui, definiamo il collegamento che vogliamo utilizzare. Dobbiamo passare quell'oggetto alla funzione dendrogramma per generare la gerarchia.

da scipy.cluster.hierarchy import dendrogram, linkage

collegato = collegamento(X, 'completo')

labelList = intervallo(1, 8)

plt.figure(figsize=(10, 7))

dendrogramma(collegato,

orientamento='in alto',

etichette=Elenco etichette,

distance_sort='discendente',

show_leaf_counts=Vero)

plt.show()

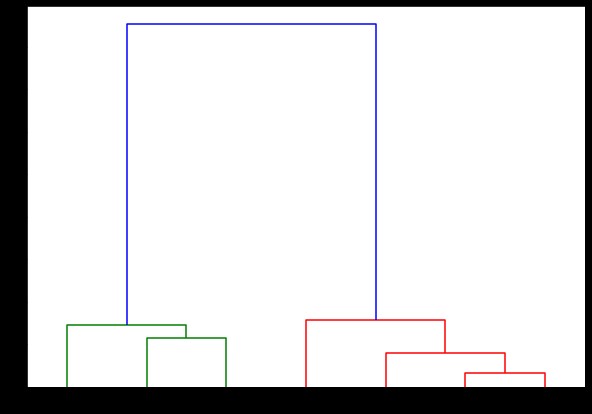
Qui puoi visualizzare come si formano i cluster ad ogni iterazione. Quindi, puoi tagliare il dendrogramma a qualsiasi livello desideri e ti ritroveresti con così tanti grappoli. Pertanto, a causa della creazione di questa gerarchia, è possibile variare il numero di cluster dopo una sola esecuzione dell'algoritmo e dei dati. È ciò che dà al clustering gerarchico un vantaggio su altri algoritmi come K-means.

Ora, diamo un'occhiata a come utilizzare il clustering gerarchico in Python su un set di dati di uso comune: IRIS . Leggeremmo il set di dati da un csv locale. e dai un'occhiata a come appare il set di dati e cosa dobbiamo classificare.

importa numpy come np

importa panda come pd

importa matplotlib.pyplot come plt

%matplotlib in linea

data = pd.read_csv('iris.csv')

data.head()

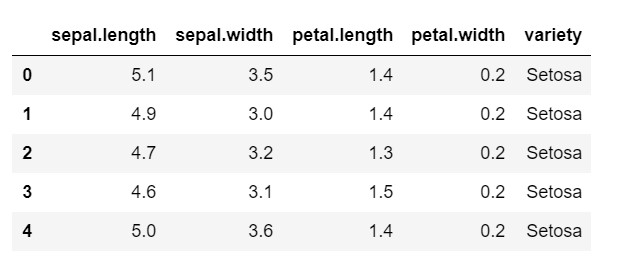
Come puoi vedere, la variabile target è la classe 'variety'. Questo è in formato stringa che deve essere convertito in numeri, poiché il modello richiede etichette codificate. Per fare ciò, utilizzeremo il codificatore di etichette dalla libreria di preelaborazione di sklearn. Un semplice adattamento e trasformazione per convertirli in numeri.

dalla preelaborazione dell'importazione di sklearn

le = preelaborazione.LabelEncoder()

le.fit(data['variety'])

data['variety'] = le.transform(data['variety'])

Ora, se creiamo un dendrogramma su questo, troviamo varie iterazioni e mappe. Ecco come appare con un unico collegamento. Se usiamo lo stesso codice e lo eseguiamo con collegamento completo o centroide, i dendrogrammi differirebbero leggermente. La logica rimane la stessa, ma collegamenti diversi influenzerebbero sicuramente l'ordine di fusione dei cluster.

da scipy.cluster.hierarchy import dendrogram, linkage

collegato = collegamento(dati, 'riparto')

plt.figure(figsize=(10, 7))

dendrogramma (collegato)

plt.show()

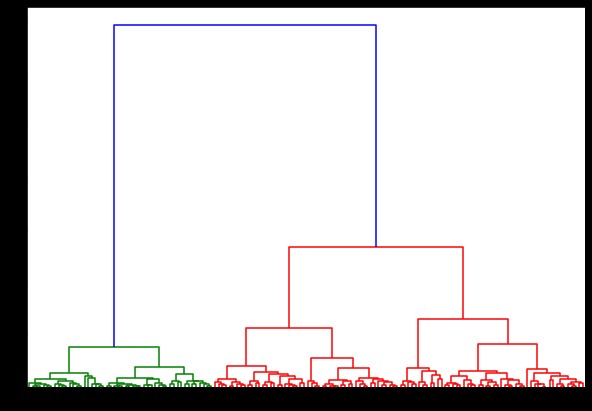
Ora, applicando il clustering sul set di dati, utilizzeremmo due diversi collegamenti e vedresti chiaramente quale differenza ha realmente durante la definizione dei cluster. Come abbiamo già visto dal codificatore di etichette che abbiamo 3 classi diverse, quindi potremmo inizialmente applicare 3 cluster.

da sklearn.cluster import AgglomerativeClustering

cluster = AgglomerativeClustering(n_clusters=3, affinity='euclidea', linkage='complete')

cluster.fit_predict(dati)

plt.figure(figsize=(10, 7))

plt.scatter(data['sepal.length'], data['petal.length'], c=cluster.labels_)

Come puoi vedere dalla figura sopra, nella classificazione a 3 cluster, i collegamenti mostrano cambiamenti visibili nella previsione. Guarda prima il collegamento del rione. Predice correttamente le etichette mantenendo definito il cluster sopra, anche se c'è una piccola confusione di valori nei due cluster. Ma, quando vediamo il collegamento completo, scompone il cluster e classifica erroneamente alcuni valori.

Come sappiamo nei metodi di prossimità, il collegamento completo tende a rompere i cluster più grandi, come possiamo vedere sopra. Il metodo del reparto o il metodo del collegamento unico è meno vulnerabile a questi problemi. Questo era per i semplici set di dati. Vediamo come l'algoritmo soffre ed è influenzato da alcuni set di dati rumorosi.

Uno di questi set di dati è il set di dati di previsione Pulsar o il set di dati HTRU2 . Il set di dati è più grande, poiché contiene circa 18.000 campioni. Se visto con una prospettiva ML, il set di dati ha dimensioni abbastanza regolari o addirittura inferiori. Ma, in confronto, è più pesante del set di dati IRIS. La necessità dell'implementazione su un set di dati vario è analizzare le prestazioni del clustering gerarchico in Python . Per comprendere chiaramente i modi e i vantaggi delle implementazioni,

pulsar_data = pd.read_csv('pulsar_stars.csv')

pulsar_data.head()

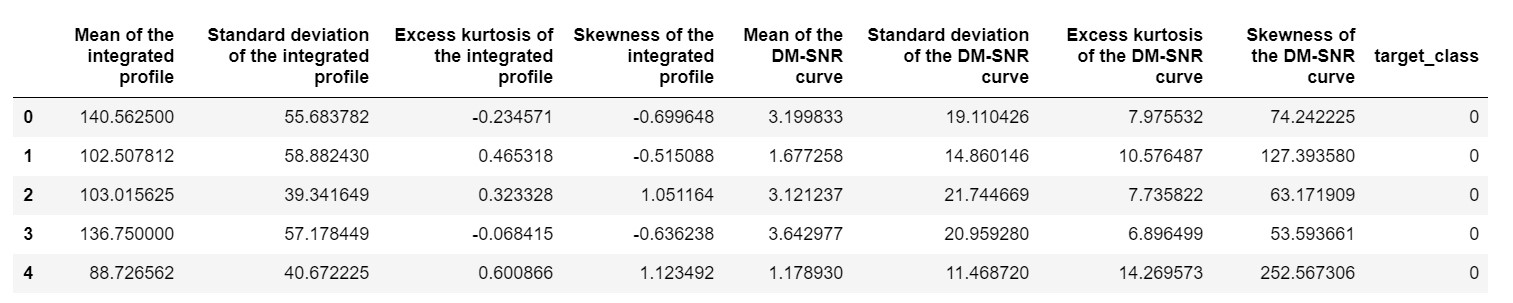
avremmo bisogno di normalizzare il set di dati in modo che non venga distorto a causa di valori estremi.

da sklearn.preprocessing import normalize

pulsar_data = normalizzare(pulsar_data)

Useremmo il codice standard, ma questa volta stiamo cronometrando entrambi i calcoli.

%%volta

da scipy.cluster.hierarchy import dendrogram, linkage

collegato = collegamento(pulsar_data, 'ward')

plt.figure(figsize=(10, 7))

dendrogramma (collegato)

plt.show()

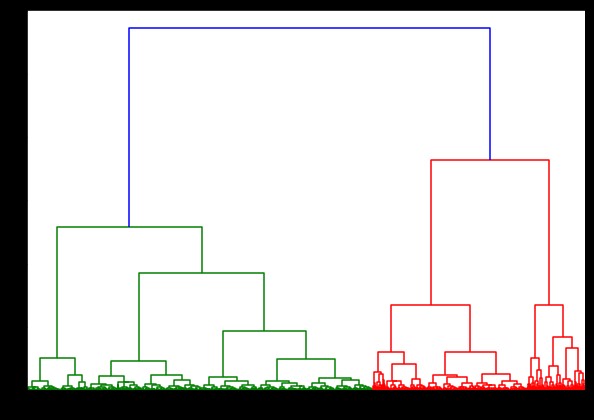
Il tempo per la generazione di un dendrogramma sul set di dati IRIS è stato di 6 secondi. Il tempo per la generazione di un dendrogramma sul set di dati HTRU2 era di 13 minuti e 54 secondi. Ma questo non è nulla in confronto al cambiamento nelle previsioni dovuto a diversi collegamenti, che si osservano nel modello addestrato con il set di dati HTRU2.

Seguiamo la stessa procedura di prima. Questa volta faremmo previsioni su ogni collegamento.

La figura seguente mostra le previsioni del clustering con ciascun collegamento:

cluster = AgglomerativeClustering(n_clusters=2, affinity='euclidea', linkage='media') #così come completo,ward e singolo

cluster.fit_predict(pulsar_data)

plt.figure(figsize=(10, 7))

plt.scatter(pulsar_data[:,1], pulsar_data[:,7], c=cluster.labels_)

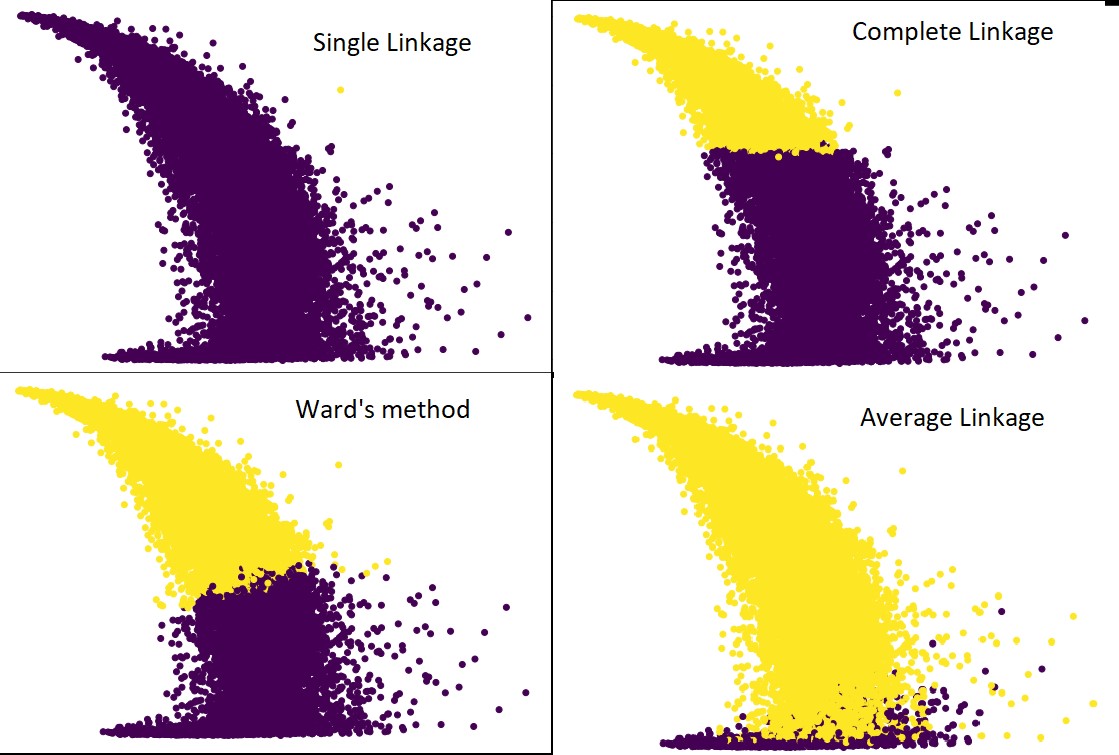
Sì, è davvero sorprendente quanto le previsioni differiscano l'una dall'altra. Ciò mostra l'importanza della matrice di prossimità nel clustering gerarchico.

Come puoi vedere, il collegamento singolo occupa quasi tutti i punti poiché la distanza minima tra due cluster definisce la metrica di prossimità. Questo lo rende vulnerabile ai dati rumorosi. Se vediamo il collegamento completo, divide definitivamente i dati in due cluster, ma potrebbe aver rotto il grande cluster solo a causa della sua vicinanza.

Il collegamento medio è un compromesso tra i due. È meno influenzato dal rumore, ma può comunque rompere grandi cluster, ma con una probabilità minore. E gestisce meglio la classificazione.

Funzioni obiettivo come il metodo del reparto vengono talvolta utilizzate per inizializzare altri metodi di raggruppamento come K-means. Questo metodo, proprio come il collegamento medio, ha un compromesso tra i metodi di collegamento singolo e completo. Le funzioni obiettive come il metodo del reparto sono utilizzate principalmente in soluzioni personalizzate per ridurre la probabilità di classificazione errata. E lo vediamo funzionare bene.

Impara: Cluster Analysis nel data mining: applicazioni, metodi e requisiti

Complessità temporale e spaziale

Giusto per dare un'idea, considera il modo in cui viene definita e calcolata la metrica di prossimità. La metrica di prossimità richiede di memorizzare la distanza tra ogni coppia di cluster all'interno della mappa dei dati. Rende la complessità dello spazio: O(n2). È un gran numero. Per metterlo in prospettiva, immagina di avere 1.000.000 di punti. Ciò porterà i requisiti di spazio a 1012 punti. Prendendo una media approssimativa e pesante approssimando la dimensione di un punto come byte, otteniamo la dimensione dei dati a 1 TB. E questo deve essere memorizzato nella RAM, non sul disco rigido.

In secondo luogo, arriva la complessità del tempo. Per la necessità di scansionare la matrice di prossimità ad ogni iterazione e considerando che facciamo n passi, otteniamo la complessità come O(n3). È computazionalmente costoso, specialmente su grandi set di dati.

Potrebbe essere possibile ridurlo a O(n2logn), ma è comunque troppo costoso rispetto ad altri algoritmi di clustering, come K-means. Se vuoi saperne di più sull'analisi della complessità spaziale e temporale degli algoritmi e sull'ottimizzazione delle funzioni di costo, puoi visitare i programmi di upGrad in Data Science e Machine Learning.

Limitazioni

• Abbiamo già discusso della prima limitazione: la complessità dello spazio e del tempo. È ovvio che il clustering gerarchico non è favorevole nel caso di big dataset. Anche se la complessità temporale è gestita con macchine computazionali più veloci, la complessità spaziale è troppo elevata. Soprattutto quando lo carichiamo nella RAM. E il problema della velocità aumenta ancora di più quando implementiamo il clustering gerarchico in Python. Python è lento e, se si tratta di grandi compiti, ne risentirà sicuramente.
• In secondo luogo, non esiste una tecnica ottimizzata con la prossimità. Se vediamo che ognuno ha più problemi e limitazioni, questo rende il meccanismo interno dell'algoritmo non ottimizzato.
• Quando osserviamo le decisioni di raggruppamento, non sono ritrattabili. Significato: una volta che il clustering è stato applicato per un'iterazione definita, non verrà modificato in ulteriori iterazioni fino alla fine. Quindi, se a causa di imprecisioni strutturali, l'algoritmo, in qualsiasi momento, sceglie i cluster sbagliati da combinare o dividere, è irrevocabile.
• Se osserviamo da vicino l'algoritmo, non abbiamo una chiara funzione obiettivo che viene ridotta al minimo. In altri algoritmi, c'è una funzione definita che cerchiamo di ottimizzare. Ad esempio, in K-mean abbiamo una chiara funzione di costo che riduciamo al minimo, il che non è il caso del clustering gerarchico.

Dai un'occhiata: i 9 migliori algoritmi di data science che ogni data scientist dovrebbe conoscere

Conclusione

Anche se ci sono alcune limitazioni quando si tratta di set di dati di grandi dimensioni, questo tipo di algoritmo di clustering è interessante quando si tratta di set di dati di piccola e media scala. L' algoritmo di clustering gerarchico in Python non ha visto molto sviluppo nell'architettura o nello schema a causa della sua allarmante necessità di complessità di tempo e spazio.

Ed è vero che in questo momento è il momento dei Big Data. Significa che abbiamo bisogno di algoritmi con una scalabilità migliore. Tuttavia, nei casi in cui non siamo sicuri del numero di cluster o abbiamo bisogno di perfezionare l'analisi in modo efficiente, il clustering gerarchico in Python può essere una scelta soddisfacente.

Con questo, ora sai come implementare il clustering gerarchico in Python.

Per comprendere meglio tali algoritmi e applicazioni dei metodi in Machine Learning e Data Science, dai un'occhiata alle offerte di corsi di upGrad. Abbiamo programmi cumulativi per tutti i percorsi di carriera che vuoi seguire.

I programmi sono curati dai migliori professionisti e dai professori di IIIT-B. Per ulteriori informazioni, vai a upGrad . Se sei curioso di imparare la scienza dei dati per essere all'avanguardia nei rapidi progressi tecnologici, dai un'occhiata al programma Executive PG in Data Science di upGrad & IIIT-B.