Unterstützung des Vektormaschinenalgorithmus beim maschinellen Lernen

Alles, was Sie über Support-Vector-Machine-Algorithmen wissen müssen

Die meisten Anfänger, wenn es um maschinelles Lernen geht, beginnen natürlich mit Regressions- und Klassifizierungsalgorithmen . Diese Algorithmen sind einfach und leicht zu befolgen. Es ist jedoch wichtig, über diese beiden maschinellen Lernalgorithmen hinauszugehen, um die Konzepte des maschinellen Lernens besser zu verstehen.

Beim maschinellen Lernen gibt es noch viel mehr zu lernen, was vielleicht nicht so einfach ist wie Regression und Klassifizierung, aber uns helfen kann, verschiedene komplexe Probleme zu lösen. Lassen Sie uns Ihnen einen solchen Algorithmus vorstellen, den Support Vector Machine Algorithm . Der Support-Vector-Machine-Algorithmus oder SVM-Algorithmus wird normalerweise als ein solcher maschineller Lernalgorithmus bezeichnet, der sowohl bei Regressions- als auch bei Klassifizierungsproblemen Effizienz und Genauigkeit liefern kann.

Wenn Sie davon träumen, eine Karriere im Bereich des maschinellen Lernens anzustreben, sollte die Support Vector Machine Teil Ihres Lernarsenals sein. Wir bei upGrad glauben daran, unsere Studenten mit den besten maschinellen Lernalgorithmen auszustatten, um mit ihrer Karriere zu beginnen. Folgendes kann Ihnen unserer Meinung nach beim Einstieg in den SVM-Algorithmus beim maschinellen Lernen helfen.

Was ist ein Support-Vector-Machine-Algorithmus?

SVM ist eine Art überwachter Lernalgorithmus, der im Jahr 2020 sehr populär geworden ist und dies auch in Zukunft bleiben wird. Die Geschichte von SVM reicht bis ins Jahr 1990 zurück; es stammt aus der statistischen Lerntheorie von Vapnik. SVM kann sowohl für Regressions- als auch für Klassifizierungsaufgaben verwendet werden; Es wird jedoch hauptsächlich zur Bewältigung von Klassifizierungsproblemen verwendet.

SVM ist ein diskriminativer Klassifikator, der Hyperebenen im N-dimensionalen Raum erstellt, wobei n die Anzahl der Merkmale in einem Datensatz ist, um die Unterscheidung zukünftiger Dateneingaben zu unterstützen. Klingt verwirrend, keine Sorge, wir werden es in einfachen Laienbegriffen verstehen.

Wie funktioniert ein Support-Vector-Machine-Algorithmus?

Bevor wir uns eingehend mit der Funktionsweise einer SVM befassen, wollen wir einige der wichtigsten Terminologien verstehen.

Hyperebene

Hyperebenen, die manchmal auch als Entscheidungsgrenzen oder Entscheidungsebenen bezeichnet werden, sind die Grenzen, die bei der Klassifizierung von Datenpunkten helfen. Die Seite der Hyperebene, auf die ein neuer Datenpunkt fällt, kann getrennt oder verschiedenen Klassen zugeordnet werden. Die Dimension der Hyperebene hängt von der Anzahl der Features ab, die einem Datensatz zugeordnet sind. Wenn der Datensatz 2 Features enthält, kann die Hyperebene eine einfache Linie sein. Wenn ein Datensatz 3 Features hat, dann ist die Hyperebene eine zweidimensionale Ebene.

Unterstützungsvektoren

Stützvektoren sind die Datenpunkte, die der Hyperebene am nächsten sind und ihre Position beeinflussen. Da diese Vektoren die Positionierung der Hyperebene beeinflussen, werden sie als Support-Vektoren bezeichnet und daher der Name Support Vector Machine Algorithm.

Rand

Vereinfacht ausgedrückt ist der Rand die Lücke zwischen der Hyperebene und den Stützvektoren. SVM wählt immer die Hyperebene, die den Spielraum maximiert. Je größer die Marge, desto höher ist die Genauigkeit der Ergebnisse. Es gibt zwei Arten von Rändern, die in SVM-Algorithmen verwendet werden , harte und weiche.

Wenn der Trainingsdatensatz linear trennbar ist, kann SVM einfach zwei parallele Linien auswählen, die den Randabstand maximieren; dies wird als harte Marge bezeichnet. Wenn der Trainingsdatensatz nicht vollständig linear getrennt ist, lässt die SVM eine gewisse Randverletzung zu. Es ermöglicht, dass einige Datenpunkte auf der falschen Seite der Hyperebene oder zwischen dem Rand und der Hyperebene bleiben, sodass die Genauigkeit nicht beeinträchtigt wird; dies wird als weicher Rand bezeichnet.

Für einen gegebenen Datensatz kann es viele mögliche Hyperebenen geben. Das Ziel von VSM ist es, den größtmöglichen Spielraum auszuwählen, um neue Datenpunkte in verschiedene Klassen zu klassifizieren. Wenn ein neuer Datenpunkt hinzugefügt wird, bestimmt die SVM, auf welche Seite der Hyperebene der Datenpunkt fällt. Basierend auf der Seite der Hyperebene, auf die der neue Datenpunkt fällt, klassifiziert SVM ihn dann in verschiedene Klassen.

Lesen Sie: Lineare Algebra für maschinelles Lernen: Kritische Konzepte, warum Lernen vor ML

Welche Arten von Support Vector Machines gibt es?

Basierend auf dem Trainingsdatensatz kann es zwei Arten von SVM-Algorithmen geben :

Lineare SVM

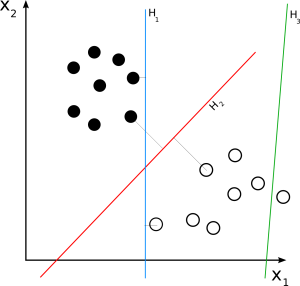
Quelle

Linear SVM wird für einen linear trennbaren Datensatz verwendet. Ein einfaches Beispiel aus der Praxis kann uns helfen, die Funktionsweise einer linearen SVM zu verstehen. Betrachten Sie einen Datensatz mit einem einzigen Merkmal, dem Gewicht einer Person. Die Datenpunkte können in zwei Klassen eingeteilt werden, fettleibig oder nicht fettleibig. Um Datenpunkte in diese beiden Klassen zu klassifizieren, kann SVM mit Hilfe der nächstgelegenen Unterstützungsvektoren eine Hyperebene mit maximalem Rand erstellen. Wenn jetzt ein neuer Datenpunkt hinzugefügt wird, erkennt die SVM die Seite der Hyperebene, auf die sie fällt, und klassifiziert die Person als fettleibig oder nicht.

Nichtlineare SVM

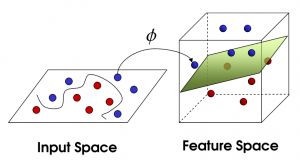
Quelle

Mit zunehmender Anzahl von Merkmalen wird es schwierig, den Datensatz linear zu trennen. Hier wird eine nichtlineare SVM verwendet. Wir können keine gerade Linie ziehen, um Datenpunkte zu trennen, wenn der Datensatz nicht linear trennbar ist. Um diese Datenpunkte zu trennen, fügt SVM also eine weitere Dimension hinzu. Die neue Dimension z kann als z = x2 + Y2 berechnet werden. Diese Berechnung hilft dabei, die Merkmale eines Datensatzes in linearer Form zu trennen, und dann kann SVM die Hyperebene erstellen, um Datenpunkte zu klassifizieren.

Wenn ein Datenpunkt in einen hochdimensionalen Raum transformiert wird, indem eine neue Dimension hinzugefügt wird, wird er leicht mit einer Hyperebene trennbar. Dies geschieht mit Hilfe des sogenannten Kernel-Tricks. Mit dem Kernel-Trick können SVM-Algorithmen nicht separierbare Daten in separierbare Daten umwandeln.

Was ist ein Kern?

Ein Kernel ist eine Funktion, die niedrigdimensionale Eingaben nimmt und sie in hochdimensionalen Raum umwandelt. Er wird auch als Tuning-Parameter bezeichnet, der hilft, die Genauigkeit der SVM-Ausgaben zu erhöhen. Sie führen einige komplexe Datentransformationen durch, um den nicht trennbaren Datensatz in einen trennbaren zu konvertieren.

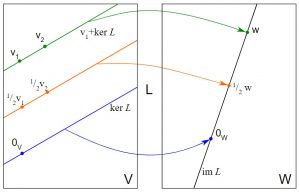
Quelle

Was sind die verschiedenen Arten von SVM-Kernels?

Linearer Kernel

Wie der Name schon sagt, wird der lineare Kernel für linear trennbare Datensätze verwendet. Es wird hauptsächlich für Datensätze mit einer großen Anzahl von Merkmalen verwendet, z. B. Textklassifizierung, bei der alle Alphabete ein neues Merkmal sind. Die Syntax des linearen Kernels lautet:

K(x, y) = Summe(x*y)

x und y in der Syntax sind zwei Vektoren.

Das Trainieren einer SVM mit einem linearen Kernel ist schneller als das Trainieren mit einem anderen Kernel, da nur der C-Regularisierungsparameter und nicht der Gammaparameter optimiert werden müssen.

Polynomialer Kern

Der Polynomkern ist eine allgemeinere Form des linearen Kerns, der beim Transformieren nichtlinearer Datensätze nützlich ist. Die Formel des Polynomkerns lautet wie folgt:

K(x, y) = (xT*y + c)d

Hier sind x und y zwei Vektoren, c ist eine Konstante, die einen Kompromiss zwischen Termen höherer und niedrigerer Dimension ermöglicht, und d ist die Ordnung des Kernels. Der Entwickler soll die Reihenfolge des Kernels manuell im Algorithmus festlegen.

Radialer Basisfunktionskern

Der radiale Basisfunktionskern, auch als Gaußscher Kern bezeichnet, ist ein weit verbreiteter Kern in SVM-Algorithmen zum Lösen von Klassifikationsproblemen. Es hat das Potenzial, Eingabedaten in unbestimmte hochdimensionale Räume abzubilden. Der radiale Basisfunktionskern kann mathematisch dargestellt werden als:

K(x, y) = exp(-gamma*sum(x – y2))

Hier sind x und y zwei Vektoren und Gamma ist ein Abstimmungsparameter im Bereich von 0 bis 1. Gamma wird manuell im Lernalgorithmus vordefiniert.

Die linearen, polynomialen und radialen Basisfunktionen unterscheiden sich in ihrem mathematischen Ansatz zum Treffen der Entscheidungen und der Genauigkeit der Hyperebenenerzeugung. Lineare und polynomiale Kernel verbrauchen weniger Zeit beim Training, bieten aber weniger Genauigkeit. Andererseits benötigt der radiale Basisfunktionskern mehr Zeit für das Training, liefert jedoch eine höhere Genauigkeit in Bezug auf die Ergebnisse.

Nun stellt sich die Frage, wie Sie auswählen, welcher Kernel für Ihren Datensatz verwendet werden soll. Ihre Entscheidung sollte ausschließlich von der Komplexität des Datensatzes und der Genauigkeit der gewünschten Ergebnisse abhängen. Natürlich möchte jeder Ergebnisse mit hoher Genauigkeit, aber es hängt auch davon ab, wie viel Zeit Sie für die Entwicklung der Lösung haben und wie viel Sie dafür aufwenden können. Außerdem bietet der radiale Basisfunktionskern im Allgemeinen eine höhere Genauigkeit, aber unter bestimmten Umständen können der lineare und der polynomische Kern gleich gut funktionieren.

Beispielsweise wird für linear trennbare Daten ein linearer Kernel genauso gut funktionieren wie ein radialer Basiskernel und dabei weniger Trainingszeit verbrauchen. Wenn Ihr Datensatz also linear trennbar ist, sollten Sie einen linearen Kernel wählen. Für nichtlineare Daten sollten Sie je nach Aufwand eine Polynom- oder Radialbasisfunktion wählen.

Was sind die Tuning-Parameter, die mit Kernels verwendet werden?

C-Regularisierung

Der C-Regularisierungsparameter akzeptiert Werte von Ihnen, um ein gewisses Maß an Fehlklassifizierung in jedem Trainingsdatensatz zuzulassen. Höhere C-Regularisierungswerte führen zu einer Hyperebene mit kleinem Rand und erlauben keine große Fehlklassifizierung. Niedrigere Werte hingegen führen zu einer hohen Marge und einer größeren Fehlklassifizierung.

Gamma

Der Gamma-Parameter definiert den Bereich der Unterstützungsvektoren, die sich auf die Positionierung der Hyperebene auswirken. Ein hoher Gammawert berücksichtigt nur nahegelegene Datenpunkte und ein niedriger Wert berücksichtigt weit entfernte Punkte.

Wie implementiert man den Support Vector Machine Algorithmus in Python?

Quelle

Da wir die grundlegende Vorstellung davon haben, was der SVM-Algorithmus ist und wie er funktioniert, wollen wir uns mit etwas Komplexerem befassen. Nun sehen wir uns die allgemeinen Schritte zum Implementieren und Ausführen des SVM-Algorithmus in Python an. Wir werden die Scikit-Learn-Bibliothek von Python verwenden, um zu lernen, wie der SVM-Algorithmus implementiert wird.

In erster Linie müssen wir alle notwendigen Bibliotheken wie Pandas und NumPy importieren, die zum Ausführen der SVM-Algorithmen erforderlich sind. Sobald wir alle Bibliotheken an Ort und Stelle haben, müssen wir den Trainingsdatensatz importieren. Als nächstes müssen wir unseren Datensatz analysieren. Es gibt mehrere Möglichkeiten, einen Datensatz zu analysieren.

Beispielsweise können wir die Dimensionen von Daten überprüfen, sie in Antwort- und erklärende Variablen unterteilen und KPIs festlegen, um unseren Datensatz zu analysieren. Nach Abschluss der Datenanalyse müssen wir den Datensatz vorverarbeiten. Wir sollten unseren Datensatz auf irrelevante, unvollständige und falsche Daten prüfen.

Jetzt kommt der Trainingsteil. Wir müssen unseren Algorithmus mit dem entsprechenden Kernel codieren und trainieren. Das Scikit-Learn enthält die SVM-Bibliothek, in der Sie einige eingebaute Klassen zum Trainieren von Algorithmen finden können. Die SVM-Bibliothek enthält eine SVC-Klasse, die den Wert für den Kerneltyp akzeptiert, den Sie zum Trainieren Ihrer Algorithmen verwenden möchten.

Dann rufen Sie die fit-Methode der SVC-Klasse auf, die Ihren Algorithmus trainiert, eingefügt als Parameter für die fit-Methode. Sie müssen dann die Vorhersagemethode der SVC-Klasse verwenden, um Vorhersagen für den Algorithmus zu treffen. Nachdem Sie den Vorhersageschritt abgeschlossen haben, müssen Sie den Algorithmus „classification_report“ und „confusion_matrix“ der Metrikbibliothek aufrufen, um Ihren Algorithmus auszuwerten und das Ergebnis anzuzeigen.

Was sind die Anwendungen des Support Vector Machine-Algorithmus?

SVM-Algorithmen haben Anwendungen für verschiedene Regressions- und Klassifizierungsherausforderungen. Einige der wichtigsten Anwendungen von SVM-Algorithmen sind:

• Text- und Hypertext-Klassifizierung
• Bildklassifizierung
• Klassifizierung von Satellitendaten wie Synthetic-Aperture Radar (SAR)
• Klassifizierung biologischer Substanzen wie Proteine
• Zeichenerkennung in handschriftlichem Text

Warum den Support-Vector-Machine-Algorithmus verwenden?

Der SVM-Algorithmus bietet verschiedene Vorteile wie:

• Effektiv bei der Trennung nichtlinearer Daten
• Hochpräzise in nieder- und höherdimensionalen Räumen
• Immun gegen das Problem der Überanpassung, da die Stützvektoren nur die Position der Hyperebene beeinflussen.

Check out: 6 Arten von Aktivierungsfunktionen in neuronalen Netzwerken, die Sie kennen müssen

Zusammenfassen

Wir haben uns den Support Vector Machine Algorithmus in diesem Artikel ausführlich angesehen. Wir haben etwas über den SVM-Algorithmus , seine Funktionsweise, seine Typen, Anwendungen, Vorteile und Implementierung in Python gelernt. Dieser Artikel gibt Ihnen einen grundlegenden Überblick über den SVM-Algorithmus und beantwortet einige Ihrer Fragen.

Aber es wird auch einige andere Fragen aufwerfen, z. B. woher der SVM-Algorithmus weiß, welche die richtige Hyperebene ist, welche anderen Bibliotheken in Python verfügbar sind und wo der Trainingsdatensatz zu finden ist. Wenn Sie mehr über maschinelles Lernen erfahren möchten, sehen Sie sich das PG-Diplom in maschinellem Lernen und KI von IIIT-B & upGrad an, das für Berufstätige konzipiert ist und mehr als 450 Stunden strenge Schulungen, mehr als 30 Fallstudien und Aufgaben bietet, IIIT- B-Alumni-Status, mehr als 5 praktische, praktische Abschlussprojekte und Jobunterstützung bei Top-Unternehmen.