機器學習中的支持向量機算法

關於支持向量機算法你需要知道的一切

大多數初學者，當談到機器學習時，自然會從回歸和分類算法開始。 這些算法簡單易懂。 但是，必須超越這兩種機器學習算法才能更好地掌握機器學習的概念。

機器學習還有很多東西要學，可能不像回歸和分類那麼簡單，但可以幫助我們解決各種複雜的問題。 讓我們向您介紹一種這樣的算法，即支持向量機算法。 支持向量機算法或SVM 算法通常被稱為一種這樣的機器學習算法，它可以為回歸和分類問題提供效率和準確性。

如果您夢想在機器學習領域從事職業，那麼支持向量機應該是您學習武器庫的一部分。 在upGrad ，我們相信為我們的學生提供最好的機器學習算法，以開始他們的職業生涯。 以下是我們認為可以幫助您從機器學習中的SVM 算法開始的內容。

什麼是支持向量機算法？

SVM 是一種監督學習算法，在 2020 年變得非常流行，並且在未來還會繼續流行。 SVM 的歷史可以追溯到 1990 年； 它來自 Vapnik 的統計學習理論。 SVM 可用於回歸和分類挑戰； 但是，它主要用於解決分類挑戰。

SVM 是一種判別分類器，它在 N 維空間中創建超平面，其中 n 是數據集中的特徵數，以幫助區分未來的數據輸入。 聽起來很混亂，別擔心，我們會用簡單的外行術語來理解它。

支持向量機算法如何工作？

在深入研究 SVM 的工作原理之前，讓我們先了解一些關鍵術語。

超平面

超平面，有時也稱為決策邊界或決策平面，是幫助對數據點進行分類的邊界。 新數據點所在的超平面一側可以被隔離或歸因於不同的類別。 超平面的維度取決於歸屬於數據集的特徵數量。 如果數據集有 2 個特徵，那麼超平面可以是一條簡單的線。 當一個數據集有 3 個特徵時，超平面就是一個二維平面。

支持向量

支持向量是最接近超平面並影響其位置的數據點。 由於這些向量影響超平面定位，因此它們被稱為支持向量，因此稱為支持向量機算法。

利潤

簡單地說，margin 就是超平面和支持向量之間的差距。 SVM 總是選擇最大化邊距的超平面。 邊際越大，結果的準確性就越高。 SVM 算法中使用兩種類型的邊距，硬邊距和軟邊距。

當訓練數據集線性可分時，SVM可以簡單地選擇兩條邊際距離最大化的平行線； 這稱為硬邊距。 當訓練數據集不是完全線性分離時，SVM 允許一些邊距違規。 它允許一些數據點停留在超平面的錯誤一側或邊緣和超平面之間，從而不影響準確性； 這稱為軟邊距。

給定數據集可能有許多可能的超平面。 VSM 的目標是選擇最大的邊距來將新數據點分類到不同的類別中。 添加新數據點時，SVM 會確定數據點落在超平面的哪一側。 基於新數據點所在的超平面的一側，SVM 然後將其分類為不同的類別。

閱讀：機器學習的線性代數：關鍵概念，為什麼要在機器學習之前學習

支持向量機的類型有哪些？

基於訓練數據集， SVM算法s可以有兩種類型：

線性支持向量機

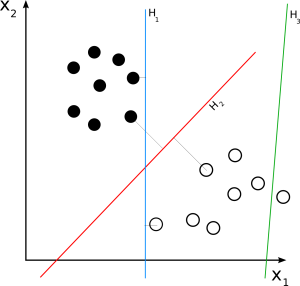
資源

線性 SVM 用於線性可分數據集。 一個簡單的真實示例可以幫助我們理解線性 SVM 的工作原理。 考慮一個具有單一特徵的數據集，即人的體重。 數據點可以被分為兩類，肥胖或不肥胖。 為了將數據點分為這兩類，SVM 可以在最近的支持向量的幫助下創建一個最大邊距超平面。 現在，每當添加一個新數據點時，SVM 都會檢測超平面的一側，它落在哪裡，並將此人分類為肥胖與否。

非線性支持向量機

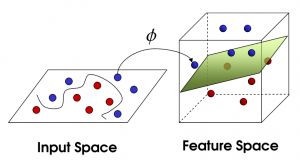
資源

隨著特徵數量的增加，線性分離數據集變得具有挑戰性。 這就是使用非線性 SVM 的地方。 當數據集不是線性可分的時，我們不能畫一條直線來分隔數據點。 因此，為了分離這些數據點，SVM 添加了另一個維度。 新維度 z 可以計算為 z = x2 + Y2。 這種計算將有助於以線性形式分離數據集的特徵，然後 SVM 可以創建超平面來對數據點進行分類。

當通過添加新維度將數據點轉換為高維空間時，它可以很容易地與超平面分離。 這是在所謂的內核技巧的幫助下完成的。 借助內核技巧， SVM 算法可以將不可分離的數據轉換為可分離的數據。

什麼是內核？

內核是一個函數，它接受低維輸入並將它們轉換為高維空間。 它也被稱為有助於提高 SVM 輸出準確性的調整參數。 他們執行一些複雜的數據轉換，將不可分離的數據集轉換為可分離的數據集。

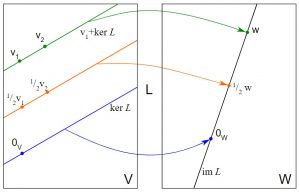
資源

SVM 內核有哪些不同類型？

線性內核

顧名思義，線性核用於線性可分的數據集。 它主要用於具有大量特徵的數據集，例如文本分類，其中所有字母都是新特徵。 線性核的語法是：

K(x, y) = 總和(x*y)

語法中的 x 和 y 是兩個向量。

使用線性核訓練 SVM 比使用任何其他核訓練更快，因為它只需要優化 C 正則化參數，而不需要優化 gamma 參數。

多項式核

多項式核是線性核的更通用形式，可用於轉換非線性數據集。 多項式核的公式如下：

K(x, y) = (xT*y + c)d

這裡 x 和 y 是兩個向量，c 是允許在高維和低維項之間進行權衡的常數，d 是內核的階數。 開發人員應該在算法中手動決定內核的順序。

徑向基函數內核

徑向基函數核，也稱為高斯核，是SVM 算法中廣泛使用的核，用於解決分類問題。 它有可能將輸入數據映射到不確定的高維空間。 徑向基函數核在數學上可以表示為：

K(x, y) = exp(-gamma*sum(x – y2))

這裡，x 和 y 是兩個向量，gamma 是一個從 0 到 1 的調整參數。 Gamma 是在學習算法中手動預定義的。

線性、多項式和徑向基函數的不同之處在於它們用於製定超平面創建決策和準確性的數學方法。 線性和多項式內核在訓練中消耗的時間較少，但提供的準確性較低。 另一方面，徑向基函數核在訓練中需要更多時間，但在結果方面提供更高的準確性。

現在出現的問題是如何選擇用於數據集的內核。 您的決定應僅取決於數據集的複雜性和所需結果的準確性。 當然，每個人都想要高精度的結果，但這也取決於您開發解決方案所需的時間以及您可以花多少錢。 此外，徑向基函數內核通常提供更高的精度，但在某些情況下，線性和多項式內核的性能同樣出色。

例如，對於線性可分數據，線性核的性能與徑向基核一樣好，同時消耗更少的訓練時間。 所以如果你的數據集是線性可分的，你應該選擇一個線性核。 對於非線性數據，您應該根據您擁有的時間和費用選擇多項式或徑向基函數。

內核使用的調優參數是什麼？

C 正則化

C 正則化參數接受您提供的值，以允許在每個訓練數據集中出現一定程度的錯誤分類。 較高的 C 正則化值會導緻小邊距超平面，並且不允許出現太多錯誤分類。 另一方面，較低的值會導致高利潤和更大的錯誤分類。

伽瑪

gamma 參數定義了將影響超平面定位的支持向量的範圍。 高 gamma 值僅考慮附近的數據點，低值考慮較遠的點。

如何在 Python 中實現支持向量機算法？

資源

既然我們對什麼是SVM 算法以及它是如何工作的有了基本的了解，那麼讓我們深入研究一些更複雜的東西。 現在我們將看看在 Python中實現和運行SVM 算法的一般步驟。 我們將使用 Python 的 Scikit-Learn 庫來學習如何實現SVM 算法。

首先，我們必須導入運行SVM 算法所需的所有必要庫，例如 Pandas 和 NumPy。 一旦我們有了所有的庫，我們就必須導入訓練數據集。 接下來，我們必須分析我們的數據集。 有多種方法可以分析數據集。

例如，我們可以檢查數據的維度，將其分為響應變量和解釋變量，並設置 KPI 來分析我們的數據集。 完成數據分析後，我們必須對數據集進行預處理。 我們應該檢查數據集中不相關、不完整和不正確的數據。

現在是訓練部分。 我們必須用相關的內核編碼和訓練我們的算法。 Scikit-Learn 包含 SVM 庫，您可以在其中找到一些用於訓練算法的內置類。 SVM 庫包含一個 SVC 類，該類接受您要用於訓練算法的內核類型的值。

然後調用訓練算法的 SVC 類的 fit 方法，將其作為參數插入 fit 方法。 然後，您必須使用 SVC 類的 predict 方法對算法進行預測。 完成預測步驟後，您必須調用度量庫的分類報告和混淆矩陣來評估您的算法並查看結果。

支持向量機算法有哪些應用？

SVM 算法在各種回歸和分類挑戰中都有應用。 SVM 算法的一些關鍵應用包括：

• 文本和超文本分類
• 圖像分類
• 合成孔徑雷達 (SAR) 等衛星數據的分類
• 對蛋白質等生物物質進行分類
• 手寫文本中的字符識別

為什麼要使用支持向量機算法？

SVM 算法提供各種好處，例如：

• 有效分離非線性數據
• 在低維和高維空間中都非常準確
• 不受過度擬合問題的影響，因為支持向量僅影響超平面的位置。

查看：您需要了解的 6 種神經網絡激活函數

加起來

我們已經詳細了解了本文中的支持向量機算法。 我們了解了SVM 算法、它的工作原理、它的類型、應用程序、優點和 Python 中的實現。 本文將為您提供有關SVM 算法的基本概念並回答您的一些問題。

但它也會帶來一些其他問題，例如SVM 算法如何知道正確的超平面是什麼，Python 中還有哪些其他可用的庫，以及在哪裡可以找到訓練數據集？ 如果您有興趣了解有關機器學習的更多信息，請查看 IIIT-B 和 upGrad 的機器學習和人工智能 PG 文憑，該文憑專為工作專業人士設計，提供 450 多個小時的嚴格培訓、30 多個案例研究和作業、IIIT- B 校友身份、5 個以上實用的實踐頂點項目和頂級公司的工作協助。