机器学习中的支持向量机算法

关于支持向量机算法你需要知道的一切

大多数初学者，当谈到机器学习时，自然会从回归和分类算法开始。 这些算法简单易懂。 但是，必须超越这两种机器学习算法才能更好地掌握机器学习的概念。

机器学习还有很多东西要学，可能不像回归和分类那么简单，但可以帮助我们解决各种复杂的问题。 让我们向您介绍一种这样的算法，即支持向量机算法。 支持向量机算法或SVM 算法通常被称为一种这样的机器学习算法，它可以为回归和分类问题提供效率和准确性。

如果您梦想在机器学习领域从事职业，那么支持向量机应该是您学习武器库的一部分。 在upGrad ，我们相信为我们的学生提供最好的机器学习算法，以开始他们的职业生涯。 以下是我们认为可以帮助您从机器学习中的SVM 算法开始的内容。

什么是支持向量机算法？

SVM 是一种监督学习算法，在 2020 年变得非常流行，并且在未来还会继续流行。 SVM 的历史可以追溯到 1990 年； 它来自 Vapnik 的统计学习理论。 SVM 可用于回归和分类挑战； 但是，它主要用于解决分类挑战。

SVM 是一种判别分类器，它在 N 维空间中创建超平面，其中 n 是数据集中的特征数，以帮助区分未来的数据输入。 听起来很混乱，别担心，我们会用简单的外行术语来理解它。

支持向量机算法如何工作？

在深入研究 SVM 的工作原理之前，让我们先了解一些关键术语。

超平面

超平面，有时也称为决策边界或决策平面，是帮助对数据点进行分类的边界。 新数据点所在的超平面一侧可以被隔离或归因于不同的类别。 超平面的维度取决于归属于数据集的特征数量。 如果数据集有 2 个特征，那么超平面可以是一条简单的线。 当一个数据集有 3 个特征时，超平面就是一个二维平面。

支持向量

支持向量是最接近超平面并影响其位置的数据点。 由于这些向量影响超平面定位，因此它们被称为支持向量，因此称为支持向量机算法。

利润

简单地说，margin 就是超平面和支持向量之间的差距。 SVM 总是选择最大化边距的超平面。 边际越大，结果的准确性就越高。 SVM 算法中使用两种类型的边距，硬边距和软边距。

当训练数据集线性可分时，SVM可以简单地选择两条边际距离最大化的平行线； 这称为硬边距。 当训练数据集不是完全线性分离时，SVM 允许一些边距违规。 它允许一些数据点停留在超平面的错误一侧或边缘和超平面之间，从而不影响准确性； 这称为软边距。

给定数据集可能有许多可能的超平面。 VSM 的目标是选择最大的边距来将新数据点分类到不同的类别中。 添加新数据点时，SVM 会确定数据点落在超平面的哪一侧。 基于新数据点所在的超平面的一侧，SVM 然后将其分类为不同的类别。

阅读：机器学习的线性代数：关键概念，为什么要在机器学习之前学习

支持向量机的类型有哪些？

基于训练数据集， SVM算法s可以有两种类型：

线性支持向量机

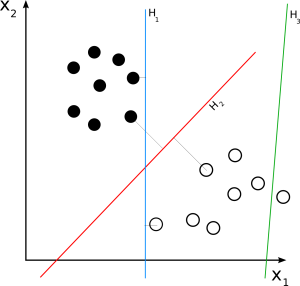
资源

线性 SVM 用于线性可分数据集。 一个简单的真实示例可以帮助我们理解线性 SVM 的工作原理。 考虑一个具有单一特征的数据集，即人的体重。 数据点可以被分为两类，肥胖或不肥胖。 为了将数据点分为这两类，SVM 可以在最近的支持向量的帮助下创建一个最大边距超平面。 现在，每当添加一个新数据点时，SVM 都会检测超平面的一侧，它落在哪里，并将此人分类为肥胖与否。

非线性支持向量机

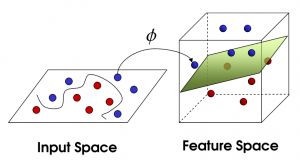
资源

随着特征数量的增加，线性分离数据集变得具有挑战性。 这就是使用非线性 SVM 的地方。 当数据集不是线性可分的时，我们不能画一条直线来分隔数据点。 因此，为了分离这些数据点，SVM 添加了另一个维度。 新维度 z 可以计算为 z = x2 + Y2。 这种计算将有助于以线性形式分离数据集的特征，然后 SVM 可以创建超平面来对数据点进行分类。

当通过添加新维度将数据点转换为高维空间时，它可以很容易地与超平面分离。 这是在所谓的内核技巧的帮助下完成的。 借助内核技巧， SVM 算法可以将不可分离的数据转换为可分离的数据。

什么是内核？

内核是一个函数，它接受低维输入并将它们转换为高维空间。 它也被称为有助于提高 SVM 输出准确性的调整参数。 他们执行一些复杂的数据转换，将不可分离的数据集转换为可分离的数据集。

资源

SVM 内核有哪些不同类型？

线性内核

顾名思义，线性核用于线性可分的数据集。 它主要用于具有大量特征的数据集，例如文本分类，其中所有字母都是新特征。 线性核的语法是：

K(x, y) = 总和(x*y)

语法中的 x 和 y 是两个向量。

使用线性核训练 SVM 比使用任何其他核训练更快，因为它只需要优化 C 正则化参数，而不需要优化 gamma 参数。

多项式核

多项式核是线性核的更通用形式，可用于转换非线性数据集。 多项式核的公式如下：

K(x, y) = (xT*y + c)d

这里 x 和 y 是两个向量，c 是允许在高维和低维项之间进行权衡的常数，d 是内核的阶数。 开发人员应该在算法中手动决定内核的顺序。

径向基函数内核

径向基函数核，也称为高斯核，是SVM 算法中广泛使用的核，用于解决分类问题。 它有可能将输入数据映射到不确定的高维空间。 径向基函数核在数学上可以表示为：

K(x, y) = exp(-gamma*sum(x – y2))

这里，x 和 y 是两个向量，gamma 是一个从 0 到 1 的调整参数。 Gamma 是在学习算法中手动预定义的。

线性、多项式和径向基函数的不同之处在于它们用于制定超平面创建决策和准确性的数学方法。 线性和多项式内核在训练中消耗的时间较少，但提供的准确性较低。 另一方面，径向基函数核在训练中需要更多时间，但在结果方面提供更高的准确性。

现在出现的问题是如何选择用于数据集的内核。 您的决定应仅取决于数据集的复杂性和所需结果的准确性。 当然，每个人都想要高精度的结果，但这也取决于您开发解决方案所需的时间以及您可以花多少钱。 此外，径向基函数内核通常提供更高的精度，但在某些情况下，线性和多项式内核的性能同样出色。

例如，对于线性可分数据，线性核的性能与径向基核一样好，同时消耗更少的训练时间。 所以如果你的数据集是线性可分的，你应该选择一个线性核。 对于非线性数据，您应该根据您拥有的时间和费用选择多项式或径向基函数。

内核使用的调优参数是什么？

C 正则化

C 正则化参数接受您提供的值，以允许在每个训练数据集中出现一定程度的错误分类。 较高的 C 正则化值会导致小边距超平面，并且不允许出现太多错误分类。 另一方面，较低的值会导致高利润和更大的错误分类。

伽玛

gamma 参数定义了将影响超平面定位的支持向量的范围。 高 gamma 值仅考虑附近的数据点，低值考虑较远的点。

如何在 Python 中实现支持向量机算法？

资源

既然我们对什么是SVM 算法以及它是如何工作的有了基本的了解，那么让我们深入研究一些更复杂的东西。 现在我们将看看在 Python中实现和运行SVM 算法的一般步骤。 我们将使用 Python 的 Scikit-Learn 库来学习如何实现SVM 算法。

首先，我们必须导入运行SVM 算法所需的所有必要库，例如 Pandas 和 NumPy。 一旦我们有了所有的库，我们就必须导入训练数据集。 接下来，我们必须分析我们的数据集。 有多种方法可以分析数据集。

例如，我们可以检查数据的维度，将其分为响应变量和解释变量，并设置 KPI 来分析我们的数据集。 完成数据分析后，我们必须对数据集进行预处理。 我们应该检查数据集中不相关、不完整和不正确的数据。

现在是训练部分。 我们必须用相关的内核编码和​​训练我们的算法。 Scikit-Learn 包含 SVM 库，您可以在其中找到一些用于训练算法的内置类。 SVM 库包含一个 SVC 类，该类接受您要用于训练算法的内核类型的值。

然后调用训练算法的 SVC 类的 fit 方法，将其作为参数插入 fit 方法。 然后，您必须使用 SVC 类的 predict 方法对算法进行预测。 完成预测步骤后，您必须调用度量库的分类报告和混淆矩阵来评估您的算法并查看结果。

支持向量机算法有哪些应用？

SVM 算法在各种回归和分类挑战中都有应用。 SVM 算法的一些关键应用包括：

• 文本和超文本分类
• 图像分类
• 合成孔径雷达 (SAR) 等卫星数据的分类
• 对蛋白质等生物物质进行分类
• 手写文本中的字符识别

为什么要使用支持向量机算法？

SVM 算法提供各种好处，例如：

• 有效分离非线性数据
• 在低维和高维空间中都非常准确
• 不受过度拟合问题的影响，因为支持向量仅影响超平面的位置。

查看：您需要了解的 6 种神经网络激活函数

加起来

我们已经详细了解了本文中的支持向量机算法。 我们了解了SVM 算法、它的工作原理、它的类型、应用程序、优点和 Python 中的实现。 本文将为您提供有关SVM 算法的基本概念并回答您的一些问题。

但它也会带来一些其他问题，例如SVM 算法如何知道正确的超平面是什么，Python 中还有哪些其他可用的库，以及在哪里可以找到训练数据集？ 如果您有兴趣了解有关机器学习的更多信息，请查看 IIIT-B 和 upGrad 的机器学习和人工智能 PG 文凭，该文凭专为工作专业人士设计，提供 450 多个小时的严格培训、30 多个案例研究和作业、IIIT- B 校友身份、5 个以上实用的实践顶点项目和顶级公司的工作协助。