MCMC Yöntemleri: Metropolis-Hastings ve Bayes Çıkarımı
Yayınlanan: 2022-03-11Temel tanımı aradan çıkaralım: Markov Zinciri Monte Carlo (MCMC) yöntemleri, bir dağılımdan örnekleri hesaplayamasak bile hesaplamamıza izin verir.
Ne anlama geliyor? Geri çekilelim ve Monte Carlo Örneklemesi hakkında konuşalım.
Monte Carlo Örneklemesi
Monte Carlo yöntemleri nelerdir?
"Monte Carlo yöntemleri veya Monte Carlo deneyleri, sayısal sonuçlar elde etmek için tekrarlanan rastgele örneklemeye dayanan geniş bir hesaplama algoritmaları sınıfıdır." (Vikipedi)
Bunu parçalayalım.
Örnek 1: Alan Tahmini
Aşağıda sunulan şekil gibi düzensiz bir şekle sahip olduğunuzu hayal edin:
Ve bu şeklin çevrelediği alanı belirleme göreviniz var. Kullanabileceğiniz yöntemlerden biri, şekilde küçük kareler yapmak, kareleri saymaktır ve bu size alanın oldukça doğru bir tahminini verecektir. Ancak bu zor ve zaman alıcıdır.
Kurtarmak için Monte Carlo örneklemesi!
İlk olarak, şeklin etrafına bilinen bir alana sahip büyük bir kare çiziyoruz, örneğin 50 cm2. Şimdi bu kareyi “asıyoruz” ve şekle rastgele dart atmaya başlıyoruz.
Ardından, dikdörtgendeki toplam dart sayısını ve ilgilendiğimiz şekildeki dart sayısını sayarız. Kullanılan toplam “dart” sayısının 100 olduğunu ve 22 tanesinin şeklin içinde kaldığını varsayalım. Şimdi alan basit formülle hesaplanabilir:
şekil alanı = kare alanı *(şekildeki dart sayısı) / (karedeki dart sayısı)
Yani, bizim durumumuzda, bu aşağı geliyor:
şekil alanı = 50 * 22/100 = 11 cm2
"Dart" sayısını 10 ile çarparsak, bu yaklaşım gerçek cevaba çok yakın olur:
şekil alanı = 50 * 280/1000 = 14 cm2
Monte Carlo örneklemesini kullanarak yukarıda verilen gibi karmaşık görevleri bu şekilde yıkıyoruz.
Büyük Sayılar Yasası
Alan yaklaşımı, ne kadar çok dart atarsak o kadar yakındı ve bunun nedeni Büyük Sayılar Yasası:
"Büyük sayılar yasası, aynı deneyi çok sayıda gerçekleştirmenin sonucunu tanımlayan bir teoremdir. Yasaya göre, çok sayıda denemeden elde edilen sonuçların ortalaması beklenen değere yakın olmalı ve daha fazla deneme yapıldıkça daha yakın olma eğiliminde olacaktır.”
Bu bizi bir sonraki örneğimize, ünlü Monty Hall problemine getiriyor.
Örnek 2: Monty Hall Problemi
Monty Hall problemi çok ünlü bir zeka oyunudur:
“Üç kapı var, birinin arkasında araba, diğerlerinin arkasında keçi var. Bir kapı seçiyorsunuz, ev sahibi farklı bir kapı açıyor ve size arkasında bir keçi olduğunu gösteriyor. Daha sonra kararınızı değiştirmek isteyip istemediğinizi sorar. Öyle mi? Niye ya? Neden?"
Aklınıza gelen ilk şey, değişseniz de, değiştirmeseniz de kazanma şansınızın eşit olduğudur, ancak bu doğru değildir. Aynı şeyi göstermek için basit bir akış şeması yapalım.
Arabanın 3 numaralı kapının arkasında olduğunu varsayarsak:
Dolayısıyla, değiştirirseniz ⅔ kez kazanırsınız ve değiştirmezseniz yalnızca ⅓ kez kazanırsınız.
Bunu örnekleme kullanarak çözelim.
wins = [] for i in range(int(10e6)): car_door = assign_car_door() choice = random.randint(0, 2) opened_door = assign_door_to_open(car_door) did_he_win = win_or_lose(choice, car_door, opened_door, switch = False) wins.append(did_he_win) print(sum(wins)/len(wins)) assign_car_door() işlevi, arkasında bir araba bulunan bir kapı 0, 1 veya 2'yi seçen rastgele bir sayı üretecidir. assign_door_to_open kullanımı, arkasında keçi olan ve sizin seçtiğiniz kapı olmayan bir kapıyı seçer ve sunucu onu açar. win_or_lose , arabayı kazanıp kazanmadığınızı belirten doğru veya yanlış döndürür, kapıyı değiştirip değiştirmediğinizi söyleyen bir bool "switch" alır.
Bu simülasyonu 10 milyon kez çalıştıralım:
- Geçiş yapmazsanız kazanma olasılığı: 0.334134
- Geçiş yaparsanız kazanma olasılığı: 0.667255
Bu, akış şemasının bize verdiği cevaplara çok yakın.
Aslında, bu simülasyonu ne kadar çok çalıştırırsak, cevap gerçek değere o kadar yaklaşır, dolayısıyla büyük sayılar yasasını doğrular:
Aynı şey bu tablodan da görülebilir:
| Simülasyonlar çalıştırılır | Değiştirirseniz kazanma olasılığı | Geçiş yapmazsanız kazanma olasılığı |
| 10 | 0,6 | 0,2 |
| 10^2 | 0.63 | 0.33 |
| 10^3 | 0.661 | 0.333 |
| 10^4 | 0.6683 | 0.3236 |
| 10^5 | 0.66762 | 0.33171 |
| 10^6 | 0.667255 | 0.334134 |
| 10^7 | 0.6668756 | 0.3332821 |
Bayesyen Düşünme Yolu
"İstatistiğin daha klasik versiyonu olarak bilinen sık sık, olasılığın olayların uzun vadeli sıklığı (dolayısıyla bahşedilen başlık) olduğunu varsayar."
“Bayes istatistikleri, olasılığın bir olaya olan inancın derecesini ifade ettiği Bayesci olasılık yorumuna dayanan istatistik alanında bir teoridir. İnanç derecesi, önceki deneylerin sonuçları gibi olayla ilgili ön bilgilere veya olayla ilgili kişisel inançlara dayanabilir. - Hackerlar için Olasılıksal Programlama ve Bayes Yöntemlerinden
Ne anlama geliyor?
Sık sık düşünme tarzında, uzun vadede olasılıklara bakarız. Sıkça kullanan biri %0,001'lik bir araba kazası olasılığının olduğunu söylediğinde, bu, sonsuz araba yolculuklarını düşünürsek, bunların %0,001'inin kazayla sonuçlanacağı anlamına gelir.
Bir Bayes zihniyeti farklıdır, çünkü bir öncekiyle, bir inançla başlarız. 0 inancından bahsedersek, olayın asla olmayacağına olan inancınız; tersine, 1 inancı, bunun olacağından emin olduğunuz anlamına gelir.
Ardından, verileri gözlemlemeye başladığımızda, verileri dikkate almak için bu inancı güncelliyoruz. Bunu nasıl yapabiliriz? Bayes teoremini kullanarak.
Bayes teoremi
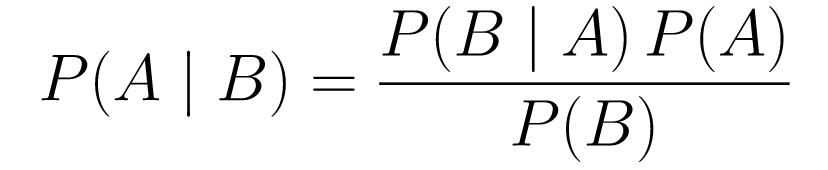 ....(1)
....(1)Hadi parçalayalım.
-
P(A | B)bize, verilen B olayı için A olayının olasılığını verir. Bu sonsaldır, B gözlemlediğimiz verilerdir, yani esasen gözlemlediğimiz verileri göz önünde bulundurarak bir olayın olma olasılığının ne olduğunu söylüyoruz. -
P(A)önceliklidir, A olayının olacağına dair inancımızdır. -
P(B | A)olasılıktır, A'nın doğru olduğu verilen verileri gözlemleme olasılığımız nedir.
Bir örneğe bakalım, kanser tarama testi.
Kanser Olasılığı
Diyelim ki bir hasta mamografi çektirmeye gitti ve mamogram pozitif çıktı. Hastanın gerçekten kanser olma olasılığı nedir?
Olasılıkları tanımlayalım:
- Kadınların %1'inde meme kanseri vardır.
- Mamogramlar, kanserin gerçekten var olduğu zamanın %80'inde kanseri tespit eder.
- Mamogramların %9,6'sı aslında kanser olmadığınızı söylerken yanlış bir şekilde kanser olduğunuzu bildiriyor.
Yani, eğer bir mamogram pozitif çıktıysa, yani kanser olma ihtimalinizin %80 olduğunu söylerseniz, bu yanlış olur. Kanser olmanın nadir görülen bir olay olduğunu, yani kadınların sadece %1'inde meme kanseri olduğunu dikkate almazsınız. Bunu öncelikli olarak almamız gerekiyor ve işte burada Bayes teoremi devreye giriyor:
P(C+ | T+) =(P(T+|C+)*P(C+))/P(T+)
-
P(C+ | T+): Bu, testin pozitif olduğu göz önüne alındığında, kanserin orada olma olasılığı, ilgilendiğimiz şey bu. -
P(T+ | C+): Bu, kanser olduğu için testin pozitif olma olasılığıdır, yukarıda tartışıldığı gibi bu, %80 = 0.8'e eşittir. -
P(C+): Bu, önceki olasılıktır, bir bireyin kansere sahip olma olasılığı, %1 = 0.01'e eşittir. -
P(T+): Bu, ne olursa olsun testin pozitif olma olasılığıdır, yani iki bileşeni vardır: P(T+) = P(T+|C-) P(C-)+P(T+|C+) P (C+) -
P(T+ | C-): Bu, testin pozitif çıkması ancak kanser olmaması olasılığıdır, bu 0.096 ile verilir. -
P(C-): Bu, kanser olma olasılığı %1 olduğu için kanser olmama olasılığıdır, bu %99 = 0.99'a eşittir. -
P(T+ | C+): Bu, kanseriniz varsa testin pozitif çıkma olasılığıdır, bu %80 = 0,8'e eşittir. -
P(C+): Bu, %1 = 0.01 olan kanser olma olasılığıdır.
Tüm bunları orijinal formüle takarak:
Yani, mamogramın pozitif çıktığı düşünülürse, hastanın kanser olma olasılığı %7,76'dır. İlk başta garip gelebilir ama mantıklı. Test, zamanın %9,6'sında (oldukça yüksek) yanlış pozitif verir, bu nedenle belirli bir popülasyonda birçok yanlış pozitif olacaktır. Nadir bir hastalık için, pozitif test sonuçlarının çoğu yanlış olacaktır.
Şimdi Monty Hall problemini tekrar gözden geçirelim ve Bayes teoremini kullanarak çözelim.
Monty Hall Problemi
Öncelik şu şekilde tanımlanabilir:
- Başlangıçta A kapısını seçtiğinizi varsayalım.
- P(H) = ⅓, ⅓. ⅓ Her üç kapı için, yani kapı açılmadan ve keçi ortaya çıkmadan önce, arabanın herhangi birinin arkasında olma olasılığı eşitti.
Olasılık şu şekilde tanımlanabilir:

-
P(D|H), burada D olayı Monty'nin B kapısını seçmesi ve arkasında araba olmamasıdır. - Araba A kapısının arkasındaysa
P(D|H)= 1/2 - çünkü %50 B kapısını seçme şansı ve %50 C kapısını seçme şansı var. - Araba B kapısının arkasındaysa
P(D|H)= 0, çünkü araba arkasındaysa B kapısını seçme olasılığı %0. -
P(D|H)= 1 eğer araba C'nin arkasındaysa ve siz A'yı seçerseniz, onun B kapısını seçme olasılığı %100'dür.
Biz P(H|D) ile ilgileniyoruz, ki bu bize diğer kapılardan birinin arkasındaki keçiyi gösterdiğine göre arabanın bir kapının arkasında olma olasılığıdır.
Arkadan, P(H|D) görülebilir, A'dan C kapısına geçmenin kazanma olasılığını artıracağı.
Metropolis-Hastings
Şimdi, şimdiye kadar ele aldığımız her şeyi birleştirelim ve Metropolis-Hastings'in nasıl çalıştığını anlamaya çalışalım.
Metropolis-Hastings, doğrudan örneklemenin zor olduğu karmaşık bir dağılımın sonsal dağılımını elde etmek için Bayes teoremini kullanır.
Nasıl? Esasen, bir uzaydan rastgele farklı örnekler seçer ve yeni örneğin son örnekten daha sondan olma olasılığının daha yüksek olup olmadığını kontrol eder, çünkü olasılıkların oranına baktığımız için denklem (1)'deki P(B) alır. iptal edildi:
P(kabul) = ( P(yeniÖrnek) * Yeni örnek olasılığı) / (P(eskiÖrnek) * Eski örnek olasılığı)
Her yeni örneğin “olasılığına” f fonksiyonu tarafından karar verilir. Bu nedenle f , örneklemek istediğimiz posterior ile orantılı olmalıdır.
θ′'nin kabul edilip edilmeyeceğine karar vermek için, önerilen her yeni θ' için aşağıdaki oran hesaplanmalıdır:
θ eski örnek olduğunda, P(D| θ) , θ örneğinin olasılığıdır.
Bunu daha iyi anlamak için bir örnek kullanalım. Diyelim ki verileriniz var ama buna uyan normal dağılımı bulmak istiyorsunuz, yani:
X ~ N(ortalama, standart)
Şimdi hem ortalama hem de standart için öncelikleri tanımlamamız gerekiyor. Basit olması için, her ikisinin de ortalama 1 ve std 2 ile normal bir dağılım izlediğini varsayacağız:
Ortalama ~ N(1, 2)
standart ~ N(1, 2)
Şimdi, biraz veri üretelim ve gerçek ortalamanın ve std'nin sırasıyla 0,5 ve 1,2 olduğunu varsayalım.
import numpy as np import matplotlib.pyplot as plt import scipy.stats as st meanX = 1.5 stdX = 1.2 X = np.random.normal(meanX, stdX, size = 1000) _ = plt.hist(X, bins = 50)PyMC3
Önce verileri modellemek ve ortalama ve std için sonsal dağılımı bulmak için PyMC3 adlı bir kitaplık kullanalım.
import pymc3 as pm with pm.Model() as model: mean = pm.Normal("mean", mu = 1, sigma = 2) std = pm.Normal("std", mu = 1, sigma = 2) x = pm.Normal("X", mu = mean, sigma = std, observed = X) step = pm.Metropolis() trace = pm.sample(5000, step = step)Kodun üzerinden geçelim.
İlk olarak, ortalama ve std için önceliği tanımlarız, yani ortalama 1 ve std 2 olan bir normali tanımlarız.
x = pm.Normal(“X”, mu = ortalama, sigma = std, gözlenen = X)
Bu satırda ilgilendiğimiz değişkeni tanımlarız; daha önce tanımladığımız ortalama ve std'yi alır, daha önce hesapladığımız gözlenen değerleri de alır.
Sonuçlara bakalım:
_ = plt.hist(trace['std'], bins = 50, label = "std") _ = plt.hist(trace['mean'], bins = 50, label = "mean") _ = plt.legend()Standart 1.2 civarında ortalanmış ve ortalama 1.55'te - oldukça yakın!
Şimdi Metropolis-Hastings'i anlamak için sıfırdan yapalım.
Sıfırdan
Teklif Oluşturma
Öncelikle Metropolis-Hastings'in ne yaptığını anlayalım. Bu makalenin başlarında, “Metropolis-Hastings bir uzaydan rastgele farklı örnekler seçer” demiştik ama hangi örneği seçeceğini nasıl biliyor?
Bunu teklif dağıtımını kullanarak yapar. Şu anda kabul edilen örnek merkezli normal bir dağılımdır ve STD'si 0,5'tir. 0,5 bir hiper parametre olduğunda, ince ayar yapabiliriz; teklifin STD'si ne kadar fazlaysa, şu anda kabul edilen örnekten o kadar uzakta arama yapacaktır. Bunu kodlayalım.
Dağılımın ortalamasını ve std'sini bulmamız gerektiğinden, bu fonksiyon şu anda kabul edilen ortalamayı ve şu anda kabul edilen std'yi alacak ve her ikisi için teklifleri döndürecektir.
def get_proposal(mean_current, std_current, proposal_width = 0.5): return np.random.normal(mean_current, proposal_width), \ np.random.normal(std_current, proposal_width)Bir Teklifi Kabul Etme/Reddetme
Şimdi teklifi kabul eden veya reddeden mantığı kodlayalım. İki bölümü vardır: önceki ve olasılık .
İlk olarak, teklifin öncekinden gelme olasılığını hesaplayalım:
def prior(mean, std, prior_mean, prior_std): return st.norm(prior_mean[0], prior_mean[1]).pdf(mean)* \ st.norm(prior_std[0], prior_std[1]).pdf(std)Sadece ortalamayı ve std'yi alır ve bu ortalama ve std'nin tanımladığımız önceki dağılımdan gelme olasılığını hesaplar.
Olasılığı hesaplarken, gördüğümüz verilerin önerilen dağılımdan gelme olasılığını hesaplıyoruz.
def likelihood(mean, std, data): return np.prod(st.norm(mean, std).pdf(X))Bu nedenle, her veri noktası için, o veri noktasının önerilen dağılımdan gelme olasılığını çarpıyoruz.
Şimdi, bu fonksiyonları mevcut ortalama ve std için ve önerilen ortalama ve std için çağırmamız gerekiyor.
prior_current = prior(mean_current, std_current, prior_mean, prior_std) likelihood_current = likelihood(mean_current, std_current, data) prior_proposal = prior(mean_proposal, std_proposal, prior_mean, prior_std) likelihood_proposal = likelihood(mean_proposal, std_proposal, data)Kodun tamamı:
def accept_proposal(mean_proposal, std_proposal, mean_current, \ std_current, prior_mean, prior_std, data): def prior(mean, std, prior_mean, prior_std): return st.norm(prior_mean[0], prior_mean[1]).pdf(mean)* \ st.norm(prior_std[0], prior_std[1]).pdf(std) def likelihood(mean, std, data): return np.prod(st.norm(mean, std).pdf(X)) prior_current = prior(mean_current, std_current, prior_mean, prior_std) likelihood_current = likelihood(mean_current, std_current, data) prior_proposal = prior(mean_proposal, std_proposal, prior_mean, prior_std) likelihood_proposal = likelihood(mean_proposal, std_proposal, data) return (prior_proposal * likelihood_proposal) / (prior_current * likelihood_current)Şimdi, her şeyi birbirine bağlayacak ve ihtiyacımız olan sonsal örnekleri oluşturacak son işlevi oluşturalım.
Posterior Oluşturma
Şimdi yukarıda yazdığımız fonksiyonları çağırıyoruz ve posterioru üretiyoruz!
def get_trace(data, samples = 5000): mean_prior = 1 std_prior = 2 mean_current = mean_prior std_current = std_prior trace = { "mean": [mean_current], "std": [std_current] } for i in tqdm(range(samples)): mean_proposal, std_proposal = get_proposal(mean_current, std_current) acceptance_prob = accept_proposal(mean_proposal, std_proposal, mean_current, \ std_current, [mean_prior, std_prior], \ [mean_prior, std_prior], data) if np.random.rand() < acceptance_prob: mean_current = mean_proposal std_current = std_proposal trace['mean'].append(mean_current) trace['std'].append(std_current) return traceİyileştirme Odası
Günlük senin arkadaşın!
a * b = antilog(log(a) + log(b)) ve a / b = antilog(log(a) - log(b)).
Bu bizim için faydalıdır çünkü çok küçük olasılıklarla uğraşacağız, çarpma işlemi sıfırla sonuçlanacak, bu yüzden log probunu eklemeyi tercih edeceğiz, problem çözüldü!
Böylece önceki kodumuz şu hale gelir:
def accept_proposal(mean_proposal, std_proposal, mean_current, \ std_current, prior_mean, prior_std, data): def prior(mean, std, prior_mean, prior_std): return st.norm(prior_mean[0], prior_mean[1]).logpdf(mean)+ \ st.norm(prior_std[0], prior_std[1]).logpdf(std) def likelihood(mean, std, data): return np.sum(st.norm(mean, std).logpdf(X)) prior_current = prior(mean_current, std_current, prior_mean, prior_std) likelihood_current = likelihood(mean_current, std_current, data) prior_proposal = prior(mean_proposal, std_proposal, prior_mean, prior_std) likelihood_proposal = likelihood(mean_proposal, std_proposal, data) return (prior_proposal + likelihood_proposal) - (prior_current + likelihood_current)Kabul olasılığı günlüğünü döndürdüğümüz için:
if np.random.rand() < acceptance_prob:
olur:
if math.log(np.random.rand()) < acceptance_prob:
Yeni kodu çalıştıralım ve sonuçları çizelim.
_ = plt.hist(trace['std'], bins = 50, label = "std") _ = plt.hist(trace['mean'], bins = 50, label = "mean") _ = plt.legend()Gördüğünüz gibi, standart 1.2'de ortalanmış ve ortalama 1.5'te. Yaptık!
İlerlemek
Şimdiye kadar umarım Metropolis-Hastings'in nasıl çalıştığını anlamışsınızdır ve onu nerede kullanabileceğinizi merak ediyor olabilirsiniz.
Bayesian Methods for Hackers , olasılıksal programlamayı açıklayan mükemmel bir kitap ve Bayes teoremi ve uygulamaları hakkında daha fazla bilgi edinmek istiyorsanız, Think Bayes , Allen B. Downey tarafından yazılmış harika bir kitap.
Okuduğunuz için teşekkür ederim ve umarım bu makale sizi Bayes istatistiklerinin muhteşem dünyasını keşfetmeye teşvik eder.
