MCMC法:メトロポリス-ヘイスティングスとベイズ推定
公開: 2022-03-11基本的な定義を邪魔にならないようにしましょう。マルコフ連鎖モンテカルロ(MCMC)法では、分布を計算できなくても、分布からサンプルを計算できます。
これは何を意味するのでしょうか? バックアップして、モンテカルロサンプリングについて話しましょう。
モンテカルロサンプリング
モンテカルロ法とは何ですか?
「モンテカルロ法、またはモンテカルロ実験は、数値結果を得るために繰り返しランダムサンプリングに依存する幅広いクラスの計算アルゴリズムです。」 (ウィキペディア)
それを分解しましょう。
例1:面積の見積もり
以下に示すような不規則な形をしていると想像してみてください。
そして、あなたはこの形で囲まれた領域を決定する任務を負っています。 使用できる方法の1つは、形状に小さな正方形を作成し、その正方形を数えることです。これにより、面積をかなり正確に近似できます。 ただし、それは困難で時間がかかります。
モンテカルロサンプリングで救助!
まず、形状の周囲に既知の領域の大きな正方形、たとえば50cm2を描画します。 次に、この正方形を「吊るして」、その形状にランダムにダーツを投げ始めます。
次に、長方形のダーツの総数と、関心のある形状のダーツの数を数えます。使用された「ダーツ」の総数が100で、そのうちの22が形状内に収まったと仮定します。 これで、面積は次の簡単な式で計算できます。
形状の面積=正方形の面積*(形状のダーツの数)/(正方形のダーツの数)
したがって、私たちの場合、これは次のようになります。
形状の面積=50* 22/100 = 11 cm2
「ダーツ」の数に10を掛けると、この近似は実際の答えに非常に近くなります。
形状の面積=50* 280/1000 = 14 cm2
これは、モンテカルロサンプリングを使用して、上記のような複雑なタスクを分解する方法です。
大数の法則
投げるダーツが多いほど、面積の近似値は近くなりました。これは、大数の法則によるものです。
「大数の法則は、同じ実験を何度も実行した結果を表す定理です。 法律によれば、多数の試行から得られた結果の平均は期待値に近いはずであり、より多くの試行が実行されるにつれて近づく傾向があります。」
これにより、次の例である有名なモンティホール問題に移ります。
例2:モンティホール問題
モンティホール問題は非常に有名な頭の体操です。
「ドアは3つあり、1つは後ろに車があり、他のドアは後ろに山羊がいます。 あなたはドアを選び、ホストは別のドアを開け、その後ろに山羊がいることを示します。 それから彼はあなたがあなたの決定を変えたいかどうかあなたに尋ねます。 あなたは? なんで? なぜだめですか?"
最初に頭に浮かぶのは、切り替えるかどうかにかかわらず、勝つ可能性は同じであるということですが、それは真実ではありません。 同じことを示す簡単なフローチャートを作成しましょう。
車がドアの後ろにあると仮定します3:
したがって、切り替えた場合は2/3回勝ち、切り替えない場合は1/3回しか勝ちません。
サンプリングを使ってこれを解決しましょう。
wins = [] for i in range(int(10e6)): car_door = assign_car_door() choice = random.randint(0, 2) opened_door = assign_door_to_open(car_door) did_he_win = win_or_lose(choice, car_door, opened_door, switch = False) wins.append(did_he_win) print(sum(wins)/len(wins)) assign_car_door()関数は、ドア0、1、または2を選択する単なる乱数ジェネレーターであり、その後ろに車があります。 assign_door_to_openを使用すると、背後に山羊がいて、選択したドアではないドアが選択され、ホストがドアを開きます。 win_or_loseはtrueまたはfalseを返し、車に勝ったかどうかを示します。ドアを切り替えたかどうかを示すブール値の「スイッチ」が必要です。
このシミュレーションを1000万回実行してみましょう。
- 切り替えない場合の当選確率:0.334134
- 切り替えた場合の当選確率:0.667255
これは、フローチャートが示した答えに非常に近いものです。
実際、このシミュレーションを実行すればするほど、答えは真の値に近づき、大数の法則が検証されます。
この表からも同じことがわかります。
| シミュレーションの実行 | 切り替えた場合の当選確率 | 切り替えない場合の当選確率 |
| 10 | 0.6 0.6 | 0.2 |
| 10 ^ 2 | 0.63 | 0.33 |
| 10 ^ 3 | 0.661 | 0.333 |
| 10 ^ 4 | 0.6683 | 0.3236 |
| 10 ^ 5 | 0.66762 | 0.33171 |
| 10 ^ 6 | 0.667255 | 0.334134 |
| 10 ^ 7 | 0.6668756 | 0.3332821 |
ベイジアンの考え方
「統計のより古典的なバージョンとして知られている頻度主義者は、確率がイベントの長期的な頻度であると想定しています(したがって、授与されたタイトル)。」
「ベイズ統計は、確率のベイズ解釈に基づく統計の分野における理論であり、確率はイベントに対するある程度の信念を表します。 信念の程度は、以前の実験の結果など、イベントに関する事前の知識、またはイベントに関する個人的な信念に基づいている可能性があります。」 -ハッカーのための確率的プログラミングとベイズ法から
これは何を意味するのでしょうか?
頻度主義的考え方では、長期的には確率に注目します。 頻度主義者が自動車事故が発生する可能性が0.001%であると言った場合、それは、無限の自動車旅行を考慮すると、それらの0.001%が交通事故で終わることを意味します。
ベイジアンの考え方は異なります。これは、事前の信念から始めるためです。 私たちが0の信念について話す場合、それはあなたの信念がイベントが決して起こらないということを意味します。 逆に、1の信念は、それが起こると確信していることを意味します。
次に、データの観察を開始したら、データを考慮に入れるようにこの信念を更新します。 これをどのように行うのですか? ベイズの定理を使用する。
ベイズの定理
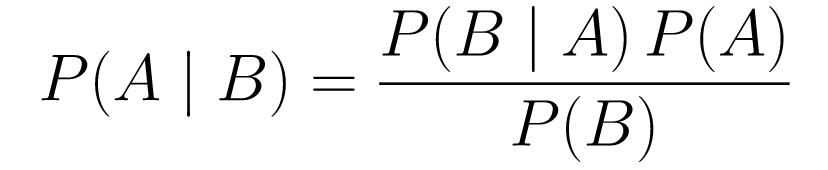 ....(1)
....(1)分解してみましょう。
-
P(A | B)は、イベントBが与えられた場合のイベントAの確率を示します。これは事後確率であり、Bは観測されたデータです。したがって、観測されたデータを考慮して、イベントが発生する確率は基本的に何であるかを示しています。 -
P(A)は事前のものであり、イベントAが発生するという私たちの信念です。 -
P(B | A)は尤度であり、Aが真であると仮定してデータを観測する確率はどのくらいですか。
例として、がん検診を見てみましょう。
がんの確率
患者がマンモグラムを完成させに行き、マンモグラムが陽性に戻ったとしましょう。 患者が実際に癌を患っている確率はどれくらいですか?
確率を定義しましょう:
- 女性の1%が乳がんを患っています。
- マンモグラムは、実際に存在する場合に80%の確率で癌を検出します。
- マンモグラムの9.6%は、実際には癌がないのに癌があると誤って報告しています。
したがって、マンモグラムが陽性に戻った場合、つまり癌にかかっている可能性が80%あると言えば、それは間違いです。 がんになることはまれな出来事である、つまり、女性の1%だけが乳がんにかかっていることを考慮に入れてはいけません。 これを前もってとる必要があり、ここでベイズの定理が作用します。
P(C + | T +)=(P(T + | C +)* P(C +))/ P(T +)
-
P(C+ | T+):これは、検査が陽性であったことを考えると、がんが存在する確率です。これが私たちが関心を持っていることです。 -
P(T+ | C+):これは、癌がある場合にテストが陽性である確率です。これは、上記のように、80%=0.8に等しくなります。 -
P(C+):これは事前確率であり、個人が癌を患う確率であり、1%=0.01に等しくなります。 -
P(T+):これは、何があってもテストが陽性である確率であるため、2つの要素があります。P(T +)= P(T + | C-) P(C-)+ P(T + | C +) P (C +) -
P(T+ | C-):これは、テストが陽性に戻ったが癌がない確率であり、これは0.096で与えられます。 -
P(C-):これは癌を持っている確率が1%であるため、癌を持っていない確率です。これは99%=0.99に等しくなります。 -
P(T+ | C+):これは、あなたが癌を持っているとすると、テストが陽性に戻った確率です。これは80%=0.8に等しくなります。 -
P(C+):これは癌になる確率であり、1%=0.01に相当します。
これらすべてを元の数式に接続します。
したがって、マンモグラムが陽性に戻ったことを考えると、患者が癌を患う可能性は7.76%です。 最初は奇妙に思えるかもしれませんが、それは理にかなっています。 このテストでは、9.6%の確率で誤検知が発生するため(かなり高い)、特定の母集団には多くの誤検知が発生します。 まれな病気の場合、陽性の検査結果のほとんどは間違っています。
ここで、モンティホール問題を再検討し、ベイズの定理を使用して問題を解決しましょう。
モンティホール問題
事前確率は次のように定義できます。
- 最初にドアAを選択するとします。
- P(H)= ⅓、⅓。 3つのドアすべての1/3。つまり、ドアが開いて山羊が現れる前に、車がいずれかのドアの後ろにある可能性が同じでした。
可能性は次のように定義できます。
-
P(D|H)、ここでイベントDは、モンティがドアBを選択し、その後ろに車がないことです。 - 車がドアAの後ろにある場合、
P(D|H)= 1/2-ドアBを選択する可能性が50%あり、ドアCを選択する可能性が50%あるためです。 - 車がドアBの後ろにある場合、
P(D|H)= 0です。これは、車がドアBの後ろにある場合、ドアBを選択する可能性が0%であるためです。 -
P(D|H)= 1車がCの後ろにあり、Aを選択した場合、彼がドアBを選択する確率は100%です。
P(H|D)に関心があります。これは、他のドアの1つの後ろにヤギが表示されている場合に、車がドアの後ろにある確率です。
後部P(H|D)から、AからドアCに切り替えると、勝つ確率が高くなることがわかります。

メトロポリス-ヘイスティングス
それでは、これまでに取り上げたすべてを組み合わせて、メトロポリス・ヘイスティングスがどのように機能するかを理解してみましょう。
Metropolis-Hastingsは、ベイズの定理を使用して、直接サンプリングが困難な複雑な分布の事後分布を取得します。
どのように? 基本的に、スペースからさまざまなサンプルをランダムに選択し、式(1)の確率の比率P(B)を調べているため、新しいサンプルが最後のサンプルよりも後方からのものである可能性が高いかどうかを確認します。キャンセル:
P(acceptance)=(P(newSample)*新しいサンプルの尤度)/(P(oldSample)*古いサンプルの尤度)
新しい各サンプルの「尤度」は、関数fによって決定されます。 そのため、 fはサンプリングする後方に比例する必要があります。
θ'を受け入れるか拒否するかを決定するには、新しく提案されたθ'ごとに次の比率を計算する必要があります。
ここで、θは古いサンプルですP(D| θ)はサンプルθの尤度です。
これをよりよく理解するために例を使用してみましょう。 データがあるが、それに適合する正規分布を見つけたいとしましょう。
X〜N(平均、標準)
次に、平均と標準の両方の事前確率を定義する必要があります。 簡単にするために、両方とも平均1と標準2の正規分布に従うと仮定します。
平均〜N(1、2)
std〜N(1、2)
ここで、いくつかのデータを生成し、真の平均とstdがそれぞれ0.5と1.2であると仮定しましょう。
import numpy as np import matplotlib.pyplot as plt import scipy.stats as st meanX = 1.5 stdX = 1.2 X = np.random.normal(meanX, stdX, size = 1000) _ = plt.hist(X, bins = 50)PyMC3
まず、 PyMC3というライブラリを使用してデータをモデル化し、平均と標準の事後分布を見つけましょう。
import pymc3 as pm with pm.Model() as model: mean = pm.Normal("mean", mu = 1, sigma = 2) std = pm.Normal("std", mu = 1, sigma = 2) x = pm.Normal("X", mu = mean, sigma = std, observed = X) step = pm.Metropolis() trace = pm.sample(5000, step = step)コードを見てみましょう。
まず、平均と標準の事前分布、つまり平均1と標準2の正規分布を定義します。
x = pm.Normal( "X"、mu =平均、シグマ= std、観測値= X)
この行では、関心のある変数を定義します。 以前に定義した平均と標準を取り、以前に計算した観測値も取ります。
結果を見てみましょう:
_ = plt.hist(trace['std'], bins = 50, label = "std") _ = plt.hist(trace['mean'], bins = 50, label = "mean") _ = plt.legend()stdは1.2を中心とし、平均は1.55です-かなり近いです!
メトロポリス・ヘイスティングスを理解するために、最初からやってみましょう。
スクラッチから
提案の生成
まず、メトロポリス・ヘイスティングスが何をしているのかを理解しましょう。 この記事の前半で、 「メトロポリス・ヘイスティングスは空間からさまざまなサンプルをランダムに選択する」と述べましたが、どのサンプルを選択するかをどのように知るのでしょうか。
これは、提案配布を使用して行います。 これは、現在受け入れられているサンプルを中心とした正規分布であり、STDは0.5です。 0.5がハイパーパラメータである場合、微調整できます。 提案のSTDが多いほど、現在受け入れられているサンプルからさらに検索されます。 これをコーディングしましょう。
分布の平均と標準を見つける必要があるため、この関数は現在受け入れられている平均と現在受け入れられている標準を取得し、両方の提案を返します。
def get_proposal(mean_current, std_current, proposal_width = 0.5): return np.random.normal(mean_current, proposal_width), \ np.random.normal(std_current, proposal_width)提案の承認/拒否
それでは、提案を受け入れるか拒否するロジックをコーディングしましょう。 これには、事前と尤度の2つの部分があります。
まず、提案が前から来る確率を計算しましょう。
def prior(mean, std, prior_mean, prior_std): return st.norm(prior_mean[0], prior_mean[1]).pdf(mean)* \ st.norm(prior_std[0], prior_std[1]).pdf(std)平均と標準を取得し、この平均と標準が定義した事前分布から得られた可能性を計算します。
尤度を計算する際に、私たちが見たデータが提案された分布からのものである可能性を計算します。
def likelihood(mean, std, data): return np.prod(st.norm(mean, std).pdf(X))したがって、データポイントごとに、提案された分布からのデータポイントの確率を乗算します。
ここで、これらの関数を現在の平均とstd、および提案された平均とstdに対して呼び出す必要があります。
prior_current = prior(mean_current, std_current, prior_mean, prior_std) likelihood_current = likelihood(mean_current, std_current, data) prior_proposal = prior(mean_proposal, std_proposal, prior_mean, prior_std) likelihood_proposal = likelihood(mean_proposal, std_proposal, data)コード全体:
def accept_proposal(mean_proposal, std_proposal, mean_current, \ std_current, prior_mean, prior_std, data): def prior(mean, std, prior_mean, prior_std): return st.norm(prior_mean[0], prior_mean[1]).pdf(mean)* \ st.norm(prior_std[0], prior_std[1]).pdf(std) def likelihood(mean, std, data): return np.prod(st.norm(mean, std).pdf(X)) prior_current = prior(mean_current, std_current, prior_mean, prior_std) likelihood_current = likelihood(mean_current, std_current, data) prior_proposal = prior(mean_proposal, std_proposal, prior_mean, prior_std) likelihood_proposal = likelihood(mean_proposal, std_proposal, data) return (prior_proposal * likelihood_proposal) / (prior_current * likelihood_current)次に、すべてを結び付けて必要な事後サンプルを生成する最終関数を作成しましょう。
後部の生成
ここで、上記で記述した関数を呼び出して、事後関数を生成します。
def get_trace(data, samples = 5000): mean_prior = 1 std_prior = 2 mean_current = mean_prior std_current = std_prior trace = { "mean": [mean_current], "std": [std_current] } for i in tqdm(range(samples)): mean_proposal, std_proposal = get_proposal(mean_current, std_current) acceptance_prob = accept_proposal(mean_proposal, std_proposal, mean_current, \ std_current, [mean_prior, std_prior], \ [mean_prior, std_prior], data) if np.random.rand() < acceptance_prob: mean_current = mean_proposal std_current = std_proposal trace['mean'].append(mean_current) trace['std'].append(std_current) return trace改善の余地
ログはあなたの友達です!
a * b = antilog(log(a) + log(b))およびa / b = antilog(log(a) - log(b)).
これは、非常に小さい確率を処理し、乗算するとゼロになるため、ログ確率を追加して問題を解決するため、私たちにとって有益です。
したがって、以前のコードは次のようになります。
def accept_proposal(mean_proposal, std_proposal, mean_current, \ std_current, prior_mean, prior_std, data): def prior(mean, std, prior_mean, prior_std): return st.norm(prior_mean[0], prior_mean[1]).logpdf(mean)+ \ st.norm(prior_std[0], prior_std[1]).logpdf(std) def likelihood(mean, std, data): return np.sum(st.norm(mean, std).logpdf(X)) prior_current = prior(mean_current, std_current, prior_mean, prior_std) likelihood_current = likelihood(mean_current, std_current, data) prior_proposal = prior(mean_proposal, std_proposal, prior_mean, prior_std) likelihood_proposal = likelihood(mean_proposal, std_proposal, data) return (prior_proposal + likelihood_proposal) - (prior_current + likelihood_current)受け入れ確率のログを返すので、次のようになります。
if np.random.rand() < acceptance_prob:
になる:
if math.log(np.random.rand()) < acceptance_prob:
新しいコードを実行して、結果をプロットしてみましょう。
_ = plt.hist(trace['std'], bins = 50, label = "std") _ = plt.hist(trace['mean'], bins = 50, label = "mean") _ = plt.legend()ご覧のとおり、標準は1.2を中心とし、平均は1.5を中心としています。 やりました!
前進する
これまでに、メトロポリス・ヘイスティングスがどのように機能するかを理解し、どこで使用できるのか疑問に思われるかもしれません。
ベイズのハッカーのための方法は、確率的プログラミングを説明する優れた本です。ベイズの定理とその応用について詳しく知りたい場合は、 ThinkBayesはAllenB.Downeyによる優れた本です。
読んでいただきありがとうございます。この記事がベイズ統計の驚くべき世界を発見するきっかけになることを願っています。
