Métodos MCMC: Metropolis-Hastings e Inferencia Bayesiana
Publicado: 2022-03-11Dejemos de lado la definición básica: los métodos de Markov Chain Monte Carlo (MCMC) nos permiten calcular muestras de una distribución aunque no podamos calcularla.
¿Qué significa esto? Retrocedamos y hablemos sobre el muestreo de Monte Carlo.
Muestreo de Montecarlo
¿Qué son los métodos de Montecarlo?
“Los métodos de Monte Carlo, o experimentos de Monte Carlo, son una amplia clase de algoritmos computacionales que se basan en muestreos aleatorios repetidos para obtener resultados numéricos”. (Wikipedia)
Analicemos eso.
Ejemplo 1: Estimación del área
Imagina que tienes una forma irregular, como la forma que se presenta a continuación:
Y tiene la tarea de determinar el área encerrada por esta forma. Uno de los métodos que puede usar es hacer pequeños cuadrados en la forma, contar los cuadrados y eso le dará una aproximación bastante precisa del área. Sin embargo, eso es difícil y requiere mucho tiempo.
Muestreo de Monte Carlo al rescate!
Primero, dibujamos un gran cuadrado de un área conocida alrededor de la forma, por ejemplo de 50 cm2. Ahora "colgamos" este cuadrado y comenzamos a lanzar dardos al azar a la forma.
Luego, contamos el número total de dardos en el rectángulo y el número de dardos en la forma que nos interesa. Supongamos que el número total de "dardos" usados fue 100 y que 22 de ellos terminaron dentro de la forma. Ahora el área se puede calcular con la fórmula simple:
área de la forma = área del cuadrado *(número de dardos en la forma) / (número de dardos en el cuadrado)
Entonces, en nuestro caso, esto se reduce a:
área de forma = 50 * 22/100 = 11 cm2
Si multiplicamos el número de “dardos” por un factor de 10, esta aproximación se acerca mucho a la respuesta real:
área de forma = 50 * 280/1000 = 14 cm2
Así es como desglosamos tareas complicadas, como la anterior, utilizando el muestreo de Monte Carlo.
La Ley de los Grandes Números
La aproximación del área fue más cercana cuantos más dardos lanzamos, y esto se debe a la Ley de los Grandes Números:
“La ley de los grandes números es un teorema que describe el resultado de realizar el mismo experimento un gran número de veces. De acuerdo con la ley, el promedio de los resultados obtenidos de un gran número de ensayos debe estar cerca del valor esperado, y tenderá a acercarse a medida que se realicen más ensayos”.
Esto nos lleva a nuestro próximo ejemplo, el famoso problema de Monty Hall.
Ejemplo 2: El problema de Monty Hall
El problema de Monty Hall es un acertijo muy famoso:
“Hay tres puertas, una tiene un auto detrás, las otras tienen una cabra detrás. Eliges una puerta, el anfitrión abre una puerta diferente y te muestra que hay una cabra detrás. Luego te pregunta si quieres cambiar tu decisión. ¿Vos si? ¿Por qué? ¿Por qué no?"
Lo primero que te viene a la mente es que las posibilidades de ganar son iguales tanto si cambias como si no, pero eso no es cierto. Hagamos un diagrama de flujo simple para demostrar lo mismo.
Suponiendo que el coche está detrás de la puerta 3:
Por lo tanto, si cambia, gana ⅔ veces, y si no cambia, gana solo ⅓ veces.
Resolvamos esto usando muestreo.
wins = [] for i in range(int(10e6)): car_door = assign_car_door() choice = random.randint(0, 2) opened_door = assign_door_to_open(car_door) did_he_win = win_or_lose(choice, car_door, opened_door, switch = False) wins.append(did_he_win) print(sum(wins)/len(wins)) La función assign_car_door() es solo un generador de números aleatorios que selecciona una puerta 0, 1 o 2, detrás de la cual hay un automóvil. El uso assign_door_to_open selecciona una puerta que tiene una cabra detrás y no es la que seleccionó, y el anfitrión la abre. win_or_lose devuelve true o false , indicando si ganó el auto o no, toma un "interruptor" bool que dice si cambió la puerta o no.
Ejecutemos esta simulación 10 millones de veces:
- Probabilidad de ganar si no cambia: 0.334134
- Probabilidad de ganar si cambia: 0.667255
Esto está muy cerca de las respuestas que nos dio el diagrama de flujo.
De hecho, cuanto más ejecutamos esta simulación, más se acerca la respuesta al valor real, lo que valida la ley de los grandes números:
Lo mismo se puede ver en esta tabla:
| Ejecución de simulaciones | Probabilidad de ganar si cambia | Probabilidad de ganar si no cambia |
| 10 | 0.6 | 0.2 |
| 10^2 | 0,63 | 0.33 |
| 10^3 | 0.661 | 0.333 |
| 10^4 | 0.6683 | 0.3236 |
| 10^5 | 0.66762 | 0.33171 |
| 10^6 | 0.667255 | 0.334134 |
| 10^7 | 0.6668756 | 0.3332821 |
La forma de pensar bayesiana
“El frecuentista, conocido como la versión más clásica de la estadística, asume que la probabilidad es la frecuencia de eventos a largo plazo (de ahí el título otorgado)”.
“La estadística bayesiana es una teoría en el campo de la estadística basada en la interpretación bayesiana de la probabilidad, donde la probabilidad expresa un grado de creencia en un evento. El grado de creencia puede basarse en el conocimiento previo sobre el evento, como los resultados de experimentos anteriores, o en creencias personales sobre el evento”. - de Programación Probabilística y Métodos Bayesianos para Hackers
¿Qué significa esto?
En la forma de pensar frecuentista, observamos las probabilidades a largo plazo. Cuando un frecuentador dice que hay un 0,001% de posibilidades de que ocurra un accidente de coche, quiere decir que, si consideramos infinitos viajes en coche, el 0,001% de ellos terminarán en un accidente.
Una mentalidad bayesiana es diferente, ya que comenzamos con una creencia previa. Si hablamos de una creencia de 0, significa que tu creencia es que el evento nunca sucederá; por el contrario, una creencia de 1 significa que está seguro de que sucederá.
Luego, una vez que comenzamos a observar los datos, actualizamos esta creencia para tener en cuenta los datos. Cómo hacemos esto? Usando el teorema de Bayes.
Teorema de Bayes
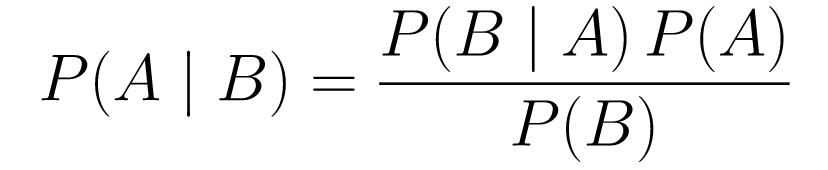 ....(1)
....(1)Vamos a desglosarlo.
-
P(A | B)nos da la probabilidad del evento A dado el evento B. Esta es la posterior, B son los datos que observamos, por lo que esencialmente estamos diciendo cuál es la probabilidad de que ocurra un evento, considerando los datos que observamos. -
P(A)es lo previo, nuestra creencia de que el evento A sucederá. -
P(B | A)es la probabilidad, ¿cuál es la probabilidad de que observemos los datos dado que A es verdadero?
Veamos un ejemplo, la prueba de detección del cáncer.
Probabilidad de cáncer
Digamos que un paciente va a hacerse una mamografía y la mamografía da positivo. ¿Cuál es la probabilidad de que el paciente realmente tenga cáncer?
Definamos las probabilidades:
- El 1% de las mujeres tienen cáncer de mama.
- Las mamografías detectan el cáncer el 80% de las veces cuando en realidad está presente.
- El 9,6% de las mamografías informan falsamente que tiene cáncer cuando en realidad no lo tiene.
Entonces, si dijera que si una mamografía resultó positiva, significa que hay un 80% de probabilidad de que tenga cáncer, eso sería incorrecto. No tomarías en consideración que tener cáncer es un evento raro, es decir, que solo el 1% de las mujeres tienen cáncer de mama. Necesitamos tomar esto como algo previo, y aquí es donde entra en juego el teorema de Bayes:
P(C+ | T+) =(P(T+|C+)*P(C+))/P(T+)
-
P(C+ | T+): Esta es la probabilidad de que haya cáncer, dado que la prueba fue positiva, esto es lo que nos interesa. -
P(T+ | C+): Esta es la probabilidad de que la prueba sea positiva, dado que hay cáncer, esto, como se discutió anteriormente, es igual a 80% = 0.8. -
P(C+): Esta es la probabilidad previa, la probabilidad de que un individuo tenga cáncer, que es igual a 1% = 0,01. -
P(T+): Esta es la probabilidad de que la prueba sea positiva, pase lo que pase, por lo que tiene dos componentes: P(T+) = P(T+|C-) P(C-)+P(T+|C+) P (C+) -
P(T+ | C-): Esta es la probabilidad de que la prueba resulte positiva pero no haya cáncer, esto está dado por 0.096. -
P(C-): Esta es la probabilidad de no tener cáncer ya que la probabilidad de tener cáncer es del 1%, esto es igual al 99% = 0.99. -
P(T+ | C+): Esta es la probabilidad de que la prueba resulte positiva, dado que tienes cáncer, esto es igual a 80% = 0.8. -
P(C+): Esta es la probabilidad de tener cáncer, que es igual a 1% = 0,01.
Conectando todo esto en la fórmula original:
Entonces, dado que la mamografía salió positiva, hay un 7,76% de posibilidades de que la paciente tenga cáncer. Puede parecer extraño al principio, pero tiene sentido. La prueba da un falso positivo el 9,6% de las veces (bastante alto), por lo que habrá muchos falsos positivos en una población determinada. Para una enfermedad rara, la mayoría de los resultados positivos de las pruebas serán incorrectos.
Repasemos ahora el problema de Monty Hall y resolvámoslo usando el teorema de Bayes.
Problema de Monty Hall
Los anteriores se pueden definir como:
- Suponga que elige la puerta A como su elección al principio.
- P(H) = ⅓, ⅓. ⅓ para las tres puertas, lo que significa que antes de que se abriera la puerta y se revelara la cabra, había las mismas posibilidades de que el automóvil estuviera detrás de cualquiera de ellas.
La probabilidad se puede definir como:

-
P(D|H), donde el evento D es que Monty elige la puerta B y no hay ningún auto detrás. -
P(D|H)= 1/2 si el coche está detrás de la puerta A, ya que hay un 50 % de posibilidades de que elija la puerta B y un 50 % de posibilidades de que elija la puerta C. -
P(D|H)= 0 si el coche está detrás de la puerta B, ya que hay un 0% de probabilidad de que elija la puerta B si el coche está detrás. -
P(D|H)= 1 si el coche está detrás de C y eliges A, hay un 100% de probabilidad de que elija la puerta B.
Nos interesa P(H|D) , que es la probabilidad de que el coche esté detrás de una puerta dado que nos muestra una cabra detrás de una de las otras puertas.
Se puede ver desde la parte posterior, P(H|D) , que cambiar a la puerta C desde A aumentará la probabilidad de ganar.
Metrópolis-Hastings
Ahora, combinemos todo lo que cubrimos hasta ahora e intentemos entender cómo funciona Metropolis-Hastings.
Metropolis-Hastings usa el teorema de Bayes para obtener la distribución posterior de una distribución compleja, de la cual el muestreo directo es difícil.
¿Cómo? Esencialmente, selecciona aleatoriamente diferentes muestras de un espacio y comprueba si es más probable que la nueva muestra sea posterior a la última muestra, ya que estamos viendo la relación de probabilidades, P(B) en la ecuación (1), se obtiene cancelado:
P(aceptación) = ( P(muestra nueva) * Probabilidad de muestra nueva) / (P(Muestra antigua) * Probabilidad de muestra antigua)
La "probabilidad" de cada nueva muestra se decide por la función f . Es por eso que f debe ser proporcional a la parte posterior de la que queremos muestrear.
Para decidir si se acepta o rechaza θ′, se debe calcular la siguiente relación para cada nuevo θ' propuesto:
Donde θ es la muestra anterior, P(D| θ) es la probabilidad de la muestra θ.
Usemos un ejemplo para entender esto mejor. Digamos que tiene datos pero quiere encontrar la distribución normal que se ajuste a ellos, entonces:
X ~ N (media, estándar)
Ahora necesitamos definir las prioridades para la media y la estándar. Para simplificar, supondremos que ambos siguen una distribución normal con media 1 y estándar 2:
Media ~ N(1, 2)
estándar ~ N(1, 2)
Ahora, generemos algunos datos y supongamos que la verdadera media y el estándar son 0,5 y 1,2, respectivamente.
import numpy as np import matplotlib.pyplot as plt import scipy.stats as st meanX = 1.5 stdX = 1.2 X = np.random.normal(meanX, stdX, size = 1000) _ = plt.hist(X, bins = 50)PyMC3
Primero usemos una biblioteca llamada PyMC3 para modelar los datos y encontrar la distribución posterior para la media y la estándar.
import pymc3 as pm with pm.Model() as model: mean = pm.Normal("mean", mu = 1, sigma = 2) std = pm.Normal("std", mu = 1, sigma = 2) x = pm.Normal("X", mu = mean, sigma = std, observed = X) step = pm.Metropolis() trace = pm.sample(5000, step = step)Repasemos el código.
Primero, definimos el prior para la media y estándar, es decir, una normal con media 1 y estándar 2.
x = pm.Normal(“X”, mu = media, sigma = std, observado = X)
En esta línea definimos la variable que nos interesa; toma la media y el estándar que definimos anteriormente, también toma los valores observados que calculamos anteriormente.
Veamos los resultados:
_ = plt.hist(trace['std'], bins = 50, label = "std") _ = plt.hist(trace['mean'], bins = 50, label = "mean") _ = plt.legend()El std se centra alrededor de 1.2, y la media está en 1.55, ¡bastante cerca!
Ahora hagámoslo desde cero para entender Metropolis-Hastings.
desde cero
Generación de una propuesta
Primero, entendamos qué hace Metropolis-Hastings. Anteriormente en este artículo, dijimos: "Metropolis-Hastings selecciona aleatoriamente diferentes muestras de un espacio", pero ¿cómo sabe qué muestra seleccionar?
Lo hace utilizando la distribución propuesta. Es una distribución normal centrada en la muestra actualmente aceptada y tiene un STD de 0.5. Donde 0.5 es un hiperparámetro, podemos ajustar; cuanto mayor sea el STD de la propuesta, más buscará en la muestra actualmente aceptada. Vamos a codificar esto.
Dado que tenemos que encontrar la media y el estándar de la distribución, esta función tomará la media y el estándar actualmente aceptados y devolverá propuestas para ambos.
def get_proposal(mean_current, std_current, proposal_width = 0.5): return np.random.normal(mean_current, proposal_width), \ np.random.normal(std_current, proposal_width)Aceptar/rechazar una propuesta
Ahora, codifiquemos la lógica que acepta o rechaza la propuesta. Consta de dos partes: la previa y la de verosimilitud .
Primero, calculemos la probabilidad de que la propuesta provenga de la previa:
def prior(mean, std, prior_mean, prior_std): return st.norm(prior_mean[0], prior_mean[1]).pdf(mean)* \ st.norm(prior_std[0], prior_std[1]).pdf(std)Simplemente toma la media y la desviación estándar y calcula la probabilidad de que esta media y la desviación estándar provengan de la distribución anterior que definimos.
Al calcular la probabilidad, calculamos la probabilidad de que los datos que vimos provengan de la distribución propuesta.
def likelihood(mean, std, data): return np.prod(st.norm(mean, std).pdf(X))Entonces, para cada punto de datos, multiplicamos la probabilidad de que ese punto de datos provenga de la distribución propuesta.
Ahora, necesitamos llamar a estas funciones para la media y estándar actual y para la media y estándar propuesta.
prior_current = prior(mean_current, std_current, prior_mean, prior_std) likelihood_current = likelihood(mean_current, std_current, data) prior_proposal = prior(mean_proposal, std_proposal, prior_mean, prior_std) likelihood_proposal = likelihood(mean_proposal, std_proposal, data)Todo el código:
def accept_proposal(mean_proposal, std_proposal, mean_current, \ std_current, prior_mean, prior_std, data): def prior(mean, std, prior_mean, prior_std): return st.norm(prior_mean[0], prior_mean[1]).pdf(mean)* \ st.norm(prior_std[0], prior_std[1]).pdf(std) def likelihood(mean, std, data): return np.prod(st.norm(mean, std).pdf(X)) prior_current = prior(mean_current, std_current, prior_mean, prior_std) likelihood_current = likelihood(mean_current, std_current, data) prior_proposal = prior(mean_proposal, std_proposal, prior_mean, prior_std) likelihood_proposal = likelihood(mean_proposal, std_proposal, data) return (prior_proposal * likelihood_proposal) / (prior_current * likelihood_current)Ahora, creemos la función final que unirá todo y generará las muestras posteriores que necesitamos.
Generando el Posterior
¡Ahora, llamamos a las funciones que hemos escrito arriba y generamos el posterior!
def get_trace(data, samples = 5000): mean_prior = 1 std_prior = 2 mean_current = mean_prior std_current = std_prior trace = { "mean": [mean_current], "std": [std_current] } for i in tqdm(range(samples)): mean_proposal, std_proposal = get_proposal(mean_current, std_current) acceptance_prob = accept_proposal(mean_proposal, std_proposal, mean_current, \ std_current, [mean_prior, std_prior], \ [mean_prior, std_prior], data) if np.random.rand() < acceptance_prob: mean_current = mean_proposal std_current = std_proposal trace['mean'].append(mean_current) trace['std'].append(std_current) return traceMargen de mejora
¡Log es tu amigo!
Recuerde a * b = antilog(log(a) + log(b)) y a / b = antilog(log(a) - log(b)).
Esto es beneficioso para nosotros porque estaremos lidiando con probabilidades muy pequeñas, multiplicando lo que dará como resultado cero, por lo que preferiremos agregar el log prob, ¡problema resuelto!
Entonces, nuestro código anterior se convierte en:
def accept_proposal(mean_proposal, std_proposal, mean_current, \ std_current, prior_mean, prior_std, data): def prior(mean, std, prior_mean, prior_std): return st.norm(prior_mean[0], prior_mean[1]).logpdf(mean)+ \ st.norm(prior_std[0], prior_std[1]).logpdf(std) def likelihood(mean, std, data): return np.sum(st.norm(mean, std).logpdf(X)) prior_current = prior(mean_current, std_current, prior_mean, prior_std) likelihood_current = likelihood(mean_current, std_current, data) prior_proposal = prior(mean_proposal, std_proposal, prior_mean, prior_std) likelihood_proposal = likelihood(mean_proposal, std_proposal, data) return (prior_proposal + likelihood_proposal) - (prior_current + likelihood_current)Como estamos devolviendo el logaritmo de la probabilidad de aceptación:
if np.random.rand() < acceptance_prob:
se convierte en:
if math.log(np.random.rand()) < acceptance_prob:
Ejecutemos el nuevo código y tracemos los resultados.
_ = plt.hist(trace['std'], bins = 50, label = "std") _ = plt.hist(trace['mean'], bins = 50, label = "mean") _ = plt.legend()Como puede ver, el estándar está centrado en 1.2 y la media en 1.5. ¡Lo hicimos!
Avanzando
A estas alturas, es de esperar que comprenda cómo funciona Metropolis-Hastings y es posible que se pregunte dónde puede usarlo.
Bueno, Bayesian Methods for Hackers es un libro excelente que explica la programación probabilística, y si quieres aprender más sobre el teorema de Bayes y sus aplicaciones, Think Bayes es un gran libro de Allen B. Downey.
Gracias por leer, y espero que este artículo te anime a descubrir el asombroso mundo de las estadísticas bayesianas.
