MCMC-Methoden: Metropolis-Hastings und Bayes'sche Inferenz
Veröffentlicht: 2022-03-11Lassen Sie uns die grundlegende Definition aus dem Weg räumen: Markov Chain Monte Carlo (MCMC)-Methoden ermöglichen es uns, Stichproben aus einer Verteilung zu berechnen, obwohl wir sie nicht berechnen können.
Was bedeutet das? Lassen Sie uns zurückgehen und über Monte-Carlo-Sampling sprechen.
Monte-Carlo-Sampling
Was sind Monte-Carlo-Methoden?
„Monte-Carlo-Methoden oder Monte-Carlo-Experimente sind eine breite Klasse von Rechenalgorithmen, die sich auf wiederholte Zufallsstichproben stützen, um numerische Ergebnisse zu erhalten.“ (Wikipedia)
Lassen Sie uns das aufschlüsseln.
Beispiel 1: Flächenschätzung
Stellen Sie sich vor, Sie haben eine unregelmäßige Form, wie die unten dargestellte:
Und Sie haben die Aufgabe, die von dieser Form eingeschlossene Fläche zu bestimmen. Eine der Methoden, die Sie verwenden können, besteht darin, kleine Quadrate in der Form zu machen, die Quadrate zu zählen, und das wird Ihnen eine ziemlich genaue Annäherung an die Fläche geben. Das ist jedoch schwierig und zeitaufwändig.
Monte-Carlo-Sampling zur Rettung!
Zuerst zeichnen wir ein großes Quadrat mit bekannter Fläche um die Form herum, zum Beispiel 50 cm2. Jetzt „hängen“ wir dieses Quadrat und fangen an, willkürlich Pfeile auf die Form zu werfen.
Als nächstes zählen wir die Gesamtzahl der Pfeile im Rechteck und die Anzahl der Pfeile in der Form, die uns interessiert. Nehmen wir an, dass die Gesamtzahl der verwendeten „Pfeile“ 100 war und dass 22 davon in der Form landeten. Nun kann die Fläche nach der einfachen Formel berechnet werden:
Fläche der Form = Fläche des Quadrats * (Anzahl der Abnäher in der Form) / (Anzahl der Abnäher im Quadrat)
In unserem Fall läuft es also auf Folgendes hinaus:
Formfläche = 50 * 22/100 = 11 cm2
Wenn wir die Anzahl der „Pfeile“ mit dem Faktor 10 multiplizieren, kommt diese Annäherung der wirklichen Antwort sehr nahe:
Formfläche = 50 * 280/1000 = 14 cm2
Auf diese Weise zerlegen wir komplizierte Aufgaben, wie die oben angegebene, mithilfe von Monte-Carlo-Sampling.
Das Gesetz der großen Zahlen
Die Flächenannäherung war umso enger, je mehr Pfeile wir geworfen haben, und das liegt am Gesetz der großen Zahlen:
„Das Gesetz der großen Zahlen ist ein Theorem, das das Ergebnis beschreibt, wenn dasselbe Experiment viele Male durchgeführt wird. Laut Gesetz sollte der Durchschnitt der Ergebnisse aus einer großen Anzahl von Versuchen nahe am erwarteten Wert liegen und nähert sich tendenziell an, je mehr Versuche durchgeführt werden.“
Dies bringt uns zu unserem nächsten Beispiel, dem berühmten Monty-Hall-Problem.
Beispiel 2: Das Monty-Hall-Problem
Das Monty-Hall-Problem ist eine sehr berühmte Denksportaufgabe:
„Es gibt drei Türen, hinter einer steht ein Auto, hinter den anderen eine Ziege. Sie wählen eine Tür, der Gastgeber öffnet eine andere Tür und zeigt Ihnen, dass sich dahinter eine Ziege befindet. Er fragt Sie dann, ob Sie Ihre Entscheidung ändern möchten. Tust du? Warum? Warum nicht?"
Das erste, was Ihnen in den Sinn kommt, ist, dass die Gewinnchancen gleich sind, egal ob Sie wechseln oder nicht, aber das stimmt nicht. Lassen Sie uns ein einfaches Flussdiagramm erstellen, um dasselbe zu demonstrieren.
Angenommen, das Auto steht hinter Tür 3:
Wenn Sie also wechseln, gewinnen Sie ⅔ Mal, und wenn Sie nicht wechseln, gewinnen Sie nur ⅓ Mal.
Lassen Sie uns dies lösen, indem wir Sampling verwenden.
wins = [] for i in range(int(10e6)): car_door = assign_car_door() choice = random.randint(0, 2) opened_door = assign_door_to_open(car_door) did_he_win = win_or_lose(choice, car_door, opened_door, switch = False) wins.append(did_he_win) print(sum(wins)/len(wins)) Die Funktion assign_car_door() ist nur ein Zufallszahlengenerator, der eine Tür 0, 1 oder 2 auswählt, hinter der sich ein Auto befindet. Durch die Verwendung assign_door_to_open wird eine Tür ausgewählt, hinter der sich eine Ziege befindet und die nicht die von Ihnen ausgewählte ist, und der Host öffnet sie. win_or_lose gibt true oder false zurück, was angibt, ob Sie das Auto gewonnen haben oder nicht, es braucht einen boolschen „switch“, der angibt, ob Sie die Tür gewechselt haben oder nicht.
Lassen Sie uns diese Simulation 10 Millionen Mal ausführen:
- Gewinnwahrscheinlichkeit, wenn Sie nicht wechseln: 0,334134
- Gewinnwahrscheinlichkeit bei Wechsel: 0,667255
Dies kommt den Antworten, die uns das Flussdiagramm gegeben hat, sehr nahe.
Je öfter wir diese Simulation ausführen, desto näher kommt die Antwort dem wahren Wert, wodurch das Gesetz der großen Zahlen bestätigt wird:
Das Gleiche ist aus dieser Tabelle ersichtlich:
| Simulationen laufen | Wahrscheinlichkeit zu gewinnen, wenn Sie wechseln | Gewinnwahrscheinlichkeit, wenn Sie nicht wechseln |
| 10 | 0,6 | 0,2 |
| 10^2 | 0,63 | 0,33 |
| 10^3 | 0,661 | 0,333 |
| 10^4 | 0,6683 | 0,3236 |
| 10^5 | 0,66762 | 0,33171 |
| 10^6 | 0,667255 | 0,334134 |
| 10^7 | 0,6668756 | 0,3332821 |
Die Bayessche Denkweise
„Häufiger, bekannt als die klassischere Version der Statistik, gehen davon aus, dass die Wahrscheinlichkeit die langfristige Häufigkeit von Ereignissen ist (daher der verliehene Titel).“
„Bayessche Statistik ist eine Theorie auf dem Gebiet der Statistik, die auf der Bayesschen Interpretation der Wahrscheinlichkeit basiert, wobei die Wahrscheinlichkeit einen Grad des Glaubens an ein Ereignis ausdrückt. Der Grad der Überzeugung kann auf Vorkenntnissen über das Ereignis beruhen, wie z. B. den Ergebnissen früherer Experimente, oder auf persönlichen Überzeugungen über das Ereignis.“ - von Probabilistic Programming und Bayesian Methods for Hackers
Was bedeutet das?
In frequentistischer Denkweise betrachten wir Wahrscheinlichkeiten auf lange Sicht. Wenn ein Frequentist sagt, dass die Wahrscheinlichkeit eines Autounfalls bei 0,001 % liegt, bedeutet das, wenn wir unendlich viele Autofahrten betrachten, dass 0,001 % davon in einem Unfall enden.
Eine bayessche Denkweise ist anders, da wir mit einem Prior, einer Überzeugung, beginnen. Wenn wir von einer Überzeugung von 0 sprechen, bedeutet dies, dass Sie glauben, dass das Ereignis niemals eintreten wird; Umgekehrt bedeutet eine Überzeugung von 1, dass Sie sicher sind, dass es passieren wird.
Sobald wir dann beginnen, Daten zu beobachten, aktualisieren wir diese Überzeugung, um die Daten zu berücksichtigen. Wie machen wir das? Unter Verwendung des Satzes von Bayes.
Satz von Bayes
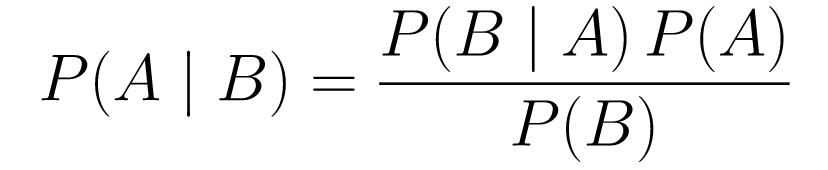 ....(1)
....(1)Lass es uns aufschlüsseln.
-
P(A | B)gibt uns die Wahrscheinlichkeit des Ereignisses A bei Ereignis B. Dies ist das Posterior, B sind die Daten, die wir beobachtet haben, also sagen wir im Wesentlichen, wie hoch die Wahrscheinlichkeit ist, dass ein Ereignis eintritt, wenn man die Daten berücksichtigt, die wir beobachtet haben. -
P(A)ist der Prior, unsere Überzeugung, dass Ereignis A eintreten wird. -
P(B | A)ist die Wahrscheinlichkeit, wie groß die Wahrscheinlichkeit ist, dass wir die Daten beobachten, wenn A wahr ist.
Schauen wir uns ein Beispiel an, den Krebsvorsorgetest.
Wahrscheinlichkeit von Krebs
Nehmen wir an, eine Patientin geht zur Mammographie und die Mammographie kommt positiv zurück. Wie groß ist die Wahrscheinlichkeit, dass der Patient tatsächlich Krebs hat?
Lassen Sie uns die Wahrscheinlichkeiten definieren:
- 1% der Frauen haben Brustkrebs.
- Mammographien erkennen Krebs in 80 % der Fälle, wenn er tatsächlich vorhanden ist.
- 9,6 % der Mammographien geben fälschlicherweise an, dass Sie Krebs haben, obwohl Sie ihn eigentlich gar nicht haben.
Wenn Sie also sagen würden, dass bei einem positiven Ergebnis einer Mammographie eine 80-prozentige Wahrscheinlichkeit besteht, dass Sie Krebs haben, wäre das falsch. Sie würden nicht berücksichtigen, dass Krebs ein seltenes Ereignis ist, dh dass nur 1 % der Frauen Brustkrebs haben. Wir müssen dies als voraussetzen, und hier kommt das Bayes-Theorem ins Spiel:
P(C+ | T+) = (P(T+|C+)*P(C+))/P(T+)
-
P(C+ | T+): Dies ist die Wahrscheinlichkeit, dass Krebs da ist, vorausgesetzt, der Test war positiv, das interessiert uns. -
P(T+ | C+): Dies ist die Wahrscheinlichkeit, dass der Test positiv ist, vorausgesetzt, dass Krebs vorliegt, dies ist, wie oben diskutiert, gleich 80 % = 0,8. -
P(C+): Dies ist die vorherige Wahrscheinlichkeit, die Wahrscheinlichkeit, dass eine Person Krebs hat, die gleich 1 % = 0,01 ist. -
P(T+): Dies ist die Wahrscheinlichkeit, dass der Test positiv ist, egal was passiert, also hat er zwei Komponenten: P(T+) = P(T+|C-) P(C-)+P(T+|C+) P (C+) -
P(T+ | C-): Dies ist die Wahrscheinlichkeit, dass der Test positiv ausgefallen ist, aber kein Krebs vorliegt, diese wird mit 0,096 angegeben. -
P(C-): Dies ist die Wahrscheinlichkeit, keinen Krebs zu haben, da die Wahrscheinlichkeit, Krebs zu haben, 1 % beträgt, entspricht dies 99 % = 0,99. -
P(T+ | C+): Dies ist die Wahrscheinlichkeit, dass der Test positiv ausgefallen ist, vorausgesetzt, Sie haben Krebs, dies entspricht 80 % = 0,8. -
P(C+): Dies ist die Wahrscheinlichkeit, an Krebs zu erkranken, die gleich 1 % = 0,01 ist.
Setzen Sie all dies in die ursprüngliche Formel ein:
Wenn also die Mammographie positiv ausgefallen ist, besteht eine Wahrscheinlichkeit von 7,76 %, dass die Patientin Krebs hat. Es mag auf den ersten Blick seltsam erscheinen, aber es macht Sinn. Der Test ergibt in 9,6 % der Fälle ein falsch positives Ergebnis (ziemlich hoch), sodass es in einer bestimmten Population viele falsch positive Ergebnisse geben wird. Bei einer seltenen Krankheit sind die meisten positiven Testergebnisse falsch.
Betrachten wir nun das Monty-Hall-Problem noch einmal und lösen es mit dem Bayes-Theorem.
Monty-Hall-Problem
Die Priors können wie folgt definiert werden:

- Angenommen, Sie wählen am Anfang Tür A als Ihre Wahl.
- P(H) = ⅓, ⅓. ⅓ für alle drei Türen, was bedeutet, dass bevor die Tür geöffnet wurde und die Ziege auftauchte, die gleiche Wahrscheinlichkeit bestand, dass sich das Auto hinter einer von ihnen befand.
Die Wahrscheinlichkeit kann wie folgt definiert werden:
-
P(D|H), wobei Ereignis D darin besteht, dass Monty Tür B wählt und sich kein Auto dahinter befindet. -
P(D|H)= 1/2 wenn sich das Auto hinter Tür A befindet – da es eine 50% Chance gibt, dass er Tür B wählt und eine 50% Chance, dass er Tür C wählt. -
P(D|H)= 0, wenn sich das Auto hinter Tür B befindet, da es eine Wahrscheinlichkeit von 0 % gibt, dass er Tür B wählt, wenn sich das Auto dahinter befindet. -
P(D|H)= 1 Wenn das Auto hinter C steht und Sie A wählen, besteht eine 100%ige Wahrscheinlichkeit, dass er Tür B wählt.
Uns interessiert P(H|D) , also die Wahrscheinlichkeit, dass sich das Auto hinter einer Tür befindet, da es uns hinter einer der anderen Türen eine Ziege zeigt.
Aus dem Posterior P(H|D) ist ersichtlich, dass das Wechseln von A zu Tür C die Gewinnwahrscheinlichkeit erhöht.
Metropole-Hastings
Lassen Sie uns nun alles, was wir bisher behandelt haben, kombinieren und versuchen zu verstehen, wie Metropolis-Hastings funktioniert.
Metropolis-Hastings verwendet das Bayes-Theorem, um die A-Posteriori-Verteilung einer komplexen Verteilung zu erhalten, aus der eine direkte Stichprobenziehung schwierig ist.
Wie? Im Wesentlichen wählt es zufällig verschiedene Stichproben aus einem Raum aus und prüft, ob die neue Stichprobe wahrscheinlicher von der hinteren Stichprobe stammt als die letzte Stichprobe, da wir das Verhältnis der Wahrscheinlichkeiten, P(B) in Gleichung (1), erhalten abgesagt:
P(Akzeptanz) = ( P(newSample) * Wahrscheinlichkeit der neuen Probe) / (P(oldSample) * Wahrscheinlichkeit der alten Probe)
Die „Wahrscheinlichkeit“ jeder neuen Stichprobe wird durch die Funktion f bestimmt . Aus diesem Grund muss f proportional zu dem Posterior sein, von dem wir abtasten möchten.
Um zu entscheiden, ob θ′ akzeptiert oder abgelehnt werden soll, muss das folgende Verhältnis für jedes neu vorgeschlagene θ' berechnet werden:
Wobei θ die alte Probe ist, ist P(D| θ) die Wahrscheinlichkeit der Probe θ.
Lassen Sie uns ein Beispiel verwenden, um dies besser zu verstehen. Angenommen, Sie haben Daten, möchten aber die passende Normalverteilung herausfinden, also:
X ~ N (Mittelwert, Standard)
Jetzt müssen wir die Priors für den Mittelwert und die Standardwerte definieren. Der Einfachheit halber gehen wir davon aus, dass beide einer Normalverteilung mit Mittelwert 1 und Standardwert 2 folgen:
Mittelwert ~ N(1, 2)
Standard ~ N(1, 2)
Lassen Sie uns nun einige Daten generieren und davon ausgehen, dass der wahre Mittelwert und der Standardwert 0,5 bzw. 1,2 betragen.
import numpy as np import matplotlib.pyplot as plt import scipy.stats as st meanX = 1.5 stdX = 1.2 X = np.random.normal(meanX, stdX, size = 1000) _ = plt.hist(X, bins = 50)PyMC3
Lassen Sie uns zuerst eine Bibliothek namens PyMC3 verwenden, um die Daten zu modellieren und die A-posteriori-Verteilung für Mittelwert und Standard zu finden.
import pymc3 as pm with pm.Model() as model: mean = pm.Normal("mean", mu = 1, sigma = 2) std = pm.Normal("std", mu = 1, sigma = 2) x = pm.Normal("X", mu = mean, sigma = std, observed = X) step = pm.Metropolis() trace = pm.sample(5000, step = step)Lassen Sie uns den Code durchgehen.
Zuerst definieren wir den Prior für Mittelwert und Standardwert, dh einen Normalwert mit Mittelwert 1 und Standardwert 2.
x = pm.Normal(“X”, mu = Mittelwert, Sigma = Standard, beobachtet = X)
In dieser Zeile definieren wir die Variable, die uns interessiert; es nimmt den Mittelwert und den std, den wir zuvor definiert haben, es nimmt auch beobachtete Werte, die wir zuvor berechnet haben.
Schauen wir uns die Ergebnisse an:
_ = plt.hist(trace['std'], bins = 50, label = "std") _ = plt.hist(trace['mean'], bins = 50, label = "mean") _ = plt.legend()Der std ist um 1,2 herum zentriert, und der Mittelwert liegt bei 1,55 – ziemlich nah dran!
Machen wir es jetzt von Grund auf neu, um Metropolis-Hastings zu verstehen.
Von Grund auf neu
Generieren eines Angebots
Lassen Sie uns zunächst verstehen, was Metropolis-Hastings tut. Weiter oben in diesem Artikel haben wir gesagt: „Metropolis-Hastings wählt zufällig verschiedene Stichproben aus einem Raum aus“, aber woher weiß es, welche Stichprobe ausgewählt werden soll?
Dies geschieht über die Vorschlagsverteilung. Es handelt sich um eine Normalverteilung, die um die derzeit akzeptierte Stichprobe zentriert ist, und hat eine STD von 0,5. Wo 0,5 ein Hyperparameter ist, können wir optimieren; Je höher die STD des Vorschlags, desto weiter wird von der aktuell akzeptierten Probe gesucht. Lassen Sie uns das codieren.
Da wir den Mittelwert und den Standardwert der Verteilung finden müssen, nimmt diese Funktion den aktuell akzeptierten Mittelwert und den aktuell akzeptierten Standardwert und gibt Vorschläge für beide zurück.
def get_proposal(mean_current, std_current, proposal_width = 0.5): return np.random.normal(mean_current, proposal_width), \ np.random.normal(std_current, proposal_width)Annahme/Ablehnung eines Vorschlags
Lassen Sie uns nun die Logik codieren, die den Vorschlag annimmt oder ablehnt. Es besteht aus zwei Teilen: dem Prior und der Likelihood .
Lassen Sie uns zunächst die Wahrscheinlichkeit berechnen, dass der Vorschlag von der vorherigen stammt:
def prior(mean, std, prior_mean, prior_std): return st.norm(prior_mean[0], prior_mean[1]).pdf(mean)* \ st.norm(prior_std[0], prior_std[1]).pdf(std)Es nimmt einfach den Mittelwert und den Standardwert und berechnet, wie wahrscheinlich es ist, dass dieser Mittelwert und der Standardwert aus der vorherigen Verteilung stammen, die wir definiert haben.
Bei der Berechnung der Wahrscheinlichkeit berechnen wir, wie wahrscheinlich es ist, dass die Daten, die wir gesehen haben, aus der vorgeschlagenen Verteilung stammen.
def likelihood(mean, std, data): return np.prod(st.norm(mean, std).pdf(X))Also multiplizieren wir für jeden Datenpunkt die Wahrscheinlichkeit, dass dieser Datenpunkt aus der vorgeschlagenen Verteilung stammt.
Jetzt müssen wir diese Funktionen für den aktuellen Mittelwert und std und für den vorgeschlagenen Mittelwert und std aufrufen.
prior_current = prior(mean_current, std_current, prior_mean, prior_std) likelihood_current = likelihood(mean_current, std_current, data) prior_proposal = prior(mean_proposal, std_proposal, prior_mean, prior_std) likelihood_proposal = likelihood(mean_proposal, std_proposal, data)Der ganze Code:
def accept_proposal(mean_proposal, std_proposal, mean_current, \ std_current, prior_mean, prior_std, data): def prior(mean, std, prior_mean, prior_std): return st.norm(prior_mean[0], prior_mean[1]).pdf(mean)* \ st.norm(prior_std[0], prior_std[1]).pdf(std) def likelihood(mean, std, data): return np.prod(st.norm(mean, std).pdf(X)) prior_current = prior(mean_current, std_current, prior_mean, prior_std) likelihood_current = likelihood(mean_current, std_current, data) prior_proposal = prior(mean_proposal, std_proposal, prior_mean, prior_std) likelihood_proposal = likelihood(mean_proposal, std_proposal, data) return (prior_proposal * likelihood_proposal) / (prior_current * likelihood_current)Lassen Sie uns nun die letzte Funktion erstellen, die alles zusammenbindet und die benötigten späteren Samples generiert.
Generieren des Posteriors
Jetzt rufen wir die Funktionen auf, die wir oben geschrieben haben, und erzeugen das Posterior!
def get_trace(data, samples = 5000): mean_prior = 1 std_prior = 2 mean_current = mean_prior std_current = std_prior trace = { "mean": [mean_current], "std": [std_current] } for i in tqdm(range(samples)): mean_proposal, std_proposal = get_proposal(mean_current, std_current) acceptance_prob = accept_proposal(mean_proposal, std_proposal, mean_current, \ std_current, [mean_prior, std_prior], \ [mean_prior, std_prior], data) if np.random.rand() < acceptance_prob: mean_current = mean_proposal std_current = std_proposal trace['mean'].append(mean_current) trace['std'].append(std_current) return traceRaum für Verbesserung
Log ist dein Freund!
Erinnern Sie sich a * b = antilog(log(a) + log(b)) und a / b = antilog(log(a) - log(b)).
Dies ist für uns von Vorteil, da wir es mit sehr kleinen Wahrscheinlichkeiten zu tun haben, deren Multiplikation Null ergibt, also addieren wir lieber das log prob, Problem gelöst!
Unser vorheriger Code wird also zu:
def accept_proposal(mean_proposal, std_proposal, mean_current, \ std_current, prior_mean, prior_std, data): def prior(mean, std, prior_mean, prior_std): return st.norm(prior_mean[0], prior_mean[1]).logpdf(mean)+ \ st.norm(prior_std[0], prior_std[1]).logpdf(std) def likelihood(mean, std, data): return np.sum(st.norm(mean, std).logpdf(X)) prior_current = prior(mean_current, std_current, prior_mean, prior_std) likelihood_current = likelihood(mean_current, std_current, data) prior_proposal = prior(mean_proposal, std_proposal, prior_mean, prior_std) likelihood_proposal = likelihood(mean_proposal, std_proposal, data) return (prior_proposal + likelihood_proposal) - (prior_current + likelihood_current)Da wir das Protokoll der Akzeptanzwahrscheinlichkeit zurückgeben:
if np.random.rand() < acceptance_prob:
Wird:
if math.log(np.random.rand()) < acceptance_prob:
Lassen Sie uns den neuen Code ausführen und die Ergebnisse grafisch darstellen.
_ = plt.hist(trace['std'], bins = 50, label = "std") _ = plt.hist(trace['mean'], bins = 50, label = "mean") _ = plt.legend()Wie Sie sehen können, liegt der Standardwert bei 1,2 und der Mittelwert bei 1,5. Wir haben es geschafft!
Vorwärts gehen
Inzwischen haben Sie hoffentlich verstanden, wie Metropolis-Hastings funktioniert, und Sie fragen sich vielleicht, wo Sie es verwenden können.
Nun, Bayesian Methods for Hackers ist ein ausgezeichnetes Buch, das die probabilistische Programmierung erklärt, und wenn Sie mehr über das Bayes-Theorem und seine Anwendungen erfahren möchten, ist Think Bayes ein großartiges Buch von Allen B. Downey.
Vielen Dank fürs Lesen, und ich hoffe, dieser Artikel ermutigt Sie, die erstaunliche Welt der Bayes-Statistiken zu entdecken.
