MCMC 방법: Metropolis-Hastings 및 베이지안 추론
게시 됨: 2022-03-11기본적인 정의는 생략하겠습니다. MCMC(Markov Chain Monte Carlo) 방법을 사용하면 계산할 수는 없지만 분포에서 샘플을 계산할 수 있습니다.
이것은 무엇을 의미 하는가? 뒤로 물러서서 몬테카를로 샘플링에 대해 이야기해 보겠습니다.
몬테카를로 샘플링
몬테카를로 방법이란?
"몬테카를로 방법 또는 몬테카를로 실험은 수치적 결과를 얻기 위해 반복되는 무작위 샘플링에 의존하는 광범위한 종류의 계산 알고리즘입니다." (위키피디아)
분해해 보겠습니다.
예 1: 면적 추정
아래에 제시된 모양과 같이 불규칙한 모양이 있다고 상상해 보십시오.
그리고 당신은 이 모양으로 둘러싸인 영역을 결정해야 합니다. 사용할 수 있는 방법 중 하나는 모양에 작은 정사각형을 만들고 정사각형을 세는 것입니다. 그러면 면적에 대한 매우 정확한 근사값을 얻을 수 있습니다. 그러나 그것은 어렵고 시간이 많이 걸립니다.
구출에 몬테카를로 샘플링!
먼저 모양 주위에 알려진 영역의 큰 정사각형을 그립니다(예: 50cm2). 이제 우리는 이 사각형을 "매달아" 모양에 무작위로 다트를 던지기 시작합니다.
다음으로, 우리는 직사각형의 총 다트 수와 관심 있는 모양의 다트 수를 계산합니다. 사용된 "다트"의 총 수는 100이고 그 중 22개가 모양 안에 포함되었다고 가정해 보겠습니다. 이제 면적은 다음 공식으로 계산할 수 있습니다.
모양의 면적 = 정사각형의 면적 *(모양의 다트 수) / (정사각형의 다트 수)
따라서 우리의 경우 다음과 같이 됩니다.
모양의 면적 = 50 * 22/100 = 11 cm2
"다트"의 수를 10으로 곱하면 이 근사값은 실제 답에 매우 가깝습니다.
모양의 면적 = 50 * 280/1000 = 14 cm2
이것이 몬테카를로 샘플링을 사용하여 위에서 주어진 것과 같은 복잡한 작업을 분해하는 방법입니다.
큰 수의 법칙
면적 근사는 우리가 다트를 던질수록 더 가까웠고 이것은 큰 수의 법칙 때문입니다.
“대수의 법칙은 같은 실험을 여러 번 수행한 결과를 설명하는 정리입니다. 법에 따르면 여러 번 시행한 결과의 평균은 기대값에 가까워야 하고, 시행을 거듭할수록 가까워지는 경향이 있다”고 말했다.
이것은 우리의 다음 예인 유명한 몬티 홀 문제로 이어집니다.
예 2: 몬티 홀 문제
몬티 홀 문제는 매우 유명한 두뇌 자극 문제입니다.
“문이 세 개 있는데, 하나 뒤에 차가 있고, 다른 하나에는 염소가 있습니다. 당신이 문을 선택하면 주인이 다른 문을 열고 그 뒤에 염소가 있다는 것을 보여줍니다. 그런 다음 그는 결정을 변경할 것인지 묻습니다. 당신은? 왜요? 왜 안 돼?"
당신의 마음에 오는 첫 번째 것은 당신이 바꾸든 안 바꾸든 승리의 기회는 평등하다는 것입니다. 그러나 그것은 사실이 아닙니다. 동일한 것을 보여주기 위해 간단한 순서도를 만들어 보겠습니다.
차가 3번 문 뒤에 있다고 가정:
따라서 전환하면 ⅔번 이기고 전환하지 않으면 ⅓번만 이깁니다.
샘플링을 사용하여 이 문제를 해결해 보겠습니다.
wins = [] for i in range(int(10e6)): car_door = assign_car_door() choice = random.randint(0, 2) opened_door = assign_door_to_open(car_door) did_he_win = win_or_lose(choice, car_door, opened_door, switch = False) wins.append(did_he_win) print(sum(wins)/len(wins)) assign_car_door() 함수는 자동차가 있는 문 0, 1 또는 2를 선택하는 난수 생성기일 뿐입니다. assign_door_to_open 을 사용하면 뒤에 염소가 있고 선택한 문과 다른 문을 선택하고 호스트가 문을 엽니다. win_or_lose 는 true 또는 false 를 반환하여 차를 얻었는지 여부를 나타내며 문을 바꿨는지 여부를 나타내는 bool "switch"가 필요합니다.
이 시뮬레이션을 천만 번 실행해 보겠습니다.
- 전환하지 않을 경우 이길 확률: 0.334134
- 전환할 경우 승리 확률: 0.667255
이것은 순서도가 우리에게 준 답변에 매우 가깝습니다.
사실, 이 시뮬레이션을 더 많이 실행할수록 답이 실제 값에 더 가까워지므로 큰 수의 법칙이 검증됩니다.
이 표에서도 마찬가지입니다.
| 시뮬레이션 실행 | 전환하면 이길 확률 | 전환하지 않을 경우 당첨 확률 |
| 10 | 0.6 | 0.2 |
| 10^2 | 0.63 | 0.33 |
| 10^3 | 0.661 | 0.333 |
| 10^4 | 0.6683 | 0.3236 |
| 10^5 | 0.66762 | 0.33171 |
| 10^6 | 0.667255 | 0.334134 |
| 10^7 | 0.6668756 | 0.3332821 |
베이지안 사고 방식
"보다 고전적인 통계 버전으로 알려진 빈도주의자는 확률이 사건의 장기적 빈도라고 가정합니다(따라서 수여된 제목)."
“베이지안 통계는 확률이 사건에 대한 믿음의 정도를 나타내는 확률에 대한 베이지안 해석을 기반으로 하는 통계 분야의 이론입니다. 믿음의 정도는 이전 실험의 결과와 같은 사건에 대한 사전 지식이나 사건에 대한 개인적인 신념을 기반으로 할 수 있습니다.” - 해커를 위한 확률적 프로그래밍 및 베이지안 방법에서
이것은 무엇을 의미 하는가?
빈도주의적 사고 방식에서 우리는 장기적으로 확률을 봅니다. 빈도주의자가 교통사고가 일어날 확률이 0.001%라고 말할 때, 그것은 우리가 무한한 자동차 여행을 고려한다면 그 중 0.001%가 충돌로 끝난다는 것을 의미합니다.
베이지안 사고 방식은 이전의 믿음으로 시작하기 때문에 다릅니다. 0에 대한 믿음에 대해 이야기하는 경우 해당 이벤트가 절대 발생하지 않을 것이라는 귀하의 믿음을 의미합니다. 반대로, 1의 믿음은 그것이 일어날 것이라는 확신을 의미합니다.
그런 다음 데이터 관찰을 시작하면 데이터를 고려하도록 이 믿음을 업데이트합니다. 어떻게 합니까? Bayes 정리를 사용하여.
베이즈 정리
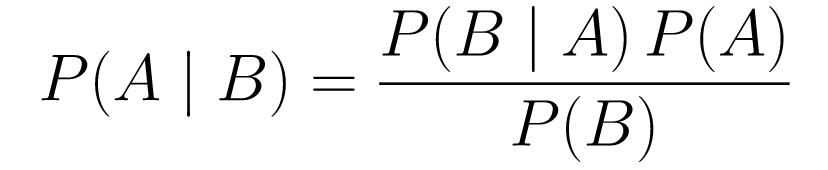 ....(1)
....(1)분해해 봅시다.
-
P(A | B)는 이벤트 B가 주어졌을 때 이벤트 A의 확률을 제공합니다. 이것은 사후, B는 우리가 관찰한 데이터입니다. 따라서 우리는 본질적으로 우리가 관찰한 데이터를 고려하여 이벤트가 발생할 확률이 무엇인지 말하는 것입니다. -
P(A)는 사전, 사건 A가 일어날 것이라는 우리의 믿음입니다. -
P(B | A)는 우도, A가 참일 때 데이터를 관찰할 확률입니다.
예를 들어 암 선별 검사를 살펴보겠습니다.
암의 확률
환자가 유방 조영술을 받으러 갔다가 유방 조영술에서 양성으로 나왔다고 가정해 보겠습니다. 환자가 실제로 암에 걸릴 확률은 얼마입니까?
확률을 정의해 보겠습니다.
- 여성의 1%가 유방암에 걸립니다.
- 유방 조영술은 실제로 존재하는 경우의 80%에서 암을 감지합니다.
- 유방 조영술의 9.6%는 실제로 암에 걸리지 않았는데 암이 있다고 잘못 보고합니다.
따라서 유방 조영술에서 양성 반응이 나왔다면 암에 걸릴 확률이 80%라면 그것은 잘못된 것입니다. 암에 걸리는 것은 드문 경우, 즉 여성의 1%만이 유방암에 걸린다는 점을 고려하지 않을 것입니다. 우리는 이것을 이전처럼 받아들일 필요가 있으며, 이것이 Bayes 정리가 작용하는 곳입니다.
P(C+ | T+) =(P(T+|C+)*P(C+))/P(T+)
-
P(C+ | T+): 검사가 양성인 경우 암이 있을 확률입니다. 이것이 우리가 관심을 갖는 것입니다. -
P(T+ | C+): 이것은 암이 있다고 가정할 때 검사가 양성일 확률입니다. 위에서 논의한 바와 같이 이것은 80% = 0.8과 같습니다. -
P(C+): 이것은 사전 확률, 개인이 암에 걸릴 확률이며 1% = 0.01과 같습니다. -
P(T+): 이것은 테스트가 무엇이든 상관없이 양성일 확률이므로 P(T+) = P(T+|C-) P(C-)+P(T+|C+) P (C+) -
P(T+ | C-): 검사에서 양성으로 나왔지만 암이 없을 확률로 0.096으로 주어진다. -
P(C-): 암에 걸릴 확률이 1%이므로 암에 걸리지 않을 확률은 99% = 0.99입니다. -
P(T+ | C+): 이것은 당신이 암에 걸렸다는 것을 감안할 때 검사가 양성으로 돌아올 확률입니다. 이것은 80% = 0.8과 같습니다. -
P(C+): 암에 걸릴 확률은 1% = 0.01입니다.
이 모든 것을 원래 공식에 대입하면 다음과 같습니다.
따라서 유방 X선 촬영에서 양성으로 나왔을 때 암에 걸릴 확률은 7.76%입니다. 처음에는 이상하게 보일 수 있지만 의미가 있습니다. 테스트는 시간의 9.6%(상당히 높음)의 위양성을 나타내므로 주어진 모집단에서 많은 위양성이 있을 것입니다. 희귀질환의 경우 대부분의 양성 검사 결과가 틀릴 것입니다.
이제 몬티홀 문제를 다시 살펴보고 베이즈 정리를 사용하여 해결해 보겠습니다.
몬티 홀 문제
사전은 다음과 같이 정의할 수 있습니다.
- 처음에 A 문을 선택했다고 가정합니다.
- P(H) = ⅓, ⅓ ⅓ 세 개의 문 모두에 대해, 즉 문이 열리고 염소가 나타나기 전에 차가 그 뒤에 있을 확률은 동일했습니다.
가능성은 다음과 같이 정의할 수 있습니다.
-
P(D|H), 여기서 사건 D는 Monty가 문 B를 선택하고 그 뒤에 차가 없는 것입니다. - 차가 A문 뒤에 있다면
P(D|H)= 1/2 - 자동차가 B문을 선택할 확률이 50%이고 C문을 선택할 확률이 50%이기 때문입니다. - 차가 B 문 뒤에 있으면
P(D|H)= 0입니다. 차가 뒤에 있으면 B 문을 선택할 확률이 0%이기 때문입니다. -
P(D|H)= 1 차가 C 뒤에 있고 A를 선택하면 그가 문 B를 선택할 확률이 100%입니다.
우리는 P(H|D) 에 관심이 있습니다. P(H|D) 는 다른 문 중 하나 뒤에 염소가 있는 것을 볼 때 차가 문 뒤에 있을 확률입니다.

사후 P(H|D) 에서 A에서 문 C로 전환하면 승리 확률이 증가함을 알 수 있습니다.
메트로폴리스-헤이스팅스
이제 지금까지 다룬 모든 내용을 결합하고 Metropolis-Hastings가 작동하는 방식을 이해하려고 합니다.
Metropolis-Hastings는 Bayes 정리를 사용하여 직접 샘플링하기 어려운 복잡한 분포의 사후 분포를 얻습니다.
어떻게? 기본적으로 방정식(1)에서 확률 비율 P(B)를 보고 있기 때문에 공간에서 다른 샘플을 무작위로 선택하고 새 샘플이 마지막 샘플보다 사후에 나올 가능성이 더 높은지 확인합니다. 취소됨:
P(acceptance) = ( P(newSample) * 새 샘플의 가능성) / (P(oldSample) * 이전 샘플의 가능성)
각각의 새로운 샘플의 "가능성"은 함수 f 에 의해 결정됩니다. 이것이 f 가 샘플링하려는 사후값에 비례해야 하는 이유입니다.
θ'가 승인 또는 거부되는지 결정하려면 각각의 새로 제안된 θ'에 대해 다음 비율을 계산해야 합니다.
여기서 θ는 이전 샘플이고 P(D| θ) 는 샘플 θ의 가능성입니다.
이것을 더 잘 이해하기 위해 예를 들어보겠습니다. 데이터가 있지만 데이터에 맞는 정규 분포를 찾고자 한다고 가정해 보겠습니다.
X ~ N(평균, 표준)
이제 평균과 표준에 대한 사전 정의를 정의해야 합니다. 단순화를 위해 둘 다 평균이 1이고 표준이 2인 정규 분포를 따른다고 가정합니다.
평균 ~ N(1, 2)
표준 ~ N(1, 2)
이제 일부 데이터를 생성하고 실제 평균과 표준이 각각 0.5와 1.2라고 가정하겠습니다.
import numpy as np import matplotlib.pyplot as plt import scipy.stats as st meanX = 1.5 stdX = 1.2 X = np.random.normal(meanX, stdX, size = 1000) _ = plt.hist(X, bins = 50)파이MC3
먼저 PyMC3 이라는 라이브러리를 사용하여 데이터를 모델링하고 평균 및 표준에 대한 사후 분포를 찾습니다.
import pymc3 as pm with pm.Model() as model: mean = pm.Normal("mean", mu = 1, sigma = 2) std = pm.Normal("std", mu = 1, sigma = 2) x = pm.Normal("X", mu = mean, sigma = std, observed = X) step = pm.Metropolis() trace = pm.sample(5000, step = step)코드를 살펴보겠습니다.
먼저 평균과 표준에 대한 사전 정의, 즉 평균이 1이고 표준이 2인 법선을 정의합니다.
x = pm.Normal("X", mu = 평균, 시그마 = 표준, 관측값 = X)
이 줄에서 관심 있는 변수를 정의합니다. 이전에 정의한 평균과 표준을 사용하며 이전에 계산한 관찰된 값도 사용합니다.
결과를 살펴보겠습니다.
_ = plt.hist(trace['std'], bins = 50, label = "std") _ = plt.hist(trace['mean'], bins = 50, label = "mean") _ = plt.legend()std는 1.2를 중심으로 하고 평균은 1.55에 있습니다. 아주 가깝습니다!
이제 Metropolis-Hastings를 이해하기 위해 처음부터 시작해 보겠습니다.
기스로부터
제안 생성
먼저 Metropolis-Hastings가 하는 일을 이해합시다. 이 기사 앞부분에서 "Metropolis-Hastings는 공간에서 다른 샘플을 무작위로 선택합니다."라고 말했지만 어떤 샘플을 선택해야 하는지 어떻게 압니까?
제안 배포를 사용하여 그렇게 합니다. 현재 수용된 표본을 중심으로 하는 정규 분포이며 STD가 0.5입니다. 0.5가 초매개변수인 경우 조정할 수 있습니다. 제안서의 STD가 많을수록 현재 승인된 샘플에서 더 많이 검색합니다. 이것을 코딩해 봅시다.
분포의 평균과 표준을 찾아야 하므로 이 함수는 현재 허용되는 평균과 현재 허용되는 표준을 취하고 둘 다에 대한 제안을 반환합니다.
def get_proposal(mean_current, std_current, proposal_width = 0.5): return np.random.normal(mean_current, proposal_width), \ np.random.normal(std_current, proposal_width)제안 수락/거절
이제 제안을 수락하거나 거부하는 논리를 코딩해 보겠습니다. 사전 및 가능성 의 두 부분으로 구성됩니다.
먼저 이전 제안에서 나올 확률을 계산해 보겠습니다.
def prior(mean, std, prior_mean, prior_std): return st.norm(prior_mean[0], prior_mean[1]).pdf(mean)* \ st.norm(prior_std[0], prior_std[1]).pdf(std)그것은 평균과 표준을 취하고 이 평균 과 표준 이 우리가 정의한 이전 분포 에서 나올 가능성을 계산합니다.
가능성을 계산할 때 우리가 본 데이터가 제안된 분포에서 나올 가능성을 계산합니다.
def likelihood(mean, std, data): return np.prod(st.norm(mean, std).pdf(X))따라서 각 데이터 포인트에 대해 제안된 분포에서 해당 데이터 포인트가 나올 확률을 곱합니다.
이제 현재 평균 및 std 및 제안된 평균 및 std 에 대해 이러한 함수를 호출해야 합니다.
prior_current = prior(mean_current, std_current, prior_mean, prior_std) likelihood_current = likelihood(mean_current, std_current, data) prior_proposal = prior(mean_proposal, std_proposal, prior_mean, prior_std) likelihood_proposal = likelihood(mean_proposal, std_proposal, data)전체 코드:
def accept_proposal(mean_proposal, std_proposal, mean_current, \ std_current, prior_mean, prior_std, data): def prior(mean, std, prior_mean, prior_std): return st.norm(prior_mean[0], prior_mean[1]).pdf(mean)* \ st.norm(prior_std[0], prior_std[1]).pdf(std) def likelihood(mean, std, data): return np.prod(st.norm(mean, std).pdf(X)) prior_current = prior(mean_current, std_current, prior_mean, prior_std) likelihood_current = likelihood(mean_current, std_current, data) prior_proposal = prior(mean_proposal, std_proposal, prior_mean, prior_std) likelihood_proposal = likelihood(mean_proposal, std_proposal, data) return (prior_proposal * likelihood_proposal) / (prior_current * likelihood_current)이제 모든 것을 연결하고 필요한 사후 샘플을 생성하는 최종 함수를 생성해 보겠습니다.
사후 생성
이제 위에서 작성한 함수를 호출하고 사후를 생성합니다!
def get_trace(data, samples = 5000): mean_prior = 1 std_prior = 2 mean_current = mean_prior std_current = std_prior trace = { "mean": [mean_current], "std": [std_current] } for i in tqdm(range(samples)): mean_proposal, std_proposal = get_proposal(mean_current, std_current) acceptance_prob = accept_proposal(mean_proposal, std_proposal, mean_current, \ std_current, [mean_prior, std_prior], \ [mean_prior, std_prior], data) if np.random.rand() < acceptance_prob: mean_current = mean_proposal std_current = std_proposal trace['mean'].append(mean_current) trace['std'].append(std_current) return trace개선의 여지
로그는 당신의 친구입니다!
a * b = antilog(log(a) + log(b)) 및 a / b = antilog(log(a) - log(b)).
이것은 우리가 매우 작은 확률을 처리하고 곱하면 0이 될 것이기 때문에 우리에게 유리합니다. 그래서 우리는 문제가 해결된 로그 확률을 추가할 것입니다!
따라서 이전 코드는 다음과 같습니다.
def accept_proposal(mean_proposal, std_proposal, mean_current, \ std_current, prior_mean, prior_std, data): def prior(mean, std, prior_mean, prior_std): return st.norm(prior_mean[0], prior_mean[1]).logpdf(mean)+ \ st.norm(prior_std[0], prior_std[1]).logpdf(std) def likelihood(mean, std, data): return np.sum(st.norm(mean, std).logpdf(X)) prior_current = prior(mean_current, std_current, prior_mean, prior_std) likelihood_current = likelihood(mean_current, std_current, data) prior_proposal = prior(mean_proposal, std_proposal, prior_mean, prior_std) likelihood_proposal = likelihood(mean_proposal, std_proposal, data) return (prior_proposal + likelihood_proposal) - (prior_current + likelihood_current)합격 확률의 로그를 반환하기 때문에:
if np.random.rand() < acceptance_prob:
다음이 됩니다.
if math.log(np.random.rand()) < acceptance_prob:
새 코드를 실행하고 결과를 플로팅해 보겠습니다.
_ = plt.hist(trace['std'], bins = 50, label = "std") _ = plt.hist(trace['mean'], bins = 50, label = "mean") _ = plt.legend()보시다시피 std 는 1.2의 중심에 있고 평균 은 1.5에 있습니다. 우리는 해냈다!
앞으로 나아가 다
지금쯤이면 Metropolis-Hastings가 어떻게 작동하는지 이해하고 어디에 사용할 수 있는지 궁금할 것입니다.
글쎄요, Bayesian Methods for Hackers 는 확률 프로그래밍을 설명하는 훌륭한 책입니다. Bayes 정리와 그 적용에 대해 더 알고 싶다면 Allen B. Downey의 Think Bayes 가 훌륭한 책입니다.
읽어주셔서 감사합니다. 이 기사가 베이지안 통계의 놀라운 세계를 발견하는 데 도움이 되기를 바랍니다.
