Metodi MCMC: Metropolis-Hastings e inferenza bayesiana
Pubblicato: 2022-03-11Togliamo di mezzo la definizione di base: i metodi Markov Chain Monte Carlo (MCMC) ci consentono di calcolare campioni da una distribuzione anche se non possiamo calcolarla.
Cosa significa questo? Torniamo indietro e parliamo del campionamento Monte Carlo.
Campionamento Montecarlo
Quali sono i metodi Monte Carlo?
"I metodi Monte Carlo, o esperimenti Monte Carlo, sono un'ampia classe di algoritmi computazionali che si basano su campionamenti casuali ripetuti per ottenere risultati numerici". (Wikipedia)
Analizziamolo.
Esempio 1: Stima dell'area
Immagina di avere una forma irregolare, come la forma presentata di seguito:
E tu hai il compito di determinare l'area racchiusa da questa forma. Uno dei metodi che puoi usare è creare piccoli quadrati nella forma, contare i quadrati e questo ti darà un'approssimazione abbastanza accurata dell'area. Tuttavia, è difficile e richiede tempo.
Campionamento Monte Carlo in soccorso!
Per prima cosa, disegniamo un grande quadrato di un'area nota attorno alla forma, ad esempio di 50 cm2. Ora "appendiamo" questo quadrato e iniziamo a lanciare freccette casualmente sulla forma.
Successivamente, contiamo il numero totale di freccette nel rettangolo e il numero di freccette nella forma che ci interessa. Supponiamo che il numero totale di “freccette” utilizzate sia 100 e che 22 di esse siano finite all'interno della forma. Ora l'area può essere calcolata con la semplice formula:
area della forma = area del quadrato *(numero di freccette nella forma) / (numero di freccette nel quadrato)
Quindi, nel nostro caso, questo si riduce a:
area di forma = 50 * 22/100 = 11 cm2
Se moltiplichiamo il numero di "freccette" per un fattore 10, questa approssimazione diventa molto vicina alla risposta reale:
area di forma = 50 * 280/1000 = 14 cm2
Questo è il modo in cui analizziamo le attività complicate, come quella data sopra, utilizzando il campionamento Monte Carlo.
La legge dei grandi numeri
L'approssimazione dell'area era più vicina quanto più dardi lanciavamo, e questo è dovuto alla Legge dei Grandi Numeri:
“La legge dei grandi numeri è un teorema che descrive il risultato dell'esecuzione dello stesso esperimento un gran numero di volte. Secondo la legge, la media dei risultati ottenuti da un gran numero di prove dovrebbe essere vicina al valore atteso e tenderà ad avvicinarsi man mano che vengono eseguite più prove".
Questo ci porta al nostro prossimo esempio, il famoso problema di Monty Hall.
Esempio 2: Il problema di Monty Hall
Il problema di Monty Hall è un rompicapo molto famoso:
“Ci sono tre porte, una ha una macchina dietro, le altre hanno una capra dietro. Scegli una porta, l'host apre un'altra porta e ti mostra che c'è una capra dietro di essa. Poi ti chiede se vuoi cambiare la tua decisione. Fai? Come mai? Perché no?"
La prima cosa che ti viene in mente è che le possibilità di vincita sono uguali indipendentemente dal fatto che cambi o meno, ma non è vero. Facciamo un semplice diagramma di flusso per dimostrare lo stesso.
Supponendo che l'auto sia dietro la porta 3:
Quindi, se cambi, vinci ⅔ volte, e se non cambi, vinci solo ⅓ volte.
Risolviamolo usando il campionamento.
wins = [] for i in range(int(10e6)): car_door = assign_car_door() choice = random.randint(0, 2) opened_door = assign_door_to_open(car_door) did_he_win = win_or_lose(choice, car_door, opened_door, switch = False) wins.append(did_he_win) print(sum(wins)/len(wins)) La funzione assign_car_door() è solo un generatore di numeri casuali che seleziona una porta 0, 1 o 2, dietro la quale c'è un'auto. Usando assign_door_to_open seleziona una porta che ha una capra dietro e non è quella che hai selezionato, e l'host la apre. win_or_lose restituisce true o false , indicando se hai vinto l'auto o meno, ci vuole un bool "interruttore" che dice se hai cambiato la porta o meno.
Eseguiamo questa simulazione 10 milioni di volte:
- Probabilità di vincita se non si cambia: 0,334134
- Probabilità di vincita in caso di cambio: 0,667255
Questo è molto vicino alle risposte che ci ha dato il diagramma di flusso.
In effetti, più eseguiamo questa simulazione, più la risposta si avvicina al valore vero, convalidando quindi la legge dei numeri grandi:
Lo stesso si può vedere da questa tabella:
| Le simulazioni vengono eseguite | Probabilità di vincita in caso di cambio | Probabilità di vincita se non cambi |
| 10 | 0.6 | 0.2 |
| 10^2 | 0,63 | 0,33 |
| 10^3 | 0,661 | 0,333 |
| 10^4 | 0,6683 | 0,3236 |
| 10^5 | 0,66762 | 0,33171 |
| 10^6 | 0,667255 | 0.334134 |
| 10^7 | 0.6668756 | 0.3332821 |
Il modo di pensare bayesiano
"Frequentist, noto come la versione più classica della statistica, presuppone che la probabilità sia la frequenza a lungo termine degli eventi (da cui il titolo conferito)."
“La statistica bayesiana è una teoria nel campo della statistica basata sull'interpretazione bayesiana della probabilità in cui la probabilità esprime un grado di credenza in un evento. Il grado di convinzione può essere basato su una conoscenza preliminare dell'evento, come i risultati di esperimenti precedenti, o su convinzioni personali sull'evento". - da Programmazione probabilistica e Metodi bayesiani per hacker
Cosa significa questo?
Nel modo di pensare frequentista, guardiamo alle probabilità a lungo termine. Quando un frequentista dice che c'è una probabilità dello 0,001% che si verifichi un incidente d'auto, significa che, se consideriamo infiniti viaggi in macchina, lo 0,001% di questi finirà con un incidente.
Una mentalità bayesiana è diversa, poiché iniziamo con un precedente, una convinzione. Se parliamo di una convinzione pari a 0, significa che la tua convinzione è che l'evento non accadrà mai; al contrario, una convinzione di 1 significa che sei sicuro che accadrà.
Quindi, una volta che iniziamo a osservare i dati, aggiorniamo questa convinzione per prendere in considerazione i dati. Come facciamo questo? Usando il teorema di Bayes.
Teorema di Bayes
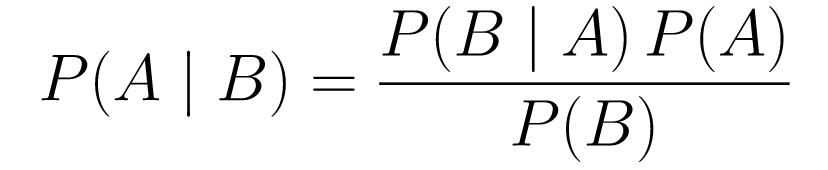 ....(1)
....(1)Analizziamolo.
-
P(A | B)ci dà la probabilità dell'evento A dato l'evento B. Questo è il posteriore, B è il dato che abbiamo osservato, quindi stiamo essenzialmente dicendo qual è la probabilità che un evento accada, considerando i dati che abbiamo osservato. -
P(A)è il priore, la nostra convinzione che l'evento A accadrà. -
P(B | A)è la verosimiglianza, qual è la probabilità che osserveremo i dati dato che A è vero.
Diamo un'occhiata a un esempio, il test di screening del cancro.
Probabilità di cancro
Diciamo che un paziente va a fare una mammografia e la mammografia torna positiva. Qual è la probabilità che il paziente abbia effettivamente il cancro?
Definiamo le probabilità:
- L'1% delle donne ha il cancro al seno.
- Le mammografie rilevano il cancro l'80% delle volte quando è effettivamente presente.
- Il 9,6% delle mammografie dichiara erroneamente di avere il cancro quando in realtà non ce l'hai.
Quindi, se dovessi dire che se una mammografia è risultata positiva, significa che c'è l'80% di possibilità che tu abbia il cancro, sarebbe sbagliato. Non prenderesti in considerazione che avere il cancro è un evento raro, cioè che solo l'1% delle donne ha il cancro al seno. Dobbiamo prendere questo come precedente, ed è qui che entra in gioco il teorema di Bayes:
P(C+ | T+) =(P(T+|C+)*P(C+))/P(T+)
-
P(C+ | T+): Questa è la probabilità che ci sia il cancro, dato che il test è positivo, questo è ciò che ci interessa. -
P(T+ | C+): Questa è la probabilità che il test sia positivo, dato che c'è il cancro, questo, come discusso sopra è pari a 80% = 0,8. -
P(C+): Questa è la probabilità a priori, la probabilità che un individuo abbia il cancro, che è pari a 1% = 0,01. -
P(T+): Questa è la probabilità che il test sia positivo, qualunque cosa accada, quindi ha due componenti: P(T+) = P(T+|C-) P(C-)+P(T+|C+) P (C+) -
P(T+ | C-): Questa è la probabilità che il test sia risultato positivo ma non ci sia cancro, è data da 0,096. -
P(C-): Questa è la probabilità di non avere il cancro poiché la probabilità di avere il cancro è dell'1%, questo è pari a 99% = 0,99. -
P(T+ | C+): Questa è la probabilità che il test sia risultato positivo, dato che hai il cancro, è pari a 80% = 0,8. -
P(C+): Questa è la probabilità di avere il cancro, che è pari a 1% = 0,01.
Inserendo tutto questo nella formula originale:
Quindi, dato che la mammografia è risultata positiva, c'è una probabilità del 7,76% che il paziente abbia il cancro. All'inizio potrebbe sembrare strano, ma ha senso. Il test fornisce un falso positivo il 9,6% delle volte (abbastanza alto), quindi ci saranno molti falsi positivi in una data popolazione. Per una malattia rara, la maggior parte dei risultati positivi del test sarà errata.
Rivisitiamo ora il problema di Monty Hall e risolviamolo usando il teorema di Bayes.

Problema Monty Hall
I priori possono essere definiti come:
- Supponiamo di scegliere la porta A come scelta all'inizio.
- P(H) = ⅓, ⅓. ⅓ per tutte e tre le porte, il che significa che prima che la porta fosse aperta e la capra si fosse rivelata, c'era la stessa possibilità che l'auto fosse dietro a ognuna di esse.
La probabilità può essere definita come:
-
P(D|H), dove l'evento D è che Monty sceglie la porta B e non c'è macchina dietro di essa. -
P(D|H)= 1/2 se l'auto è dietro la porta A - poiché c'è una probabilità del 50% che scelga la porta B e del 50% che scelga la porta C. -
P(D|H)= 0 se l'auto è dietro la porta B, poiché c'è una probabilità dello 0% che scelga la porta B se l'auto è dietro di essa. -
P(D|H)= 1 se l'auto è dietro C e tu scegli A, c'è una probabilità del 100% che scelga la porta B.
Siamo interessati a P(H|D) , che è la probabilità che l'auto sia dietro una porta dato che ci mostra una capra dietro una delle altre porte.
Si può vedere dal posteriore, P(H|D) , che il passaggio alla porta C da A aumenterà le probabilità di vincita.
Metropolis-Hastings
Ora, uniamo tutto ciò che abbiamo trattato finora e cerchiamo di capire come funziona Metropolis-Hastings.
Metropolis-Hastings usa il teorema di Bayes per ottenere la distribuzione a posteriori di una distribuzione complessa, dalla quale il campionamento diretto è difficile.
Come? In sostanza, seleziona casualmente diversi campioni da uno spazio e controlla se è più probabile che il nuovo campione provenga dal posteriore rispetto all'ultimo campione, poiché stiamo osservando il rapporto di probabilità, P(B) nell'equazione (1), ottiene cancellato:
P(accettazione) = ( P(nuovoCampione) * Probabilità di un nuovo campione) / (P(vecchioCampione) * Probabilità di un vecchio campione)
La “probabilità” di ogni nuovo campione è determinata dalla funzione f . Ecco perché f deve essere proporzionale al posteriore da cui vogliamo campionare.
Per decidere se θ′ deve essere accettato o rifiutato, è necessario calcolare il seguente rapporto per ogni nuova proposta θ':
Dove θ è il vecchio campione, P(D| θ) è la probabilità del campione θ.
Usiamo un esempio per capirlo meglio. Diciamo che hai dei dati ma vuoi scoprire la distribuzione normale adatta, quindi:
X ~ N(media, std)
Ora dobbiamo definire i priori per la media e per std entrambi. Per semplicità, assumiamo che entrambi seguano una distribuzione normale con media 1 e std 2:
Media ~ N(1, 2)
std ~ N(1, 2)
Ora, generiamo alcuni dati e assumiamo che la vera media e std siano rispettivamente 0,5 e 1,2.
import numpy as np import matplotlib.pyplot as plt import scipy.stats as st meanX = 1.5 stdX = 1.2 X = np.random.normal(meanX, stdX, size = 1000) _ = plt.hist(X, bins = 50)PyMC3
Usiamo prima una libreria chiamata PyMC3 per modellare i dati e trovare la distribuzione a posteriori per la media e std.
import pymc3 as pm with pm.Model() as model: mean = pm.Normal("mean", mu = 1, sigma = 2) std = pm.Normal("std", mu = 1, sigma = 2) x = pm.Normal("X", mu = mean, sigma = std, observed = X) step = pm.Metropolis() trace = pm.sample(5000, step = step)Esaminiamo il codice.
Innanzitutto, definiamo il prior per media e std, cioè una normale con media 1 e std 2.
x = pm.Normal(“X”, mu = media, sigma = std, osservato = X)
In questa riga definiamo la variabile che ci interessa; prende la media e lo std che abbiamo definito in precedenza, prende anche i valori osservati che abbiamo calcolato in precedenza.
Diamo un'occhiata ai risultati:
_ = plt.hist(trace['std'], bins = 50, label = "std") _ = plt.hist(trace['mean'], bins = 50, label = "mean") _ = plt.legend()Lo std è centrato intorno a 1,2 e la media è a 1,55 - abbastanza vicino!
Ora facciamolo da zero per capire Metropolis-Hastings.
Da zero
Generazione di una proposta
Per prima cosa, capiamo cosa fa Metropolis-Hastings. In precedenza in questo articolo, abbiamo detto: "Metropolis-Hastings seleziona casualmente campioni diversi da uno spazio", ma come fa a sapere quale campione selezionare?
Lo fa utilizzando la distribuzione della proposta. È una distribuzione normale centrata sul campione attualmente accettato e ha un STD di 0,5. Dove 0.5 è un iperparametro, possiamo modificare; quanto più è lo STD della proposta, tanto più cercherà dal campione attualmente accettato. Codifichiamo questo.
Poiché dobbiamo trovare la media e lo std della distribuzione, questa funzione prenderà la media attualmente accettata e lo std attualmente accettato e restituirà proposte per entrambi.
def get_proposal(mean_current, std_current, proposal_width = 0.5): return np.random.normal(mean_current, proposal_width), \ np.random.normal(std_current, proposal_width)Accettazione/Rifiuto di una proposta
Ora, codifichiamo la logica che accetta o rifiuta la proposta. Si compone di due parti: il priore e la verosimiglianza .
Per prima cosa, calcoliamo la probabilità che la proposta provenga dal precedente:
def prior(mean, std, prior_mean, prior_std): return st.norm(prior_mean[0], prior_mean[1]).pdf(mean)* \ st.norm(prior_std[0], prior_std[1]).pdf(std)Prende solo la media e lo std e calcola quanto è probabile che questa media e lo std provengano dalla distribuzione precedente che abbiamo definito.
Nel calcolare la probabilità, calcoliamo quanto è probabile che i dati che abbiamo visto provengano dalla distribuzione proposta.
def likelihood(mean, std, data): return np.prod(st.norm(mean, std).pdf(X))Quindi, per ogni punto dati, moltiplichiamo la probabilità che quel punto dati provenga dalla distribuzione proposta.
Ora, dobbiamo chiamare queste funzioni per la media e std correnti e per la media e std proposte.
prior_current = prior(mean_current, std_current, prior_mean, prior_std) likelihood_current = likelihood(mean_current, std_current, data) prior_proposal = prior(mean_proposal, std_proposal, prior_mean, prior_std) likelihood_proposal = likelihood(mean_proposal, std_proposal, data)L'intero codice:
def accept_proposal(mean_proposal, std_proposal, mean_current, \ std_current, prior_mean, prior_std, data): def prior(mean, std, prior_mean, prior_std): return st.norm(prior_mean[0], prior_mean[1]).pdf(mean)* \ st.norm(prior_std[0], prior_std[1]).pdf(std) def likelihood(mean, std, data): return np.prod(st.norm(mean, std).pdf(X)) prior_current = prior(mean_current, std_current, prior_mean, prior_std) likelihood_current = likelihood(mean_current, std_current, data) prior_proposal = prior(mean_proposal, std_proposal, prior_mean, prior_std) likelihood_proposal = likelihood(mean_proposal, std_proposal, data) return (prior_proposal * likelihood_proposal) / (prior_current * likelihood_current)Ora creiamo la funzione finale che legherà tutto insieme e genererà i campioni posteriori di cui abbiamo bisogno.
Generazione del posteriore
Ora chiamiamo le funzioni che abbiamo scritto sopra e generiamo il posteriore!
def get_trace(data, samples = 5000): mean_prior = 1 std_prior = 2 mean_current = mean_prior std_current = std_prior trace = { "mean": [mean_current], "std": [std_current] } for i in tqdm(range(samples)): mean_proposal, std_proposal = get_proposal(mean_current, std_current) acceptance_prob = accept_proposal(mean_proposal, std_proposal, mean_current, \ std_current, [mean_prior, std_prior], \ [mean_prior, std_prior], data) if np.random.rand() < acceptance_prob: mean_current = mean_proposal std_current = std_proposal trace['mean'].append(mean_current) trace['std'].append(std_current) return traceMargini di miglioramento
Log è tuo amico!
Richiama a * b = antilog(log(a) + log(b)) e a / b = antilog(log(a) - log(b)).
Questo è vantaggioso per noi perché avremo a che fare con probabilità molto piccole, moltiplicando che risulterà in zero, quindi aggiungeremo piuttosto il log prob, problema risolto!
Quindi, il nostro codice precedente diventa:
def accept_proposal(mean_proposal, std_proposal, mean_current, \ std_current, prior_mean, prior_std, data): def prior(mean, std, prior_mean, prior_std): return st.norm(prior_mean[0], prior_mean[1]).logpdf(mean)+ \ st.norm(prior_std[0], prior_std[1]).logpdf(std) def likelihood(mean, std, data): return np.sum(st.norm(mean, std).logpdf(X)) prior_current = prior(mean_current, std_current, prior_mean, prior_std) likelihood_current = likelihood(mean_current, std_current, data) prior_proposal = prior(mean_proposal, std_proposal, prior_mean, prior_std) likelihood_proposal = likelihood(mean_proposal, std_proposal, data) return (prior_proposal + likelihood_proposal) - (prior_current + likelihood_current)Poiché stiamo restituendo il log della probabilità di accettazione:
if np.random.rand() < acceptance_prob:
diventa:
if math.log(np.random.rand()) < acceptance_prob:
Eseguiamo il nuovo codice e tracciamo i risultati.
_ = plt.hist(trace['std'], bins = 50, label = "std") _ = plt.hist(trace['mean'], bins = 50, label = "mean") _ = plt.legend()Come puoi vedere, lo std è centrato a 1,2 e la media a 1,5. Ce l'abbiamo fatta!
Andando avanti
A questo punto, si spera che tu abbia capito come funziona Metropolis-Hastings e potresti chiederti dove puoi usarlo.
Bene, Bayesian Methods for Hackers è un libro eccellente che spiega la programmazione probabilistica, e se vuoi saperne di più sul teorema di Bayes e sulle sue applicazioni, Think Bayes è un ottimo libro di Allen B. Downey.
Grazie per aver letto e spero che questo articolo ti incoraggi a scoprire il fantastico mondo delle statistiche bayesiane.
