Metody MCMC: Metropolis-Hastings i wnioskowanie bayesowskie
Opublikowany: 2022-03-11Usuńmy podstawową definicję: Metody Markowa Łańcucha Monte Carlo (MCMC) pozwalają nam obliczyć próbki z dystrybucji, nawet jeśli nie możemy tego obliczyć.
Co to znaczy? Cofnijmy się i porozmawiajmy o próbkach Monte Carlo.
Próbkowanie Monte Carlo
Jakie są metody Monte Carlo?
„Metody Monte Carlo lub eksperymenty Monte Carlo to szeroka klasa algorytmów obliczeniowych, które opierają się na wielokrotnym losowym próbkowaniu w celu uzyskania wyników liczbowych”. (Wikipedia)
Rozłóżmy to.
Przykład 1: Oszacowanie powierzchni
Wyobraź sobie, że masz nieregularny kształt, taki jak przedstawiony poniżej:
A ty masz za zadanie określić obszar objęty tym kształtem. Jedną z metod, których możesz użyć, jest zrobienie małych kwadratów w kształcie, policzenie kwadratów, a to da ci dość dokładne przybliżenie obszaru. Jest to jednak trudne i czasochłonne.
Próbkowanie Monte Carlo na ratunek!
Najpierw wokół kształtu narysujemy duży kwadrat o znanej powierzchni, na przykład 50 cm2. Teraz „zawieszamy” ten kwadrat i zaczynamy losowo rzucać rzutkami w kształt.
Następnie liczymy całkowitą liczbę rzutek w prostokącie oraz liczbę rzutek w kształcie, który nas interesuje. Załóżmy, że łączna liczba użytych rzutek wyniosła 100 i że 22 z nich znalazły się w tym kształcie. Teraz obszar można obliczyć za pomocą prostego wzoru:
powierzchnia kształtu = powierzchnia kwadratu *(liczba rzutek w kształcie) / (liczba rzutek w kwadracie)
Tak więc w naszym przypadku sprowadza się to do:
powierzchnia kształtu = 50 * 22/100 = 11 cm2
Jeśli pomnożymy liczbę „rzutek” przez współczynnik 10, to przybliżenie staje się bardzo bliskie prawdziwej odpowiedzi:
powierzchnia kształtu = 50 * 280/1000 = 14 cm2
W ten sposób rozkładamy skomplikowane zadania, takie jak to podane powyżej, za pomocą próbkowania Monte Carlo.
Prawo wielkich liczb
Przybliżenie obszaru było tym bliższe, im więcej rzuciliśmy rzutkami, a to z powodu Prawa Wielkich Liczb:
„Prawo wielkich liczb to twierdzenie, które opisuje wynik przeprowadzenia tego samego eksperymentu wiele razy. Zgodnie z prawem średnia wyników uzyskanych z dużej liczby prób powinna być zbliżona do wartości oczekiwanej i będzie się zbliżać w miarę przeprowadzania większej liczby prób.”
To prowadzi nas do naszego następnego przykładu, słynnego problemu Monty Halla.
Przykład 2: Problem Monty'ego Halla
Problem Monty'ego Halla to bardzo znana łamigłówka:
„Jest troje drzwi, za jednymi stoi samochód, za innymi koza. Wybierasz drzwi, gospodarz otwiera inne drzwi i pokazuje, że za nimi stoi koza. Następnie pyta, czy chcesz zmienić swoją decyzję. Czy ty? Czemu? Dlaczego nie?"
Pierwszą rzeczą, która przychodzi ci do głowy, jest to, że szanse na wygraną są równe niezależnie od tego, czy się zmienisz, czy nie, ale to nieprawda. Zróbmy prosty schemat blokowy, aby zademonstrować to samo.
Zakładając, że samochód jest za drzwiami 3:
Dlatego jeśli się zmienisz, wygrasz ⅔ razy, a jeśli się nie zmienisz, wygrasz tylko ⅓ razy.
Rozwiążmy to za pomocą próbkowania.
wins = [] for i in range(int(10e6)): car_door = assign_car_door() choice = random.randint(0, 2) opened_door = assign_door_to_open(car_door) did_he_win = win_or_lose(choice, car_door, opened_door, switch = False) wins.append(did_he_win) print(sum(wins)/len(wins)) Funkcja assign_car_door() to po prostu generator liczb losowych, który wybiera drzwi 0, 1 lub 2, za którymi znajduje się samochód. Użycie assign_door_to_open wybiera drzwi, za którymi znajduje się koza, a nie te, które wybrałeś, a gospodarz je otwiera. win_or_lose zwraca wartość true lub false , oznaczającą, czy wygrałeś samochód, czy nie.
Przeprowadźmy tę symulację 10 milionów razy:
- Prawdopodobieństwo wygranej, jeśli się nie zmienisz: 0,334134
- Prawdopodobieństwo wygranej w przypadku zamiany: 0,667255
Jest to bardzo zbliżone do odpowiedzi, które dał nam schemat blokowy.
W rzeczywistości im częściej przeprowadzamy tę symulację, tym bardziej odpowiedź zbliża się do prawdziwej wartości, a tym samym potwierdza prawo wielkich liczb:
To samo widać z tej tabeli:
| Symulacje działają | Prawdopodobieństwo wygranej w przypadku zmiany | Prawdopodobieństwo wygranej, jeśli się nie zmienisz |
| 10 | 0,6 | 0,2 |
| 10^2 | 0,63 | 0,33 |
| 10^3 | 0,661 | 0,333 |
| 10^4 | 0,6683 | 0,3236 |
| 10^5 | 0,66762 | 0,33171 |
| 10^6 | 0,667255 | 0,334134 |
| 10^7 | 0,6668756 | 0,3332821 |
Bayesowski sposób myślenia
„Frequentystka, znana jako bardziej klasyczna wersja statystyki, zakłada, że prawdopodobieństwo to długoterminowa częstotliwość zdarzeń (stąd nadany tytuł)”.
„Statystyka bayesowska to teoria w dziedzinie statystyki oparta na bayesowskiej interpretacji prawdopodobieństwa, w której prawdopodobieństwo wyraża stopień wiary w zdarzenie. Stopień przekonania może opierać się na wcześniejszej wiedzy o wydarzeniu, takiej jak wyniki poprzednich eksperymentów, lub na osobistych przekonaniach na temat wydarzenia”. - z programowania probabilistycznego i metod bayesowskich dla hakerów
Co to znaczy?
W częstym myśleniu patrzymy na prawdopodobieństwa na dłuższą metę. Kiedy bywalca mówi, że istnieje 0,001% szansy na wypadek samochodowy, oznacza to, że jeśli weźmiemy pod uwagę niekończące się podróże samochodem, 0,001% z nich zakończy się wypadkiem.
Bayesowski sposób myślenia jest inny, ponieważ zaczynamy od uprzedniego przekonania. Jeśli mówimy o przekonaniu 0, oznacza to, że uważasz, że wydarzenie nigdy się nie wydarzy; odwrotnie, przekonanie o wartości 1 oznacza, że jesteś pewien, że tak się stanie.
Następnie, gdy zaczniemy obserwować dane, aktualizujemy to przekonanie, aby uwzględnić dane. Jak to robimy? Korzystając z twierdzenia Bayesa.
Twierdzenie Bayesa
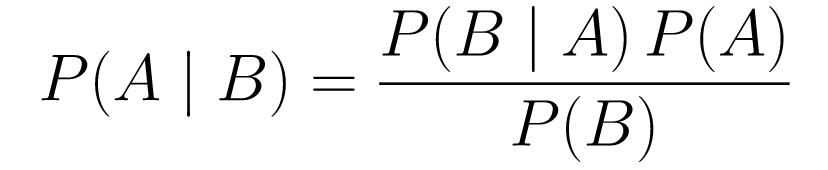 ....(1)
....(1)Rozbijmy to.
-
P(A | B)daje nam prawdopodobieństwo zdarzenia A danego zdarzenia B. To jest a posteriori, B to dane, które zaobserwowaliśmy, więc zasadniczo mówimy, jakie jest prawdopodobieństwo zajścia zdarzenia, biorąc pod uwagę dane, które zaobserwowaliśmy. -
P(A)to przeor, nasze przekonanie, że wydarzy się zdarzenie A. -
P(B | A)to prawdopodobieństwo, jakie jest prawdopodobieństwo, że będziemy obserwować dane, jeśli A jest prawdziwe.
Spójrzmy na przykład, test przesiewowy na raka.
Prawdopodobieństwo raka
Powiedzmy, że pacjentka idzie na mammografię i wynik mammografii jest pozytywny. Jakie jest prawdopodobieństwo, że pacjent rzeczywiście ma raka?
Zdefiniujmy prawdopodobieństwa:
- 1% kobiet ma raka piersi.
- Mammogramy wykrywają raka w 80% przypadków, w których jest on rzeczywiście obecny.
- 9,6% mammogramów fałszywie informuje, że masz raka, podczas gdy w rzeczywistości go nie masz.
Tak więc, jeśli miałbyś powiedzieć, że jeśli mammografia ma pozytywne znaczenie, istnieje 80% szans, że masz raka, to byłoby źle. Nie wziąłbyś pod uwagę, że zachorowanie na raka jest rzadkim zdarzeniem, tj. tylko 1% kobiet ma raka piersi. Musimy przyjąć to tak, jak wcześniej, i tutaj w grę wchodzi twierdzenie Bayesa:
P(C+ | T+) =(P(T+|C+)*P(C+))/P(T+)
-
P(C+ | T+): To jest prawdopodobieństwo obecności raka, biorąc pod uwagę, że test był pozytywny, to nas interesuje. -
P(T+ | C+): Jest to prawdopodobieństwo, że test jest pozytywny, biorąc pod uwagę, że jest rak, to, jak omówiono powyżej, wynosi 80% = 0,8. -
P(C+): Jest to prawdopodobieństwo a priori, prawdopodobieństwo zachorowania na raka, które wynosi 1% = 0,01. -
P(T+): Jest to prawdopodobieństwo, że test jest pozytywny, bez względu na wszystko, więc składa się z dwóch składników: P(T+) = P(T+|C-) P(C-)+P(T+|C+) P (C+) -
P(T+ | C-): Jest to prawdopodobieństwo, że wynik testu jest pozytywny, ale nie ma raka, jest to 0,096. -
P(C-): Jest to prawdopodobieństwo braku raka, ponieważ prawdopodobieństwo zachorowania na raka wynosi 1%, to jest równe 99% = 0,99. -
P(T+ | C+): Jest to prawdopodobieństwo, że wynik testu jest pozytywny, biorąc pod uwagę, że masz raka, wynosi ono 80% = 0,8. -
P(C+): Jest to prawdopodobieństwo zachorowania na raka, które wynosi 1% = 0,01.
Podłączając to wszystko do oryginalnej formuły:
Tak więc, biorąc pod uwagę, że wynik mammografii był pozytywny, istnieje 7,76% szans na raka u pacjentki. Na początku może wydawać się to dziwne, ale ma sens. Test daje fałszywie pozytywny wynik w 9,6% przypadków (dość wysoki), więc w danej populacji będzie wiele fałszywie pozytywnych wyników. W przypadku rzadkiej choroby większość pozytywnych wyników testów będzie błędna.
Wróćmy teraz do problemu Monty'ego Halla i rozwiążmy go za pomocą twierdzenia Bayesa.
Problem Monty'ego Halla
Priory można zdefiniować jako:

- Załóżmy, że na początku wybrałeś drzwi A.
- P(H) = , ⅓. ⅓ dla wszystkich trzech drzwi, co oznacza, że zanim drzwi się otworzyły i pojawiła się koza, istniała taka sama szansa, że za którymś z nich znajdzie się samochód.
Prawdopodobieństwo można zdefiniować jako:
-
P(D|H), gdzie zdarzenie D polega na tym, że Monty wybiera drzwi B i nie ma za nimi samochodu. -
P(D|H)= 1/2 jeśli samochód jest za drzwiami A - ponieważ jest 50% szansy, że wybierze drzwi B i 50% szansy, że wybierze drzwi C. -
P(D|H)= 0, jeśli samochód znajduje się za drzwiami B, ponieważ istnieje 0% szansy, że wybierze drzwi B, jeśli samochód jest za nimi. -
P(D|H)= 1 jeśli samochód jest za C, a Ty wybierzesz A, jest 100% prawdopodobieństwa, że wybierze drzwi B.
Interesuje nas P(H|D) , czyli prawdopodobieństwo, że samochód jest za drzwiami, biorąc pod uwagę, że pokazuje nam kozę za jednymi z pozostałych drzwi.
Z tyłu, P(H|D) widać, że przejście do drzwi C z A zwiększy prawdopodobieństwo wygranej.
Metropolis-Hastings
Teraz połączmy wszystko, co omówiliśmy do tej pory i spróbujmy zrozumieć, jak działa Metropolis-Hastings.
Metropolis-Hastings wykorzystuje twierdzenie Bayesa, aby uzyskać rozkład a posteriori złożonego rozkładu, z którego bezpośrednie próbkowanie jest trudne.
W jaki sposób? Zasadniczo wybiera losowo różne próbki z przestrzeni i sprawdza, czy nowa próbka jest bardziej prawdopodobna z tyłu niż ostatnia, ponieważ patrzymy na stosunek prawdopodobieństw, P(B) w równaniu (1), otrzymuje anulowane:
P(akceptacja) = ( P(nowaPróbka) * Prawdopodobieństwo nowej próbki) / (P(staraPróbka) * Prawdopodobieństwo starej próbki)
O „prawdopodobieństwie” każdej nowej próbki decyduje funkcja f . Dlatego f musi być proporcjonalne do a posteriori, z którego chcemy próbkować.
Aby zdecydować, czy θ′ ma być zaakceptowane, czy odrzucone, dla każdego nowego proponowanego θ należy obliczyć następujący stosunek:
Gdzie θ jest starą próbką, P(D| θ) jest prawdopodobieństwem próby θ.
Posłużmy się przykładem, aby lepiej to zrozumieć. Załóżmy, że masz dane, ale chcesz znaleźć rozkład normalny, który do nich pasuje, więc:
X ~ N (średnia, standardowa)
Teraz musimy zdefiniować a priori dla średniej i std. Dla uproszczenia przyjmiemy, że oba mają rozkład normalny ze średnią 1 i std 2:
Średnia ~ N(1, 2)
std ~ N(1, 2)
Teraz wygenerujmy trochę danych i załóżmy, że rzeczywista średnia i std wynoszą odpowiednio 0,5 i 1,2.
import numpy as np import matplotlib.pyplot as plt import scipy.stats as st meanX = 1.5 stdX = 1.2 X = np.random.normal(meanX, stdX, size = 1000) _ = plt.hist(X, bins = 50)PyMC3
Najpierw użyjmy biblioteki o nazwie PyMC3 do modelowania danych i znalezienia rozkładu a posteriori dla średniej i std.
import pymc3 as pm with pm.Model() as model: mean = pm.Normal("mean", mu = 1, sigma = 2) std = pm.Normal("std", mu = 1, sigma = 2) x = pm.Normal("X", mu = mean, sigma = std, observed = X) step = pm.Metropolis() trace = pm.sample(5000, step = step)Przejdźmy przez kod.
Najpierw definiujemy a priori dla średniej i std, tj. normalną ze średnią 1 i std 2.
x = pm.Normal(„X”, mu = średnia, sigma = std, obserwowane = X)
W tym wierszu definiujemy interesującą nas zmienną; bierze średnią i std, które zdefiniowaliśmy wcześniej, bierze również obserwowane wartości, które obliczyliśmy wcześniej.
Spójrzmy na wyniki:
_ = plt.hist(trace['std'], bins = 50, label = "std") _ = plt.hist(trace['mean'], bins = 50, label = "mean") _ = plt.legend()Standard jest wyśrodkowany wokół 1,2, a średnia wynosi 1,55 - całkiem blisko!
Zróbmy to teraz od zera, aby zrozumieć Metropolis-Hastings.
Od zera
Generowanie propozycji
Najpierw zrozummy, czym zajmuje się Metropolis-Hastings. Wcześniej w tym artykule powiedzieliśmy: „Metropolis-Hastings losowo wybiera różne próbki z kosmosu”, ale skąd wie, którą próbkę wybrać?
Robi to za pomocą dystrybucji propozycji. Jest to rozkład normalny skoncentrowany na aktualnie akceptowanej próbce i ma STD równy 0,5. Gdzie 0.5 jest hiperparametrem, możemy poprawić; im więcej STD propozycji, tym dalej będzie przeszukiwać aktualnie zaakceptowaną próbkę. Zakodujmy to.
Ponieważ musimy znaleźć średnią i std rozkładu, ta funkcja pobierze aktualnie akceptowaną średnią i aktualnie akceptowaną std i zwróci propozycje dla obu.
def get_proposal(mean_current, std_current, proposal_width = 0.5): return np.random.normal(mean_current, proposal_width), \ np.random.normal(std_current, proposal_width)Przyjęcie/odrzucenie propozycji
Teraz zakodujmy logikę, która akceptuje lub odrzuca propozycję. Składa się z dwóch części: a priori i prawdopodobieństwa .
Najpierw obliczmy prawdopodobieństwo, że propozycja pochodzi od poprzedniego:
def prior(mean, std, prior_mean, prior_std): return st.norm(prior_mean[0], prior_mean[1]).pdf(mean)* \ st.norm(prior_std[0], prior_std[1]).pdf(std)Po prostu bierze średnią i std i oblicza prawdopodobieństwo, że ta średnia i std pochodzą z poprzedniego rozkładu , który zdefiniowaliśmy.
Obliczając prawdopodobieństwo, obliczamy prawdopodobieństwo, że dane, które widzieliśmy, pochodzą z proponowanego rozkładu.
def likelihood(mean, std, data): return np.prod(st.norm(mean, std).pdf(X))Tak więc dla każdego punktu danych mnożymy prawdopodobieństwo, że ten punkt danych pochodzi z proponowanego rozkładu.
Teraz musimy wywołać te funkcje dla aktualnego mean i std oraz dla proponowanego mean i std .
prior_current = prior(mean_current, std_current, prior_mean, prior_std) likelihood_current = likelihood(mean_current, std_current, data) prior_proposal = prior(mean_proposal, std_proposal, prior_mean, prior_std) likelihood_proposal = likelihood(mean_proposal, std_proposal, data)Cały kod:
def accept_proposal(mean_proposal, std_proposal, mean_current, \ std_current, prior_mean, prior_std, data): def prior(mean, std, prior_mean, prior_std): return st.norm(prior_mean[0], prior_mean[1]).pdf(mean)* \ st.norm(prior_std[0], prior_std[1]).pdf(std) def likelihood(mean, std, data): return np.prod(st.norm(mean, std).pdf(X)) prior_current = prior(mean_current, std_current, prior_mean, prior_std) likelihood_current = likelihood(mean_current, std_current, data) prior_proposal = prior(mean_proposal, std_proposal, prior_mean, prior_std) likelihood_proposal = likelihood(mean_proposal, std_proposal, data) return (prior_proposal * likelihood_proposal) / (prior_current * likelihood_current)Teraz stwórzmy ostateczną funkcję, która połączy wszystko razem i wygeneruje potrzebne nam próbki.
Generowanie tylnego
Teraz wywołujemy funkcje, które napisaliśmy powyżej i generujemy a posteriori!
def get_trace(data, samples = 5000): mean_prior = 1 std_prior = 2 mean_current = mean_prior std_current = std_prior trace = { "mean": [mean_current], "std": [std_current] } for i in tqdm(range(samples)): mean_proposal, std_proposal = get_proposal(mean_current, std_current) acceptance_prob = accept_proposal(mean_proposal, std_proposal, mean_current, \ std_current, [mean_prior, std_prior], \ [mean_prior, std_prior], data) if np.random.rand() < acceptance_prob: mean_current = mean_proposal std_current = std_proposal trace['mean'].append(mean_current) trace['std'].append(std_current) return traceMiejsce na udoskonalenie
Log jest twoim przyjacielem!
Przypomnijmy a * b = antilog(log(a) + log(b)) i a / b = antilog(log(a) - log(b)).
Jest to dla nas korzystne, ponieważ będziemy mieli do czynienia z bardzo małymi prawdopodobieństwami, pomnożenie co da zero, więc raczej dodamy log prob, problem rozwiązany!
Tak więc nasz poprzedni kod staje się:
def accept_proposal(mean_proposal, std_proposal, mean_current, \ std_current, prior_mean, prior_std, data): def prior(mean, std, prior_mean, prior_std): return st.norm(prior_mean[0], prior_mean[1]).logpdf(mean)+ \ st.norm(prior_std[0], prior_std[1]).logpdf(std) def likelihood(mean, std, data): return np.sum(st.norm(mean, std).logpdf(X)) prior_current = prior(mean_current, std_current, prior_mean, prior_std) likelihood_current = likelihood(mean_current, std_current, data) prior_proposal = prior(mean_proposal, std_proposal, prior_mean, prior_std) likelihood_proposal = likelihood(mean_proposal, std_proposal, data) return (prior_proposal + likelihood_proposal) - (prior_current + likelihood_current)Ponieważ zwracamy log prawdopodobieństwa akceptacji:
if np.random.rand() < acceptance_prob:
Staje się:
if math.log(np.random.rand()) < acceptance_prob:
Uruchommy nowy kod i wykreślmy wyniki.
_ = plt.hist(trace['std'], bins = 50, label = "std") _ = plt.hist(trace['mean'], bins = 50, label = "mean") _ = plt.legend()Jak widać, std jest wyśrodkowany na 1,2, a średnia na 1,5. Zrobiliśmy to!
Posuwając się do przodu
Do tej pory mam nadzieję, że rozumiesz, jak działa Metropolis-Hastings i możesz się zastanawiać, gdzie możesz go użyć.
Cóż, Bayesian Methods for Hackers to doskonała książka, która wyjaśnia programowanie probabilistyczne, a jeśli chcesz dowiedzieć się więcej o twierdzeniu Bayesa i jego zastosowaniach, Think Bayes to świetna książka autorstwa Allena B. Downeya.
Dziękuję za przeczytanie i mam nadzieję, że ten artykuł zachęci Cię do odkrycia niesamowitego świata statystyk Bayesa.
