Métodos MCMC: Metropolis-Hastings e Inferência Bayesiana
Publicados: 2022-03-11Vamos tirar a definição básica do caminho: os métodos Markov Chain Monte Carlo (MCMC) nos permitem calcular amostras de uma distribuição mesmo que não possamos computá-la.
O que isto significa? Vamos voltar e falar sobre Monte Carlo Sampling.
Amostragem de Monte Carlo
O que são métodos de Monte Carlo?
“Os métodos de Monte Carlo, ou experimentos de Monte Carlo, são uma ampla classe de algoritmos computacionais que dependem de amostragem aleatória repetida para obter resultados numéricos”. (Wikipédia)
Vamos quebrar isso.
Exemplo 1: Estimativa de Área
Imagine que você tenha uma forma irregular, como a forma apresentada abaixo:
E você tem a tarefa de determinar a área delimitada por essa forma. Um dos métodos que você pode usar é fazer pequenos quadrados na forma, contar os quadrados, e isso lhe dará uma aproximação bastante precisa da área. No entanto, isso é difícil e demorado.
Amostragem de Monte Carlo para o resgate!
Primeiro, desenhamos um grande quadrado de uma área conhecida ao redor da forma, por exemplo de 50 cm2. Agora nós “penduramos” este quadrado e começamos a jogar dardos aleatoriamente na forma.
Em seguida, contamos o número total de dardos no retângulo e o número de dardos na forma que nos interessa. Vamos supor que o número total de “dardos” usados foi 100 e que 22 deles acabaram dentro da forma. Agora a área pode ser calculada pela fórmula simples:
área da forma = área do quadrado *(número de dardos na forma) / (número de dardos no quadrado)
Então, no nosso caso, isso se resume a:
área da forma = 50 * 22/100 = 11 cm2
Se multiplicarmos o número de “dardos” por um fator de 10, essa aproximação fica muito próxima da resposta real:
área da forma = 50 * 280/1000 = 14 cm2
É assim que dividimos tarefas complicadas, como a apresentada acima, usando a amostragem de Monte Carlo.
A Lei dos Grandes Números
A aproximação da área foi mais próxima quanto mais dardos atiramos, e isso é por causa da Lei dos Grandes Números:
“A lei dos grandes números é um teorema que descreve o resultado de realizar o mesmo experimento um grande número de vezes. De acordo com a lei, a média dos resultados obtidos em um grande número de tentativas deve estar próxima do valor esperado e tenderá a se aproximar à medida que mais tentativas forem realizadas.”
Isso nos leva ao nosso próximo exemplo, o famoso problema de Monty Hall.
Exemplo 2: O Problema de Monty Hall
O problema de Monty Hall é um quebra-cabeças muito famoso:
“Há três portas, uma tem um carro atrás, as outras têm uma cabra atrás delas. Você escolhe uma porta, o anfitrião abre uma porta diferente e mostra que há uma cabra atrás dela. Ele então pergunta se você quer mudar sua decisão. Você? Por quê? Por que não?"
A primeira coisa que vem à sua mente é que as chances de ganhar são iguais, quer você troque ou não, mas isso não é verdade. Vamos fazer um fluxograma simples para demonstrar o mesmo.
Supondo que o carro esteja atrás da porta 3:
Portanto, se você trocar, você ganha ⅔ vezes, e se não trocar, você ganha apenas ⅓ vezes.
Vamos resolver isso usando amostragem.
wins = [] for i in range(int(10e6)): car_door = assign_car_door() choice = random.randint(0, 2) opened_door = assign_door_to_open(car_door) did_he_win = win_or_lose(choice, car_door, opened_door, switch = False) wins.append(did_he_win) print(sum(wins)/len(wins)) A função assign_car_door() é apenas um gerador de números aleatórios que seleciona uma porta 0, 1 ou 2, atrás da qual há um carro. Usar assign_door_to_open seleciona uma porta que tem uma cabra atrás dela e não é a que você selecionou, e o host a abre. win_or_lose retorna true ou false , denotando se você ganhou o carro ou não, leva um bool “switch” que diz se você trocou a porta ou não.
Vamos executar esta simulação 10 milhões de vezes:
- Probabilidade de ganhar se você não trocar: 0,334134
- Probabilidade de ganhar se você trocar: 0,667255
Isso está muito próximo das respostas que o fluxograma nos deu.
Na verdade, quanto mais rodamos essa simulação, mais próxima a resposta fica do valor verdadeiro, validando assim a lei dos grandes números:
O mesmo pode ser visto nesta tabela:
| Simulações executadas | Probabilidade de ganhar se você trocar | Probabilidade de ganhar se você não trocar |
| 10 | 0,6 | 0,2 |
| 10^2 | 0,63 | 0,33 |
| 10^3 | 0,661 | 0,333 |
| 10^4 | 0,6683 | 0,3236 |
| 10^5 | 0,66762 | 0,33171 |
| 10^6 | 0,667255 | 0,334134 |
| 10^7 | 0,6668756 | 0,3332821 |
O Modo Bayesiano de Pensar
“Frequentista, conhecido como a versão mais clássica da estatística, assume que a probabilidade é a frequência de eventos de longo prazo (daí o título concedido).”
“A estatística bayesiana é uma teoria no campo da estatística baseada na interpretação bayesiana da probabilidade, onde a probabilidade expressa um grau de crença em um evento. O grau de crença pode ser baseado em conhecimento prévio sobre o evento, como os resultados de experimentos anteriores, ou em crenças pessoais sobre o evento”. - de Programação Probabilística e Métodos Bayesianos para Hackers
O que isto significa?
Na maneira freqüentista de pensar, olhamos para as probabilidades a longo prazo. Quando um frequentista diz que há 0,001% de chance de um acidente de carro acontecer, significa que, se considerarmos infinitas viagens de carro, 0,001% delas terminarão em acidente.
Uma mentalidade bayesiana é diferente, pois começamos com um a priori, uma crença. Se falamos de uma crença de 0, significa que sua crença é que o evento nunca acontecerá; inversamente, uma crença de 1 significa que você tem certeza de que isso acontecerá.
Então, uma vez que começamos a observar os dados, atualizamos essa crença para levar em consideração os dados. Como vamos fazer isso? Usando o teorema de Bayes.
Teorema de Bayes
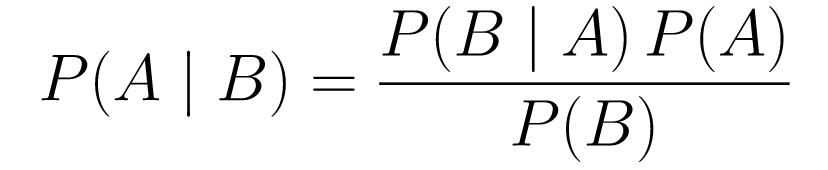 ....(1)
....(1)Vamos decompô-lo.
-
P(A | B)nos dá a probabilidade do evento A dado o evento B. Esta é a posterior, B são os dados que observamos, então estamos essencialmente dizendo qual é a probabilidade de um evento acontecer, considerando os dados que observamos. -
P(A)é o anterior, nossa crença de que o evento A acontecerá. -
P(B | A)é a probabilidade, qual é a probabilidade de observarmos os dados, dado que A é verdadeiro.
Vejamos um exemplo, o teste de rastreio do cancro.
Probabilidade de Câncer
Digamos que uma paciente vá fazer uma mamografia e a mamografia dê positivo. Qual é a probabilidade de que o paciente realmente tenha câncer?
Vamos definir as probabilidades:
- 1% das mulheres tem câncer de mama.
- As mamografias detectam o câncer em 80% das vezes quando ele está realmente presente.
- 9,6% das mamografias relatam falsamente que você tem câncer quando na verdade não o tem.
Então, se você disser que se uma mamografia deu positivo, significando que há 80% de chance de você ter câncer, isso estaria errado. Você não levaria em consideração que ter câncer é um evento raro, ou seja, que apenas 1% das mulheres tem câncer de mama. Precisamos tomar isso como anterior, e é aqui que o teorema de Bayes entra em jogo:
P(C+ | T+) =(P(T+|C+)*P(C+))/P(T+)
-
P(C+ | T+): Esta é a probabilidade de que o câncer esteja lá, dado que o teste foi positivo, é isso que nos interessa. -
P(T+ | C+): Esta é a probabilidade de que o teste seja positivo, dado que há câncer, isso, como discutido acima, é igual a 80% = 0,8. -
P(C+): Esta é a probabilidade anterior, a probabilidade de um indivíduo ter câncer, que é igual a 1% = 0,01. -
P(T+): Esta é a probabilidade de que o teste seja positivo, não importa o que aconteça, então tem dois componentes: P(T+) = P(T+|C-) P(C-)+P(T+|C+) P (C+) -
P(T+ | C-): Esta é a probabilidade de que o teste deu positivo, mas não há câncer, isso é dado por 0,096. -
P(C-): Esta é a probabilidade de não ter câncer, pois a probabilidade de ter câncer é de 1%, isto é igual a 99% = 0,99. -
P(T+ | C+): Esta é a probabilidade de que o teste tenha dado positivo, dado que você tem câncer, isso é igual a 80% = 0,8. -
P(C+): Esta é a probabilidade de ter câncer, que é igual a 1% = 0,01.
Colocando tudo isso na fórmula original:
Então, dado que a mamografia deu positivo, há 7,76% de chance de a paciente ter câncer. Pode parecer estranho no começo, mas faz sentido. O teste dá um falso positivo 9,6% das vezes (bastante alto), então haverá muitos falsos positivos em uma determinada população. Para uma doença rara, a maioria dos resultados positivos do teste estará errado.
Vamos agora revisitar o problema de Monty Hall e resolvê-lo usando o teorema de Bayes.
Problema de Monty Hall
Os antecedentes podem ser definidos como:

- Suponha que você escolheu a porta A como sua escolha no início.
- P(H) = ⅓, ⅓. ⅓ para todas as três portas, o que significa que antes que a porta fosse aberta e a cabra revelada, havia uma chance igual de o carro estar atrás de qualquer uma delas.
A probabilidade pode ser definida como:
-
P(D|H), onde o evento D é que Monty escolhe a porta B e não há nenhum carro atrás dela. -
P(D|H)= 1/2 se o carro estiver atrás da porta A - pois há 50% de chance de ele escolher a porta B e 50% de chance de ele escolher a porta C. -
P(D|H)= 0 se o carro estiver atrás da porta B, pois há 0% de chance de ele escolher a porta B se o carro estiver atrás dela. -
P(D|H)= 1 se o carro estiver atrás de C e você escolher A, há 100% de probabilidade de que ele escolha a porta B.
Estamos interessados em P(H|D) , que é a probabilidade de que o carro esteja atrás de uma porta, dado que ela nos mostra uma cabra atrás de uma das outras portas.
Pode-se ver a posteriori, P(H|D) , que mudar para a porta C de A aumentará a probabilidade de ganhar.
Metrópole-Hastings
Agora, vamos combinar tudo o que cobrimos até agora e tentar entender como Metropolis-Hastings funciona.
Metropolis-Hastings usa o teorema de Bayes para obter a distribuição posterior de uma distribuição complexa, da qual a amostragem direta é difícil.
Quão? Essencialmente, ele seleciona aleatoriamente diferentes amostras de um espaço e verifica se a nova amostra é mais provável de ser a posterior do que a última amostra, já que estamos olhando para a razão de probabilidades, P(B) na equação (1), obtém cancelado:
P(aceitação) = ( P(nova amostra) * Probabilidade de nova amostra) / (P(antiga amostra) * Probabilidade de amostra antiga)
A “probabilidade” de cada nova amostra é decidida pela função f . É por isso que f deve ser proporcional à posterior da qual queremos amostrar.
Para decidir se θ′ deve ser aceito ou rejeitado, a seguinte razão deve ser calculada para cada novo θ' proposto:
Onde θ é a amostra antiga, P(D| θ) é a probabilidade da amostra θ.
Vamos usar um exemplo para entender isso melhor. Digamos que você tenha dados, mas queira descobrir a distribuição normal que se ajusta a eles, então:
X ~ N (média, padrão)
Agora precisamos definir os priors para a média e std ambos. Para simplificar, vamos supor que ambos seguem uma distribuição normal com média 1 e std 2:
Média ~ N(1, 2)
padrão ~ N(1, 2)
Agora, vamos gerar alguns dados e assumir que a verdadeira média e std são 0,5 e 1,2, respectivamente.
import numpy as np import matplotlib.pyplot as plt import scipy.stats as st meanX = 1.5 stdX = 1.2 X = np.random.normal(meanX, stdX, size = 1000) _ = plt.hist(X, bins = 50)PyMC3
Vamos primeiro usar uma biblioteca chamada PyMC3 para modelar os dados e encontrar a distribuição posterior para a média e std.
import pymc3 as pm with pm.Model() as model: mean = pm.Normal("mean", mu = 1, sigma = 2) std = pm.Normal("std", mu = 1, sigma = 2) x = pm.Normal("X", mu = mean, sigma = std, observed = X) step = pm.Metropolis() trace = pm.sample(5000, step = step)Vamos repassar o código.
Primeiro, definimos a priori para média e std, ou seja, uma normal com média 1 e std 2.
x = pm.Normal(“X”, mu = média, sigma = std, observado = X)
Nesta linha, definimos a variável que nos interessa; leva a média e std que definimos anteriormente, também leva valores observados que calculamos anteriormente.
Vejamos os resultados:
_ = plt.hist(trace['std'], bins = 50, label = "std") _ = plt.hist(trace['mean'], bins = 50, label = "mean") _ = plt.legend()O std está centrado em torno de 1,2, e a média é de 1,55 - bem próximo!
Vamos agora fazer do zero para entender Metropolis-Hastings.
Do princípio
Gerando uma proposta
Primeiro, vamos entender o que Metropolis-Hastings faz. Anteriormente neste artigo, dissemos: “Metropolis-Hastings seleciona aleatoriamente diferentes amostras de um espaço”, mas como ele sabe qual amostra selecionar?
Ele faz isso usando a distribuição da proposta. É uma distribuição normal centrada na amostra atualmente aceita e tem um STD de 0,5. Onde 0,5 é um hiperparâmetro, podemos ajustar; quanto maior for o STD da proposta, mais longe será a busca da amostra atualmente aceita. Vamos codificar isso.
Como temos que encontrar a média e o std da distribuição, essa função pegará a média atualmente aceita e o std atualmente aceito e retornará propostas para ambos.
def get_proposal(mean_current, std_current, proposal_width = 0.5): return np.random.normal(mean_current, proposal_width), \ np.random.normal(std_current, proposal_width)Aceitando/Rejeitando uma Proposta
Agora, vamos codificar a lógica que aceita ou rejeita a proposta. Tem duas partes: a anterior e a probabilidade .
Primeiro, vamos calcular a probabilidade da proposta vir do anterior:
def prior(mean, std, prior_mean, prior_std): return st.norm(prior_mean[0], prior_mean[1]).pdf(mean)* \ st.norm(prior_std[0], prior_std[1]).pdf(std)Ele apenas pega a média e std e calcula a probabilidade de que essa média e std venham da distribuição anterior que definimos.
Ao calcular a probabilidade, calculamos a probabilidade de os dados que vimos terem vindo da distribuição proposta.
def likelihood(mean, std, data): return np.prod(st.norm(mean, std).pdf(X))Então, para cada ponto de dados, multiplicamos a probabilidade desse ponto de dados vir da distribuição proposta.
Agora, precisamos chamar essas funções para a média atual e std e para a média e std propostas.
prior_current = prior(mean_current, std_current, prior_mean, prior_std) likelihood_current = likelihood(mean_current, std_current, data) prior_proposal = prior(mean_proposal, std_proposal, prior_mean, prior_std) likelihood_proposal = likelihood(mean_proposal, std_proposal, data)Todo o código:
def accept_proposal(mean_proposal, std_proposal, mean_current, \ std_current, prior_mean, prior_std, data): def prior(mean, std, prior_mean, prior_std): return st.norm(prior_mean[0], prior_mean[1]).pdf(mean)* \ st.norm(prior_std[0], prior_std[1]).pdf(std) def likelihood(mean, std, data): return np.prod(st.norm(mean, std).pdf(X)) prior_current = prior(mean_current, std_current, prior_mean, prior_std) likelihood_current = likelihood(mean_current, std_current, data) prior_proposal = prior(mean_proposal, std_proposal, prior_mean, prior_std) likelihood_proposal = likelihood(mean_proposal, std_proposal, data) return (prior_proposal * likelihood_proposal) / (prior_current * likelihood_current)Agora, vamos criar a função final que unirá tudo e gerará as amostras posteriores que precisamos.
Gerando o Posterior
Agora, chamamos as funções que escrevemos acima e geramos o posterior!
def get_trace(data, samples = 5000): mean_prior = 1 std_prior = 2 mean_current = mean_prior std_current = std_prior trace = { "mean": [mean_current], "std": [std_current] } for i in tqdm(range(samples)): mean_proposal, std_proposal = get_proposal(mean_current, std_current) acceptance_prob = accept_proposal(mean_proposal, std_proposal, mean_current, \ std_current, [mean_prior, std_prior], \ [mean_prior, std_prior], data) if np.random.rand() < acceptance_prob: mean_current = mean_proposal std_current = std_proposal trace['mean'].append(mean_current) trace['std'].append(std_current) return traceEspaço para melhorias
Log é seu amigo!
Lembre-se a * b = antilog(log(a) + log(b)) e a / b = antilog(log(a) - log(b)).
Isso é benéfico para nós porque estaremos lidando com probabilidades muito pequenas, multiplicando o que resultará em zero, então vamos adicionar o log prob, problema resolvido!
Então, nosso código anterior se torna:
def accept_proposal(mean_proposal, std_proposal, mean_current, \ std_current, prior_mean, prior_std, data): def prior(mean, std, prior_mean, prior_std): return st.norm(prior_mean[0], prior_mean[1]).logpdf(mean)+ \ st.norm(prior_std[0], prior_std[1]).logpdf(std) def likelihood(mean, std, data): return np.sum(st.norm(mean, std).logpdf(X)) prior_current = prior(mean_current, std_current, prior_mean, prior_std) likelihood_current = likelihood(mean_current, std_current, data) prior_proposal = prior(mean_proposal, std_proposal, prior_mean, prior_std) likelihood_proposal = likelihood(mean_proposal, std_proposal, data) return (prior_proposal + likelihood_proposal) - (prior_current + likelihood_current)Como estamos retornando o log de probabilidade de aceitação:
if np.random.rand() < acceptance_prob:
Torna-se:
if math.log(np.random.rand()) < acceptance_prob:
Vamos executar o novo código e plotar os resultados.
_ = plt.hist(trace['std'], bins = 50, label = "std") _ = plt.hist(trace['mean'], bins = 50, label = "mean") _ = plt.legend()Como você pode ver, o std está centrado em 1,2 e a média em 1,5. Conseguimos!
Seguindo em frente
Até agora, você espera que entenda como Metropolis-Hastings funciona e pode estar se perguntando onde pode usá-lo.
Bem, Bayesian Methods for Hackers é um excelente livro que explica programação probabilística, e se você quiser aprender mais sobre o teorema de Bayes e suas aplicações, Think Bayes é um ótimo livro de Allen B. Downey.
Obrigado por ler, e espero que este artigo o encoraje a descobrir o incrível mundo das estatísticas Bayesianas.
