Metode MCMC: Metropolis-Hastings dan Inferensi Bayesian
Diterbitkan: 2022-03-11Mari kita singkirkan definisi dasarnya: Metode Markov Chain Monte Carlo (MCMC) memungkinkan kita menghitung sampel dari suatu distribusi meskipun kita tidak dapat menghitungnya.
Apa artinya ini? Mari kita kembali dan berbicara tentang Pengambilan Sampel Monte Carlo.
Pengambilan Sampel Monte Carlo
Apa itu metode Monte Carlo?
“Metode Monte Carlo, atau eksperimen Monte Carlo, adalah kelas luas dari algoritma komputasi yang mengandalkan pengambilan sampel acak berulang untuk mendapatkan hasil numerik.” (Wikipedia)
Mari kita hancurkan itu.
Contoh 1: Estimasi Area
Bayangkan Anda memiliki bentuk yang tidak beraturan, seperti bentuk yang disajikan di bawah ini:
Dan Anda ditugaskan untuk menentukan area yang dibatasi oleh bentuk ini. Salah satu metode yang dapat Anda gunakan adalah membuat kotak kecil dalam bentuk, menghitung kotak, dan itu akan memberi Anda perkiraan luas yang cukup akurat. Namun, itu sulit dan memakan waktu.
Pengambilan sampel Monte Carlo untuk menyelamatkan!
Pertama, kita menggambar persegi besar dari area yang diketahui di sekitar bentuk, misalnya 50 cm2. Sekarang kita "menggantung" kotak ini dan mulai melempar anak panah secara acak ke bentuknya.
Selanjutnya, kita menghitung jumlah total anak panah dalam persegi panjang dan jumlah anak panah dalam bentuk yang kita minati. Mari kita asumsikan bahwa jumlah total "anak panah" yang digunakan adalah 100 dan 22 di antaranya berakhir di dalam bentuk. Sekarang luasnya dapat dihitung dengan rumus sederhana:
luas bentuk = luas persegi *(jumlah anak panah dalam bentuk) / (jumlah anak panah dalam persegi)
Jadi, dalam kasus kami, ini bermuara pada:
luas bangun = 50 * 22/100 = 11 cm2
Jika kita mengalikan jumlah "anak panah" dengan faktor 10, perkiraan ini menjadi sangat dekat dengan jawaban sebenarnya:
luas bangun = 50 * 280/1000 = 14 cm2
Inilah cara kami memecah tugas-tugas rumit, seperti yang diberikan di atas, dengan menggunakan pengambilan sampel Monte Carlo.
Hukum Bilangan Besar
Pendekatan area semakin dekat semakin banyak anak panah yang kita lempar, dan ini karena Hukum Bilangan Besar:
“Hukum bilangan besar adalah teorema yang menjelaskan hasil dari melakukan eksperimen yang sama berkali-kali. Menurut hukum, rata-rata hasil yang diperoleh dari sejumlah besar percobaan harus mendekati nilai yang diharapkan, dan akan cenderung menjadi lebih dekat karena lebih banyak percobaan dilakukan.”
Ini membawa kita ke contoh berikutnya, masalah Monty Hall yang terkenal.
Contoh 2: Masalah Monty Hall
Masalah Monty Hall adalah permainan asah otak yang sangat terkenal:
“Ada tiga pintu, yang satu ada mobil di belakangnya, yang lain ada kambing di belakangnya. Anda memilih sebuah pintu, tuan rumah membuka pintu yang berbeda, dan menunjukkan ada seekor kambing di belakangnya. Dia kemudian bertanya apakah Anda ingin mengubah keputusan Anda. Apakah kamu? Mengapa? Kenapa tidak?"
Hal pertama yang terlintas dalam pikiran Anda adalah bahwa peluang untuk menang adalah sama apakah Anda beralih atau tidak, tetapi itu tidak benar. Mari kita buat diagram alur sederhana untuk menunjukkan hal yang sama.
Dengan asumsi bahwa mobil berada di belakang pintu 3:
Oleh karena itu, jika Anda beralih, Anda menang kali, dan jika Anda tidak beralih, Anda hanya menang kali.
Mari kita selesaikan ini dengan menggunakan sampling.
wins = [] for i in range(int(10e6)): car_door = assign_car_door() choice = random.randint(0, 2) opened_door = assign_door_to_open(car_door) did_he_win = win_or_lose(choice, car_door, opened_door, switch = False) wins.append(did_he_win) print(sum(wins)/len(wins)) Fungsi assign_car_door() hanyalah generator angka acak yang memilih pintu 0, 1, atau 2, di belakangnya ada mobil. Menggunakan assign_door_to_open memilih pintu yang memiliki kambing di belakangnya dan bukan yang Anda pilih, dan tuan rumah membukanya. win_or_lose mengembalikan true atau false , yang menunjukkan apakah Anda memenangkan mobil atau tidak, dibutuhkan "saklar" bool yang mengatakan apakah Anda mengganti pintu atau tidak.
Mari kita jalankan simulasi ini 10 juta kali:
- Probabilitas menang jika Anda tidak beralih: 0,334134
- Probabilitas menang jika Anda beralih: 0.667255
Ini sangat dekat dengan jawaban yang diberikan diagram alur kepada kami.
Faktanya, semakin banyak kita menjalankan simulasi ini, semakin dekat jawaban dengan nilai sebenarnya, sehingga memvalidasi hukum bilangan besar:
Hal yang sama dapat dilihat dari tabel ini:
| Simulasi berjalan | Probabilitas menang jika Anda beralih | Probabilitas menang jika Anda tidak beralih |
| 10 | 0.6 | 0.2 |
| 10^2 | 0.63 | 0.33 |
| 10^3 | 0.661 | 0,333 |
| 10^4 | 0,6683 | 0.3236 |
| 10^5 | 0.66762 | 0.33171 |
| 10^6 | 0.667255 | 0.334134 |
| 10^7 | 0.6668756 | 0.3332821 |
Cara Berpikir Bayesian
“Frequentist, yang dikenal sebagai versi statistik yang lebih klasik, berasumsi bahwa probabilitas adalah frekuensi kejadian jangka panjang (oleh karena itu gelar yang diberikan).”
“Statistik Bayesian adalah teori dalam bidang statistika yang didasarkan pada interpretasi Bayesian tentang probabilitas di mana probabilitas menyatakan suatu derajat kepercayaan terhadap suatu peristiwa. Tingkat kepercayaan mungkin didasarkan pada pengetahuan sebelumnya tentang peristiwa tersebut, seperti hasil eksperimen sebelumnya, atau pada keyakinan pribadi tentang peristiwa tersebut. - dari Pemrograman Probabilistik dan Metode Bayesian untuk Peretas
Apa artinya ini?
Dalam cara berpikir yang sering, kita melihat probabilitas dalam jangka panjang. Ketika seorang frequentist mengatakan bahwa ada kemungkinan 0,001% kecelakaan mobil terjadi, itu berarti, jika kita mempertimbangkan perjalanan mobil yang tak terbatas, 0,001% di antaranya akan berakhir dengan kecelakaan.
Pola pikir Bayesian berbeda, seperti yang kita mulai dengan sebelumnya, sebuah keyakinan. Jika kita berbicara tentang keyakinan 0, itu berarti keyakinan Anda adalah bahwa peristiwa itu tidak akan pernah terjadi; sebaliknya, keyakinan 1 berarti Anda yakin itu akan terjadi.
Kemudian, begitu kami mulai mengamati data, kami memperbarui keyakinan ini untuk mempertimbangkan data. Bagaimana kita melakukan ini? Dengan menggunakan teorema Bayes.
Teorema Bayes
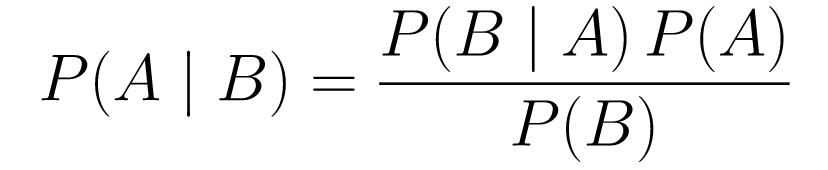 ....(1)
....(1)Mari kita hancurkan.
-
P(A | B)memberi kita peluang kejadian A diberikan kejadian B. Ini adalah posterior, B adalah data yang kita amati, jadi kita pada dasarnya mengatakan apa probabilitas suatu kejadian terjadi, dengan mempertimbangkan data yang kita amati. -
P(A)adalah prior, keyakinan kami bahwa peristiwa A akan terjadi. -
P(B | A)adalah peluang, berapa peluang bahwa kita akan mengamati data yang diberikan bahwa A benar.
Mari kita lihat sebuah contoh, tes skrining kanker.
Kemungkinan Kanker
Katakanlah seorang pasien pergi untuk melakukan mammogram, dan hasil mammogramnya kembali positif. Berapa probabilitas bahwa pasien benar-benar menderita kanker?
Mari kita tentukan probabilitasnya:
- 1% wanita menderita kanker payudara.
- Mammogram mendeteksi kanker 80% dari waktu ketika itu benar-benar ada.
- 9,6% mammogram secara keliru melaporkan bahwa Anda menderita kanker padahal sebenarnya Anda tidak mengidapnya.
Jadi, jika Anda mengatakan bahwa jika hasil mammogram menunjukkan hasil positif yang berarti ada kemungkinan 80% Anda terkena kanker, itu salah. Anda tidak akan mempertimbangkan bahwa menderita kanker adalah peristiwa yang langka, yaitu, hanya 1% wanita yang menderita kanker payudara. Kita perlu menganggap ini sebagai sebelumnya, dan di sinilah teorema Bayes berperan:
P(C+ | T+) =(P(T+|C+)*P(C+))/P(T+)
-
P(C+ | T+): Ini adalah kemungkinan adanya kanker, mengingat tesnya positif, inilah yang kami minati. -
P(T+ | C+): Ini adalah probabilitas bahwa tesnya positif, mengingat ada kanker, ini, seperti yang dibahas di atas adalah sama dengan 80% = 0,8. -
P(C+): Ini adalah peluang sebelumnya, peluang seseorang terkena kanker, yaitu sama dengan 1% = 0,01. -
P(T+): Ini adalah probabilitas bahwa tes positif, apa pun yang terjadi, sehingga memiliki dua komponen: P(T+) = P(T+|C-) P(C-)+P(T+|C+) P (C+) -
P(T+ | C-): Ini adalah probabilitas bahwa tes kembali positif tetapi tidak ada kanker, ini diberikan oleh 0,096. -
P(C-): Ini adalah peluang tidak terkena kanker karena peluang terkena kanker adalah 1%, ini sama dengan 99% = 0,99. -
P(T+ | C+): Ini adalah probabilitas bahwa tes kembali positif, mengingat Anda menderita kanker, ini sama dengan 80% = 0,8. -
P(C+): Ini adalah probabilitas menderita kanker, yang sama dengan 1% = 0,01.
Memasukkan semua ini ke dalam rumus asli:
Jadi, mengingat hasil mammogramnya positif, maka ada kemungkinan 7,76% pasien tersebut terkena kanker. Ini mungkin tampak aneh pada awalnya, tetapi itu masuk akal. Tes memberikan positif palsu 9,6% dari waktu (cukup tinggi), sehingga akan ada banyak positif palsu dalam populasi tertentu. Untuk penyakit langka, sebagian besar hasil tes positif akan salah.
Mari kita sekarang meninjau kembali masalah Monty Hall dan menyelesaikannya menggunakan teorema Bayes.

Masalah Monty Hall
Prior dapat didefinisikan sebagai:
- Asumsikan Anda memilih pintu A sebagai pilihan Anda di awal.
- P(H) = , . untuk ketiga pintu, yang berarti bahwa sebelum pintu terbuka dan kambing terbuka, ada peluang yang sama untuk mobil berada di belakang salah satu dari mereka.
Kemungkinan dapat didefinisikan sebagai:
-
P(D|H), di mana kejadian D adalah bahwa Monty memilih pintu B dan tidak ada mobil di belakangnya. -
P(D|H)= 1/2 jika mobil berada di belakang pintu A - karena ada peluang 50% dia akan memilih pintu B dan 50% peluang dia memilih pintu C. -
P(D|H)= 0 jika mobil berada di belakang pintu B, karena ada peluang 0% bahwa ia akan memilih pintu B jika mobil berada di belakangnya. -
P(D|H)= 1 jika mobil berada di belakang C, dan Anda memilih A, ada kemungkinan 100% dia akan memilih pintu B.
Kami tertarik pada P(H|D) , yang merupakan peluang mobil berada di belakang pintu jika mobil tersebut menunjukkan seekor kambing di belakang salah satu pintu lainnya.
Dapat dilihat dari posterior, P(H|D) , bahwa beralih ke pintu C dari A akan meningkatkan kemungkinan menang.
Metropolis-Hastings
Sekarang, mari gabungkan semua yang telah kita bahas sejauh ini dan coba pahami cara kerja Metropolis-Hastings.
Metropolis-Hastings menggunakan teorema Bayes untuk mendapatkan distribusi posterior dari distribusi yang kompleks, dari mana pengambilan sampel secara langsung sulit dilakukan.
Bagaimana? Pada dasarnya, ini secara acak memilih sampel yang berbeda dari suatu ruang dan memeriksa apakah sampel baru lebih mungkin berasal dari posterior daripada sampel terakhir, karena kita melihat rasio probabilitas, P(B) dalam persamaan (1), dapatkan dibatalkan:
P(penerimaan) = ( P(Sampel baru) * Kemungkinan sampel baru) / (P(Sampel lama) * Kemungkinan sampel lama)
"Kemungkinan" dari setiap sampel baru ditentukan oleh fungsi f . Itu sebabnya f harus proporsional dengan posterior yang ingin kita sampel.
Untuk memutuskan apakah akan diterima atau ditolak, rasio berikut harus dihitung untuk setiap ' baru yang diusulkan:
Dimana adalah sampel lama, P(D| θ) adalah kemungkinan sampel .
Mari kita gunakan contoh untuk memahami ini dengan lebih baik. Katakanlah Anda memiliki data tetapi Anda ingin mengetahui distribusi normal yang sesuai, jadi:
X ~ N(rata-rata, std)
Sekarang kita perlu mendefinisikan prior untuk mean dan std keduanya. Untuk mempermudah, kita asumsikan keduanya mengikuti distribusi normal dengan mean 1 dan std 2:
Rata-rata ~ N(1, 2)
std ~ N(1, 2)
Sekarang, mari kita buat beberapa data dan asumsikan rata-rata dan std yang sebenarnya masing-masing adalah 0,5 dan 1,2.
import numpy as np import matplotlib.pyplot as plt import scipy.stats as st meanX = 1.5 stdX = 1.2 X = np.random.normal(meanX, stdX, size = 1000) _ = plt.hist(X, bins = 50)PyMC3
Pertama-tama mari kita gunakan pustaka yang disebut PyMC3 untuk memodelkan data dan menemukan distribusi posterior untuk mean dan std.
import pymc3 as pm with pm.Model() as model: mean = pm.Normal("mean", mu = 1, sigma = 2) std = pm.Normal("std", mu = 1, sigma = 2) x = pm.Normal("X", mu = mean, sigma = std, observed = X) step = pm.Metropolis() trace = pm.sample(5000, step = step)Mari kita bahas kodenya.
Pertama, kita mendefinisikan prior untuk mean dan std, yaitu, normal dengan mean 1 dan std 2.
x = pm.Normal(“X”, mu = mean, sigma = std, teramati = X)
Di baris ini, kita mendefinisikan variabel yang kita minati; dibutuhkan mean dan std yang kita definisikan sebelumnya, juga mengambil nilai observasi yang kita hitung sebelumnya.
Mari kita lihat hasilnya:
_ = plt.hist(trace['std'], bins = 50, label = "std") _ = plt.hist(trace['mean'], bins = 50, label = "mean") _ = plt.legend()Std berpusat di sekitar 1,2, dan rata-rata berada di 1,55 - cukup dekat!
Sekarang mari kita lakukan dari awal untuk memahami Metropolis-Hastings.
Dari awal
Membuat Proposal
Pertama, mari kita pahami apa yang dilakukan Metropolis-Hastings. Sebelumnya di artikel ini, kami mengatakan, "Metropolis-Hastings secara acak memilih sampel yang berbeda dari suatu ruang," tetapi bagaimana cara mengetahui sampel mana yang harus dipilih?
Ia melakukannya dengan menggunakan distribusi proposal. Ini adalah distribusi normal yang berpusat pada sampel yang diterima saat ini dan memiliki STD 0,5. Di mana 0,5 adalah hyperparameter, kita dapat men-tweak; semakin banyak STD proposal, semakin jauh ia akan mencari dari sampel yang diterima saat ini. Mari kita kode ini.
Karena kita harus mencari mean dan std dari distribusi, fungsi ini akan mengambil mean yang diterima saat ini dan std yang diterima saat ini, dan mengembalikan proposal untuk keduanya.
def get_proposal(mean_current, std_current, proposal_width = 0.5): return np.random.normal(mean_current, proposal_width), \ np.random.normal(std_current, proposal_width)Menerima/Menolak Proposal
Sekarang, mari kita buat kode logika yang menerima atau menolak proposal. Ini memiliki dua bagian: sebelumnya dan kemungkinan .
Pertama, mari kita hitung probabilitas proposal yang datang dari sebelumnya:
def prior(mean, std, prior_mean, prior_std): return st.norm(prior_mean[0], prior_mean[1]).pdf(mean)* \ st.norm(prior_std[0], prior_std[1]).pdf(std)Itu hanya membutuhkan mean dan std dan menghitung seberapa besar kemungkinan mean dan std ini berasal dari distribusi sebelumnya yang kami definisikan.
Dalam menghitung kemungkinan, kami menghitung seberapa besar kemungkinan data yang kami lihat berasal dari distribusi yang diusulkan.
def likelihood(mean, std, data): return np.prod(st.norm(mean, std).pdf(X))Jadi untuk setiap titik data, kita kalikan probabilitas titik data tersebut berasal dari distribusi yang diusulkan.
Sekarang, kita perlu memanggil fungsi-fungsi ini untuk mean dan std saat ini dan untuk mean dan std yang diusulkan.
prior_current = prior(mean_current, std_current, prior_mean, prior_std) likelihood_current = likelihood(mean_current, std_current, data) prior_proposal = prior(mean_proposal, std_proposal, prior_mean, prior_std) likelihood_proposal = likelihood(mean_proposal, std_proposal, data)Seluruh kode:
def accept_proposal(mean_proposal, std_proposal, mean_current, \ std_current, prior_mean, prior_std, data): def prior(mean, std, prior_mean, prior_std): return st.norm(prior_mean[0], prior_mean[1]).pdf(mean)* \ st.norm(prior_std[0], prior_std[1]).pdf(std) def likelihood(mean, std, data): return np.prod(st.norm(mean, std).pdf(X)) prior_current = prior(mean_current, std_current, prior_mean, prior_std) likelihood_current = likelihood(mean_current, std_current, data) prior_proposal = prior(mean_proposal, std_proposal, prior_mean, prior_std) likelihood_proposal = likelihood(mean_proposal, std_proposal, data) return (prior_proposal * likelihood_proposal) / (prior_current * likelihood_current)Sekarang, mari kita buat fungsi terakhir yang akan mengikat semuanya dan menghasilkan sampel posterior yang kita butuhkan.
Menghasilkan Posterior
Sekarang, kita memanggil fungsi yang telah kita tulis di atas dan menghasilkan posterior!
def get_trace(data, samples = 5000): mean_prior = 1 std_prior = 2 mean_current = mean_prior std_current = std_prior trace = { "mean": [mean_current], "std": [std_current] } for i in tqdm(range(samples)): mean_proposal, std_proposal = get_proposal(mean_current, std_current) acceptance_prob = accept_proposal(mean_proposal, std_proposal, mean_current, \ std_current, [mean_prior, std_prior], \ [mean_prior, std_prior], data) if np.random.rand() < acceptance_prob: mean_current = mean_proposal std_current = std_proposal trace['mean'].append(mean_current) trace['std'].append(std_current) return traceRuang untuk Peningkatan
Log adalah teman Anda!
Ingat a * b = antilog(log(a) + log(b)) dan a / b = antilog(log(a) - log(b)).
Ini bermanfaat bagi kami karena kami akan berurusan dengan probabilitas yang sangat kecil, mengalikan yang akan menghasilkan nol, jadi kami lebih suka menambahkan log prob, masalah terpecahkan!
Jadi, kode kita sebelumnya menjadi:
def accept_proposal(mean_proposal, std_proposal, mean_current, \ std_current, prior_mean, prior_std, data): def prior(mean, std, prior_mean, prior_std): return st.norm(prior_mean[0], prior_mean[1]).logpdf(mean)+ \ st.norm(prior_std[0], prior_std[1]).logpdf(std) def likelihood(mean, std, data): return np.sum(st.norm(mean, std).logpdf(X)) prior_current = prior(mean_current, std_current, prior_mean, prior_std) likelihood_current = likelihood(mean_current, std_current, data) prior_proposal = prior(mean_proposal, std_proposal, prior_mean, prior_std) likelihood_proposal = likelihood(mean_proposal, std_proposal, data) return (prior_proposal + likelihood_proposal) - (prior_current + likelihood_current)Karena kami mengembalikan log probabilitas penerimaan:
if np.random.rand() < acceptance_prob:
Menjadi:
if math.log(np.random.rand()) < acceptance_prob:
Mari kita jalankan kode baru dan plot hasilnya.
_ = plt.hist(trace['std'], bins = 50, label = "std") _ = plt.hist(trace['mean'], bins = 50, label = "mean") _ = plt.legend()Seperti yang Anda lihat, std berpusat di 1,2, dan rata- rata di 1,5. Kita berhasil!
Bergerak kedepan
Sekarang, semoga Anda memahami cara kerja Metropolis-Hastings dan Anda mungkin bertanya-tanya di mana Anda dapat menggunakannya.
Nah, Metode Bayesian untuk Peretas adalah buku bagus yang menjelaskan pemrograman probabilistik, dan jika Anda ingin mempelajari lebih lanjut tentang teorema Bayes dan aplikasinya, Think Bayes adalah buku hebat karya Allen B. Downey.
Terima kasih telah membaca, dan saya harap artikel ini mendorong Anda untuk menemukan dunia statistik Bayesian yang menakjubkan.
