MCMC 方法:Metropolis-Hastings 和貝葉斯推理
已發表: 2022-03-11讓我們弄清楚基本定義:馬爾可夫鏈蒙特卡羅 (MCMC) 方法讓我們可以從分佈中計算樣本,即使我們無法計算它。
這是什麼意思? 讓我們回過頭來談談蒙特卡洛抽樣。
蒙特卡洛抽樣
什麼是蒙特卡羅方法?
“蒙特卡洛方法或蒙特卡洛實驗是一類廣泛的計算算法,它依賴於重複隨機抽樣來獲得數值結果。” (維基百科)
讓我們分解一下。
示例 1:面積估計
想像一下你有一個不規則的形狀,如下圖所示:
你的任務是確定這個形狀所包圍的區域。 您可以使用的一種方法是在形狀中製作小正方形,計算正方形,這將為您提供一個非常準確的面積近似值。 然而,這既困難又耗時。
蒙特卡洛採樣來救援!
首先,我們在形狀周圍畫一個已知面積的大正方形,例如 50 平方厘米。 現在我們“懸掛”這個正方形並開始隨機向該形狀投擲飛鏢。
接下來,我們計算矩形中的省道總數和我們感興趣的形狀中的省道數。假設使用的“省道”總數為 100,其中 22 個最終在形狀內。 現在可以通過簡單的公式計算面積:
形狀面積=正方形面積*(形狀中的飛鏢數)/(正方形中的飛鏢數)
所以,在我們的例子中,這歸結為:
形狀面積 = 50 * 22/100 = 11 cm2
如果我們將“飛鏢”的數量乘以 10 倍,這個近似值將非常接近真實答案:
形狀面積 = 50 * 280/1000 = 14 cm2
這就是我們如何通過使用蒙特卡羅抽樣來分解複雜的任務,就像上面給出的那樣。
大數定律
我們投的飛鏢越多,面積近似值越接近,這是因為大數定律:
“大數定律是描述多次執行相同實驗的結果的定理。 根據規律,大量試驗得到的結果的平均值應該接近預期值,並且隨著試驗次數的增加而趨於接近。”
這將我們帶到下一個例子,著名的蒙蒂霍爾問題。
示例 2:蒙蒂霍爾問題
蒙蒂霍爾問題是一個非常有名的腦筋急轉彎:
“一共有三扇門,一扇後面是一輛車,其他的後面是一隻山羊。 你選擇一扇門,主人打開另一扇門,告訴你門後有一隻山羊。 然後他問你是否想改變你的決定。 你? 為什麼? 為什麼不?”
您首先想到的是,無論您是否切換,獲勝的機會都是平等的,但事實並非如此。 讓我們製作一個簡單的流程圖來演示。
假設汽車在 3 號門後面:
因此,如果你切換,你贏了 ⅔ 次,如果你不切換,你只贏了 ⅓ 次。
讓我們通過採樣來解決這個問題。
wins = [] for i in range(int(10e6)): car_door = assign_car_door() choice = random.randint(0, 2) opened_door = assign_door_to_open(car_door) did_he_win = win_or_lose(choice, car_door, opened_door, switch = False) wins.append(did_he_win) print(sum(wins)/len(wins)) assign_car_door()函數只是一個隨機數生成器,用於選擇門 0、1 或 2,在門後有汽車。 使用assign_door_to_open選擇一扇門,門後面有一隻山羊,但不是您選擇的門,主機打開它。 win_or_lose返回true或false ,表示您是否贏得了汽車,它需要一個布爾“開關”,表示您是否切換了門。
讓我們運行這個模擬 1000 萬次:
- 不切換中獎概率:0.334134
- 如果你切換獲勝的概率:0.667255
這與流程圖給我們的答案非常接近。
事實上,我們運行這個模擬的次數越多,答案就越接近真實值,從而驗證了大數定律:
從這張表中也可以看出:
| 模擬運行 | 換手後中獎概率 | 如果您不切換,獲勝的概率 |
| 10 | 0.6 | 0.2 |
| 10^2 | 0.63 | 0.33 |
| 10^3 | 0.661 | 0.333 |
| 10^4 | 0.6683 | 0.3236 |
| 10^5 | 0.66762 | 0.33171 |
| 10^6 | 0.667255 | 0.334134 |
| 10^7 | 0.6668756 | 0.3332821 |
貝葉斯思維方式
“頻率學家,被稱為統計學的更經典版本,假設概率是事件的長期頻率(因此被授予標題)。”
“貝葉斯統計是統計領域的一種理論,它基於概率的貝葉斯解釋,其中概率表示對事件的相信程度。 信念程度可能基於對事件的先驗知識,例如先前實驗的結果,或基於對事件的個人信念。” - 來自黑客的概率編程和貝葉斯方法
這是什麼意思?
在頻率論者的思維方式中,我們從長遠角度看待概率。 當一位常客說發生車禍的可能性為 0.001% 時,這意味著,如果我們考慮無限次的汽車旅行,其中 0.001% 的車禍將以車禍告終。
貝葉斯的心態是不同的,因為我們從一個先驗開始,一個信念。 如果我們談論 0 的信念,這意味著您的信念是事件永遠不會發生; 相反,信念為 1 意味著您確信它會發生。
然後,一旦我們開始觀察數據,我們就會更新這個信念以考慮數據。 我們如何做到這一點? 通過使用貝葉斯定理。
貝葉斯定理
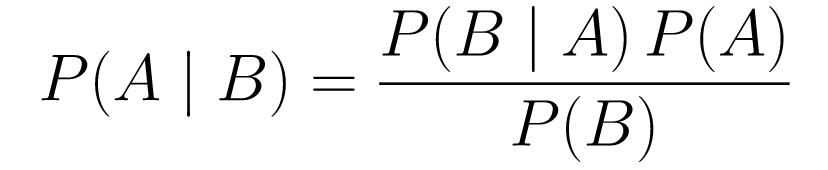 ....(1)
....(1)讓我們分解一下。
-
P(A | B)給出了給定事件 B 的事件 A 的概率。這是後驗概率,B 是我們觀察到的數據,所以考慮到我們觀察到的數據,我們本質上是在說事件發生的概率是多少。 -
P(A)是先驗的,我們相信事件 A 會發生。 -
P(B | A)是可能性,假設 A 為真,我們觀察數據的概率是多少。
讓我們看一個例子,癌症篩查測試。
癌症的概率
假設一位患者去做乳房 X 光檢查,而乳房 X 光檢查結果呈陽性。 患者實際上患有癌症的概率是多少?
讓我們定義概率:
- 1% 的女性患有乳腺癌。
- 乳房 X 線照片在 80% 的時間裡檢測到癌症實際上存在。
- 9.6% 的乳房 X 線照片錯誤地報告您患有癌症,而實際上您並沒有患上癌症。
因此,如果您說如果乳房 X 光檢查結果呈陽性,則意味著您有 80% 的機會患有癌症,那將是錯誤的。 您不會考慮到患癌症是一種罕見的事件,即只有 1% 的女性患有乳腺癌。 我們需要將此作為先決條件,這就是貝葉斯定理髮揮作用的地方:
P(C+ | T+) =(P(T+|C+)*P(C+))/P(T+)
-
P(C+ | T+):這是癌症存在的概率,假設測試是陽性的,這就是我們感興趣的。 -
P(T+ | C+):這是測試為陽性的概率,假設存在癌症,如上所述,這等於 80% = 0.8。 -
P(C+):這是先驗概率,一個人患癌症的概率,等於 1% = 0.01。 -
P(T+):這是測試為陽性的概率,無論如何,它有兩個分量: P(T+) = P(T+|C-) P(C-)+P(T+|C+) P (C+) -
P(T+ | C-):這是檢測結果呈陽性但沒有癌症的概率,由 0.096 給出。 -
P(C-):這是沒有患癌症的概率,因為患癌症的概率是 1%,這等於 99% = 0.99。 -
P(T+ | C+):這是檢測結果呈陽性的概率,假設您患有癌症,這等於 80% = 0.8。 -
P(C+):這是患癌症的概率,等於 1% = 0.01。
將所有這些代入原始公式:
因此,鑑於乳房 X 光檢查結果呈陽性,患者患癌症的機率為 7.76%。 起初可能看起來很奇怪,但它是有道理的。 該測試給出了 9.6% 的假陽性(相當高),因此在給定的人群中會有很多假陽性。 對於一種罕見的疾病,大多數陽性檢測結果都是錯誤的。
現在讓我們重新審視蒙蒂霍爾問題並使用貝葉斯定理解決它。
蒙蒂霍爾問題
先驗可以定義為:
- 假設您一開始選擇門 A 作為您的選擇。
- P(H) = ⅓, ⅓。 ⅓ 對於所有三個門,這意味著在門打開並且山羊露出之前,汽車在其中任何一個後面的機會均等。
可能性可以定義為:
-
P(D|H),其中事件 D 是蒙蒂選擇了門 B 並且後面沒有車。 - 如果汽車在門 A 後面,則
P(D|H)= 1/2 - 因為他有 50% 的機會選擇 B 門,而他有 50% 的機會選擇門 C。 - 如果汽車在門 B 後面,則
P(D|H)= 0,因為如果汽車在門 B 後面,他有 0% 的機會選擇門 B。 -
P(D|H)= 1 如果汽車在 C 後面,而你選擇 A,那麼他有 100% 的概率會選擇 B 門。
我們對P(H|D)感興趣,這是汽車在門後面的概率,因為它向我們展示了一隻山羊在其他門後面。
從後驗P(H|D)可以看出,從 A 切換到門 C 會增加獲勝的概率。
大都會-黑斯廷斯
現在,讓我們結合目前為止介紹的所有內容,並嘗試了解 Metropolis-Hastings 的工作原理。
Metropolis-Hastings 使用貝葉斯定理獲得複雜分佈的後驗分佈,很難從中直接採樣。
如何? 本質上,它從一個空間中隨機選擇不同的樣本並檢查新樣本是否比上一個樣本更有可能來自後驗,因為我們正在查看等式(1)中的概率比 P(B),得到取消:
P(acceptance) = ( P(newSample) * 新樣本的可能性) / (P(oldSample) * 舊樣本的可能性)

每個新樣本的“可能性”由函數f決定。 這就是為什麼f必須與我們要從中採樣的後驗成正比的原因。
為了決定是接受還是拒絕 θ',必須為每個新提議的 θ' 計算以下比率:
其中 θ 是舊樣本, P(D| θ)是樣本 θ 的似然性。
讓我們用一個例子來更好地理解這一點。 假設您有數據,但您想找出適合它的正態分佈,所以:
X ~ N(平均,標準)
現在我們需要定義均值和標準的先驗。 為簡單起見,我們假設兩者都服從均值 1 和標準差 2 的正態分佈:
均值 ~ N(1, 2)
標準~N(1, 2)
現在,讓我們生成一些數據並假設真實均值和標準差分別為 0.5 和 1.2。
import numpy as np import matplotlib.pyplot as plt import scipy.stats as st meanX = 1.5 stdX = 1.2 X = np.random.normal(meanX, stdX, size = 1000) _ = plt.hist(X, bins = 50)PyMC3
讓我們首先使用一個名為PyMC3的庫來對數據進行建模並找到均值和標準差的後驗分佈。
import pymc3 as pm with pm.Model() as model: mean = pm.Normal("mean", mu = 1, sigma = 2) std = pm.Normal("std", mu = 1, sigma = 2) x = pm.Normal("X", mu = mean, sigma = std, observed = X) step = pm.Metropolis() trace = pm.sample(5000, step = step)讓我們回顧一下代碼。
首先,我們定義均值和標準差的先驗,即均值 1 和標準差 2 的法線。
x = pm.Normal(“X”,mu = mean,sigma = std,observed = X)
在這一行中,我們定義了我們感興趣的變量; 它採用我們之前定義的平均值和標準差,它還採用我們之前計算的觀察值。
讓我們看看結果:
_ = plt.hist(trace['std'], bins = 50, label = "std") _ = plt.hist(trace['mean'], bins = 50, label = "mean") _ = plt.legend()標準以 1.2 為中心,平均值為 1.55 - 非常接近!
現在讓我們從頭開始了解 Metropolis-Hastings。
從頭開始
生成提案
首先,讓我們了解 Metropolis-Hastings 是做什麼的。 在本文前面,我們說過, “Metropolis-Hastings 從一個空間中隨機選擇不同的樣本”,但它如何知道要選擇哪個樣本呢?
它使用提案分佈來做到這一點。 它是一個以當前接受的樣本為中心的正態分佈,STD 為 0.5。 其中 0.5 是超參數,我們可以調整; 提案的 STD 越多,它將從當前接受的樣本中搜索得越遠。 讓我們對此進行編碼。
由於我們必須找到分佈的均值和標準差,因此該函數將採用當前接受的均值和當前接受的標準差,並返回兩者的建議。
def get_proposal(mean_current, std_current, proposal_width = 0.5): return np.random.normal(mean_current, proposal_width), \ np.random.normal(std_current, proposal_width)接受/拒絕提案
現在,讓我們編寫接受或拒絕提案的邏輯。 它有兩部分:先驗和可能性。
首先,讓我們計算提案來自先驗的概率:
def prior(mean, std, prior_mean, prior_std): return st.norm(prior_mean[0], prior_mean[1]).pdf(mean)* \ st.norm(prior_std[0], prior_std[1]).pdf(std)它只取均值和標準差併計算該均值和標準差來自我們定義的先驗分佈的可能性。
在計算可能性時,我們計算我們看到的數據來自建議分佈的可能性。
def likelihood(mean, std, data): return np.prod(st.norm(mean, std).pdf(X))因此,對於每個數據點,我們乘以該數據點來自建議分佈的概率。
現在,我們需要為當前的均值和標準以及建議的均值和標準調用這些函數。
prior_current = prior(mean_current, std_current, prior_mean, prior_std) likelihood_current = likelihood(mean_current, std_current, data) prior_proposal = prior(mean_proposal, std_proposal, prior_mean, prior_std) likelihood_proposal = likelihood(mean_proposal, std_proposal, data)整個代碼:
def accept_proposal(mean_proposal, std_proposal, mean_current, \ std_current, prior_mean, prior_std, data): def prior(mean, std, prior_mean, prior_std): return st.norm(prior_mean[0], prior_mean[1]).pdf(mean)* \ st.norm(prior_std[0], prior_std[1]).pdf(std) def likelihood(mean, std, data): return np.prod(st.norm(mean, std).pdf(X)) prior_current = prior(mean_current, std_current, prior_mean, prior_std) likelihood_current = likelihood(mean_current, std_current, data) prior_proposal = prior(mean_proposal, std_proposal, prior_mean, prior_std) likelihood_proposal = likelihood(mean_proposal, std_proposal, data) return (prior_proposal * likelihood_proposal) / (prior_current * likelihood_current)現在,讓我們創建最終函數,將所有內容聯繫在一起並生成我們需要的後驗樣本。
生成後驗
現在,我們調用上面編寫的函數並生成後驗!
def get_trace(data, samples = 5000): mean_prior = 1 std_prior = 2 mean_current = mean_prior std_current = std_prior trace = { "mean": [mean_current], "std": [std_current] } for i in tqdm(range(samples)): mean_proposal, std_proposal = get_proposal(mean_current, std_current) acceptance_prob = accept_proposal(mean_proposal, std_proposal, mean_current, \ std_current, [mean_prior, std_prior], \ [mean_prior, std_prior], data) if np.random.rand() < acceptance_prob: mean_current = mean_proposal std_current = std_proposal trace['mean'].append(mean_current) trace['std'].append(std_current) return trace改進空間
日誌是你的朋友!
回想一下a * b = antilog(log(a) + log(b))和a / b = antilog(log(a) - log(b)).
這對我們有利,因為我們將處理非常小的概率,相乘將導致零,所以我們寧願添加對數概率,問題解決了!
所以,我們之前的代碼變成了:
def accept_proposal(mean_proposal, std_proposal, mean_current, \ std_current, prior_mean, prior_std, data): def prior(mean, std, prior_mean, prior_std): return st.norm(prior_mean[0], prior_mean[1]).logpdf(mean)+ \ st.norm(prior_std[0], prior_std[1]).logpdf(std) def likelihood(mean, std, data): return np.sum(st.norm(mean, std).logpdf(X)) prior_current = prior(mean_current, std_current, prior_mean, prior_std) likelihood_current = likelihood(mean_current, std_current, data) prior_proposal = prior(mean_proposal, std_proposal, prior_mean, prior_std) likelihood_proposal = likelihood(mean_proposal, std_proposal, data) return (prior_proposal + likelihood_proposal) - (prior_current + likelihood_current)因為我們要返回接受概率的對數:
if np.random.rand() < acceptance_prob:
變成:
if math.log(np.random.rand()) < acceptance_prob:
讓我們運行新代碼並繪製結果。
_ = plt.hist(trace['std'], bins = 50, label = "std") _ = plt.hist(trace['mean'], bins = 50, label = "mean") _ = plt.legend()如您所見, std以 1.2 為中心,平均值以 1.5 為中心。 我們做到了!
向前進
到目前為止,您希望了解 Metropolis-Hastings 的工作原理,並且您可能想知道在哪裡可以使用它。
好吧, Bayesian Methods for Hackers是一本解釋概率編程的優秀書籍,如果您想了解更多關於貝葉斯定理及其應用的信息, Think Bayes是 Allen B. Downey 的一本好書。
感謝您的閱讀,我希望這篇文章能鼓勵您探索貝葉斯統計的奇妙世界。
