Méthodes MCMC : Metropolis-Hastings et inférence bayésienne
Publié: 2022-03-11Éliminons la définition de base : les méthodes de Markov Chain Monte Carlo (MCMC) nous permettent de calculer des échantillons à partir d'une distribution même si nous ne pouvons pas la calculer.
Qu'est-ce que ça veut dire? Revenons en arrière et parlons de Monte Carlo Sampling.
Échantillonnage de Monte-Carlo
Que sont les méthodes de Monte Carlo ?
"Les méthodes de Monte Carlo, ou expériences de Monte Carlo, sont une large classe d'algorithmes de calcul qui reposent sur un échantillonnage aléatoire répété pour obtenir des résultats numériques." (Wikipédia)
Décomposons cela.
Exemple 1 : Estimation de superficie
Imaginez que vous avez une forme irrégulière, comme la forme présentée ci-dessous :
Et vous êtes chargé de déterminer la zone délimitée par cette forme. L'une des méthodes que vous pouvez utiliser consiste à créer de petits carrés dans la forme, à compter les carrés, et cela vous donnera une approximation assez précise de la zone. Cependant, cela est difficile et prend du temps.
L'échantillonnage de Monte Carlo à la rescousse !
D'abord, on dessine un grand carré d'une surface connue autour de la forme, par exemple de 50 cm2. Maintenant, nous "suspendons" ce carré et commençons à lancer des fléchettes au hasard sur la forme.
Ensuite, nous comptons le nombre total de fléchettes dans le rectangle et le nombre de fléchettes dans la forme qui nous intéresse. Supposons que le nombre total de "fléchettes" utilisées était de 100 et que 22 d'entre elles se sont retrouvées dans la forme. Maintenant, la surface peut être calculée par la formule simple :
aire de la forme = aire du carré *(nombre de pinces dans la forme) / (nombre de pinces dans le carré)
Donc, dans notre cas, cela revient à :
aire de forme = 50 * 22/100 = 11 cm2
Si nous multiplions le nombre de "fléchettes" par un facteur de 10, cette approximation devient très proche de la vraie réponse :
aire de forme = 50 * 280/1000 = 14 cm2
C'est ainsi que nous décomposons des tâches compliquées, comme celle donnée ci-dessus, en utilisant l'échantillonnage de Monte Carlo.
La loi des grands nombres
L'approximation de la zone était plus proche plus nous lançions de fléchettes, et c'est à cause de la loi des grands nombres :
« La loi des grands nombres est un théorème qui décrit le résultat de la réalisation de la même expérience un grand nombre de fois. Selon la loi, la moyenne des résultats obtenus à partir d'un grand nombre d'essais doit être proche de la valeur attendue, et aura tendance à se rapprocher au fur et à mesure que d'autres essais sont effectués.
Cela nous amène à notre exemple suivant, le fameux problème de Monty Hall.
Exemple 2 : Le problème de Monty Hall
Le problème de Monty Hall est un casse-tête très célèbre :
"Il y a trois portes, l'une a une voiture derrière, les autres ont une chèvre derrière elles. Vous choisissez une porte, l'hôte ouvre une autre porte et vous montre qu'il y a une chèvre derrière. Il vous demande alors si vous souhaitez revenir sur votre décision. Est-ce que tu? Pourquoi? Pourquoi pas?"
La première chose qui vous vient à l'esprit est que les chances de gagner sont égales, que vous changiez ou non, mais ce n'est pas vrai. Faisons un organigramme simple pour démontrer la même chose.
En supposant que la voiture se trouve derrière la porte 3 :
Ainsi, si vous changez, vous gagnez ⅔ fois, et si vous ne changez pas, vous ne gagnez que ⅓ fois.
Résolvons cela en utilisant l'échantillonnage.
wins = [] for i in range(int(10e6)): car_door = assign_car_door() choice = random.randint(0, 2) opened_door = assign_door_to_open(car_door) did_he_win = win_or_lose(choice, car_door, opened_door, switch = False) wins.append(did_he_win) print(sum(wins)/len(wins)) La fonction assign_car_door() est juste un générateur de nombres aléatoires qui sélectionne une porte 0, 1 ou 2 derrière laquelle se trouve une voiture. L'utilisation assign_door_to_open sélectionne une porte qui a une chèvre derrière elle et qui n'est pas celle que vous avez sélectionnée, et l'hôte l'ouvre. win_or_lose renvoie true ou false , indiquant si vous avez gagné la voiture ou non, il faut un "commutateur" booléen qui indique si vous avez commuté la porte ou non.
Exécutons cette simulation 10 millions de fois :
- Probabilité de gagner si vous ne changez pas : 0,334134
- Probabilité de gagner si vous changez : 0,667255
C'est très proche des réponses que l'organigramme nous a données.
En fait, plus nous exécutons cette simulation, plus la réponse se rapproche de la vraie valeur, validant ainsi la loi des grands nombres :
On peut voir la même chose sur ce tableau :
| Simulations exécutées | Probabilité de gagner si vous changez | Probabilité de gagner si vous ne changez pas |
| dix | 0,6 | 0,2 |
| 10^2 | 0,63 | 0,33 |
| 10^3 | 0,661 | 0,333 |
| 10^4 | 0,6683 | 0,3236 |
| 10^5 | 0,66762 | 0,33171 |
| 10^6 | 0,667255 | 0,334134 |
| 10^7 | 0,6668756 | 0.3332821 |
La pensée bayésienne
"Fréquentiste, connu comme la version la plus classique des statistiques, suppose que la probabilité est la fréquence à long terme des événements (d'où le titre accordé)."
« La statistique bayésienne est une théorie dans le domaine des statistiques basée sur l'interprétation bayésienne de la probabilité où la probabilité exprime un degré de croyance en un événement. Le degré de croyance peut être basé sur une connaissance préalable de l'événement, comme les résultats d'expériences précédentes, ou sur des croyances personnelles à propos de l'événement. - de la programmation probabiliste et des méthodes bayésiennes pour les hackers
Qu'est-ce que ça veut dire?
Dans le mode de pensée fréquentiste, nous regardons les probabilités à long terme. Lorsqu'un fréquentiste dit qu'il y a 0,001 % de chances qu'un accident de voiture se produise, cela signifie que si l'on considère des trajets en voiture infinis, 0,001 % d'entre eux se termineront par un accident.
Un état d'esprit bayésien est différent, car nous commençons par un préalable, une croyance. Si nous parlons d'une croyance de 0, cela signifie que votre croyance est que l'événement ne se produira jamais ; à l'inverse, une croyance de 1 signifie que vous êtes sûr que cela se produira.
Ensuite, une fois que nous commençons à observer les données, nous mettons à jour cette croyance pour prendre en considération les données. Comment faisons-nous cela? En utilisant le théorème de Bayes.
Théorème de Bayes
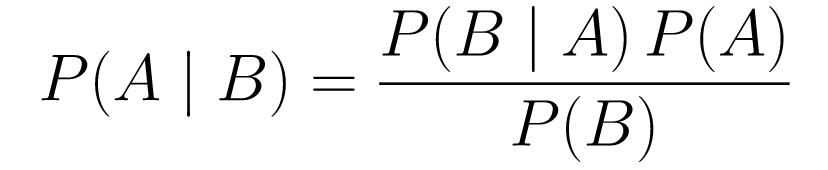 ....(1)
....(1)Décomposons-le.
-
P(A | B)nous donne la probabilité de l'événement A étant donné l'événement B. C'est le postérieur, B est les données que nous avons observées, donc nous disons essentiellement quelle est la probabilité qu'un événement se produise, compte tenu des données que nous avons observées. -
P(A)est le prior, notre croyance que l'événement A se produira. -
P(B | A)est la vraisemblance, quelle est la probabilité que nous observions les données étant donné que A est vraie.
Prenons un exemple, le test de dépistage du cancer.
Probabilité de cancer
Disons qu'une patiente va passer une mammographie et que la mammographie est positive. Quelle est la probabilité que le patient ait réellement un cancer ?
Définissons les probabilités :
- 1% des femmes ont un cancer du sein.
- Les mammographies détectent le cancer 80 % du temps lorsqu'il est réellement présent.
- 9,6 % des mammographies signalent à tort que vous avez un cancer alors que vous n'en avez pas.
Donc, si vous disiez que si une mammographie est positive, ce qui signifie qu'il y a 80 % de chances que vous ayez un cancer, ce serait faux. Vous ne prendriez pas en considération le fait qu'avoir un cancer est un événement rare, c'est-à-dire que seulement 1 % des femmes ont un cancer du sein. Nous devons prendre cela comme avant, et c'est là que le théorème de Bayes entre en jeu :
P(C+ | T+) =(P(T+|C+)*P(C+))/P(T+)
-
P(C+ | T+): C'est la probabilité qu'il y ait un cancer, étant donné que le test était positif, c'est ce qui nous intéresse. -
P(T+ | C+): C'est la probabilité que le test soit positif, étant donné qu'il y a un cancer, ceci, comme discuté ci-dessus est égal à 80% = 0,8. -
P(C+): C'est la probabilité a priori, la probabilité qu'un individu ait un cancer, qui est égale à 1% = 0,01. -
P(T+): C'est la probabilité que le test soit positif, quoi qu'il arrive, il a donc deux composantes : P(T+) = P(T+|C-) P(C-)+P(T+|C+) P (C+) -
P(T+ | C-): C'est la probabilité que le test soit revenu positif mais qu'il n'y ait pas de cancer, elle est donnée par 0,096. -
P(C-): C'est la probabilité de ne pas avoir de cancer puisque la probabilité d'avoir un cancer est de 1%, ceci est égal à 99% = 0,99. -
P(T+ | C+): C'est la probabilité que le test revienne positif, sachant que vous avez un cancer, c'est égal à 80% = 0,8. -
P(C+): C'est la probabilité d'avoir un cancer, qui est égale à 1% = 0,01.
Brancher tout cela dans la formule originale :
Donc, étant donné que la mammographie est revenue positive, il y a 7,76 % de chances que la patiente ait un cancer. Cela peut sembler étrange au premier abord, mais cela a du sens. Le test donne un faux positif 9,6 % du temps (assez élevé), il y aura donc beaucoup de faux positifs dans une population donnée. Pour une maladie rare, la plupart des résultats de test positifs seront erronés.

Reprenons maintenant le problème de Monty Hall et résolvons-le en utilisant le théorème de Bayes.
Problème de Monty Hall
Les a priori peuvent être définis comme :
- Supposons que vous choisissiez la porte A comme choix au début.
- P(H) = ⅓, ⅓. ⅓ pour les trois portes, ce qui signifie qu'avant que la porte ne soit ouverte et que la chèvre ne soit révélée, il y avait une chance égale que la voiture soit derrière l'une d'entre elles.
La vraisemblance peut être définie comme :
-
P(D|H), où l'événement D est que Monty choisit la porte B et qu'il n'y a pas de voiture derrière. -
P(D|H)= 1/2 si la voiture est derrière la porte A - puisqu'il y a 50% de chance qu'il choisisse la porte B et 50% de chance qu'il choisisse la porte C. -
P(D|H)= 0 si la voiture est derrière la porte B, puisqu'il y a 0% de chance qu'il choisisse la porte B si la voiture est derrière. -
P(D|H)= 1 si la voiture est derrière C, et que vous choisissez A, il y a 100% de probabilité qu'il choisisse la porte B.
On s'intéresse à P(H|D) , qui est la probabilité que la voiture soit derrière une porte sachant qu'elle nous montre une chèvre derrière une des autres portes.
On peut voir à partir du postérieur, P(H|D) , que passer à la porte C depuis A augmentera la probabilité de gagner.
Métropolis-Hastings
Maintenant, combinons tout ce que nous avons couvert jusqu'à présent et essayons de comprendre le fonctionnement de Metropolis-Hastings.
Metropolis-Hastings utilise le théorème de Bayes pour obtenir la distribution a posteriori d'une distribution complexe, à partir de laquelle l'échantillonnage direct est difficile.
Comment? Essentiellement, il sélectionne au hasard différents échantillons d'un espace et vérifie si le nouvel échantillon est plus susceptible d'être du postérieur que le dernier échantillon, puisque nous examinons le rapport des probabilités, P (B) dans l'équation (1), obtient annulé :
P(acceptation) = ( P(newSample) * Probabilité du nouvel échantillon) / (P(oldSample) * Probabilité de l'ancien échantillon)
La « vraisemblance » de chaque nouvel échantillon est décidée par la fonction f . C'est pourquoi f doit être proportionnel à la postérieure à partir de laquelle nous voulons échantillonner.
Pour décider si θ′ doit être accepté ou rejeté, le rapport suivant doit être calculé pour chaque nouveau θ' proposé :
Où θ est l'ancien échantillon, P(D| θ) est la vraisemblance de l'échantillon θ.
Prenons un exemple pour mieux comprendre cela. Disons que vous avez des données mais que vous voulez trouver la distribution normale qui leur convient, donc :
X ~ N (moyenne, std)
Maintenant, nous devons définir les priors pour la moyenne et std à la fois. Pour simplifier, nous supposerons que les deux suivent une distribution normale avec moyenne 1 et std 2 :
Moyenne ~ N(1, 2)
type ~ N(1, 2)
Maintenant, générons des données et supposons que la vraie moyenne et la norme sont respectivement de 0,5 et 1,2.
import numpy as np import matplotlib.pyplot as plt import scipy.stats as st meanX = 1.5 stdX = 1.2 X = np.random.normal(meanX, stdX, size = 1000) _ = plt.hist(X, bins = 50)PyMC3
Utilisons d'abord une bibliothèque appelée PyMC3 pour modéliser les données et trouver la distribution postérieure pour la moyenne et std.
import pymc3 as pm with pm.Model() as model: mean = pm.Normal("mean", mu = 1, sigma = 2) std = pm.Normal("std", mu = 1, sigma = 2) x = pm.Normal("X", mu = mean, sigma = std, observed = X) step = pm.Metropolis() trace = pm.sample(5000, step = step)Passons en revue le code.
Tout d'abord, nous définissons l'a priori pour moyenne et std, c'est-à-dire une normale avec moyenne 1 et std 2.
x = pm.Normal("X", mu = moyenne, sigma = std, observé = X)
Dans cette ligne, nous définissons la variable qui nous intéresse ; il prend la moyenne et le std que nous avons définis plus tôt, il prend également les valeurs observées que nous avons calculées plus tôt.
Regardons les résultats :
_ = plt.hist(trace['std'], bins = 50, label = "std") _ = plt.hist(trace['mean'], bins = 50, label = "mean") _ = plt.legend()La norme est centrée autour de 1,2 et la moyenne est à 1,55 - assez proche !
Partons maintenant de zéro pour comprendre Metropolis-Hastings.
De zéro
Génération d'une proposition
Voyons d'abord ce que fait Metropolis-Hastings. Plus tôt dans cet article, nous avons dit : « Metropolis-Hastings sélectionne au hasard différents échantillons d'un espace », mais comment sait-il quel échantillon sélectionner ?
Il le fait en utilisant la distribution de proposition. Il s'agit d'une distribution normale centrée sur l'échantillon actuellement accepté et a un STD de 0,5. Où 0,5 est un hyperparamètre, nous pouvons modifier ; plus le STD de la proposition est élevé, plus la recherche s'éloignera de l'échantillon actuellement accepté. Codons ça.
Puisque nous devons trouver la moyenne et la norme de la distribution, cette fonction prendra la moyenne et la norme actuellement acceptées et renverra des propositions pour les deux.
def get_proposal(mean_current, std_current, proposal_width = 0.5): return np.random.normal(mean_current, proposal_width), \ np.random.normal(std_current, proposal_width)Accepter/rejeter une proposition
Maintenant, codons la logique qui accepte ou rejette la proposition. Il comporte deux parties : l'a priori et la vraisemblance .
Tout d'abord, calculons la probabilité que la proposition provienne de l'a priori :
def prior(mean, std, prior_mean, prior_std): return st.norm(prior_mean[0], prior_mean[1]).pdf(mean)* \ st.norm(prior_std[0], prior_std[1]).pdf(std)Il prend simplement la moyenne et la norme et calcule la probabilité que cette moyenne et cette norme proviennent de la distribution antérieure que nous avons définie.
En calculant la probabilité, nous calculons la probabilité que les données que nous avons vues proviennent de la distribution proposée.
def likelihood(mean, std, data): return np.prod(st.norm(mean, std).pdf(X))Ainsi, pour chaque point de données, nous multiplions la probabilité que ce point de données provienne de la distribution proposée.
Maintenant, nous devons appeler ces fonctions pour la moyenne et std actuelles et pour la moyenne et std proposées.
prior_current = prior(mean_current, std_current, prior_mean, prior_std) likelihood_current = likelihood(mean_current, std_current, data) prior_proposal = prior(mean_proposal, std_proposal, prior_mean, prior_std) likelihood_proposal = likelihood(mean_proposal, std_proposal, data)Le code entier :
def accept_proposal(mean_proposal, std_proposal, mean_current, \ std_current, prior_mean, prior_std, data): def prior(mean, std, prior_mean, prior_std): return st.norm(prior_mean[0], prior_mean[1]).pdf(mean)* \ st.norm(prior_std[0], prior_std[1]).pdf(std) def likelihood(mean, std, data): return np.prod(st.norm(mean, std).pdf(X)) prior_current = prior(mean_current, std_current, prior_mean, prior_std) likelihood_current = likelihood(mean_current, std_current, data) prior_proposal = prior(mean_proposal, std_proposal, prior_mean, prior_std) likelihood_proposal = likelihood(mean_proposal, std_proposal, data) return (prior_proposal * likelihood_proposal) / (prior_current * likelihood_current)Maintenant, créons la fonction finale qui liera tout et générera les échantillons postérieurs dont nous avons besoin.
Génération du postérieur
Maintenant, nous appelons les fonctions que nous avons écrites ci-dessus et générons la suite !
def get_trace(data, samples = 5000): mean_prior = 1 std_prior = 2 mean_current = mean_prior std_current = std_prior trace = { "mean": [mean_current], "std": [std_current] } for i in tqdm(range(samples)): mean_proposal, std_proposal = get_proposal(mean_current, std_current) acceptance_prob = accept_proposal(mean_proposal, std_proposal, mean_current, \ std_current, [mean_prior, std_prior], \ [mean_prior, std_prior], data) if np.random.rand() < acceptance_prob: mean_current = mean_proposal std_current = std_proposal trace['mean'].append(mean_current) trace['std'].append(std_current) return traceMarge d'amélioration
Log est votre ami !
Rappelons a * b = antilog(log(a) + log(b)) et a / b = antilog(log(a) - log(b)).
Cela nous est bénéfique car nous aurons affaire à de très petites probabilités, multipliant ce qui donnera zéro, nous ajouterons donc plutôt le log prob, problème résolu !
Ainsi, notre code précédent devient :
def accept_proposal(mean_proposal, std_proposal, mean_current, \ std_current, prior_mean, prior_std, data): def prior(mean, std, prior_mean, prior_std): return st.norm(prior_mean[0], prior_mean[1]).logpdf(mean)+ \ st.norm(prior_std[0], prior_std[1]).logpdf(std) def likelihood(mean, std, data): return np.sum(st.norm(mean, std).logpdf(X)) prior_current = prior(mean_current, std_current, prior_mean, prior_std) likelihood_current = likelihood(mean_current, std_current, data) prior_proposal = prior(mean_proposal, std_proposal, prior_mean, prior_std) likelihood_proposal = likelihood(mean_proposal, std_proposal, data) return (prior_proposal + likelihood_proposal) - (prior_current + likelihood_current)Puisque nous renvoyons le log de probabilité d'acceptation :
if np.random.rand() < acceptance_prob:
Devient:
if math.log(np.random.rand()) < acceptance_prob:
Exécutons le nouveau code et traçons les résultats.
_ = plt.hist(trace['std'], bins = 50, label = "std") _ = plt.hist(trace['mean'], bins = 50, label = "mean") _ = plt.legend()Comme vous pouvez le voir, la norme est centrée sur 1,2 et la moyenne sur 1,5. Nous l'avons fait!
Avancer
À présent, vous comprenez, espérons-le, comment fonctionne Metropolis-Hastings et vous vous demandez peut-être où vous pouvez l'utiliser.
Eh bien, Bayesian Methods for Hackers est un excellent livre qui explique la programmation probabiliste, et si vous voulez en savoir plus sur le théorème de Bayes et ses applications, Think Bayes est un excellent livre d'Allen B. Downey.
Merci d'avoir lu, et j'espère que cet article vous encouragera à découvrir le monde incroyable des statistiques bayésiennes.
