MCMC 方法:Metropolis-Hastings 和贝叶斯推理
已发表: 2022-03-11让我们弄清楚基本定义:马尔可夫链蒙特卡罗 (MCMC) 方法让我们可以从分布中计算样本,即使我们无法计算它。
这是什么意思? 让我们回过头来谈谈蒙特卡洛抽样。
蒙特卡洛抽样
什么是蒙特卡罗方法?
“蒙特卡洛方法或蒙特卡洛实验是一类广泛的计算算法,它依赖于重复随机抽样来获得数值结果。” (维基百科)
让我们分解一下。
示例 1:面积估计
想象一下你有一个不规则的形状,如下图所示:
你的任务是确定这个形状所包围的区域。 您可以使用的一种方法是在形状中制作小正方形,计算正方形,这将为您提供一个非常准确的面积近似值。 然而,这既困难又耗时。
蒙特卡洛采样来救援!
首先,我们在形状周围画一个已知面积的大正方形,例如 50 平方厘米。 现在我们“悬挂”这个正方形并开始随机向该形状投掷飞镖。
接下来,我们计算矩形中的省道总数和我们感兴趣的形状中的省道数。假设使用的“省道”总数为 100,其中 22 个最终在形状内。 现在可以通过简单的公式计算面积:
形状面积=正方形面积*(形状中的飞镖数)/(正方形中的飞镖数)
所以,在我们的例子中,这归结为:
形状面积 = 50 * 22/100 = 11 cm2
如果我们将“飞镖”的数量乘以 10 倍,这个近似值将非常接近真实答案:
形状面积 = 50 * 280/1000 = 14 cm2
这就是我们如何通过使用蒙特卡罗抽样来分解复杂的任务,就像上面给出的那样。
大数定律
我们投的飞镖越多,面积近似值越接近,这是因为大数定律:
“大数定律是描述多次执行相同实验的结果的定理。 按照法律规定,大量试验得到的结果的平均值应该接近预期值,并且随着试验次数的增加而趋于接近。”
这将我们带到下一个例子,著名的蒙蒂霍尔问题。
示例 2:蒙蒂霍尔问题
蒙蒂霍尔问题是一个非常有名的脑筋急转弯:
“一共有三扇门,一扇后面是一辆车,其他的后面是一只山羊。 你选择一扇门,主人打开另一扇门,告诉你门后有一只山羊。 然后他问你是否想改变你的决定。 你? 为什么? 为什么不?”
您首先想到的是,无论您是否切换,获胜的机会都是平等的,但事实并非如此。 让我们制作一个简单的流程图来演示。
假设汽车在 3 号门后面:
因此,如果你切换,你赢了 ⅔ 次,如果你不切换,你只赢了 ⅓ 次。
让我们通过采样来解决这个问题。
wins = [] for i in range(int(10e6)): car_door = assign_car_door() choice = random.randint(0, 2) opened_door = assign_door_to_open(car_door) did_he_win = win_or_lose(choice, car_door, opened_door, switch = False) wins.append(did_he_win) print(sum(wins)/len(wins)) assign_car_door()函数只是一个随机数生成器,用于选择门 0、1 或 2,在门后有汽车。 使用assign_door_to_open选择一扇门,门后面有一只山羊,但不是您选择的门,主机打开它。 win_or_lose返回true或false ,表示您是否赢得了汽车,它需要一个布尔“开关”,表示您是否切换了门。
让我们运行这个模拟 1000 万次:
- 不切换中奖概率:0.334134
- 如果你切换获胜的概率:0.667255
这与流程图给我们的答案非常接近。
事实上,我们运行这个模拟的次数越多,答案就越接近真实值,从而验证了大数定律:
从这张表中也可以看出:
| 模拟运行 | 换手后中奖概率 | 如果您不切换,获胜的概率 |
| 10 | 0.6 | 0.2 |
| 10^2 | 0.63 | 0.33 |
| 10^3 | 0.661 | 0.333 |
| 10^4 | 0.6683 | 0.3236 |
| 10^5 | 0.66762 | 0.33171 |
| 10^6 | 0.667255 | 0.334134 |
| 10^7 | 0.6668756 | 0.3332821 |
贝叶斯思维方式
“频率学家,被称为统计学的更经典版本,假设概率是事件的长期频率(因此被授予标题)。”
“贝叶斯统计是统计领域的一种理论,它基于概率的贝叶斯解释,其中概率表示对事件的相信程度。 信念程度可能基于对事件的先验知识,例如先前实验的结果,或基于对事件的个人信念。” - 来自黑客的概率编程和贝叶斯方法
这是什么意思?
在频率论者的思维方式中,我们从长远角度看待概率。 当一位常客说发生车祸的可能性为 0.001% 时,这意味着,如果我们考虑无限次的汽车旅行,其中 0.001% 的车祸将以车祸告终。
贝叶斯的心态是不同的,因为我们从一个先验开始,一个信念。 如果我们谈论 0 的信念,这意味着您的信念是事件永远不会发生; 相反,信念为 1 意味着您确信它会发生。
然后,一旦我们开始观察数据,我们就会更新这个信念以考虑数据。 我们如何做到这一点? 通过使用贝叶斯定理。
贝叶斯定理
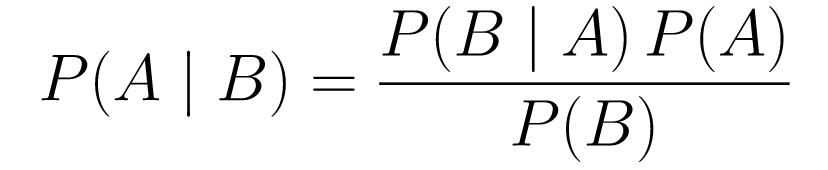 ....(1)
....(1)让我们分解一下。
-
P(A | B)给出了给定事件 B 的事件 A 的概率。这是后验概率,B 是我们观察到的数据,所以考虑到我们观察到的数据,我们本质上是在说事件发生的概率是多少。 -
P(A)是先验的,我们相信事件 A 会发生。 -
P(B | A)是可能性,假设 A 为真,我们观察数据的概率是多少。
让我们看一个例子,癌症筛查测试。
癌症的概率
假设一位患者去做乳房 X 光检查,而乳房 X 光检查结果呈阳性。 患者实际上患有癌症的概率是多少?
让我们定义概率:
- 1% 的女性患有乳腺癌。
- 乳房 X 线照片在 80% 的时间里检测到癌症实际上存在。
- 9.6% 的乳房 X 线照片错误地报告您患有癌症,而实际上您并没有患上癌症。
因此,如果您说如果乳房 X 光检查结果呈阳性,则意味着您有 80% 的机会患有癌症,那将是错误的。 您不会考虑到患癌症是一种罕见的事件,即只有 1% 的女性患有乳腺癌。 我们需要将此作为先决条件,这就是贝叶斯定理发挥作用的地方:
P(C+ | T+) =(P(T+|C+)*P(C+))/P(T+)
-
P(C+ | T+):这是癌症存在的概率,假设测试是阳性的,这就是我们感兴趣的。 -
P(T+ | C+):这是测试为阳性的概率,假设存在癌症,如上所述,这等于 80% = 0.8。 -
P(C+):这是先验概率,一个人患癌症的概率,等于 1% = 0.01。 -
P(T+):这是测试为阳性的概率,无论如何,它有两个分量: P(T+) = P(T+|C-) P(C-)+P(T+|C+) P (C+) -
P(T+ | C-):这是检测结果呈阳性但没有癌症的概率,由 0.096 给出。 -
P(C-):这是没有患癌症的概率,因为患癌症的概率是 1%,这等于 99% = 0.99。 -
P(T+ | C+):这是检测结果呈阳性的概率,假设您患有癌症,这等于 80% = 0.8。 -
P(C+):这是患癌症的概率,等于 1% = 0.01。
将所有这些代入原始公式:
因此,鉴于乳房 X 光检查结果呈阳性,患者患癌症的几率为 7.76%。 起初可能看起来很奇怪,但它是有道理的。 该测试给出了 9.6% 的假阳性(相当高),因此在给定的人群中会有很多假阳性。 对于一种罕见的疾病,大多数阳性检测结果都是错误的。
现在让我们重新审视蒙蒂霍尔问题并使用贝叶斯定理解决它。
蒙蒂霍尔问题
先验可以定义为:
- 假设您一开始选择门 A 作为您的选择。
- P(H) = ⅓, ⅓。 ⅓ 对于所有三个门,这意味着在门打开并且山羊露出之前,汽车在其中任何一个后面的机会均等。
可能性可以定义为:
-
P(D|H),其中事件 D 是蒙蒂选择了门 B 并且后面没有车。 - 如果汽车在门 A 后面,则
P(D|H)= 1/2 - 因为他有 50% 的机会选择 B 门,而他有 50% 的机会选择门 C。 - 如果汽车在门 B 后面,则
P(D|H)= 0,因为如果汽车在门 B 后面,他有 0% 的机会选择门 B。 -
P(D|H)= 1 如果汽车在 C 后面,而你选择 A,那么他有 100% 的概率会选择 B 门。
我们对P(H|D)感兴趣,这是汽车在门后面的概率,因为它向我们展示了一只山羊在其他门后面。
从后验P(H|D)可以看出,从 A 切换到门 C 会增加获胜的概率。
大都会-黑斯廷斯
现在,让我们结合目前为止介绍的所有内容,并尝试了解 Metropolis-Hastings 的工作原理。
Metropolis-Hastings 使用贝叶斯定理获得复杂分布的后验分布,很难从中直接采样。
如何? 本质上,它从一个空间中随机选择不同的样本并检查新样本是否比上一个样本更有可能来自后验,因为我们正在查看等式(1)中的概率比 P(B),得到取消:
P(acceptance) = ( P(newSample) * 新样本的可能性) / (P(oldSample) * 旧样本的可能性)

每个新样本的“可能性”由函数f决定。 这就是为什么f必须与我们要从中采样的后验成正比的原因。
为了决定是接受还是拒绝 θ',必须为每个新提议的 θ' 计算以下比率:
其中 θ 是旧样本, P(D| θ)是样本 θ 的似然性。
让我们用一个例子来更好地理解这一点。 假设您有数据,但您想找出适合它的正态分布,所以:
X ~ N(平均,标准)
现在我们需要定义均值和标准的先验。 为简单起见,我们假设两者都服从均值 1 和标准差 2 的正态分布:
均值 ~ N(1, 2)
标准~N(1, 2)
现在,让我们生成一些数据并假设真实均值和标准差分别为 0.5 和 1.2。
import numpy as np import matplotlib.pyplot as plt import scipy.stats as st meanX = 1.5 stdX = 1.2 X = np.random.normal(meanX, stdX, size = 1000) _ = plt.hist(X, bins = 50)PyMC3
让我们首先使用一个名为PyMC3的库来对数据进行建模并找到均值和标准差的后验分布。
import pymc3 as pm with pm.Model() as model: mean = pm.Normal("mean", mu = 1, sigma = 2) std = pm.Normal("std", mu = 1, sigma = 2) x = pm.Normal("X", mu = mean, sigma = std, observed = X) step = pm.Metropolis() trace = pm.sample(5000, step = step)让我们回顾一下代码。
首先,我们定义均值和标准差的先验,即均值 1 和标准差 2 的法线。
x = pm.Normal(“X”,mu = mean,sigma = std,observed = X)
在这一行中,我们定义了我们感兴趣的变量; 它采用我们之前定义的平均值和标准差,它还采用我们之前计算的观察值。
让我们看看结果:
_ = plt.hist(trace['std'], bins = 50, label = "std") _ = plt.hist(trace['mean'], bins = 50, label = "mean") _ = plt.legend()标准以 1.2 为中心,平均值为 1.55 - 非常接近!
现在让我们从头开始了解 Metropolis-Hastings。
从头开始
生成提案
首先,让我们了解 Metropolis-Hastings 是做什么的。 在本文前面,我们说过, “Metropolis-Hastings 从一个空间中随机选择不同的样本”,但它如何知道要选择哪个样本呢?
它使用提案分布来做到这一点。 它是一个以当前接受的样本为中心的正态分布,STD 为 0.5。 其中 0.5 是超参数,我们可以调整; 提案的 STD 越多,它将从当前接受的样本中搜索得越远。 让我们对此进行编码。
由于我们必须找到分布的均值和标准差,因此该函数将采用当前接受的均值和当前接受的标准差,并返回两者的建议。
def get_proposal(mean_current, std_current, proposal_width = 0.5): return np.random.normal(mean_current, proposal_width), \ np.random.normal(std_current, proposal_width)接受/拒绝提案
现在,让我们编写接受或拒绝提案的逻辑。 它有两部分:先验和可能性。
首先,让我们计算提案来自先验的概率:
def prior(mean, std, prior_mean, prior_std): return st.norm(prior_mean[0], prior_mean[1]).pdf(mean)* \ st.norm(prior_std[0], prior_std[1]).pdf(std)它只取均值和标准差并计算该均值和标准差来自我们定义的先验分布的可能性。
在计算可能性时,我们计算我们看到的数据来自建议分布的可能性。
def likelihood(mean, std, data): return np.prod(st.norm(mean, std).pdf(X))因此,对于每个数据点,我们乘以该数据点来自建议分布的概率。
现在,我们需要为当前的均值和标准以及建议的均值和标准调用这些函数。
prior_current = prior(mean_current, std_current, prior_mean, prior_std) likelihood_current = likelihood(mean_current, std_current, data) prior_proposal = prior(mean_proposal, std_proposal, prior_mean, prior_std) likelihood_proposal = likelihood(mean_proposal, std_proposal, data)整个代码:
def accept_proposal(mean_proposal, std_proposal, mean_current, \ std_current, prior_mean, prior_std, data): def prior(mean, std, prior_mean, prior_std): return st.norm(prior_mean[0], prior_mean[1]).pdf(mean)* \ st.norm(prior_std[0], prior_std[1]).pdf(std) def likelihood(mean, std, data): return np.prod(st.norm(mean, std).pdf(X)) prior_current = prior(mean_current, std_current, prior_mean, prior_std) likelihood_current = likelihood(mean_current, std_current, data) prior_proposal = prior(mean_proposal, std_proposal, prior_mean, prior_std) likelihood_proposal = likelihood(mean_proposal, std_proposal, data) return (prior_proposal * likelihood_proposal) / (prior_current * likelihood_current)现在,让我们创建最终函数,将所有内容联系在一起并生成我们需要的后验样本。
生成后验
现在,我们调用上面编写的函数并生成后验!
def get_trace(data, samples = 5000): mean_prior = 1 std_prior = 2 mean_current = mean_prior std_current = std_prior trace = { "mean": [mean_current], "std": [std_current] } for i in tqdm(range(samples)): mean_proposal, std_proposal = get_proposal(mean_current, std_current) acceptance_prob = accept_proposal(mean_proposal, std_proposal, mean_current, \ std_current, [mean_prior, std_prior], \ [mean_prior, std_prior], data) if np.random.rand() < acceptance_prob: mean_current = mean_proposal std_current = std_proposal trace['mean'].append(mean_current) trace['std'].append(std_current) return trace改进空间
日志是你的朋友!
回想一下a * b = antilog(log(a) + log(b))和a / b = antilog(log(a) - log(b)).
这对我们有利,因为我们将处理非常小的概率,相乘将导致零,所以我们宁愿添加对数概率,问题解决了!
所以,我们之前的代码变成了:
def accept_proposal(mean_proposal, std_proposal, mean_current, \ std_current, prior_mean, prior_std, data): def prior(mean, std, prior_mean, prior_std): return st.norm(prior_mean[0], prior_mean[1]).logpdf(mean)+ \ st.norm(prior_std[0], prior_std[1]).logpdf(std) def likelihood(mean, std, data): return np.sum(st.norm(mean, std).logpdf(X)) prior_current = prior(mean_current, std_current, prior_mean, prior_std) likelihood_current = likelihood(mean_current, std_current, data) prior_proposal = prior(mean_proposal, std_proposal, prior_mean, prior_std) likelihood_proposal = likelihood(mean_proposal, std_proposal, data) return (prior_proposal + likelihood_proposal) - (prior_current + likelihood_current)因为我们要返回接受概率的对数:
if np.random.rand() < acceptance_prob:
变成:
if math.log(np.random.rand()) < acceptance_prob:
让我们运行新代码并绘制结果。
_ = plt.hist(trace['std'], bins = 50, label = "std") _ = plt.hist(trace['mean'], bins = 50, label = "mean") _ = plt.legend()如您所见, std以 1.2 为中心,平均值以 1.5 为中心。 我们做到了!
向前进
到目前为止,您希望了解 Metropolis-Hastings 的工作原理,并且您可能想知道在哪里可以使用它。
好吧, Bayesian Methods for Hackers是一本解释概率编程的优秀书籍,如果你想了解更多关于贝叶斯定理及其应用的信息, Think Bayes是 Allen B. Downey 的一本好书。
感谢您的阅读,我希望这篇文章能鼓励您探索贝叶斯统计的奇妙世界。
