วิธีการ MCMC: มหานคร-เฮสติ้งส์และการอนุมานแบบเบย์
เผยแพร่แล้ว: 2022-03-11มาดูคำจำกัดความพื้นฐานกัน: วิธีการของ Markov Chain Monte Carlo (MCMC) ให้เราคำนวณตัวอย่างจากการแจกแจงแม้ว่าเราจะคำนวณไม่ได้ก็ตาม
สิ่งนี้หมายความว่า? กลับมาคุยกันเรื่องการสุ่มตัวอย่างมอนติคาร์โลกัน
การสุ่มตัวอย่างมอนติคาร์โล
วิธีมอนติคาร์โลคืออะไร?
"วิธีมอนติคาร์โลหรือการทดลองของมอนติคาร์โลเป็นอัลกอริธึมการคำนวณแบบกว้าง ๆ ซึ่งอาศัยการสุ่มตัวอย่างซ้ำ ๆ เพื่อให้ได้ผลลัพธ์ที่เป็นตัวเลข" (วิกิพีเดีย)
มาทำลายมันกันเถอะ
ตัวอย่างที่ 1: การประมาณพื้นที่
ลองนึกภาพว่าคุณมีรูปร่างผิดปกติเช่นรูปร่างที่แสดงด้านล่าง:
และคุณได้รับมอบหมายให้กำหนดพื้นที่ที่ล้อมรอบด้วยรูปร่างนี้ วิธีหนึ่งที่คุณสามารถใช้ได้คือสร้างสี่เหลี่ยมเล็กๆ ในรูป นับกำลังสอง และนั่นจะทำให้คุณประมาณพื้นที่ได้อย่างแม่นยำ อย่างไรก็ตาม นั่นเป็นเรื่องยากและใช้เวลานาน
มอนติคาร์โลสุ่มตัวอย่างเพื่อช่วยชีวิต!
ขั้นแรก เราวาดสี่เหลี่ยมขนาดใหญ่ของพื้นที่ที่ทราบรอบๆ รูปร่าง เช่น 50 cm2 ตอนนี้เรา "แขวน" จัตุรัสนี้แล้วเริ่มขว้างปาเป้าไปที่รูปร่างแบบสุ่ม
ต่อไป เราจะนับจำนวนลูกดอกทั้งหมดในสี่เหลี่ยมผืนผ้าและจำนวนลูกดอกในรูปทรงที่เราสนใจ สมมติว่าจำนวน "ลูกดอก" ที่ใช้ทั้งหมดคือ 100 และ 22 ลูกดอกนั้นอยู่ในรูปทรงนั้น ตอนนี้พื้นที่สามารถคำนวณได้โดยสูตรง่ายๆ:
พื้นที่ของรูปทรง = พื้นที่ของสี่เหลี่ยมจัตุรัส *(จำนวนลูกดอกในรูปทรง) / (จำนวนลูกดอกในสี่เหลี่ยมจัตุรัส)
ดังนั้น ในกรณีของเรา สิ่งนี้ลงมาเพื่อ:
พื้นที่รูปร่าง = 50 * 22/100 = 11 cm2
หากเราคูณจำนวน "ลูกดอก" ด้วยปัจจัย 10 การประมาณนี้จะใกล้เคียงกับคำตอบจริงมาก:
พื้นที่รูปร่าง = 50 * 280/1000 = 14 cm2
นี่คือวิธีที่เราแยกย่อยงานที่ซับซ้อน เช่น งานที่ระบุข้างต้น โดยใช้การสุ่มตัวอย่างมอนติคาร์โล
กฎของตัวเลขขนาดใหญ่
ยิ่งเราขว้างปาลูกดอกใกล้พื้นที่มากขึ้น และนี่เป็นเพราะกฎของตัวเลขมาก:
“กฎจำนวนมากเป็นทฤษฎีบทที่อธิบายผลลัพธ์ของการทดลองเดียวกันหลายครั้ง ตามกฎหมาย ค่าเฉลี่ยของผลลัพธ์ที่ได้จากการทดลองจำนวนมากควรใกล้เคียงกับค่าที่คาดหวัง และมีแนวโน้มที่จะเข้าใกล้มากขึ้นเมื่อมีการทดลองมากขึ้น”
สิ่งนี้นำเราไปสู่ตัวอย่างต่อไป ปัญหา Monty Hall ที่มีชื่อเสียง
ตัวอย่างที่ 2: ปัญหามอนตี้ฮอลล์
ปัญหา Monty Hall เป็นเกมพัฒนาสมองที่มีชื่อเสียงมาก:
“มีประตูสามบาน บานหนึ่งมีรถอยู่ข้างหลัง อีกบานมีแพะอยู่ข้างหลัง คุณเลือกประตู เจ้าบ้านเปิดประตูอีกบานหนึ่ง และแสดงให้คุณเห็นว่ามีแพะอยู่ข้างหลัง จากนั้นเขาจะถามคุณว่าคุณต้องการเปลี่ยนการตัดสินใจหรือไม่ คุณล่ะ? ทำไม? ทำไมจะไม่ล่ะ?"
สิ่งแรกที่คุณนึกถึงคือโอกาสในการชนะจะเท่ากันไม่ว่าคุณจะเปลี่ยนหรือไม่เปลี่ยน แต่นั่นไม่เป็นความจริง มาสร้างผังงานอย่างง่ายเพื่อสาธิตสิ่งเดียวกัน
สมมติว่ารถอยู่หลังประตู 3:
ดังนั้น หากคุณเปลี่ยน คุณจะชนะ ⅔ ครั้ง และถ้าคุณไม่เปลี่ยน คุณจะชนะเพียง ⅓ ครั้งเท่านั้น
ลองแก้ปัญหานี้โดยใช้การสุ่มตัวอย่าง
wins = [] for i in range(int(10e6)): car_door = assign_car_door() choice = random.randint(0, 2) opened_door = assign_door_to_open(car_door) did_he_win = win_or_lose(choice, car_door, opened_door, switch = False) wins.append(did_he_win) print(sum(wins)/len(wins)) assign_car_door() เป็นเพียงตัวสร้างตัวเลขสุ่มที่เลือกประตู 0, 1 หรือ 2 ซึ่งมีรถยนต์อยู่ด้านหลัง การใช้ assign_door_to_open จะเป็นการเลือกประตูที่มีแพะอยู่ข้างหลัง และไม่ใช่ประตูที่คุณเลือก และโฮสต์ก็เปิดประตูนั้น win_or_lose คืนค่า true หรือ false ซึ่งหมายความว่าคุณชนะรถหรือไม่ มันใช้ "สวิตช์" แบบบูลที่บอกว่าคุณเปลี่ยนประตูหรือไม่
เรียกใช้การจำลองนี้ 10 ล้านครั้ง:
- ความน่าจะเป็นที่จะชนะถ้าคุณไม่เปลี่ยน: 0.334134
- ความน่าจะเป็นที่จะชนะหากคุณเปลี่ยน: 0.667255
ซึ่งใกล้เคียงกับคำตอบที่ผังงานให้ไว้มาก
อันที่จริง ยิ่งเราใช้การจำลองนี้มากเท่าไร คำตอบก็ยิ่งเข้าใกล้มูลค่าที่แท้จริงมากขึ้นเท่านั้น จึงเป็นการตรวจสอบกฎของตัวเลขจำนวนมาก:
เช่นเดียวกันสามารถเห็นได้จากตารางนี้:
| การจำลองการทำงาน | ความน่าจะเป็นในการชนะหากคุณเปลี่ยน | ความน่าจะเป็นในการชนะถ้าคุณไม่เปลี่ยน |
| 10 | 0.6 | 0.2 |
| 10^2 | 0.63 | 0.33 |
| 10^3 | 0.661 | 0.333 |
| 10^4 | 0.6683 | 0.3236 |
| 10^5 | 0.66762 | 0.33171 |
| 10^6 | 0.667255 | 0.334134 |
| 10^7 | 0.6668756 | 0.3332821 |
วิถีแห่งการคิดแบบเบส์
"Frequentist หรือที่เรียกว่าสถิติเวอร์ชันคลาสสิกมากกว่า ถือว่าความน่าจะเป็นคือความถี่ของเหตุการณ์ในระยะยาว (ด้วยเหตุนี้จึงเป็นชื่อที่มอบให้)"
“สถิติแบบเบย์เป็นทฤษฎีในด้านสถิติโดยอิงจากการตีความความน่าจะเป็นแบบเบย์ โดยที่ความน่าจะเป็นแสดงถึงระดับของความเชื่อในเหตุการณ์หนึ่ง ระดับความเชื่ออาจขึ้นอยู่กับความรู้เดิมเกี่ยวกับเหตุการณ์ เช่น ผลการทดลองครั้งก่อน หรือความเชื่อส่วนบุคคลเกี่ยวกับเหตุการณ์” - จาก Probabilistic Programming และ Bayesian Methods for Hackers
สิ่งนี้หมายความว่า?
ในวิธีคิดที่ใช้บ่อย เราจะพิจารณาความน่าจะเป็นในระยะยาว เมื่อคนใช้บ่อยบอกว่ามีโอกาส 0.001% ที่จะเกิดอุบัติเหตุรถชน หมายความว่า หากเราพิจารณาการเดินทางด้วยรถยนต์ที่ไม่มีที่สิ้นสุด 0.001% ของการเดินทางทั้งหมดจะจบลงด้วยอุบัติเหตุ
ความคิดแบบเบย์นั้นแตกต่างไปจากเดิมเมื่อเราเริ่มต้นด้วยความเชื่อก่อนหน้านี้ ถ้าเราพูดถึงความเชื่อที่เป็น 0 แสดงว่าความเชื่อของคุณคือเหตุการณ์จะไม่เกิดขึ้น ในทางกลับกัน ความเชื่อ 1 หมายความว่าคุณแน่ใจว่ามันจะเกิดขึ้น
จากนั้นเมื่อเราเริ่มสังเกตข้อมูล เราจะอัปเดตความเชื่อนี้เพื่อพิจารณาข้อมูล เราจะทำเช่นนี้ได้อย่างไร? โดยใช้ทฤษฎีบทเบย์
ทฤษฎีบทเบย์
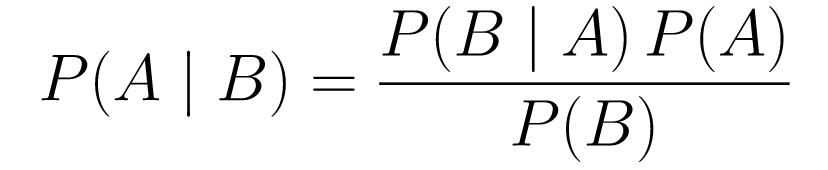 ....(1)
....(1)มาทำลายมันกันเถอะ
-
P(A | B)ให้ค่าความน่าจะเป็นของเหตุการณ์ A กับเหตุการณ์ B นี่คือส่วนหลัง B คือข้อมูลที่เราสังเกต ดังนั้นเรากำลังพูดถึงความน่าจะเป็นของเหตุการณ์ที่เกิดขึ้น โดยพิจารณาจากข้อมูลที่เราสังเกต -
P(A)เป็นเหตุการณ์ก่อนหน้า เราเชื่อว่าเหตุการณ์ A จะเกิดขึ้น -
P(B | A)คือความน่าจะเป็น ความน่าจะเป็นที่เราจะสังเกตข้อมูลที่ A เป็นจริงเป็นเท่าใด
มาดูตัวอย่าง การตรวจคัดกรองมะเร็ง
ความน่าจะเป็นของมะเร็ง
สมมติว่าผู้ป่วยไปตรวจแมมโมแกรม และการตรวจแมมโมแกรมกลับเป็นบวก ความน่าจะเป็นที่ผู้ป่วยเป็นมะเร็งจริง ๆ เป็นเท่าไหร่?
มากำหนดความน่าจะเป็นกัน:
- ผู้หญิง 1% เป็นมะเร็งเต้านม
- แมมโมแกรมตรวจพบมะเร็ง 80% ของเวลาที่เป็นอยู่จริง
- 9.6% ของแมมโมแกรมรายงานเท็จว่าคุณเป็นมะเร็งโดยที่คุณไม่มีจริงๆ
ดังนั้น ถ้าคุณจะพูดว่าถ้าแมมโมแกรมกลับมาเป็นบวก หมายความว่ามีโอกาส 80% ที่คุณจะเป็นมะเร็ง นั่นถือว่าผิด คุณจะไม่คำนึงถึงว่าการเป็นมะเร็งเป็นเหตุการณ์ที่เกิดขึ้นได้ยาก กล่าวคือ มีผู้หญิงเพียง 1% เท่านั้นที่เป็นมะเร็งเต้านม เราต้องใช้สิ่งนี้ก่อนหน้านี้ และนี่คือจุดเริ่มต้นของทฤษฎีบทเบย์:
P(C+ | T+) =(P(T+|C+)*P(C+))/P(T+)
-
P(C+ | T+): นี่คือความน่าจะเป็นที่จะมีมะเร็ง เมื่อผลการทดสอบเป็นบวก นี่คือสิ่งที่เราสนใจ -
P(T+ | C+): นี่คือความน่าจะเป็นที่การทดสอบเป็นบวก เนื่องจากเป็นมะเร็ง ตามที่กล่าวข้างต้นจะเท่ากับ 80% = 0.8 -
P(C+): นี่คือความน่าจะเป็นก่อนหน้า ความน่าจะเป็นของบุคคลที่เป็นมะเร็ง ซึ่งเท่ากับ 1% = 0.01 -
P(T+): นี่คือความน่าจะเป็นที่การทดสอบเป็นบวก ไม่ว่าจะเกิดอะไรขึ้น ดังนั้นมันจึงมีองค์ประกอบสองส่วน: P(T+) = P(T+|C-) P(C-)+P(T+|C+) P (ซี+) -
P(T+ | C-): นี่คือความน่าจะเป็นที่การทดสอบกลับมาเป็นบวก แต่ไม่มีมะเร็ง มีค่าเท่ากับ 0.096 -
P(C-): นี่คือความน่าจะเป็นที่จะไม่เป็นมะเร็งเนื่องจากความน่าจะเป็นที่จะเป็นมะเร็งคือ 1% ซึ่งเท่ากับ 99% = 0.99 -
P(T+ | C+): นี่คือความน่าจะเป็นที่การทดสอบกลับมาเป็นบวก เนื่องจากคุณเป็นมะเร็ง นี่จะเท่ากับ 80% = 0.8 -
P(C+): นี่คือความน่าจะเป็นที่จะเป็นมะเร็ง ซึ่งเท่ากับ 1% = 0.01
เสียบทั้งหมดนี้ลงในสูตรดั้งเดิม:
ดังนั้น จากการตรวจแมมโมแกรมกลับเป็นบวก มีโอกาส 7.76% ที่ผู้ป่วยจะเป็นมะเร็ง มันอาจจะดูแปลกในตอนแรกแต่ก็สมเหตุสมผล การทดสอบให้ผลบวกลวง 9.6% ของเวลา (ค่อนข้างสูง) ดังนั้นจะมีผลบวกลวงจำนวนมากในประชากรที่กำหนด สำหรับโรคที่หายาก ผลการทดสอบในเชิงบวกส่วนใหญ่จะผิดพลาด
ตอนนี้ให้เราทบทวนปัญหา Monty Hall และแก้ไขโดยใช้ทฤษฎีบท Bayes
ปัญหามอนตี้ฮอลล์
นักบวชสามารถกำหนดได้ดังนี้:
- สมมติว่าคุณเลือกประตู A เป็นตัวเลือกของคุณในตอนเริ่มต้น
- P(H) = ⅓, ⅓. ⅓ สำหรับทั้งสามประตู ซึ่งหมายความว่าก่อนที่ประตูจะเปิดและแพะเปิดเผย มีโอกาสเท่ากันที่รถจะแซงหลังประตูใดประตูหนึ่ง
ความน่าจะเป็นสามารถกำหนดได้ดังนี้:
-
P(D|H)โดยที่เหตุการณ์ D คือมอนตี้เลือกประตู B และไม่มีรถอยู่ข้างหลัง -
P(D|H)= 1/2 ถ้ารถอยู่หลังประตู A - เนื่องจากมีโอกาส 50% ที่เขาจะเลือกประตู B และโอกาส 50% ที่จะเลือกประตู C -
P(D|H)= 0 ถ้ารถอยู่หลังประตู B เนื่องจากมีโอกาส 0% ที่เขาจะเลือกประตู B ถ้ารถอยู่ข้างหลัง -
P(D|H)= 1 ถ้ารถอยู่หลัง C และคุณเลือก A มีความเป็นไปได้ 100% ที่เขาจะเลือกประตู B
เราสนใจ P(H|D) ซึ่งเป็นความน่าจะเป็นที่รถอยู่หลังประตู เพราะมันทำให้เราเห็นแพะอยู่หลังประตูอีกบานหนึ่ง

จากด้านหลังจะเห็นได้ว่า P(H|D) การเปลี่ยนไปใช้ประตู C จาก A จะเพิ่มโอกาสในการชนะ
เมโทรโพลิส-เฮสติงส์
ตอนนี้ มารวมทุกสิ่งที่เราพูดถึงไปแล้วและพยายามทำความเข้าใจว่า Metropolis-Hastings ทำงานอย่างไร
เมโทรโพลิส-เฮสติงส์ใช้ทฤษฎีบทเบย์เพื่อให้ได้การกระจายตัวหลังของการแจกแจงเชิงซ้อน ซึ่งการสุ่มตัวอย่างโดยตรงเป็นเรื่องยาก
ยังไง? โดยพื้นฐานแล้ว มันจะสุ่มเลือกตัวอย่างต่างๆ จากช่องว่างและตรวจสอบว่าตัวอย่างใหม่มีแนวโน้มว่าจะมาจากหลังมากกว่าตัวอย่างสุดท้ายหรือไม่ เนื่องจากเรากำลังดูอัตราส่วนของความน่าจะเป็น P(B) ในสมการ (1) จะได้ ยกเลิก:
P(acceptance) = ( P(newSample) * ความน่าจะเป็นของตัวอย่างใหม่) / (P(oldSample) * ความน่าจะเป็นของตัวอย่างเก่า)
"ความน่าจะเป็น" ของตัวอย่างใหม่แต่ละตัวอย่างถูกกำหนดโดยฟังก์ชัน ฉ . นั่นเป็นสาเหตุที่ f ต้องเป็นสัดส่วนกับส่วนหลังที่เราต้องการสุ่มตัวอย่าง
ในการตัดสินใจว่า θ′ จะได้รับการยอมรับหรือปฏิเสธหรือไม่ จะต้องคำนวณอัตราส่วนต่อไปนี้สำหรับ θ ที่เสนอใหม่แต่ละรายการ:
โดยที่ θ คือตัวอย่างเก่า P(D| θ) คือความน่าจะเป็นของตัวอย่าง θ
ลองใช้ตัวอย่างเพื่อทำความเข้าใจสิ่งนี้ให้ดีขึ้น สมมติว่าคุณมีข้อมูลแต่คุณต้องการหาการกระจายตัวแบบปกติที่พอดี ดังนั้น:
X ~ N(ค่าเฉลี่ย มาตรฐาน)
ตอนนี้ เราต้องกำหนดไพร่พลสำหรับค่าเฉลี่ยและมาตรฐานทั้งคู่ เพื่อความง่าย เราจะถือว่าทั้งคู่ทำตามการแจกแจงแบบปกติด้วยค่าเฉลี่ย 1 และ std 2:
ค่าเฉลี่ย ~ N(1, 2)
มาตรฐาน ~ N (1, 2)
ตอนนี้ มาสร้างข้อมูลกันและถือว่าค่าเฉลี่ยจริงและ std คือ 0.5 และ 1.2 ตามลำดับ
import numpy as np import matplotlib.pyplot as plt import scipy.stats as st meanX = 1.5 stdX = 1.2 X = np.random.normal(meanX, stdX, size = 1000) _ = plt.hist(X, bins = 50)PyMC3
อันดับแรก ให้ใช้ไลบรารีชื่อ PyMC3 เพื่อสร้างแบบจำลองข้อมูลและค้นหาการแจกแจงภายหลังสำหรับค่าเฉลี่ยและมาตรฐาน
import pymc3 as pm with pm.Model() as model: mean = pm.Normal("mean", mu = 1, sigma = 2) std = pm.Normal("std", mu = 1, sigma = 2) x = pm.Normal("X", mu = mean, sigma = std, observed = X) step = pm.Metropolis() trace = pm.sample(5000, step = step)มาดูโค้ดกัน
อันดับแรก เรากำหนดก่อนหน้าสำหรับค่าเฉลี่ยและ std นั่นคือค่าปกติที่มีค่าเฉลี่ย 1 และ std 2
x = pm.Normal("X", mu = ค่าเฉลี่ย, sigma = std, สังเกต = X)
ในบรรทัดนี้ เรากำหนดตัวแปรที่เราสนใจ มันใช้ค่าเฉลี่ยและมาตรฐานที่เรากำหนดไว้ก่อนหน้านี้ นอกจากนี้ยังใช้ค่าที่สังเกตได้ที่เราคำนวณไว้ก่อนหน้านี้ด้วย
ลองดูผลลัพธ์:
_ = plt.hist(trace['std'], bins = 50, label = "std") _ = plt.hist(trace['mean'], bins = 50, label = "mean") _ = plt.legend()มาตรฐานมีศูนย์กลางอยู่ที่ 1.2 และค่าเฉลี่ยอยู่ที่ 1.55 - ใกล้เคียงกันมาก!
มาทำตั้งแต่เริ่มต้นเพื่อทำความเข้าใจกับ Metropolis-Hastings
ตั้งแต่เริ่มต้น
การสร้างข้อเสนอ
อันดับแรก มาทำความเข้าใจกันว่า Metropolis-Hastings ทำอะไร ก่อนหน้านี้ในบทความนี้ เรากล่าวว่า "เมืองเมโทรโพลิส-เฮสติ้งส์สุ่มเลือกตัวอย่างต่างๆ จากอวกาศ" แต่จะรู้ได้อย่างไรว่าควรเลือกตัวอย่างใด
ทำได้โดยใช้การกระจายข้อเสนอ เป็นการกระจายแบบปกติที่มีศูนย์กลางอยู่ที่ตัวอย่างที่ยอมรับในปัจจุบันและมี STD 0.5 โดยที่ 0.5 เป็นไฮเปอร์พารามิเตอร์ เราสามารถปรับแต่งได้ ยิ่งมี STD ของข้อเสนอมากเท่าใด ข้อเสนอก็จะยิ่งค้นหาจากตัวอย่างที่ยอมรับในปัจจุบันมากขึ้นเท่านั้น มาเขียนโค้ดกัน
เนื่องจากเราต้องหาค่าเฉลี่ยและมาตรฐานของการแจกแจง ฟังก์ชันนี้จะนำค่าเฉลี่ยที่ยอมรับในปัจจุบันและมาตรฐานที่ยอมรับในปัจจุบัน และส่งกลับข้อเสนอสำหรับทั้งคู่
def get_proposal(mean_current, std_current, proposal_width = 0.5): return np.random.normal(mean_current, proposal_width), \ np.random.normal(std_current, proposal_width)การยอมรับ/ปฏิเสธข้อเสนอ
ตอนนี้ มาเขียนโค้ดตรรกะที่ยอมรับหรือปฏิเสธข้อเสนอกัน มันมีสองส่วน: ก่อนหน้า และ โอกาส .
ขั้นแรก ให้คำนวณความน่าจะเป็นของข้อเสนอที่มาจากก่อนหน้านี้:
def prior(mean, std, prior_mean, prior_std): return st.norm(prior_mean[0], prior_mean[1]).pdf(mean)* \ st.norm(prior_std[0], prior_std[1]).pdf(std)มันใช้ ค่าเฉลี่ย และ std แล้วคำนวณว่า ค่าเฉลี่ย และ std นี้มีโอกาสมาจากการ แจกแจงก่อนหน้าที่ เรากำหนดไว้มากน้อยเพียงใด
ในการคำนวณความน่าจะเป็น เราคำนวณความน่าจะเป็นที่ข้อมูลที่เราเห็นมาจากการกระจายที่เสนอ
def likelihood(mean, std, data): return np.prod(st.norm(mean, std).pdf(X))ดังนั้น สำหรับแต่ละจุดข้อมูล เราคูณความน่าจะเป็นของจุดข้อมูลนั้น จากการแจกแจงที่เสนอ
ตอนนี้ เราต้องเรียกฟังก์ชันเหล่านี้สำหรับค่าเฉลี่ยและ std ปัจจุบัน และสำหรับ ค่าเฉลี่ย และ std ที่เสนอ
prior_current = prior(mean_current, std_current, prior_mean, prior_std) likelihood_current = likelihood(mean_current, std_current, data) prior_proposal = prior(mean_proposal, std_proposal, prior_mean, prior_std) likelihood_proposal = likelihood(mean_proposal, std_proposal, data)รหัสทั้งหมด:
def accept_proposal(mean_proposal, std_proposal, mean_current, \ std_current, prior_mean, prior_std, data): def prior(mean, std, prior_mean, prior_std): return st.norm(prior_mean[0], prior_mean[1]).pdf(mean)* \ st.norm(prior_std[0], prior_std[1]).pdf(std) def likelihood(mean, std, data): return np.prod(st.norm(mean, std).pdf(X)) prior_current = prior(mean_current, std_current, prior_mean, prior_std) likelihood_current = likelihood(mean_current, std_current, data) prior_proposal = prior(mean_proposal, std_proposal, prior_mean, prior_std) likelihood_proposal = likelihood(mean_proposal, std_proposal, data) return (prior_proposal * likelihood_proposal) / (prior_current * likelihood_current)ตอนนี้ มาสร้างฟังก์ชันสุดท้ายที่จะผูกทุกอย่างเข้าด้วยกันและสร้างตัวอย่างส่วนหลังที่เราต้องการ
การสร้างส่วนหลัง
ตอนนี้เราเรียกฟังก์ชันที่เราเขียนไว้ด้านบนและสร้างส่วนหลัง!
def get_trace(data, samples = 5000): mean_prior = 1 std_prior = 2 mean_current = mean_prior std_current = std_prior trace = { "mean": [mean_current], "std": [std_current] } for i in tqdm(range(samples)): mean_proposal, std_proposal = get_proposal(mean_current, std_current) acceptance_prob = accept_proposal(mean_proposal, std_proposal, mean_current, \ std_current, [mean_prior, std_prior], \ [mean_prior, std_prior], data) if np.random.rand() < acceptance_prob: mean_current = mean_proposal std_current = std_proposal trace['mean'].append(mean_current) trace['std'].append(std_current) return traceห้องสำหรับการปรับปรุง
บันทึกคือเพื่อนของคุณ!
เรียกคืน a * b = antilog(log(a) + log(b)) และ a / b = antilog(log(a) - log(b)).
สิ่งนี้เป็นประโยชน์สำหรับเราเพราะเราจะจัดการกับความน่าจะเป็นที่น้อยมาก การคูณซึ่งจะส่งผลให้เป็นศูนย์ ดังนั้นเราจะเพิ่มปัญหาของบันทึก แก้ไขปัญหาได้แล้ว!
ดังนั้นรหัสก่อนหน้าของเราจึงกลายเป็น:
def accept_proposal(mean_proposal, std_proposal, mean_current, \ std_current, prior_mean, prior_std, data): def prior(mean, std, prior_mean, prior_std): return st.norm(prior_mean[0], prior_mean[1]).logpdf(mean)+ \ st.norm(prior_std[0], prior_std[1]).logpdf(std) def likelihood(mean, std, data): return np.sum(st.norm(mean, std).logpdf(X)) prior_current = prior(mean_current, std_current, prior_mean, prior_std) likelihood_current = likelihood(mean_current, std_current, data) prior_proposal = prior(mean_proposal, std_proposal, prior_mean, prior_std) likelihood_proposal = likelihood(mean_proposal, std_proposal, data) return (prior_proposal + likelihood_proposal) - (prior_current + likelihood_current)เนื่องจากเราส่งคืนบันทึกความน่าจะเป็นของการยอมรับ:
if np.random.rand() < acceptance_prob:
กลายเป็น:
if math.log(np.random.rand()) < acceptance_prob:
มารันโค้ดใหม่และพล็อตผลลัพธ์กัน
_ = plt.hist(trace['std'], bins = 50, label = "std") _ = plt.hist(trace['mean'], bins = 50, label = "mean") _ = plt.legend()อย่างที่คุณเห็น มาตรฐาน มีศูนย์กลางที่ 1.2 และ ค่าเฉลี่ย ที่ 1.5 เราทำได้!
ก้าวไปข้างหน้า
ถึงตอนนี้ คุณหวังว่าจะเข้าใจวิธีการทำงานของเมโทรโพลิส-เฮสติ้งส์ และคุณอาจสงสัยว่าจะใช้งานที่ไหนได้บ้าง
Bayesian Methods for Hackers เป็นหนังสือที่ยอดเยี่ยมที่อธิบายการเขียนโปรแกรมความน่าจะเป็น และหากคุณต้องการเรียนรู้เพิ่มเติมเกี่ยวกับทฤษฎีบท Bayes และการประยุกต์ใช้ Think Bayes เป็นหนังสือที่ยอดเยี่ยมของ Allen B. Downey
ขอบคุณสำหรับการอ่าน และฉันหวังว่าบทความนี้จะสนับสนุนให้คุณค้นพบโลกอันน่าทึ่งของสถิติแบบเบย์
