Методы MCMC: Метрополис-Гастингс и байесовский вывод
Опубликовано: 2022-03-11Давайте отвлечемся от основного определения: методы Монте-Карло с цепями Маркова (MCMC) позволяют нам вычислять выборки из распределения, даже если мы не можем их вычислить.
Что это значит? Вернемся назад и поговорим о сэмплировании по методу Монте-Карло.
Выборка Монте-Карло
Что такое методы Монте-Карло?
«Методы Монте-Карло или эксперименты Монте-Карло представляют собой широкий класс вычислительных алгоритмов, которые полагаются на повторную случайную выборку для получения числовых результатов». (Википедия)
Давайте сломаем это.
Пример 1: Оценка площади
Представьте, что у вас есть неправильная форма, как форма, представленная ниже:
И перед вами стоит задача определить площадь, ограниченную этой фигурой. Один из методов, который вы можете использовать, состоит в том, чтобы сделать маленькие квадраты в форме, подсчитать квадраты, и это даст вам довольно точное приближение площади. Однако это сложно и требует времени.
Выборка Монте-Карло спешит на помощь!
Сначала рисуем вокруг фигуры большой квадрат известной площади, например, 50 см2. Теперь «подвешиваем» этот квадрат и начинаем хаотично бросать дротики в фигуру.
Далее мы подсчитываем общее количество дротиков в прямоугольнике и количество дротиков в интересующей нас форме. Предположим, что общее количество использованных «дротиков» равно 100 и что 22 из них оказались внутри фигуры. Теперь площадь можно вычислить по простой формуле:
площадь фигуры = площадь квадрата * (количество вытачек в фигуре) / (количество вытачек в квадрате)
Итак, в нашем случае это сводится к:
площадь формы = 50 * 22/100 = 11 см2
Если мы умножим количество «дротиков» на коэффициент 10, это приближение станет очень близким к реальному ответу:
площадь формы = 50 * 280/1000 = 14 см2
Вот как мы разбиваем сложные задачи, подобные приведенной выше, с помощью выборки Монте-Карло.
Закон больших чисел
Аппроксимация площади была тем ближе, чем больше мы бросали дротиков, и это из-за закона больших чисел:
«Закон больших чисел — это теорема, описывающая результат выполнения одного и того же эксперимента большое количество раз. Согласно закону, среднее значение результатов, полученных в результате большого количества испытаний, должно быть близко к ожидаемому значению и будет становиться ближе по мере проведения большего количества испытаний».
Это подводит нас к следующему примеру — знаменитой проблеме Монти Холла.
Пример 2: Задача Монти Холла
Задача Монти Холла — очень известная головоломка:
«Три двери, за одной машина, за другими коза. Вы выбираете дверь, ведущий открывает другую дверь и показывает вам, что за ней стоит коза. Затем он спрашивает вас, хотите ли вы изменить свое решение. Ты? Почему? Почему бы нет?"
Первое, что приходит вам в голову, это то, что шансы на победу равны независимо от того, переключаетесь вы или нет, но это не так. Давайте составим простую блок-схему, чтобы продемонстрировать то же самое.
Предположим, что машина находится за дверью 3:
Следовательно, если вы переключитесь, вы выиграете ⅔ раза, а если не переключитесь, вы выиграете только ⅓ раза.
Давайте решим это с помощью выборки.
wins = [] for i in range(int(10e6)): car_door = assign_car_door() choice = random.randint(0, 2) opened_door = assign_door_to_open(car_door) did_he_win = win_or_lose(choice, car_door, opened_door, switch = False) wins.append(did_he_win) print(sum(wins)/len(wins)) Функция assign_car_door() — это просто генератор случайных чисел, который выбирает дверь 0, 1 или 2, за которой находится машина. Использование assign_door_to_open выбирает дверь, за которой стоит козел, а не ту, которую вы выбрали, и хост открывает ее. win_or_lose возвращает true или false , обозначая, выиграли ли вы машину или нет, требуется логическое значение «переключатель», которое сообщает, переключили ли вы дверь или нет.
Давайте запустим эту симуляцию 10 миллионов раз:
- Вероятность выигрыша, если вы не переключитесь: 0,334134
- Вероятность выигрыша, если вы переключитесь: 0,667255
Это очень близко к ответам, которые дала нам блок-схема.
На самом деле, чем больше мы запускаем эту симуляцию, тем ближе ответ подходит к истинному значению, тем самым подтверждая закон больших чисел:
То же самое видно из этой таблицы:
| Моделирование выполняется | Вероятность выигрыша, если вы переключитесь | Вероятность выигрыша, если вы не переключитесь |
| 10 | 0,6 | 0,2 |
| 10^2 | 0,63 | 0,33 |
| 10^3 | 0,661 | 0,333 |
| 10^4 | 0,6683 | 0,3236 |
| 10^5 | 0,66762 | 0,33171 |
| 10^6 | 0,667255 | 0,334134 |
| 10^7 | 0,6668756 | 0,3332821 |
Байесовский образ мышления
«Частотист, известный как более классическая версия статистики, предполагает, что вероятность — это долгосрочная частота событий (отсюда и присвоенное название)».
«Байесовская статистика — это теория в области статистики, основанная на байесовской интерпретации вероятности, где вероятность выражает степень доверия к событию. Степень уверенности может быть основана на предварительных знаниях о событии, таких как результаты предыдущих экспериментов, или на личных убеждениях о событии». - из книги "Вероятностное программирование и байесовские методы для хакеров"
Что это значит?
При частотном способе мышления мы рассматриваем вероятности в долгосрочной перспективе. Когда частотник говорит, что вероятность автомобильной аварии составляет 0,001%, это означает, что если мы рассмотрим бесконечные автомобильные поездки, 0,001% из них закончатся аварией.
Байесовское мышление отличается, поскольку мы начинаем с априорного убеждения. Если мы говорим об убеждении 0, это означает, что ваше убеждение состоит в том, что событие никогда не произойдет; и наоборот, убеждение 1 означает, что вы уверены, что это произойдет.
Затем, как только мы начинаем наблюдать за данными, мы обновляем это убеждение, чтобы принять во внимание данные. как нам это сделать? С помощью теоремы Байеса.
Теорема Байеса
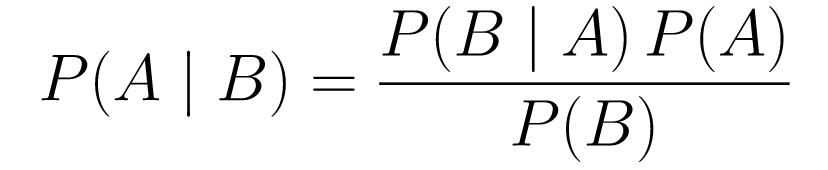 ....(1)
....(1)Давайте сломаем это.
-
P(A | B)дает нам вероятность события A при данном событии B. Это апостериорное значение, B — это данные, которые мы наблюдали, поэтому мы, по сути, говорим, какова вероятность того, что событие произойдет, учитывая данные, которые мы наблюдали. -
P(A)— это априорная оценка, наша вера в то, что событие A произойдет. -
P(B | A)— это вероятность, какова вероятность того, что мы будем наблюдать данные при условии, что A верно.
Давайте рассмотрим пример, скрининговый тест на рак.
Вероятность рака
Допустим, пациентка пришла на маммографию, и маммограмма оказалась положительной. Какова вероятность того, что у пациента действительно рак?
Определим вероятности:
- 1% женщин имеют рак молочной железы.
- Маммография выявляет рак в 80% случаев, когда он действительно присутствует.
- 9,6% маммограмм ложно сообщают, что у вас рак, хотя на самом деле его нет.
Итак, если бы вы сказали, что если маммография даст положительный результат, это означает, что у вас рак с вероятностью 80%, это было бы неправильно. Вы бы не приняли во внимание, что рак – это редкое явление, т.е. что только у 1% женщин есть рак молочной железы. Нам нужно принять это как априорное, и именно здесь вступает в игру теорема Байеса:
Р(С+ | Т+) =(Р(Т+|С+)*Р(С+))/Р(Т+)
-
P(C+ | T+): это вероятность того, что рак есть, при условии, что тест был положительным, это то, что нас интересует. -
P(T+ | C+): это вероятность того, что тест будет положительным, учитывая наличие рака, это, как обсуждалось выше, равно 80% = 0,8. -
P(C+): это априорная вероятность, вероятность наличия у человека рака, равная 1% = 0,01. -
P(T+): это вероятность того, что тест будет положительным, несмотря ни на что, поэтому он состоит из двух компонентов: P(T+) = P(T+|C-) P(C-)+P(T+|C+) P (С+) -
P(T+ | C-): вероятность того, что тест оказался положительным, но рака нет, равна 0,096. -
P(C-): это вероятность отсутствия рака, поскольку вероятность наличия рака составляет 1%, что равно 99% = 0,99. -
P(T+ | C+): это вероятность того, что тест оказался положительным, при условии, что у вас рак, она равна 80% = 0,8. -
P(C+): это вероятность заболевания раком, равная 1% = 0,01.
Подставляем все это в исходную формулу:
Итак, учитывая положительный результат маммографии, вероятность того, что у пациента рак, составляет 7,76%. Сначала это может показаться странным, но в этом есть смысл. Тест дает ложноположительный результат в 9,6% случаев (довольно много), поэтому в данной популяции будет много ложноположительных результатов. Для редкого заболевания большинство положительных результатов теста будут ошибочными.
Давайте теперь вернемся к проблеме Монти Холла и решим ее с помощью теоремы Байеса.
Проблема Монти Холла
Априоры могут быть определены как:
- Предположим, что в начале вы выбрали дверь А.
- Р(Н) = ⅓, ⅓. ⅓ для всех трех дверей, что означает, что до того, как дверь была открыта и козел показался, была равная вероятность того, что машина окажется за любой из них.
Вероятность можно определить как:

-
P(D|H), где событие D состоит в том, что Монти выбирает дверь B и за ней нет машины. -
P(D|H)= 1/2, если машина стоит за дверью A, поскольку вероятность того, что он выберет дверь B, составляет 50 %, а вероятность того, что он выберет дверь C, составляет 50 %. -
P(D|H)= 0, если машина находится за дверью B, поскольку вероятность того, что он выберет дверь B, если машина находится за ней, равна 0%. -
P(D|H)= 1, если машина стоит за C, а вы выбрали A, то есть 100% вероятность того, что он выберет дверь B.
Нас интересует P(H|D) — вероятность того, что машина находится за дверью, при условии, что она показывает нам козу за одной из других дверей.
Из апостериорного значения P(H|D) видно, что переход к двери C из A увеличивает вероятность выигрыша.
Метрополис-Гастингс
Теперь давайте объединим все, что мы уже рассмотрели, и попытаемся понять, как работает Metropolis-Hastings.
Метрополис-Гастингс использует теорему Байеса, чтобы получить апостериорное распределение сложного распределения, из которого выборка напрямую затруднена.
Как? По сути, он случайным образом выбирает разные выборки из пространства и проверяет, является ли новая выборка более вероятной из апостериорной, чем последняя выборка, поскольку мы смотрим на отношение вероятностей P (B) в уравнении (1), получает отменено:
P(принятие) = (P(newSample) * вероятность новой выборки) / (P(oldSample) * вероятность старой выборки)
«Вероятность» каждой новой выборки определяется функцией f . Вот почему f должно быть пропорционально апостериорному значению, из которого мы хотим произвести выборку.
Чтобы решить, следует ли принять или отклонить θ′, для каждого нового предложенного θ’ необходимо вычислить следующее соотношение:
Где θ — старая выборка, P(D| θ) — вероятность выборки θ.
Давайте используем пример, чтобы понять это лучше. Допустим, у вас есть данные, но вы хотите найти нормальное распределение, которое им соответствует, поэтому:
X ~ N (среднее, станд.)
Теперь нам нужно определить априорные значения для среднего и стандартного значений. Для простоты предположим, что оба следуют нормальному распределению со средним значением 1 и стандартным значением 2:
Среднее значение ~ N (1, 2)
станд ~ N(1, 2)
Теперь давайте создадим некоторые данные и предположим, что истинное среднее значение и стандартное значение равны 0,5 и 1,2 соответственно.
import numpy as np import matplotlib.pyplot as plt import scipy.stats as st meanX = 1.5 stdX = 1.2 X = np.random.normal(meanX, stdX, size = 1000) _ = plt.hist(X, bins = 50)PyMC3
Давайте сначала воспользуемся библиотекой PyMC3 для моделирования данных и найдем апостериорное распределение для среднего и стандартного значений.
import pymc3 as pm with pm.Model() as model: mean = pm.Normal("mean", mu = 1, sigma = 2) std = pm.Normal("std", mu = 1, sigma = 2) x = pm.Normal("X", mu = mean, sigma = std, observed = X) step = pm.Metropolis() trace = pm.sample(5000, step = step)Давайте пройдемся по коду.
Во-первых, мы определяем априорное значение для среднего и стандартного значения, т. е. нормаль со средним значением 1 и стандартным значением 2.
x = pm.Normal («X», mu = среднее, sigma = std, наблюдаемое = X)
В этой строке мы определяем интересующую нас переменную; он принимает среднее значение и стандартное значение, которые мы определили ранее, а также наблюдаемые значения, которые мы вычислили ранее.
Посмотрим на результаты:
_ = plt.hist(trace['std'], bins = 50, label = "std") _ = plt.hist(trace['mean'], bins = 50, label = "mean") _ = plt.legend()Стандартное значение сосредоточено вокруг 1,2, а среднее значение составляет 1,55 - довольно близко!
Давайте теперь сделаем это с нуля, чтобы понять Метрополис-Гастингс.
С нуля
Создание предложения
Во-первых, давайте разберемся, чем занимается Metropolis-Hastings. Ранее в этой статье мы говорили: «Metropolis-Hastings случайным образом выбирает разные образцы из пространства», но как он узнает, какой образец выбрать?
Это делается с помощью распределения предложения. Это нормальное распределение с центром в принятой в настоящее время выборке и имеет стандартное отклонение 0,5. Где 0,5 — это гиперпараметр, который мы можем настроить; чем больше STD предложения, тем дальше оно будет искать от принятого в настоящее время образца. Давайте закодируем это.
Поскольку нам нужно найти среднее значение и стандартное значение распределения, эта функция возьмет текущее принятое среднее значение и принятое в настоящее время стандартное значение и вернет предложения для обоих.
def get_proposal(mean_current, std_current, proposal_width = 0.5): return np.random.normal(mean_current, proposal_width), \ np.random.normal(std_current, proposal_width)Принятие/отклонение предложения
Теперь давайте закодируем логику, которая принимает или отклоняет предложение. Он состоит из двух частей: априорной и вероятностной .
Во-первых, давайте посчитаем вероятность того, что предложение придет от априора:
def prior(mean, std, prior_mean, prior_std): return st.norm(prior_mean[0], prior_mean[1]).pdf(mean)* \ st.norm(prior_std[0], prior_std[1]).pdf(std)Он просто берет среднее значение и стандартное значение и вычисляет вероятность того, что это среднее значение и стандартное значение исходят из предыдущего распределения , которое мы определили.
При расчете вероятности мы рассчитываем, насколько вероятно, что данные, которые мы видели, были получены из предложенного распределения.
def likelihood(mean, std, data): return np.prod(st.norm(mean, std).pdf(X))Таким образом, для каждой точки данных мы умножаем вероятность того, что эта точка данных будет получена из предлагаемого распределения.
Теперь нам нужно вызвать эти функции для текущего среднего значения и стандартного значения, а также для предлагаемого среднего значения и стандартного значения .
prior_current = prior(mean_current, std_current, prior_mean, prior_std) likelihood_current = likelihood(mean_current, std_current, data) prior_proposal = prior(mean_proposal, std_proposal, prior_mean, prior_std) likelihood_proposal = likelihood(mean_proposal, std_proposal, data)Весь код:
def accept_proposal(mean_proposal, std_proposal, mean_current, \ std_current, prior_mean, prior_std, data): def prior(mean, std, prior_mean, prior_std): return st.norm(prior_mean[0], prior_mean[1]).pdf(mean)* \ st.norm(prior_std[0], prior_std[1]).pdf(std) def likelihood(mean, std, data): return np.prod(st.norm(mean, std).pdf(X)) prior_current = prior(mean_current, std_current, prior_mean, prior_std) likelihood_current = likelihood(mean_current, std_current, data) prior_proposal = prior(mean_proposal, std_proposal, prior_mean, prior_std) likelihood_proposal = likelihood(mean_proposal, std_proposal, data) return (prior_proposal * likelihood_proposal) / (prior_current * likelihood_current)Теперь давайте создадим последнюю функцию, которая свяжет все вместе и сгенерирует нужные нам апостериорные выборки.
Генерация апостериорной
Теперь мы вызываем функции, которые мы написали выше, и генерируем апостериор!
def get_trace(data, samples = 5000): mean_prior = 1 std_prior = 2 mean_current = mean_prior std_current = std_prior trace = { "mean": [mean_current], "std": [std_current] } for i in tqdm(range(samples)): mean_proposal, std_proposal = get_proposal(mean_current, std_current) acceptance_prob = accept_proposal(mean_proposal, std_proposal, mean_current, \ std_current, [mean_prior, std_prior], \ [mean_prior, std_prior], data) if np.random.rand() < acceptance_prob: mean_current = mean_proposal std_current = std_proposal trace['mean'].append(mean_current) trace['std'].append(std_current) return traceВозможности для совершенствования
Лог твой друг!
Напомним a * b = antilog(log(a) + log(b)) и a / b = antilog(log(a) - log(b)).
Это выгодно для нас, потому что мы будем иметь дело с очень маленькими вероятностями, умножение которых даст ноль, поэтому мы скорее добавим логарифмическую вероятность, проблема решена!
Итак, наш предыдущий код становится:
def accept_proposal(mean_proposal, std_proposal, mean_current, \ std_current, prior_mean, prior_std, data): def prior(mean, std, prior_mean, prior_std): return st.norm(prior_mean[0], prior_mean[1]).logpdf(mean)+ \ st.norm(prior_std[0], prior_std[1]).logpdf(std) def likelihood(mean, std, data): return np.sum(st.norm(mean, std).logpdf(X)) prior_current = prior(mean_current, std_current, prior_mean, prior_std) likelihood_current = likelihood(mean_current, std_current, data) prior_proposal = prior(mean_proposal, std_proposal, prior_mean, prior_std) likelihood_proposal = likelihood(mean_proposal, std_proposal, data) return (prior_proposal + likelihood_proposal) - (prior_current + likelihood_current)Поскольку мы возвращаем журнал вероятности принятия:
if np.random.rand() < acceptance_prob:
Становится:
if math.log(np.random.rand()) < acceptance_prob:
Давайте запустим новый код и построим результаты.
_ = plt.hist(trace['std'], bins = 50, label = "std") _ = plt.hist(trace['mean'], bins = 50, label = "mean") _ = plt.legend()Как видите, стандартное значение равно 1,2, а среднее значение равно 1,5. Мы сделали это!
Двигаться вперед
К настоящему моменту вы, надеюсь, понимаете, как работает Metropolis-Hastings, и вам может быть интересно, где вы можете его использовать.
Что ж, «Байесовские методы для хакеров » — отличная книга, в которой объясняется вероятностное программирование, а если вы хотите узнать больше о теореме Байеса и ее приложениях, « Думай Байес» — отличная книга Аллена Б. Дауни.
Спасибо за чтение, и я надеюсь, что эта статья вдохновит вас открыть для себя удивительный мир байесовской статистики.
