طرق MCMC: Metropolis-Hastings والاستدلال Bayesian
نشرت: 2022-03-11دعنا نحصل على التعريف الأساسي بعيدًا عن الطريق: تتيح لنا طرق Markov Chain Monte Carlo (MCMC) حساب عينات من التوزيع على الرغم من أننا لا نستطيع حسابها.
ماذا يعني هذا؟ دعنا نعود ونتحدث عن عينات مونت كارلو.
أخذ عينات مونت كارلو
ما هي طرق مونت كارلو؟
"طرق مونت كارلو ، أو تجارب مونت كارلو ، هي فئة واسعة من الخوارزميات الحسابية التي تعتمد على أخذ العينات العشوائية المتكررة للحصول على نتائج عددية." (ويكيبيديا)
دعونا نكسر ذلك.
مثال 1: تقدير المساحة
تخيل أن لديك شكلاً غير منتظم ، مثل الشكل الموضح أدناه:
وأنت مكلف بتحديد المساحة التي يحيط بها هذا الشكل. إحدى الطرق التي يمكنك استخدامها هي عمل مربعات صغيرة في الشكل ، وعد المربعات ، وهذا سيعطيك تقريبًا دقيقًا جدًا للمنطقة. ومع ذلك ، هذا صعب ويستغرق وقتا طويلا.
أخذ عينات مونت كارلو للإنقاذ!
أولاً ، نرسم مربعًا كبيرًا لمساحة معروفة حول الشكل ، على سبيل المثال 50 سم 2. الآن "نعلق" هذا المربع ونبدأ في رمي السهام بشكل عشوائي على الشكل.
بعد ذلك ، نحسب العدد الإجمالي للسهام في المستطيل وعدد السهام في الشكل الذي نهتم به. لنفترض أن إجمالي عدد "السهام" المستخدمة كان 100 وأن 22 منها انتهى بها الأمر داخل الشكل. الآن يمكن حساب المنطقة بالصيغة البسيطة:
مساحة الشكل = مساحة المربع * (عدد السهام في الشكل) / (عدد السهام في المربع)
لذلك ، في حالتنا ، هذا يعود إلى:
مساحة الشكل = 50 * 22/100 = 11 سم 2
إذا ضربنا عدد "السهام" في عامل 10 ، يصبح هذا التقريب قريبًا جدًا من الإجابة الحقيقية:
مساحة الشكل = 50 * 280/1000 = 14 سم 2
هذه هي الطريقة التي نقسم بها المهام المعقدة ، مثل تلك المذكورة أعلاه ، باستخدام عينات مونت كارلو.
قانون الأعداد الكبيرة
كان تقريب المنطقة أقرب كلما ألقينا المزيد من السهام ، وهذا بسبب قانون الأعداد الكبيرة:
قانون الأعداد الكبيرة هو نظرية تصف نتيجة إجراء نفس التجربة عددًا كبيرًا من المرات. وفقًا للقانون ، يجب أن يكون متوسط النتائج التي تم الحصول عليها من عدد كبير من التجارب قريبًا من القيمة المتوقعة ، وسوف يميل إلى الاقتراب كلما تم إجراء المزيد من التجارب ".
يقودنا هذا إلى مثالنا التالي ، مشكلة مونتي هول الشهيرة.
مثال 2: مشكلة مونتي هول
مشكلة مونتي هول هي دعابة دماغ مشهورة جدا:
"هناك ثلاثة أبواب ، أحدها خلفه سيارة ، والأخرى خلفها ماعز. تختار بابًا ، يفتح المضيف بابًا مختلفًا ويظهر لك وجود عنزة خلفه. ثم يسألك عما إذا كنت تريد تغيير قرارك. هل؟ لماذا ا؟ لما لا؟"
أول ما يتبادر إلى ذهنك هو أن فرص الفوز متساوية سواء قمت بالتبديل أم لا ، لكن هذا ليس صحيحًا. لنقم بعمل مخطط انسيابي بسيط لتوضيح ذلك.
بافتراض أن السيارة خلف الباب رقم 3:
وبالتالي ، إذا قمت بالتبديل ، فستكسب مرة ، وإذا لم تقم بالتبديل ، فستربح ⅓ مرة فقط.
دعنا نحل هذا باستخدام أخذ العينات.
wins = [] for i in range(int(10e6)): car_door = assign_car_door() choice = random.randint(0, 2) opened_door = assign_door_to_open(car_door) did_he_win = win_or_lose(choice, car_door, opened_door, switch = False) wins.append(did_he_win) print(sum(wins)/len(wins)) إن وظيفة assign_car_door() هي مجرد مولد أرقام عشوائي يختار الباب 0 أو 1 أو 2 خلفه توجد سيارة. يؤدي استخدام assign_door_to_open إلى تحديد باب به تيس خلفه وليس الباب الذي حددته ، ويفتحه المضيف. يُرجع win_or_lose أو خطأً ، مشيرًا إلى ما إذا كنت قد فزت بالسيارة أم لا ، فإنه يأخذ "مفتاحًا" منطقيًا يوضح ما إذا كنت قد قمت بتبديل الباب أم لا.
لنجري هذه المحاكاة 10 ملايين مرة:
- احتمالية الفوز إذا لم تقم بالتبديل: 0.334134
- احتمالية الفوز إذا قمت بالتبديل: 0.667255
هذا قريب جدًا من الإجابات التي قدمها لنا المخطط الانسيابي.
في الواقع ، كلما قمنا بتشغيل هذه المحاكاة ، كلما اقتربت الإجابة من القيمة الحقيقية ، وبالتالي التحقق من صحة قانون الأعداد الكبيرة:
يمكن رؤية الشيء نفسه من هذا الجدول:
| تشغيل المحاكاة | احتمالية الفوز إذا قمت بالتبديل | احتمالية الفوز إذا لم تقم بالتبديل |
| 10 | 0.6 | 0.2 |
| 10 ^ 2 | 0.63 | 0.33 |
| 10 ^ 3 | 0.661 | 0.333 |
| 10 ^ 4 | 0.6683 | 0.3236 |
| 10 ^ 5 | 0.66762 | 0.33171 |
| 10 ^ 6 | 0.667255 | 0.334134 |
| 10 ^ 7 | 0.6668756 | 0.3332821 |
طريقة التفكير بايزي
"المتكرر ، المعروف باسم الإصدار الأكثر كلاسيكية للإحصاءات ، يفترض أن الاحتمال هو تكرار الأحداث على المدى الطويل (ومن ثم العنوان الممنوح)."
إحصائيات بايز هي نظرية في مجال الإحصاء تعتمد على تفسير بايزي للاحتمال حيث يعبر الاحتمال عن درجة من الاعتقاد في حدث ما. قد تستند درجة الاعتقاد إلى معرفة مسبقة بالحدث ، مثل نتائج التجارب السابقة أو المعتقدات الشخصية حول الحدث ". - من البرمجة الاحتمالية والطرق البايزية للقراصنة
ماذا يعني هذا؟
في طريقة التفكير المتكررة ، ننظر إلى الاحتمالات على المدى الطويل. عندما يقول متكرر أن هناك احتمال بنسبة 0.001٪ لحدوث حادث سيارة ، فهذا يعني أنه إذا أخذنا في الاعتبار رحلات السيارات اللانهائية ، فإن 0.001٪ منها سينتهي في حادث.
تختلف عقلية بايزي ، حيث نبدأ باعتقاد سابق. إذا تحدثنا عن اعتقاد بـ 0 ، فهذا يعني أن إيمانك هو أن الحدث لن يحدث أبدًا ؛ على العكس من ذلك ، فإن الاعتقاد بـ 1 يعني أنك متأكد من حدوث ذلك.
بعد ذلك ، بمجرد أن نبدأ في مراقبة البيانات ، نقوم بتحديث هذا الاعتقاد لأخذ البيانات في الاعتبار. كيف نفعل ذلك؟ باستخدام نظرية بايز.
مبرهنة بايز
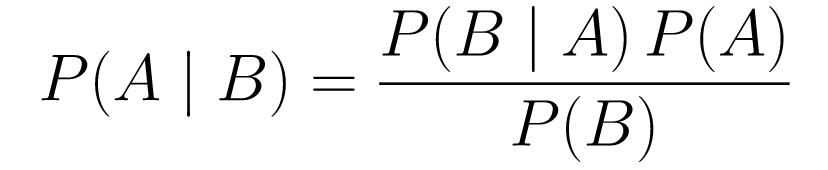 .... (1)
.... (1)دعونا نكسرها.
- يعطينا
P(A | B)احتمالية وقوع حدث A معطى B. هذا هو الحدث الخلفي ، B هو البيانات التي لاحظناها ، لذلك فنحن نقول أساسًا ما هو احتمال حدوث حدث ، مع الأخذ في الاعتبار البيانات التي لاحظناها. -
P(A)هي السابقة ، إيماننا بأن الحدث A سيحدث. -
P(B | A)هو الاحتمال ، ما هو احتمال أن نلاحظ البيانات بالنظر إلى أن A صحيح.
لنلق نظرة على مثال ، اختبار فحص السرطان.
احتمالية الإصابة بالسرطان
لنفترض أن المريضة تذهب لإجراء تصوير الثدي بالأشعة السينية ، ويعود التصوير الشعاعي للثدي بشكل إيجابي. ما هو احتمال أن يكون المريض مصابًا بالفعل بالسرطان؟
دعنا نحدد الاحتمالات:
- 1٪ من النساء مصابات بسرطان الثدي.
- يكتشف تصوير الثدي بالأشعة السينية السرطان في 80٪ من الوقت عندما يكون موجودًا بالفعل.
- تشير 9.6٪ من صور الثدي بالأشعة السينية بشكل خاطئ إلى إصابتك بالسرطان في حين أنك لا تعانين منه بالفعل.
لذا ، إذا كنت ستقول أنه إذا كان تصوير الثدي بالأشعة السينية إيجابيًا مما يعني أن هناك فرصة بنسبة 80٪ للإصابة بالسرطان ، فسيكون ذلك خطأ. لن تأخذ في الاعتبار أن الإصابة بالسرطان هي حدث نادر ، أي أن 1٪ فقط من النساء مصابات بسرطان الثدي. نحتاج أن نأخذ هذا على النحو السابق ، وهنا يأتي دور نظرية بايز:
الفوسفور (C + | T +) = (P (T + | C +) * P (C +)) / P (T +)
-
P(C+ | T+): هذا هو احتمال وجود السرطان ، بالنظر إلى أن الاختبار كان إيجابيًا ، وهذا ما نهتم به. -
P(T+ | C+): هذا هو احتمال أن يكون الاختبار إيجابيًا ، نظرًا لوجود سرطان ، وهذا ، كما نوقش أعلاه ، يساوي 80٪ = 0.8. -
P(C+): هذا هو الاحتمال السابق ، احتمال إصابة الفرد بالسرطان ، والذي يساوي 1٪ = 0.01. -
P(T+): هذا هو احتمال أن يكون الاختبار إيجابيًا ، بغض النظر عن أي شيء ، لذلك يتكون من مكونين: P (T +) = P (T + | C-) P (C -) + P (T + | C +) P (ج +) -
P(T+ | C-): هذا هو احتمال أن الاختبار جاء إيجابيًا ولكن لا يوجد سرطان ، وهذا معطى بنسبة 0.096. -
P(C-): هذا هو احتمال عدم الإصابة بالسرطان حيث أن احتمال الإصابة بالسرطان هو 1٪ ، وهذا يساوي 99٪ = 0.99. -
P(T+ | C+): هذا هو احتمال أن الاختبار جاء إيجابيًا ، بالنظر إلى إصابتك بالسرطان ، فهذا يساوي 80٪ = 0.8. -
P(C+): هذا هو احتمال الإصابة بالسرطان ، والذي يساوي 1٪ = 0.01.
بإدخال كل هذا في الصيغة الأصلية:
لذلك ، بالنظر إلى أن صورة الماموجرام جاءت إيجابية ، فهناك احتمال بنسبة 7.76٪ أن يصاب المريض بالسرطان. قد يبدو غريباً في البداية ولكنه منطقي. يعطي الاختبار نسبة إيجابية خاطئة تبلغ 9.6٪ من الوقت (عالية جدًا) ، لذلك سيكون هناك العديد من الإيجابيات الكاذبة في مجموعة سكانية معينة. بالنسبة لمرض نادر ، ستكون معظم نتائج الاختبارات الإيجابية خاطئة.
دعونا الآن نعيد النظر في مشكلة مونتي هول ونحلها باستخدام نظرية بايز.
مشكلة مونتي هول
يمكن تعريف المقدمات على النحو التالي:
- افترض أنك اخترت الباب أ كاختيارك في البداية.
- الفوسفور (ح) = ، ⅓. ⅓ بالنسبة للأبواب الثلاثة ، مما يعني أنه قبل فتح الباب وكشف العنزة ، كانت هناك فرصة متساوية لوجود السيارة خلف أي منها.
يمكن تعريف الاحتمالية على النحو التالي:

-
P(D|H)، حيث يكون الحدث D هو أن مونتي يختار الباب B ولا توجد سيارة خلفه. -
P(D|H)= 1/2 إذا كانت السيارة خلف الباب A - حيث توجد فرصة بنسبة 50٪ لاختيار الباب B و 50٪ أن يختار الباب C. -
P(D|H)= 0 إذا كانت السيارة خلف الباب B ، حيث توجد فرصة بنسبة 0٪ لاختيار الباب B إذا كانت السيارة خلفه. -
P(D|H)= 1 إذا كانت السيارة خلف C ، واخترت A ، فهناك احتمال 100٪ أنه سيختار الباب B.
نحن مهتمون P(H|D) ، وهي احتمالية أن تكون السيارة خلف أحد الأبواب نظرًا لأنه يظهر لنا عنزة خلف أحد الأبواب الأخرى.
يمكن أن نرى من الجزء الخلفي ، P(H|D) ، أن التبديل إلى الباب C من A سيزيد من احتمالية الفوز.
متروبوليس-هاستينغز
الآن ، دعنا نجمع كل ما غطيناه حتى الآن ونحاول فهم كيفية عمل Metropolis-Hastings.
تستخدم Metropolis-Hastings نظرية بايز للحصول على التوزيع اللاحق لتوزيع معقد ، والذي يصعب منه أخذ العينات مباشرة.
كيف؟ بشكل أساسي ، يختار عشوائيًا عينات مختلفة من مساحة ويتحقق مما إذا كانت العينة الجديدة أكثر احتمالًا أن تكون من العينة الأخيرة ، نظرًا لأننا ننظر إلى نسبة الاحتمالات ، يحصل P (B) في المعادلة (1) تم إلغاؤها:
P (القبول) = (P (newSample) * احتمال وجود عينة جديدة) / (P (oldSample) * احتمال وجود عينة قديمة)
تحدد الوظيفة f "احتمالية" كل عينة جديدة. لهذا السبب يجب أن تكون f متناسبة مع المؤخرة التي نريد أخذ عينات منها.
لتحديد ما إذا كان سيتم قبول أو رفض θ ′ ، يجب حساب النسبة التالية لكل 'جديد مقترح:
حيث θ هي العينة القديمة ، P(D| θ) هو احتمال العينة θ.
دعنا نستخدم مثالاً لفهم هذا بشكل أفضل. لنفترض أن لديك بيانات ولكنك تريد معرفة التوزيع الطبيعي الذي يناسبها ، لذلك:
X ~ N (يعني ، الأمراض المنقولة جنسياً)
الآن نحن بحاجة إلى تحديد المقدمات للمتوسط والأمراض المنقولة جنسياً على حد سواء. للتبسيط ، سنفترض أن كلاهما يتبع التوزيع الطبيعي بمتوسط 1 و 2 القياسي:
يعني ~ N (1 ، 2)
الأمراض المنقولة جنسيًا ~ N (1 ، 2)
الآن ، دعنا ننشئ بعض البيانات ونفترض أن المتوسط الحقيقي والأمراض المنقولة جنسياً هما 0.5 و 1.2 على التوالي.
import numpy as np import matplotlib.pyplot as plt import scipy.stats as st meanX = 1.5 stdX = 1.2 X = np.random.normal(meanX, stdX, size = 1000) _ = plt.hist(X, bins = 50)PyMC3
دعنا أولاً نستخدم مكتبة تسمى PyMC3 لنمذجة البيانات والعثور على التوزيع اللاحق للمتوسط والأمراض المنقولة جنسياً.
import pymc3 as pm with pm.Model() as model: mean = pm.Normal("mean", mu = 1, sigma = 2) std = pm.Normal("std", mu = 1, sigma = 2) x = pm.Normal("X", mu = mean, sigma = std, observed = X) step = pm.Metropolis() trace = pm.sample(5000, step = step)دعنا ننتقل إلى الكود.
أولاً ، نحدد السابق للمتوسط والأمراض المنقولة جنسياً ، أي عادي بمتوسط 1 و 2 قياسي.
x = pm.Normal (“X” ، mu = متوسط ، سيجما = الأمراض المنقولة جنسياً ، ملحوظة = X)
في هذا السطر ، نحدد المتغير الذي نهتم به ؛ يأخذ المتوسط و القياسي الذي حددناه سابقًا ، كما أنه يأخذ القيم المرصودة التي حسبناها سابقًا.
لنلقِ نظرة على النتائج:
_ = plt.hist(trace['std'], bins = 50, label = "std") _ = plt.hist(trace['mean'], bins = 50, label = "mean") _ = plt.legend()يتمركز std حول 1.2 ، والمتوسط عند 1.55 - قريب جدًا!
لنفعل ذلك الآن من الصفر لفهم متروبوليس-هاستينغز.
من سكراتش
توليد اقتراح
أولاً ، دعنا نفهم ما يفعله متروبوليس-هاستينغز. في وقت سابق من هذا المقال ، قلنا ، "تختار Metropolis-Hastings عينات مختلفة عشوائيًا من مساحة ما ،" ولكن كيف تعرف أي عينة تختار؟
يفعل ذلك باستخدام توزيع الاقتراح. إنه توزيع طبيعي يتمحور حول العينة المقبولة حاليًا وله STD 0.5. حيث 0.5 هو hyperparameter ، يمكننا تعديل ؛ كلما زاد عدد STD الخاص بالمقترح ، زاد البحث من العينة المقبولة حاليًا. دعونا نبرمج هذا.
نظرًا لأنه يتعين علينا العثور على المتوسط والأرقام القياسية للتوزيع ، فستأخذ هذه الوظيفة الوسيط المقبول حاليًا والأرقام القياسية المقبولة حاليًا ، وستقوم بإرجاع المقترحات لكليهما.
def get_proposal(mean_current, std_current, proposal_width = 0.5): return np.random.normal(mean_current, proposal_width), \ np.random.normal(std_current, proposal_width)قبول / رفض اقتراح
الآن ، دعنا نبرمج المنطق الذي يقبل الاقتراح أو يرفضه. ويتكون من جزأين: السابق والاحتمالية .
أولاً ، دعنا نحسب احتمال أن يأتي الاقتراح من السابق:
def prior(mean, std, prior_mean, prior_std): return st.norm(prior_mean[0], prior_mean[1]).pdf(mean)* \ st.norm(prior_std[0], prior_std[1]).pdf(std)إنه يأخذ فقط المتوسط والأمراض المنقولة جنسياً ويحسب مدى احتمالية أن يأتي هذا المتوسط والأمراض المنقولة جنسياً من التوزيع السابق الذي حددناه.
عند حساب الاحتمالية ، نحسب مدى احتمالية أن البيانات التي رأيناها جاءت من التوزيع المقترح.
def likelihood(mean, std, data): return np.prod(st.norm(mean, std).pdf(X))لذلك لكل نقطة بيانات ، نقوم بضرب احتمال أن تأتي نقطة البيانات من التوزيع المقترح.
الآن ، نحتاج إلى استدعاء هاتين الدالتين للمتوسط الحالي والأمراض المنقولة جنسياً وللمتوسط والأمراض المنقولة جنسياً المقترحين.
prior_current = prior(mean_current, std_current, prior_mean, prior_std) likelihood_current = likelihood(mean_current, std_current, data) prior_proposal = prior(mean_proposal, std_proposal, prior_mean, prior_std) likelihood_proposal = likelihood(mean_proposal, std_proposal, data)الكود كله:
def accept_proposal(mean_proposal, std_proposal, mean_current, \ std_current, prior_mean, prior_std, data): def prior(mean, std, prior_mean, prior_std): return st.norm(prior_mean[0], prior_mean[1]).pdf(mean)* \ st.norm(prior_std[0], prior_std[1]).pdf(std) def likelihood(mean, std, data): return np.prod(st.norm(mean, std).pdf(X)) prior_current = prior(mean_current, std_current, prior_mean, prior_std) likelihood_current = likelihood(mean_current, std_current, data) prior_proposal = prior(mean_proposal, std_proposal, prior_mean, prior_std) likelihood_proposal = likelihood(mean_proposal, std_proposal, data) return (prior_proposal * likelihood_proposal) / (prior_current * likelihood_current)الآن ، لنقم بإنشاء الوظيفة النهائية التي ستربط كل شيء معًا وتولد العينات اللاحقة التي نحتاجها.
توليد المؤخرة
الآن ، نسمي الوظائف التي كتبناها أعلاه وننشئ اللاحقة!
def get_trace(data, samples = 5000): mean_prior = 1 std_prior = 2 mean_current = mean_prior std_current = std_prior trace = { "mean": [mean_current], "std": [std_current] } for i in tqdm(range(samples)): mean_proposal, std_proposal = get_proposal(mean_current, std_current) acceptance_prob = accept_proposal(mean_proposal, std_proposal, mean_current, \ std_current, [mean_prior, std_prior], \ [mean_prior, std_prior], data) if np.random.rand() < acceptance_prob: mean_current = mean_proposal std_current = std_proposal trace['mean'].append(mean_current) trace['std'].append(std_current) return traceمجال للتحسين
السجل هو صديقك!
أذكر a * b = antilog(log(a) + log(b)) و a / b = antilog(log(a) - log(b)).
هذا مفيد لنا لأننا سنتعامل مع احتمالات صغيرة جدًا ، يتم الضرب فيها مما ينتج عنه صفر ، لذلك نضيف بدلاً من ذلك مشكلة السجل ، المشكلة التي تم حلها!
لذلك ، يصبح الكود السابق لدينا:
def accept_proposal(mean_proposal, std_proposal, mean_current, \ std_current, prior_mean, prior_std, data): def prior(mean, std, prior_mean, prior_std): return st.norm(prior_mean[0], prior_mean[1]).logpdf(mean)+ \ st.norm(prior_std[0], prior_std[1]).logpdf(std) def likelihood(mean, std, data): return np.sum(st.norm(mean, std).logpdf(X)) prior_current = prior(mean_current, std_current, prior_mean, prior_std) likelihood_current = likelihood(mean_current, std_current, data) prior_proposal = prior(mean_proposal, std_proposal, prior_mean, prior_std) likelihood_proposal = likelihood(mean_proposal, std_proposal, data) return (prior_proposal + likelihood_proposal) - (prior_current + likelihood_current)بما أننا نعيد سجل احتمالية القبول:
if np.random.rand() < acceptance_prob:
يصبح:
if math.log(np.random.rand()) < acceptance_prob:
لنقم بتشغيل الكود الجديد ونرسم النتائج.
_ = plt.hist(trace['std'], bins = 50, label = "std") _ = plt.hist(trace['mean'], bins = 50, label = "mean") _ = plt.legend()كما ترى ، فإن std يتركز عند 1.2 ، والمتوسط عند 1.5. لقد فعلناها!
تحرك للأمام
الآن ، نأمل أن تفهم كيف تعمل Metropolis-Hastings وقد تتساءل أين يمكنك استخدامها.
حسنًا ، يعد كتاب Bayesian Methods for Hackers كتابًا ممتازًا يشرح البرمجة الاحتمالية ، وإذا كنت تريد معرفة المزيد عن نظرية بايز وتطبيقاتها ، فإن Think Bayes هو كتاب رائع من تأليف Allen B.
شكرًا على القراءة ، وآمل أن يشجعك هذا المقال على اكتشاف العالم المذهل لإحصائيات Bayesian.
