Metode MCMC: Metropolis-Hastings și Inferența Bayesiană
Publicat: 2022-03-11Să scoatem din cale definiția de bază: metodele Markov Chain Monte Carlo (MCMC) ne permit să calculăm mostre dintr-o distribuție, chiar dacă nu o putem calcula.
Ce inseamna asta? Să revenim și să vorbim despre Monte Carlo Sampling.
Eșantionarea Monte Carlo
Care sunt metodele Monte Carlo?
„Metodele Monte Carlo, sau experimentele Monte Carlo, sunt o clasă largă de algoritmi de calcul care se bazează pe eșantionarea aleatorie repetată pentru a obține rezultate numerice.” (Wikipedia)
Să descompun asta.
Exemplul 1: Estimarea zonei
Imaginați-vă că aveți o formă neregulată, ca forma prezentată mai jos:
Și aveți sarcina de a determina zona cuprinsă de această formă. Una dintre metodele pe care le puteți folosi este să faceți pătrate mici în formă, să numărați pătratele și asta vă va oferi o aproximare destul de precisă a zonei. Cu toate acestea, este dificil și necesită timp.
Monte Carlo prelevare de probe pentru salvare!
Mai întâi, desenăm un pătrat mare cu o zonă cunoscută în jurul formei, de exemplu de 50 cm2. Acum „atârnăm” acest pătrat și începem să aruncăm săgeți aleatoriu în formă.
Apoi, numărăm numărul total de săgeți din dreptunghi și numărul de săgeți din forma care ne interesează. Să presupunem că numărul total de săgeți utilizate a fost 100 și că 22 dintre ele au ajuns în formă. Acum aria poate fi calculată prin formula simplă:
aria formei = aria pătratului *(numărul de săgeți în formă) / (numărul de săgeți în pătrat)
Deci, în cazul nostru, aceasta se reduce la:
aria formei = 50 * 22/100 = 11 cm2
Dacă înmulțim numărul de „săgeți” cu un factor de 10, această aproximare devine foarte aproape de răspunsul real:
aria formei = 50 * 280/1000 = 14 cm2
Acesta este modul în care defalcăm sarcinile complicate, precum cea prezentată mai sus, utilizând eșantionarea Monte Carlo.
Legea numerelor mari
Aproximația zonei a fost mai apropiată cu cât aruncam mai multe săgeți, iar acest lucru se datorează Legii numerelor mari:
„Legea numerelor mari este o teoremă care descrie rezultatul efectuării aceluiași experiment de un număr mare de ori. Potrivit legii, media rezultatelor obținute dintr-un număr mare de încercări ar trebui să fie apropiată de valoarea așteptată și va tinde să se apropie pe măsură ce se efectuează mai multe încercări.”
Acest lucru ne duce la următorul nostru exemplu, celebra problemă Monty Hall.
Exemplul 2: Problema Monty Hall
Problema Monty Hall este un teaser foarte faimos:
„Sunt trei uși, una are o mașină în spate, celelalte au o capră în spate. Alegeți o ușă, gazda deschide o altă ușă și vă arată că în spatele ei este o capră. Apoi te întreabă dacă vrei să-ți schimbi decizia. Tu? De ce? De ce nu?"
Primul lucru care îți vine în minte este că șansele de a câștiga sunt egale indiferent dacă schimbi sau nu, dar nu este adevărat. Să facem o diagramă simplă pentru a demonstra același lucru.
Presupunând că mașina se află în spatele ușii 3:
Prin urmare, dacă schimbi, câștigi de ⅔ ori, iar dacă nu schimbi, câștigi doar de ⅓ ori.
Să rezolvăm acest lucru folosind eșantionarea.
wins = [] for i in range(int(10e6)): car_door = assign_car_door() choice = random.randint(0, 2) opened_door = assign_door_to_open(car_door) did_he_win = win_or_lose(choice, car_door, opened_door, switch = False) wins.append(did_he_win) print(sum(wins)/len(wins)) Funcția assign_car_door() este doar un generator de numere aleatorii care selectează o ușă 0, 1 sau 2, în spatele căreia se află o mașină. Folosind assign_door_to_open selectează o ușă care are o capră în spate și nu este cea pe care ai selectat-o, iar gazda o deschide. win_or_lose returnează true sau false , indicând dacă ați câștigat mașina sau nu, este nevoie de un „comutator” bool care spune dacă ați schimbat ușa sau nu.
Să rulăm această simulare de 10 milioane de ori:
- Probabilitatea de a câștiga dacă nu schimbați: 0,334134
- Probabilitatea de a câștiga dacă schimbați: 0,667255
Acest lucru este foarte aproape de răspunsurile pe care ni le-a dat diagrama.
De fapt, cu cât rulăm mai mult această simulare, cu atât răspunsul se apropie de valoarea adevărată, validând astfel legea numerelor mari:
Același lucru se poate observa din acest tabel:
| Se rulează simulări | Probabilitatea de a câștiga dacă schimbați | Probabilitatea de a câștiga dacă nu schimbați |
| 10 | 0,6 | 0,2 |
| 10^2 | 0,63 | 0,33 |
| 10^3 | 0,661 | 0,333 |
| 10^4 | 0,6683 | 0,3236 |
| 10^5 | 0,66762 | 0,33171 |
| 10^6 | 0,667255 | 0,334134 |
| 10^7 | 0,6668756 | 0,3332821 |
Modul Bayesian de gândire
„Frequentistul, cunoscut ca versiunea mai clasică a statisticilor, presupune că probabilitatea este frecvența pe termen lung a evenimentelor (de unde titlul acordat).”
„Statistica bayesiană este o teorie în domeniul statisticii bazată pe interpretarea bayesiană a probabilității, în care probabilitatea exprimă un grad de credință într-un eveniment. Gradul de credință se poate baza pe cunoștințele anterioare despre eveniment, cum ar fi rezultatele experimentelor anterioare, sau pe convingerile personale despre eveniment.” - din Programare probabilistică și Metode bayesiene pentru hackeri
Ce inseamna asta?
În modul de gândire frecventist, ne uităm la probabilități pe termen lung. Când un frecventist spune că există o șansă de 0,001% ca un accident de mașină să se întâmple, înseamnă că, dacă luăm în considerare călătoriile infinite cu mașina, 0,001% dintre ele se vor termina într-un accident.
O mentalitate bayesiană este diferită, deoarece începem cu un antecedent, o credință. Dacă vorbim despre o credință de 0, înseamnă că credința ta este că evenimentul nu se va întâmpla niciodată; invers, o credință de 1 înseamnă că ești sigur că se va întâmpla.
Apoi, odată ce începem să observăm datele, actualizăm această convingere pentru a lua în considerare datele. Cum facem asta? Folosind teorema Bayes.
Teorema Bayes
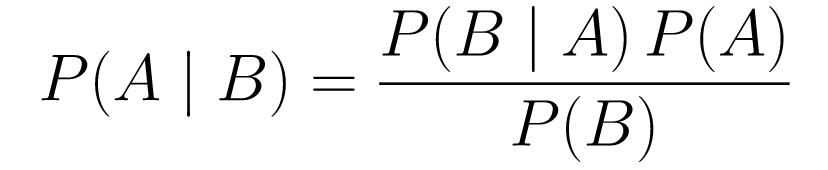 ....(1)
....(1)Să-l descompunem.
-
P(A | B)ne oferă probabilitatea evenimentului A dat evenimentul B. Acesta este posterior, B este datele pe care le-am observat, deci spunem în esență care este probabilitatea ca un eveniment să se întâmple, având în vedere datele pe care le-am observat. -
P(A)este priorul, convingerea noastră că evenimentul A se va întâmpla. -
P(B | A)este probabilitatea, care este probabilitatea ca să observăm datele având în vedere că A este adevărată.
Să ne uităm la un exemplu, testul de depistare a cancerului.
Probabilitatea de cancer
Să presupunem că un pacient merge să facă o mamografie, iar mamografia este pozitivă. Care este probabilitatea ca pacientul să aibă de fapt cancer?
Să definim probabilitățile:
- 1% dintre femei au cancer de sân.
- Mamografiile depistează cancerul în 80% din timp când acesta este de fapt prezent.
- 9,6% dintre mamografii raportează în mod fals că aveți cancer atunci când de fapt nu îl aveți.
Deci, dacă ar fi să spuneți că dacă o mamografie a revenit pozitiv, ceea ce înseamnă că există o șansă de 80% să aveți cancer, ar fi greșit. Nu ai lua în considerare faptul că a avea cancer este un eveniment rar, adică doar 1% dintre femei au cancer de sân. Trebuie să luăm acest lucru ca anterior și aici intră în joc teorema Bayes:
P(C+ | T+) =(P(T+|C+)*P(C+))/P(T+)
-
P(C+ | T+): Aceasta este probabilitatea ca cancerul să fie acolo, având în vedere că testul a fost pozitiv, acesta este ceea ce ne interesează. -
P(T+ | C+): Aceasta este probabilitatea ca testul să fie pozitiv, având în vedere că există cancer, acesta, așa cum sa discutat mai sus, este egal cu 80% = 0,8. -
P(C+): Aceasta este probabilitatea anterioară, probabilitatea ca un individ să aibă cancer, care este egală cu 1% = 0,01. -
P(T+): Aceasta este probabilitatea ca testul să fie pozitiv, indiferent de ce, deci are două componente: P(T+) = P(T+|C-) P(C-)+P(T+|C+) P (C+) -
P(T+ | C-): Aceasta este probabilitatea ca testul să fie pozitiv, dar nu există cancer, aceasta este dată de 0,096. -
P(C-): Aceasta este probabilitatea de a nu avea cancer, deoarece probabilitatea de a avea cancer este de 1%, aceasta este egală cu 99% = 0,99. -
P(T+ | C+): Aceasta este probabilitatea ca testul să fie pozitiv, având în vedere că aveți cancer, aceasta este egală cu 80% = 0,8. -
P(C+): Aceasta este probabilitatea de a avea cancer, care este egală cu 1% = 0,01.
Conectând toate acestea în formula originală:
Deci, având în vedere că mamografia a revenit pozitiv, există o șansă de 7,76% ca pacientul să aibă cancer. Poate părea ciudat la început, dar are sens. Testul dă un fals pozitiv în 9,6% din timp (destul de mare), așa că vor exista multe fals pozitive într-o anumită populație. Pentru o boală rară, majoritatea rezultatelor pozitive ale testelor vor fi greșite.
Să revizuim acum problema lui Monty Hall și să o rezolvăm folosind teorema Bayes.
Problema Monty Hall
Precedentele pot fi definite ca:

- Să presupunem că alegeți ușa A ca alegere la început.
- P(H) = ⅓, ⅓. ⅓ pentru toate cele trei uși, ceea ce înseamnă că înainte ca ușa să fie deschisă și capra dezvăluită, existau șanse egale ca mașina să fie în spatele oricăreia dintre ele.
Probabilitatea poate fi definită astfel:
-
P(D|H), unde evenimentul D este că Monty alege ușa B și nu există nicio mașină în spatele ei. -
P(D|H)= 1/2 dacă mașina se află în spatele ușii A - deoarece există o șansă de 50% ca el să aleagă ușa B și șanse de 50% să aleagă ușa C. -
P(D|H)= 0 dacă mașina se află în spatele ușii B, deoarece există o șansă de 0% ca el să aleagă ușa B dacă mașina se află în spatele ei. -
P(D|H)= 1 dacă mașina este în spatele lui C și alegeți A, există o probabilitate de 100% ca el să aleagă ușa B.
Ne interesează P(H|D) , care este probabilitatea ca mașina să fie în spatele unei uși, având în vedere că ne arată o capră în spatele uneia dintre celelalte uși.
Se poate observa din partea posterioară, P(H|D) , că trecerea la ușa C de la A va crește probabilitatea de câștig.
Metropolis-Hastings
Acum, să combinăm tot ce am abordat până acum și să încercăm să înțelegem cum funcționează Metropolis-Hastings.
Metropolis-Hastings folosește teorema Bayes pentru a obține distribuția posterioară a unei distribuții complexe, din care eșantionarea directă este dificilă.
Cum? În esență, selectează aleatoriu diferite eșantioane dintr-un spațiu și verifică dacă noul eșantion este mai probabil să fie din eșantion posterior decât ultimul, deoarece ne uităm la raportul de probabilități, P(B) în ecuația (1), obține anulat:
P(acceptare) = ( P(newSample) * Probabilitatea unui eșantion nou) / (P(oldSample) * Probabilitatea unui eșantion vechi)
„Versibilitatea” fiecărui eșantion nou este decisă de funcția f . De aceea f trebuie să fie proporțional cu posteriorul din care vrem să prelevăm.
Pentru a decide dacă θ′ trebuie să fie acceptat sau respins, trebuie calculat următorul raport pentru fiecare nou θ' propus:
Unde θ este eșantionul vechi, P(D| θ) este probabilitatea eșantionului θ.
Să folosim un exemplu pentru a înțelege mai bine acest lucru. Să presupunem că aveți date, dar doriți să aflați distribuția normală care se potrivește, deci:
X ~ N(medie, std)
Acum trebuie să definim prioritățile pentru ambele medii și std. Pentru simplitate, vom presupune că ambele urmează o distribuție normală cu medie 1 și std 2:
Media ~ N(1, 2)
std ~ N(1, 2)
Acum, să generăm câteva date și să presupunem că adevărata medie și std sunt 0,5 și, respectiv, 1,2.
import numpy as np import matplotlib.pyplot as plt import scipy.stats as st meanX = 1.5 stdX = 1.2 X = np.random.normal(meanX, stdX, size = 1000) _ = plt.hist(X, bins = 50)PyMC3
Să folosim mai întâi o bibliotecă numită PyMC3 pentru a modela datele și pentru a găsi distribuția posterioară pentru medie și std.
import pymc3 as pm with pm.Model() as model: mean = pm.Normal("mean", mu = 1, sigma = 2) std = pm.Normal("std", mu = 1, sigma = 2) x = pm.Normal("X", mu = mean, sigma = std, observed = X) step = pm.Metropolis() trace = pm.sample(5000, step = step)Să trecem peste cod.
În primul rând, definim priorul pentru medie și std, adică o normală cu media 1 și std 2.
x = pm.Normal(“X”, mu = medie, sigma = std, observat = X)
În această linie, definim variabila care ne interesează; ia media și std pe care le-am definit mai devreme, ia și valorile observate pe care le-am calculat mai devreme.
Să ne uităm la rezultate:
_ = plt.hist(trace['std'], bins = 50, label = "std") _ = plt.hist(trace['mean'], bins = 50, label = "mean") _ = plt.legend()Std este centrat în jurul valorii de 1,2, iar media este la 1,55 - destul de aproape!
Să o facem acum de la zero pentru a înțelege Metropolis-Hastings.
De la zero
Generarea unei propuneri
În primul rând, să înțelegem ce face Metropolis-Hastings. Mai devreme în acest articol, am spus: „Metropolis-Hastings selectează aleatoriu mostre diferite dintr-un spațiu”, dar de unde știe care eșantion să selecteze?
Face acest lucru folosind distribuția propunerii. Este o distribuție normală centrată pe eșantionul acceptat în prezent și are un STD de 0,5. Unde 0,5 este un hiperparametru, putem ajusta; cu cât este mai mare BTS a propunerii, cu atât va căuta mai departe din eșantionul acceptat în prezent. Să codificăm asta.
Deoarece trebuie să găsim media și std ale distribuției, această funcție va lua media acceptată în prezent și standardul acceptat în prezent și va returna propuneri pentru ambele.
def get_proposal(mean_current, std_current, proposal_width = 0.5): return np.random.normal(mean_current, proposal_width), \ np.random.normal(std_current, proposal_width)Acceptarea/respingerea unei propuneri
Acum, să codificăm logica care acceptă sau respinge propunerea. Are două părți: anterior și probabilitatea .
Mai întâi, să calculăm probabilitatea ca propunerea să provină din anterior:
def prior(mean, std, prior_mean, prior_std): return st.norm(prior_mean[0], prior_mean[1]).pdf(mean)* \ st.norm(prior_std[0], prior_std[1]).pdf(std)Ia doar media și std și calculează cât de probabil este ca această medie și std să provină din distribuția anterioară pe care am definit-o.
În calcularea probabilității, calculăm cât de probabil este ca datele pe care le-am văzut să provină din distribuția propusă.
def likelihood(mean, std, data): return np.prod(st.norm(mean, std).pdf(X))Deci, pentru fiecare punct de date, înmulțim probabilitatea ca acel punct de date să provină din distribuția propusă.
Acum, trebuie să apelăm aceste funcții pentru media curentă și std și pentru media și std propuse.
prior_current = prior(mean_current, std_current, prior_mean, prior_std) likelihood_current = likelihood(mean_current, std_current, data) prior_proposal = prior(mean_proposal, std_proposal, prior_mean, prior_std) likelihood_proposal = likelihood(mean_proposal, std_proposal, data)Întregul cod:
def accept_proposal(mean_proposal, std_proposal, mean_current, \ std_current, prior_mean, prior_std, data): def prior(mean, std, prior_mean, prior_std): return st.norm(prior_mean[0], prior_mean[1]).pdf(mean)* \ st.norm(prior_std[0], prior_std[1]).pdf(std) def likelihood(mean, std, data): return np.prod(st.norm(mean, std).pdf(X)) prior_current = prior(mean_current, std_current, prior_mean, prior_std) likelihood_current = likelihood(mean_current, std_current, data) prior_proposal = prior(mean_proposal, std_proposal, prior_mean, prior_std) likelihood_proposal = likelihood(mean_proposal, std_proposal, data) return (prior_proposal * likelihood_proposal) / (prior_current * likelihood_current)Acum, să creăm funcția finală care va lega totul și va genera mostrele posterioare de care avem nevoie.
Generarea Posteriorului
Acum, numim funcțiile pe care le-am scris mai sus și generăm posteriorul!
def get_trace(data, samples = 5000): mean_prior = 1 std_prior = 2 mean_current = mean_prior std_current = std_prior trace = { "mean": [mean_current], "std": [std_current] } for i in tqdm(range(samples)): mean_proposal, std_proposal = get_proposal(mean_current, std_current) acceptance_prob = accept_proposal(mean_proposal, std_proposal, mean_current, \ std_current, [mean_prior, std_prior], \ [mean_prior, std_prior], data) if np.random.rand() < acceptance_prob: mean_current = mean_proposal std_current = std_proposal trace['mean'].append(mean_current) trace['std'].append(std_current) return traceLoc pentru imbunatatiri
Log este prietenul tău!
Reamintim a * b = antilog(log(a) + log(b)) și a / b = antilog(log(a) - log(b)).
Acest lucru este benefic pentru noi deoarece vom avea de-a face cu probabilități foarte mici, înmulțind ceea ce va rezulta zero, așa că vom adăuga mai degrabă problema log, problemă rezolvată!
Deci, codul nostru anterior devine:
def accept_proposal(mean_proposal, std_proposal, mean_current, \ std_current, prior_mean, prior_std, data): def prior(mean, std, prior_mean, prior_std): return st.norm(prior_mean[0], prior_mean[1]).logpdf(mean)+ \ st.norm(prior_std[0], prior_std[1]).logpdf(std) def likelihood(mean, std, data): return np.sum(st.norm(mean, std).logpdf(X)) prior_current = prior(mean_current, std_current, prior_mean, prior_std) likelihood_current = likelihood(mean_current, std_current, data) prior_proposal = prior(mean_proposal, std_proposal, prior_mean, prior_std) likelihood_proposal = likelihood(mean_proposal, std_proposal, data) return (prior_proposal + likelihood_proposal) - (prior_current + likelihood_current)Deoarece returnăm jurnalul probabilității de acceptare:
if np.random.rand() < acceptance_prob:
Devine:
if math.log(np.random.rand()) < acceptance_prob:
Să rulăm noul cod și să trasăm rezultatele.
_ = plt.hist(trace['std'], bins = 50, label = "std") _ = plt.hist(trace['mean'], bins = 50, label = "mean") _ = plt.legend()După cum puteți vedea, std este centrat la 1,2, iar media la 1,5. Am reusit!
Inainta
Până acum, sperăm că înțelegi cum funcționează Metropolis-Hastings și s-ar putea să te întrebi unde îl poți folosi.
Ei bine, Bayesian Methods for Hackers este o carte excelentă care explică programarea probabilistică, iar dacă doriți să aflați mai multe despre teorema Bayes și aplicațiile ei, Think Bayes este o carte grozavă a lui Allen B. Downey.
Vă mulțumim pentru citit și sper că acest articol vă încurajează să descoperiți lumea uimitoare a statisticilor bayesiene.
