Makine Öğreniminde Vektör Makine Algoritmasını Destekleyin

Destek Vektör Makine Algoritmaları Hakkında Bilmeniz Gereken Her Şey

Yeni başlayanların çoğu, makine öğrenimi söz konusu olduğunda, doğal olarak regresyon ve sınıflandırma algoritmalarıyla başlar. Bu algoritmalar basit ve takip edilmesi kolaydır. Ancak, makine öğrenmesi kavramlarını daha iyi kavramak için bu iki makine öğrenmesi algoritmasının ötesine geçmek esastır.

Regresyon ve sınıflandırma kadar basit olmasa da çeşitli karmaşık sorunları çözmemize yardımcı olabilecek makine öğreniminde öğrenilecek daha çok şey var. Sizi böyle bir algoritmayla tanıştıralım, Destek Vektör Makinesi Algoritması . Destek Vektör Makinesi algoritması veya SVM algoritması , genellikle hem regresyon hem de sınıflandırma sorunları için verimlilik ve doğruluk sağlayabilen bu tür bir makine öğrenme algoritması olarak adlandırılır.

Makine öğrenimi alanında kariyer yapmayı hayal ediyorsanız, Destek Vektör Makinesi, öğrenim cephanenizin bir parçası olmalıdır. upGrad'da , öğrencilerimizi kariyerlerine başlamak için en iyi makine öğrenimi algoritmalarıyla donatmaya inanıyoruz. İşte makine öğreniminde SVM algoritmasıyla başlamanıza yardımcı olabileceğini düşündüğümüz şeyler .

Destek Vektör Makinesi Algoritması Nedir?

SVM, 2020 yılında oldukça popüler hale gelen ve gelecekte de öyle olmaya devam edecek olan bir tür denetimli öğrenme algoritmasıdır. DVM'nin tarihi 1990 yılına kadar uzanmaktadır; Vapnik'in istatistiksel öğrenme teorisinden alınmıştır. DVM, hem regresyon hem de sınıflandırma zorlukları için kullanılabilir; ancak, çoğunlukla sınıflandırma zorluklarını ele almak için kullanılır.

SVM, N-boyutlu uzayda hiper düzlemler oluşturan ayırt edici bir sınıflandırıcıdır; burada n, gelecekteki veri girdilerini ayırt etmeye yardımcı olmak için bir veri kümesindeki özelliklerin sayısıdır. Kulağa kafa karıştırıcı geliyor, merak etmeyin, basit basit terimlerle anlayacağız.

Destek Vektör Makinesi Algoritması Nasıl Çalışır?

Bir SVM'nin çalışmasını derinlemesine incelemeden önce, bazı temel terminolojileri anlayalım.

hiper düzlem

Bazen karar sınırları veya karar düzlemleri olarak da adlandırılan hiper düzlemler, veri noktalarının sınıflandırılmasına yardımcı olan sınırlardır. Hiper düzlemin yeni bir veri noktasının düştüğü tarafı ayrılabilir veya farklı sınıflara atfedilebilir. Hiper düzlemin boyutu, bir veri kümesine atfedilen özelliklerin sayısına bağlıdır. Veri kümesinin 2 özelliği varsa, hiperdüzlem basit bir çizgi olabilir. Bir veri kümesinin 3 özelliği olduğunda, hiperdüzlem 2 boyutlu bir düzlemdir.

Destek Vektörleri

Destek vektörleri, hiper düzleme en yakın olan ve konumunu etkileyen veri noktalarıdır. Bu vektörler hiper düzlem konumlandırmasını etkilediğinden, destek vektörleri olarak adlandırılırlar ve bu nedenle Destek Vektör Makine Algoritması adını alırlar.

marj

Basitçe söylemek gerekirse, kenar boşluğu, hiperdüzlem ve destek vektörleri arasındaki boşluktur. SVM her zaman marjı maksimize eden hiper düzlemi seçer. Marj ne kadar büyük olursa, sonuçların doğruluğu da o kadar yüksek olur. SVM algoritmalarında kullanılan sert ve yumuşak olmak üzere iki tür kenar boşluğu vardır.

Eğitim veri kümesi doğrusal olarak ayrılabilir olduğunda, SVM marjinal mesafeyi maksimuma çıkaran iki paralel çizgiyi basitçe seçebilir; buna sert marj denir. Eğitim veri kümesi tamamen doğrusal olarak ayrı olmadığında, SVM bazı marj ihlallerine izin verir. Doğruluğun tehlikeye atılmaması için bazı veri noktalarının hiper düzlemin yanlış tarafında veya kenar boşluğu ile hiper düzlem arasında kalmasına izin verir; buna yumuşak kenar boşluğu denir.

Belirli bir veri kümesi için birçok olası hiper düzlem olabilir. VSM'nin amacı, yeni veri noktalarını farklı sınıflara sınıflandırmak için en maksimum marjı seçmektir. Yeni bir veri noktası eklendiğinde, SVM, veri noktasının hiper düzlemin hangi tarafına düştüğünü belirler. SVM, hiper düzlemin yeni veri noktasının düştüğü tarafına bağlı olarak onu farklı sınıflara sınıflandırır.

Okuyun: Makine Öğrenimi için Lineer Cebir: Kritik Kavramlar, Neden Makine Öğrenimi Öncesi Öğrenilir

Destek Vektör Makinalarının Çeşitleri Nelerdir?

Eğitim veri kümesine bağlı olarak, SVM algoritmaları iki tipte olabilir:

Doğrusal DVM

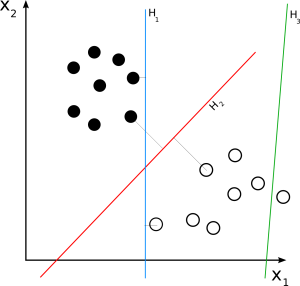
Kaynak

Doğrusal SVM, doğrusal olarak ayrılabilir bir veri kümesi için kullanılır. Basit bir gerçek dünya örneği, doğrusal bir SVM'nin çalışmasını anlamamıza yardımcı olabilir. Tek bir özelliği olan, bir kişinin ağırlığı olan bir veri kümesi düşünün. Veri noktalarının obez veya obez olmayan olmak üzere iki sınıfa ayrıldığı varsayılabilir. Veri noktalarını bu iki sınıfa sınıflandırmak için SVM, en yakın destek vektörlerinin yardımıyla bir maksimal marjlı hiperdüzlem oluşturabilir. Şimdi, ne zaman yeni bir veri noktası eklendiğinde, SVM hiper düzlemin düştüğü tarafını tespit edecek ve kişiyi obez veya obez olarak sınıflandıracaktır.

Doğrusal Olmayan SVM

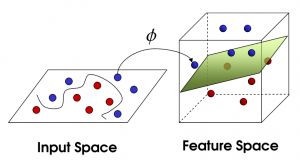
Kaynak

Öznitelik sayısı arttıkça, veri kümesini doğrusal olarak ayırmak zorlaşır. Doğrusal olmayan bir SVM'nin kullanıldığı yer burasıdır. Veri kümesi doğrusal olarak ayrılabilir olmadığında, veri noktalarını ayırmak için düz bir çizgi çizemeyiz. Bu veri noktalarını ayırmak için SVM başka bir boyut ekler. Yeni boyut z, z = x2 + Y2 olarak hesaplanabilir. Bu hesaplama, bir veri kümesinin özelliklerini doğrusal biçimde ayırmaya yardımcı olur ve ardından SVM, veri noktalarını sınıflandırmak için hiper düzlemi oluşturabilir.

Bir veri noktası, yeni bir boyut eklenerek yüksek boyutlu bir uzaya dönüştürüldüğünde, bir hiperdüzlem ile kolayca ayrılabilir hale gelir. Bu, çekirdek hilesi denilen şeyin yardımıyla yapılır. Çekirdek hilesi ile SVM algoritmaları , ayrılamayan verileri ayrılabilir verilere dönüştürebilir.

Çekirdek nedir?

Çekirdek, düşük boyutlu girdileri alan ve bunları yüksek boyutlu uzaya dönüştüren bir fonksiyondur. Ayrıca, SVM çıktılarının doğruluğunu artırmaya yardımcı olan bir ayar parametresi olarak da adlandırılır. Ayrılamayan veri kümesini ayrılabilir bir veri kümesine dönüştürmek için bazı karmaşık veri dönüşümleri gerçekleştirirler.

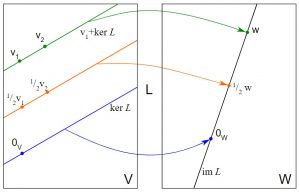
Kaynak

SVM Çekirdeklerinin Farklı Türleri Nelerdir?

Doğrusal Çekirdek

Adından da anlaşılacağı gibi, doğrusal çekirdek, doğrusal olarak ayrılabilir veri kümeleri için kullanılır. Çoğunlukla çok sayıda özelliğe sahip veri kümeleri, örneğin tüm alfabelerin yeni bir özellik olduğu metin sınıflandırması için kullanılır. Doğrusal çekirdeğin sözdizimi şöyledir:

K(x, y) = toplam(x*y)

sözdizimindeki x ve y iki vektördür.

Bir SVM'yi doğrusal bir çekirdekle eğitmek, onu diğer herhangi bir çekirdekle eğitmekten daha hızlıdır, çünkü gama parametresinin değil, yalnızca C düzenlileştirme parametresinin optimizasyonunu gerektirir.

polinom çekirdeği

Polinom çekirdeği, doğrusal olmayan veri kümesinin dönüştürülmesinde yararlı olan doğrusal çekirdeğin daha genelleştirilmiş bir biçimidir. Polinom çekirdeğin formülü aşağıdaki gibidir:

K(x, y) = (xT*y + c)d

Burada x ve y iki vektördür, c, daha yüksek ve daha düşük boyut terimleri için değiş tokuşa izin veren bir sabittir ve d, çekirdeğin sırasıdır. Geliştiricinin, algoritmada çekirdeğin sırasına manuel olarak karar vermesi gerekiyor.

Radyal Temel Fonksiyon Çekirdeği

Gauss çekirdeği olarak da adlandırılan radyal tabanlı fonksiyon çekirdeği, sınıflandırma problemlerini çözmek için SVM algoritmalarında yaygın olarak kullanılan bir çekirdektir . Girdi verilerini belirsiz yüksek boyutlu uzaylara eşleme potansiyeline sahiptir. Radyal tabanlı fonksiyon çekirdeği matematiksel olarak şu şekilde temsil edilebilir:

K(x, y) = exp(-gamma*sum(x – y2))

Burada x ve y iki vektördür ve gama 0 ile 1 arasında değişen bir ayar parametresidir. Gama, öğrenme algoritmasında manuel olarak önceden tanımlanmıştır.

Doğrusal, polinom ve radyal temel işlevleri, hiperdüzlem oluşturma kararları ve doğruluğu sağlamak için matematiksel yaklaşımlarında farklılık gösterir. Doğrusal ve polinom çekirdekler eğitimde daha az zaman harcar ancak daha az doğruluk sağlar. Öte yandan, radyal tabanlı fonksiyon çekirdeği, eğitimde daha fazla zaman alır ancak sonuçlar açısından daha yüksek doğruluk sağlar.

Şimdi ortaya çıkan soru, veri kümeniz için hangi çekirdeğin kullanılacağını nasıl seçeceğinizdir. Kararınız yalnızca veri kümesinin karmaşıklığına ve istediğiniz sonuçların doğruluğuna bağlı olmalıdır. Elbette herkes yüksek doğrulukta sonuçlar ister, ancak bu aynı zamanda çözümü geliştirmek için ne kadar zamanınız olduğuna ve bunun için ne kadar harcayabileceğinize de bağlıdır. Ayrıca, radyal tabanlı fonksiyon çekirdeği genellikle daha yüksek doğruluk sağlar, ancak bazı durumlarda doğrusal ve polinom çekirdekleri eşit derecede iyi performans gösterebilir.

Örneğin, doğrusal olarak ayrılabilir veriler için, doğrusal bir çekirdek, radyal tabanlı bir çekirdek kadar iyi performans gösterecek ve daha az eğitim süresi tüketecektir. Dolayısıyla, veri kümeniz doğrusal olarak ayrılabilir ise, doğrusal bir çekirdek seçmelisiniz. Doğrusal olmayan veriler için, sahip olduğunuz zaman ve harcamaya bağlı olarak polinom veya radyal tabanlı bir fonksiyon seçmelisiniz.

Çekirdeklerde Kullanılan Ayar Parametreleri Nelerdir?

C düzenlileştirme

C düzenlileştirme parametresi, her eğitim veri kümesinde belirli bir düzeyde yanlış sınıflandırmaya izin vermek için sizden değerleri kabul eder. Daha yüksek C düzenlileştirme değerleri, küçük marjlı hiperdüzleme yol açar ve fazla yanlış sınıflandırmaya izin vermez. Daha düşük değerler ise yüksek marj ve daha fazla yanlış sınıflandırmaya yol açar.

Gama

Gama parametresi, hiper düzlemin konumunu etkileyecek destek vektörlerinin aralığını tanımlar. Yüksek gama değeri yalnızca yakındaki veri noktalarını, düşük değer ise uzaktaki noktaları dikkate alır.

Python'da Destek Vektör Makinesi Algoritması Nasıl Uygulanır?

Kaynak

SVM algoritmasının ne olduğu ve nasıl çalıştığı hakkında temel bir fikre sahip olduğumuza göre, daha karmaşık bir şeye geçelim. Şimdi Python'da SVM algoritmasını uygulamak ve çalıştırmak için genel adımlara bakacağız . SVM algoritmasının nasıl uygulanacağını öğrenmek için Python'un Scikit-Learn kitaplığını kullanacağız .

Her şeyden önce, SVM algoritmalarını çalıştırmak için gerekli olan Pandas ve NumPy gibi tüm gerekli kitaplıkları içe aktarmalıyız . Tüm kütüphaneleri yerleştirdikten sonra, eğitim veri setini içe aktarmalıyız. Ardından, veri setimizi analiz etmeliyiz. Bir veri kümesini analiz etmenin birden çok yolu vardır.

Örneğin, verilerin boyutlarını kontrol edebilir, yanıt ve açıklayıcı değişkenlere bölebilir ve veri setimizi analiz etmek için KPI'lar ayarlayabiliriz. Veri analizini tamamladıktan sonra, veri setini önceden işlememiz gerekir. Veri setimizde alakasız, eksik ve yanlış veri olup olmadığını kontrol etmeliyiz.

Şimdi eğitim kısmı geliyor. Algoritmamızı ilgili kernel ile kodlamalı ve eğitmeliyiz. Scikit-Learn, eğitim algoritmaları için bazı yerleşik sınıfları bulabileceğiniz SVM kitaplığını içerir. SVM kitaplığı, algoritmalarınızı eğitmek için kullanmak istediğiniz çekirdek türünün değerini kabul eden bir SVC sınıfı içerir.

Ardından, algoritmanızı eğiten SVC sınıfının fit yöntemine parametre olarak eklenen fit yöntemini çağırırsınız. Daha sonra algoritma için tahminler yapmak için SVC sınıfının tahmin yöntemini kullanmanız gerekir. Tahmin adımını tamamladıktan sonra, algoritmanızı değerlendirmek ve sonucu görmek için metrik kitaplığının sınıflandırma_raporunu ve karışıklık_matrix'ini çağırmanız gerekir.

Destek Vektör Makinesi algoritmasının uygulamaları nelerdir?

SVM algoritmaları , çeşitli regresyon ve sınıflandırma zorluklarını kapsayan uygulamalara sahiptir. SVM algoritmalarının temel uygulamalarından bazıları şunlardır:

• Metin ve köprü metni sınıflandırması
• Görüntü sınıflandırması
• Sentetik Açıklıklı Radar (SAR) gibi uydu verilerinin sınıflandırılması
• Proteinler gibi biyolojik maddelerin sınıflandırılması
• El yazısı metinde karakter tanıma

Destek Vektör Makinesi Algoritmasını Neden Kullanmalı?

SVM algoritması aşağıdakiler gibi çeşitli avantajlar sunar:

• Doğrusal olmayan verileri ayırmada etkilidir
• Hem düşük hem de yüksek boyutlu alanlarda son derece hassas
• Destek vektörleri yalnızca hiper düzlemin konumunu etkilediğinden, aşırı uyum sorununa karşı bağışıklık kazanın.

Bakın : Sinir Ağlarında Bilmeniz Gereken 6 Tip Aktivasyon Fonksiyonu

Özetliyor

Destek Vektör Makine Algoritmasını bu yazımızda detaylı olarak inceledik . SVM algoritmasını , nasıl çalıştığını, türlerini, uygulamalarını, faydalarını ve Python'daki uygulamasını öğrendik . Bu makale size SVM algoritması hakkında temel bir fikir verecek ve bazı sorularınızı yanıtlayacaktır.

Ancak, SVM algoritmasının doğru hiper düzlemin hangisi olduğunu nasıl bildiği, Python'da mevcut olan diğer kütüphaneler ve eğitim veri setinin nerede bulunacağı gibi başka soruları da beraberinde getirecektir. Makine öğrenimi hakkında daha fazla bilgi edinmek istiyorsanız, çalışan profesyoneller için tasarlanmış ve 450+ saat zorlu eğitim, 30'dan fazla vaka çalışması ve ödev, IIIT- sunan IIIT-B & upGrad'ın Makine Öğrenimi ve Yapay Zeka PG Diplomasına göz atın. B Mezun statüsü, 5'ten fazla pratik uygulamalı bitirme projesi ve en iyi firmalarla iş yardımı.