Algoritmo de máquina de vectores de soporte en aprendizaje automático

Todo lo que necesita saber sobre los algoritmos de máquinas de vectores de soporte

La mayoría de los principiantes, cuando se trata de aprendizaje automático, comienzan naturalmente con algoritmos de regresión y clasificación . Estos algoritmos son simples y fáciles de seguir. Sin embargo, es esencial ir más allá de estos dos algoritmos de aprendizaje automático para comprender mejor los conceptos de aprendizaje automático.

Hay mucho más que aprender en el aprendizaje automático, que puede no ser tan simple como la regresión y la clasificación, pero puede ayudarnos a resolver varios problemas complejos. Permítanos presentarle uno de esos algoritmos, el algoritmo de máquina de vectores de soporte . El algoritmo Support Vector Machine , o algoritmo SVM , generalmente se conoce como uno de esos algoritmos de aprendizaje automático que puede brindar eficiencia y precisión tanto para problemas de regresión como de clasificación.

Si sueña con seguir una carrera en el campo del aprendizaje automático, entonces Support Vector Machine debería ser parte de su arsenal de aprendizaje. En upGrad , creemos en equipar a nuestros estudiantes con los mejores algoritmos de aprendizaje automático para comenzar sus carreras. Esto es lo que creemos que puede ayudarlo a comenzar con el algoritmo SVM en el aprendizaje automático.

¿Qué es un algoritmo de máquina de vectores de soporte?

SVM es un tipo de algoritmo de aprendizaje supervisado que se ha vuelto muy popular en 2020 y lo seguirá siendo en el futuro. La historia de SVM se remonta a 1990; se extrae de la teoría del aprendizaje estadístico de Vapnik. SVM se puede utilizar tanto para desafíos de regresión como de clasificación; sin embargo, se usa principalmente para abordar los desafíos de clasificación.

SVM es un clasificador discriminativo que crea hiperplanos en un espacio N-dimensional, donde n es el número de características en un conjunto de datos para ayudar a discriminar futuras entradas de datos. Suena confuso, no te preocupes, lo entenderemos en términos sencillos.

¿Cómo funciona un algoritmo de máquina de vectores de soporte?

Antes de profundizar en el funcionamiento de una SVM, comprendamos algunas de las terminologías clave.

Hiperplano

Los hiperplanos, que a veces también se denominan límites de decisión o planos de decisión, son los límites que ayudan a clasificar los puntos de datos. El lado del hiperplano, donde cae un nuevo punto de datos, se puede segregar o atribuir a diferentes clases. La dimensión del hiperplano depende de la cantidad de características que se atribuyen a un conjunto de datos. Si el conjunto de datos tiene 2 características, entonces el hiperplano puede ser una línea simple. Cuando un conjunto de datos tiene 3 características, entonces el hiperplano es un plano bidimensional.

Vectores de apoyo

Los vectores de soporte son los puntos de datos que están más cerca del hiperplano y afectan su posición. Dado que estos vectores afectan el posicionamiento del hiperplano, se denominan vectores de soporte y, por lo tanto, el nombre Algoritmo de máquina de vectores de soporte.

Margen

En pocas palabras, el margen es la brecha entre el hiperplano y los vectores de soporte. SVM siempre elige el hiperplano que maximiza el margen. Cuanto mayor sea el margen, mayor será la precisión de los resultados. Hay dos tipos de márgenes que se utilizan en los algoritmos SVM , rígidos y blandos.

Cuando el conjunto de datos de entrenamiento es linealmente separable, SVM puede simplemente seleccionar dos líneas paralelas que maximicen la distancia marginal; esto se llama un margen duro. Cuando el conjunto de datos de entrenamiento no está completamente separado linealmente, SVM permite alguna violación de margen. Permite que algunos puntos de datos permanezcan en el lado equivocado del hiperplano o entre el margen y el hiperplano para que la precisión no se vea comprometida; esto se llama un margen blando.

Puede haber muchos hiperplanos posibles para un conjunto de datos dado. El objetivo de VSM es seleccionar el margen más máximo para clasificar nuevos puntos de datos en diferentes clases. Cuando se agrega un nuevo punto de datos, la SVM determina de qué lado del hiperplano cae el punto de datos. Según el lado del hiperplano donde cae el nuevo punto de datos, SVM lo clasifica en diferentes clases.

Lea: Álgebra lineal para el aprendizaje automático: conceptos críticos, por qué aprender antes de ML

¿Cuáles son los tipos de máquinas de vectores de soporte?

Según el conjunto de datos de entrenamiento, los algoritmos SVM pueden ser de dos tipos:

MVS lineal

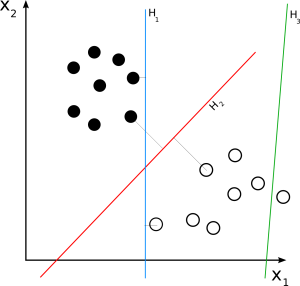
Fuente

SVM lineal se utiliza para un conjunto de datos linealmente separable. Un ejemplo simple del mundo real puede ayudarnos a comprender el funcionamiento de una SVM lineal. Considere un conjunto de datos que tiene una sola característica, el peso de una persona. Se supone que los puntos de datos se clasifican en dos clases, obesos o no obesos. Para clasificar los puntos de datos en estas dos clases, SVM puede crear un hiperplano de margen máximo con la ayuda de los vectores de soporte más cercanos. Ahora, cada vez que se agregue un nuevo punto de datos, el SVM detectará el lado del hiperplano, dónde cae, y clasificará a la persona como obesa o no.

SVM no lineal

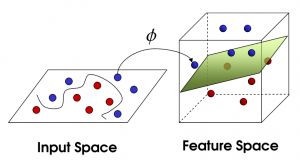
Fuente

A medida que aumenta la cantidad de características, separar el conjunto de datos linealmente se vuelve un desafío. Ahí es donde se usa una SVM no lineal. No podemos dibujar una línea recta para separar puntos de datos cuando el conjunto de datos no es linealmente separable. Entonces, para separar estos puntos de datos, SVM agrega otra dimensión. La nueva dimensión z se puede calcular como z = x2 + Y2. Este cálculo ayudará a separar las características de un conjunto de datos en forma lineal, y luego SVM puede crear el hiperplano para clasificar los puntos de datos.

Cuando un punto de datos se transforma en un espacio de gran dimensión al agregar una nueva dimensión, se vuelve fácilmente separable con un hiperplano. Esto se hace con la ayuda de lo que se llama el truco del núcleo. Con el truco del núcleo, los algoritmos SVM pueden transformar datos no separables en datos separables.

¿Qué es un núcleo?

Un kernel es una función que toma entradas de baja dimensión y las transforma en espacio de alta dimensión. También se lo conoce como un parámetro de ajuste que ayuda a aumentar la precisión de las salidas de SVM. Realizan algunas transformaciones de datos complejas para convertir el conjunto de datos no separable en uno separable.

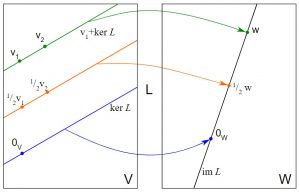
Fuente

¿Cuáles son los diferentes tipos de kernels SVM?

Núcleo lineal

Como sugiere el nombre, el núcleo lineal se usa para conjuntos de datos linealmente separables. Se utiliza principalmente para conjuntos de datos con una gran cantidad de características, clasificación de texto, por ejemplo, donde todos los alfabetos son una característica nueva. La sintaxis del kernel lineal es:

K(x, y) = suma(x*y)

x e y en la sintaxis son dos vectores.

Entrenar una SVM con un kernel lineal es más rápido que entrenarla con cualquier otro kernel, ya que requiere la optimización solo del parámetro de regularización C y no del parámetro gamma.

Núcleo polinomial

El kernel polinomial es una forma más generalizada del kernel lineal que es útil para transformar conjuntos de datos no lineales. La fórmula del núcleo polinomial es la siguiente:

K(x, y) = (xT*y + c)d

Aquí x e y son dos vectores, c es una constante que permite el intercambio de términos de dimensión superior e inferior, y d es el orden del núcleo. Se supone que el desarrollador debe decidir el orden del núcleo manualmente en el algoritmo.

Núcleo de función de base radial

El kernel de función de base radial, también conocido como kernel gaussiano, es un kernel ampliamente utilizado en los algoritmos SVM para resolver problemas de clasificación. Tiene el potencial de mapear datos de entrada en espacios indefinidos de alta dimensión. El núcleo de la función de base radial se puede representar matemáticamente como:

K(x, y) = exp(-gamma*suma(x – y2))

Aquí, x e y son dos vectores, y gamma es un parámetro de ajuste que va de 0 a 1. Gamma está predefinido manualmente en el algoritmo de aprendizaje.

Las funciones de base lineal, polinómica y radial difieren en su enfoque matemático para tomar las decisiones y la precisión de la creación del hiperplano. Los núcleos lineales y polinómicos consumen menos tiempo de entrenamiento pero brindan menos precisión. Por otro lado, el núcleo de la función de base radial requiere más tiempo de entrenamiento pero proporciona una mayor precisión en términos de resultados.

Ahora, la pregunta que surge es cómo elegir qué kernel usar para su conjunto de datos. Su decisión debe depender únicamente de la complejidad del conjunto de datos y la precisión de los resultados que desea. Por supuesto, todos quieren resultados de alta precisión, pero también depende del tiempo que tenga para desarrollar la solución y cuánto pueda gastar en ella. Además, el núcleo de la función de base radial generalmente proporciona una mayor precisión, pero en algunas circunstancias, los núcleos lineales y polinómicos pueden funcionar igualmente bien.

Por ejemplo, para datos linealmente separables, un kernel lineal funcionará tan bien como un kernel de base radial y consumirá menos tiempo de entrenamiento. Entonces, si su conjunto de datos es linealmente separable, debe elegir un núcleo lineal. Para datos no lineales, debe elegir una función de base polinomial o radial según el tiempo y los gastos que tenga.

¿Cuáles son los parámetros de ajuste utilizados con los núcleos?

C regularización

El parámetro de regularización C acepta valores de usted para permitir un cierto nivel de clasificación errónea en cada conjunto de datos de entrenamiento. Los valores de regularización de C más altos conducen a un hiperplano de margen pequeño y no permiten muchos errores de clasificación. Los valores más bajos, por otro lado, conducen a un alto margen y una mayor clasificación errónea.

Gama

El parámetro gamma define el rango de vectores de soporte que afectarán el posicionamiento del hiperplano. El valor gamma alto considera solo los puntos de datos cercanos y el valor bajo considera los puntos lejanos.

¿Cómo implementar el algoritmo de máquina de vectores de soporte en Python?

Fuente

Ya que tenemos la idea básica de qué es el algoritmo SVM y cómo funciona, profundicemos en algo más complejo. Ahora veremos los pasos generales para implementar y ejecutar el algoritmo SVM en Python. Usaremos la biblioteca Scikit-Learn de Python para aprender a implementar el algoritmo SVM.

En primer lugar, tenemos que importar todas las bibliotecas necesarias, como Pandas y NumPy, que son necesarias para ejecutar los algoritmos SVM. Una vez que tengamos todas las bibliotecas en el lugar, debemos importar el conjunto de datos de entrenamiento. A continuación, tenemos que analizar nuestro conjunto de datos. Hay varias formas de analizar un conjunto de datos.

Por ejemplo, podemos verificar las dimensiones de los datos, dividirlos en variables de respuesta y explicativas, y establecer KPI para analizar nuestro conjunto de datos. Después de completar el análisis de datos, tenemos que preprocesar el conjunto de datos. Debemos buscar datos irrelevantes, incompletos e incorrectos en nuestro conjunto de datos.

Ahora viene la parte del entrenamiento. Tenemos que codificar y entrenar nuestro algoritmo con el kernel relevante. Scikit-Learn contiene la biblioteca SVM, donde puede encontrar algunas clases integradas para entrenar algoritmos. La biblioteca SVM contiene una clase SVC que acepta el valor del tipo de kernel que desea usar para entrenar sus algoritmos.

Luego llama al método de ajuste de la clase SVC que entrena su algoritmo, insertado como parámetro para el método de ajuste. Luego, debe usar el método de predicción de la clase SVC para hacer predicciones para el algoritmo. Una vez que haya completado el paso de predicción, debe llamar a la clasificación_report y confusion_matrix de la biblioteca de métricas para evaluar su algoritmo y ver el resultado.

¿Cuáles son las aplicaciones del algoritmo de la máquina de vectores de soporte?

Los algoritmos SVM tienen aplicaciones en varios desafíos de regresión y clasificación. Algunas de las aplicaciones clave de los algoritmos SVM son:

• Clasificación de texto e hipertexto
• Clasificación de imágenes
• Clasificación de datos satelitales como el radar de apertura sintética (SAR)
• Clasificación de sustancias biológicas como las proteínas.
• Reconocimiento de caracteres en texto escrito a mano

¿Por qué utilizar el algoritmo de máquina de vectores de soporte?

El algoritmo SVM ofrece varios beneficios, tales como:

• Eficaz en la separación de datos no lineales
• Alta precisión en espacios dimensionales inferiores y superiores
• Inmune al problema de sobreajuste ya que los vectores de apoyo solo afectan la posición del hiperplano.

Consulte: 6 tipos de funciones de activación en redes neuronales que debe conocer

Resumiendo

Hemos analizado en detalle el algoritmo de la máquina de vectores de soporte en este artículo. Aprendimos sobre el algoritmo SVM , cómo funciona, sus tipos, aplicaciones, beneficios e implementación en Python. Este artículo le dará una idea básica sobre el algoritmo SVM y responderá algunas de sus preguntas.

Pero también traerá algunas otras preguntas, como cómo el algoritmo SVM sabe cuál es el hiperplano correcto, qué otras bibliotecas están disponibles en Python y dónde encontrar el conjunto de datos de entrenamiento. Si está interesado en obtener más información sobre el aprendizaje automático, consulte el Diploma PG en aprendizaje automático e inteligencia artificial de IIIT-B y upGrad, que está diseñado para profesionales que trabajan y ofrece más de 450 horas de capacitación rigurosa, más de 30 estudios de casos y asignaciones, IIIT- B Estado de exalumno, más de 5 proyectos prácticos finales prácticos y asistencia laboral con las mejores empresas.