Obsługa algorytmu maszyny wektorowej w uczeniu maszynowym

Wszystko, co musisz wiedzieć o algorytmach maszyn wektorów nośnych

Większość początkujących, jeśli chodzi o uczenie maszynowe, naturalnie zaczyna od algorytmów regresji i klasyfikacji . Te algorytmy są proste i łatwe do naśladowania. Jednak konieczne jest wyjście poza te dwa algorytmy uczenia maszynowego, aby lepiej zrozumieć koncepcje uczenia maszynowego.

W uczeniu maszynowym jest dużo więcej do nauczenia, które może nie być tak proste jak regresja i klasyfikacja, ale może pomóc nam rozwiązać różne złożone problemy. Pozwól, że przedstawimy Ci jeden z takich algorytmów, algorytm maszyny wektorów nośnych . Algorytm maszyny wektorów wsparcia lub algorytm SVM jest zwykle określany jako jeden z takich algorytmów uczenia maszynowego, który może zapewnić wydajność i dokładność zarówno w przypadku problemów z regresją, jak i klasyfikacją.

Jeśli marzysz o karierze w dziedzinie uczenia maszynowego, maszyna wektorów wsparcia powinna być częścią twojego arsenału uczenia się. W upGrad wierzymy, że wyposażymy naszych uczniów w najlepsze algorytmy uczenia maszynowego, aby rozpocząć karierę. Oto, co naszym zdaniem może pomóc Ci rozpocząć pracę z algorytmem SVM w uczeniu maszynowym.

Co to jest algorytm maszyny wektora nośnego?

SVM to rodzaj nadzorowanego algorytmu uczenia się, który stał się bardzo popularny w 2020 r. i będzie taki w przyszłości. Historia SVM sięga 1990 roku; wywodzi się z statystycznej teorii uczenia się Vapnika. SVM może być używany zarówno do wyzwań regresji, jak i klasyfikacji; jednak jest używany głównie do rozwiązywania problemów związanych z klasyfikacją.

SVM to klasyfikator dyskryminacyjny, który tworzy hiperpłaszczyzny w przestrzeni N-wymiarowej, gdzie n jest liczbą funkcji w zbiorze danych, aby pomóc w rozróżnianiu przyszłych danych wejściowych. Brzmi niejasno, nie martw się, zrozumiemy to w prosty sposób.

Jak działa algorytm maszyny wektora nośnego?

Zanim zagłębimy się w działanie maszyny SVM, zapoznajmy się z niektórymi kluczowymi terminologiami.

Hyperplane

Hiperpłaszczyzny, które są czasami nazywane granicami decyzyjnymi lub płaszczyznami decyzyjnymi, to granice ułatwiające klasyfikację punktów danych. Strona hiperpłaszczyzny, na której znajduje się nowy punkt danych, może być oddzielona lub przypisana do różnych klas. Wymiar hiperpłaszczyzny zależy od liczby cech przypisanych do zestawu danych. Jeśli zbiór danych ma 2 cechy, hiperpłaszczyzna może być prostą linią. Gdy zestaw danych ma 3 funkcje, hiperpłaszczyzna jest płaszczyzną dwuwymiarową.

Wektory wsparcia

Wektory nośne to punkty danych, które znajdują się najbliżej hiperpłaszczyzny i wpływają na jej położenie. Ponieważ te wektory wpływają na pozycjonowanie hiperpłaszczyzny, są one określane jako wektory nośne i stąd nazwa Algorytm maszyny wektorów nośnych.

Margines

Mówiąc prościej, margines jest przerwą między hiperpłaszczyzną a wektorami nośnymi. SVM zawsze wybiera hiperpłaszczyznę, która maksymalizuje margines. Im większa marża, tym wyższa dokładność wyników. Istnieją dwa rodzaje marginesów, które są używane w algorytmach SVM , twardy i miękki.

Gdy zestaw danych uczących można liniowo oddzielić, SVM może po prostu wybrać dwie równoległe linie, które maksymalizują odległość marginalną; nazywa się to twardym marginesem. Gdy treningowy zestaw danych nie jest w pełni liniowo oddzielony, SVM pozwala na pewne naruszenie marginesu. Pozwala to niektórym punktom danych pozostać po niewłaściwej stronie hiperpłaszczyzny lub między marginesem a hiperpłaszczyzną, dzięki czemu dokładność nie jest zagrożona; nazywa się to miękkim marginesem.

Dla danego zbioru danych może istnieć wiele możliwych hiperpłaszczyzn. Celem VSM jest wybranie jak największego marginesu do zaklasyfikowania nowych punktów danych do różnych klas. Po dodaniu nowego punktu danych SVM określa, po której stronie hiperpłaszczyzny wypada punkt danych. W oparciu o stronę hiperpłaszczyzny, na której znajduje się nowy punkt danych, SVM klasyfikuje go następnie na różne klasy.

Przeczytaj: Algebra liniowa do uczenia maszynowego: krytyczne pojęcia, po co uczyć się przed ML

Jakie są typy maszyn wektorów nośnych?

Na podstawie uczącego zbioru danych algorytmy SVM mogą być dwojakiego rodzaju:

Liniowa SVM

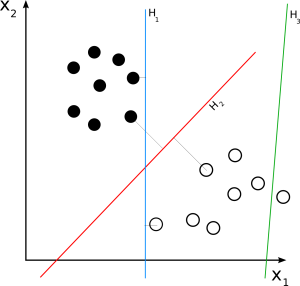
Źródło

Linear SVM jest używany do liniowo separowanego zestawu danych. Prosty przykład ze świata rzeczywistego może pomóc nam zrozumieć działanie liniowej maszyny SVM. Rozważmy zbiór danych, który ma jedną cechę, wagę osoby. Punkty danych można podzielić na dwie klasy, otyłe lub nieotyłe. Aby zaklasyfikować punkty danych do tych dwóch klas, SVM może utworzyć hiperpłaszczyznę z maksymalnym marginesem za pomocą najbliższych wektorów wsparcia. Teraz, za każdym razem, gdy dodawany jest nowy punkt danych, SVM wykryje stronę hiperpłaszczyzny, gdzie spada, i zaklasyfikuje osobę jako otyłą lub nie.

Nieliniowa SVM

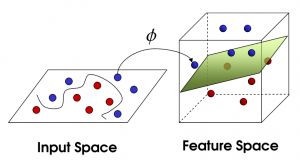
Źródło

Wraz ze wzrostem liczby funkcji liniowa separacja zestawu danych staje się wyzwaniem. W tym przypadku używana jest nieliniowa maszyna SVM. Nie możemy narysować linii prostej do oddzielenia punktów danych, gdy zbiór danych nie jest liniowo oddzielony. Aby oddzielić te punkty danych, SVM dodaje kolejny wymiar. Nowy wymiar z można obliczyć jako z = x2 + Y2. To obliczenie pomoże oddzielić cechy zestawu danych w formie liniowej, a następnie SVM może utworzyć hiperpłaszczyznę do klasyfikowania punktów danych.

Kiedy punkt danych jest przekształcany w przestrzeń o dużych wymiarach poprzez dodanie nowego wymiaru, łatwo można go oddzielić za pomocą hiperpłaszczyzny. Odbywa się to za pomocą tak zwanej sztuczki jądra. Dzięki sztuczce jądra algorytmy SVM mogą przekształcać dane nierozdzielne w dane dające się oddzielić.

Co to jest jądro?

Jądro to funkcja, która pobiera dane wejściowe o małych wymiarach i przekształca je w przestrzeń o dużych wymiarach. Jest również określany jako parametr strojenia, który pomaga zwiększyć dokładność wyjść SVM. Wykonują złożone transformacje danych w celu przekształcenia nierozdzielnego zestawu danych w dający się oddzielić.

Źródło

Jakie są różne typy jąder SVM?

Jądro liniowe

Jak sama nazwa wskazuje, jądro liniowe jest używane do liniowo separowalnych zbiorów danych. Jest używany głównie w przypadku zestawów danych z dużą liczbą funkcji, na przykład klasyfikacją tekstu, gdzie wszystkie alfabety są nową funkcją. Składnia jądra liniowego to:

K(x, y) = suma(x*y)

x i y w składni to dwa wektory.

Trenowanie SVM z jądrem liniowym jest szybsze niż trenowanie z dowolnym innym jądrem, ponieważ wymaga optymalizacji tylko parametru regularyzacji C, a nie parametru gamma.

Jądro wielomianowe

Jądro wielomianowe jest bardziej uogólnioną formą jądra liniowego, która jest przydatna w przekształcaniu nieliniowego zbioru danych. Wzór jądra wielomianowego jest następujący:

K(x, y) = (xT*y + c)d

Tutaj x i y są dwoma wektorami, c jest stałą, która pozwala na kompromis między wyższymi i niższymi warunkami wymiaru, a d jest porządkiem jądra. Deweloper ma ręcznie określić kolejność jądra w algorytmie.

Jądro funkcji promieniowej podstawy

Jądro funkcji radialnej, zwane również jądrem Gaussa, jest szeroko stosowanym jądrem w algorytmach SVM do rozwiązywania problemów klasyfikacyjnych. Ma potencjał do mapowania danych wejściowych w nieokreślone, wielowymiarowe przestrzenie. Jądro radialnej funkcji bazowej można przedstawić matematycznie jako:

K(x, y) = exp(-gamma*sum(x – y2))

Tutaj x i y są dwoma wektorami, a gamma jest parametrem strojenia z zakresu od 0 do 1. Gamma jest wstępnie definiowana ręcznie w algorytmie uczenia.

Liniowe, wielomianowe i radialne funkcje bazowe różnią się pod względem matematycznego podejścia do podejmowania decyzji i dokładności tworzenia hiperpłaszczyzn. Jądra liniowe i wielomianowe zajmują mniej czasu podczas uczenia, ale zapewniają mniejszą dokładność. Z drugiej strony, uczenie jądra radialnej funkcji bazowej zajmuje więcej czasu, ale zapewnia większą dokładność wyników.

Teraz pojawia się pytanie, jak wybrać jądro, które ma być używane w zestawie danych. Twoja decyzja powinna zależeć wyłącznie od złożoności zbioru danych i dokładności żądanych wyników. Oczywiście każdy chce wyników o wysokiej dokładności, ale zależy to również od czasu, jaki masz na opracowanie rozwiązania i ile możesz na to wydać. Ponadto jądro funkcji radialnej zapewnia większą dokładność, ale w pewnych okolicznościach jądra liniowe i wielomianowe mogą działać równie dobrze.

Na przykład, w przypadku danych liniowo separowanych, jądro liniowe będzie działać tak samo jak jądro radialne i zużywając mniej czasu na szkolenie. Więc jeśli twój zbiór danych daje się oddzielić liniowo, powinieneś wybrać jądro liniowe. W przypadku danych nieliniowych należy wybrać wielomianową lub radialną funkcję bazową w zależności od posiadanego czasu i wydatków.

Jakie są parametry dostrajania używane z jądrami?

Regulacja C

Parametr regularyzacji C przyjmuje wartości od Ciebie, aby umożliwić pewien poziom błędnej klasyfikacji w każdym uczącym zbiorze danych. Wyższe wartości regularyzacji C prowadzą do hiperpłaszczyzny o małym marginesie i nie pozwalają na dużą błędną klasyfikację. Z drugiej strony niższe wartości prowadzą do wysokiej marży i większej błędnej klasyfikacji.

Gamma

Parametr gamma określa zakres wektorów wsparcia, które będą miały wpływ na położenie hiperpłaszczyzny. Wysoka wartość gamma uwzględnia tylko pobliskie punkty danych, a niska wartość uwzględnia odległe punkty.

Jak zaimplementować algorytm maszyny wektora wsparcia w Pythonie?

Źródło

Ponieważ mamy podstawowe pojęcie o tym, czym jest algorytm SVM i jak działa, zagłębimy się w coś bardziej złożonego. Teraz przyjrzymy się ogólnym krokom implementacji i uruchomienia algorytmu SVM w Pythonie. Będziemy używać biblioteki Scikit-Learn języka Python, aby nauczyć się implementować algorytm SVM.

Przede wszystkim musimy zaimportować wszystkie niezbędne biblioteki, takie jak Pandas i NumPy, które są niezbędne do uruchomienia algorytmów SVM. Gdy mamy już wszystkie biblioteki na miejscu, musimy zaimportować zestaw danych uczących. Następnie musimy przeanalizować nasz zbiór danych. Istnieje wiele sposobów analizy zbioru danych.

Na przykład możemy sprawdzić wymiary danych, podzielić je na zmienne odpowiedzi i objaśniające oraz ustawić KPI do analizy naszego zbioru danych. Po zakończeniu analizy danych musimy wstępnie przetworzyć zbiór danych. Powinniśmy sprawdzić, czy w naszym zbiorze danych nie ma nieistotnych, niekompletnych i nieprawidłowych danych.

Teraz nadchodzi część szkoleniowa. Musimy zakodować i wytrenować nasz algorytm z odpowiednim jądrem. Scikit-Learn zawiera bibliotekę SVM, w której można znaleźć kilka wbudowanych klas do uczenia algorytmów. Biblioteka SVM zawiera klasę SVC, która akceptuje wartość typu jądra, którego chcesz użyć do trenowania algorytmów.

Następnie wywołujesz metodę fit klasy SVC, która uczy twój algorytm, wstawianą jako parametr do metody fit. Następnie musisz użyć metody przewidywania klasy SVC, aby dokonać przewidywań dla algorytmu. Po zakończeniu etapu przewidywania musisz wywołać klasyfikacje_raport i macierz_pomyłek biblioteki metryk, aby ocenić algorytm i zobaczyć wynik.

Jakie są zastosowania algorytmu maszyny wektorów nośnych?

Algorytmy SVM mają zastosowanie w różnych wyzwaniach regresji i klasyfikacji. Niektóre z kluczowych zastosowań algorytmów SVM to:

• Klasyfikacja tekstu i hipertekstu
• Klasyfikacja obrazu
• Klasyfikacja danych satelitarnych, takich jak radar z syntetyczną aperturą (SAR)
• Klasyfikacja substancji biologicznych, takich jak białka
• Rozpoznawanie znaków w tekście pisanym odręcznie

Dlaczego warto korzystać z algorytmu maszyny wektorów nośnych?

Algorytm SVM oferuje różne korzyści, takie jak:

• Skuteczny w oddzielaniu danych nieliniowych
• Wysoka dokładność zarówno w niższych, jak i wyższych przestrzeniach wymiarowych
• Odporny na problem nadmiernego dopasowania, ponieważ wektory nośne wpływają tylko na położenie hiperpłaszczyzny.

Sprawdź: 6 rodzajów funkcji aktywacji w sieciach neuronowych, które musisz znać

Podsumowując

Szczegółowo przyjrzeliśmy się algorytmowi maszyny wektorów nośnych w tym artykule. Dowiedzieliśmy się o algorytmie SVM , jego działaniu, jego typach, zastosowaniach, zaletach i implementacji w Pythonie. Ten artykuł da Ci podstawowe pojęcie o algorytmie SVM i odpowie na niektóre z Twoich pytań.

Ale przyniesie to również kilka innych pytań, takich jak to, w jaki sposób algorytm SVM wie, która jest właściwa płaszczyzna hiperpłaszczyznowa, jakie inne biblioteki są dostępne w Pythonie i gdzie znaleźć treningowy zestaw danych? Jeśli chcesz dowiedzieć się więcej o uczeniu maszynowym, sprawdź dyplom PG IIIT-B i upGrad w uczeniu maszynowym i sztucznej inteligencji, który jest przeznaczony dla pracujących profesjonalistów i oferuje ponad 450 godzin rygorystycznego szkolenia, ponad 30 studiów przypadków i zadań, IIIT- Status absolwenta B, ponad 5 praktycznych, praktycznych projektów zwieńczenia i pomoc w pracy z najlepszymi firmami.