機械学習でのサポートベクターマシンアルゴリズム

サポートベクターマシンアルゴリズムについて知っておくべきことすべて

ほとんどの初心者は、機械学習に関しては、当然、回帰および分類アルゴリズムから始めます。 これらのアルゴリズムはシンプルで従うのが簡単です。 ただし、機械学習の概念をよりよく理解するには、これら2つの機械学習アルゴリズムを超えることが不可欠です。

機械学習では学ぶべきことがたくさんあります。これは回帰や分類ほど単純ではないかもしれませんが、さまざまな複雑な問題を解決するのに役立ちます。 そのようなアルゴリズムの1つであるサポートベクターマシンアルゴリズムを紹介しましょう。 サポートベクターマシンアルゴリズム、またはSVMアルゴリズムは、通常、回帰と分類の両方の問題に対して効率と精度を提供できる機械学習アルゴリズムの1つと呼ばれます。

機械学習の分野でのキャリアを追求することを夢見ている場合は、サポートベクターマシンを学習の武器の一部にする必要があります。 upGradでは、学生がキャリアを開始するための最高の機械学習アルゴリズムを備えていると信じています。 機械学習でSVMアルゴリズムを開始するのに役立つと思われるものは次のとおりです。

サポートベクターマシンアルゴリズムとは何ですか？

SVMは、2020年に非常に人気があり、今後も普及し続ける教師あり学習アルゴリズムの一種です。 SVMの歴史は1990年にさかのぼります。 それはヴァプニクの統計的学習理論から引き出されています。 SVMは、回帰と分類の両方の課題に使用できます。 ただし、主に分類の課題に対処するために使用されます。

SVMは、N次元空間に超平面を作成する識別分類器です。ここで、nは、将来のデータ入力を識別するのに役立つデータセット内の特徴の数です。 紛らわしいように聞こえますが、心配しないでください。簡単な素人の言葉で理解します。

サポートベクターマシンアルゴリズムはどのように機能しますか？

SVMの動作を深く掘り下げる前に、いくつかの重要な用語を理解しましょう。

超平面

超平面は、決定境界または決定平面とも呼ばれ、データポイントの分類に役立つ境界です。 新しいデータポイントが位置する超平面の側は、分離するか、さまざまなクラスに関連付けることができます。 超平面の次元は、データセットに起因するフィーチャの数によって異なります。 データセットに2つの特徴がある場合、超平面は単純な線にすることができます。 データセットに3つの特徴がある場合、超平面は2次元平面です。

サポートベクター

サポートベクターは、超平面に最も近く、その位置に影響を与えるデータポイントです。 これらのベクトルは超平面の位置決めに影響を与えるため、サポートベクターと呼ばれ、サポートベクターマシンアルゴリズムと呼ばれます。

マージン

簡単に言えば、マージンは超平面とサポートベクターの間のギャップです。 SVMは常に、マージンを最大化する超平面を選択します。 マージンが大きいほど、結果の精度は高くなります。 SVMアルゴリズムで使用されるマージンには、ハードとソフトの2種類があります。

トレーニングデータセットが線形分離可能である場合、SVMは限界距離を最大化する2本の平行線を選択するだけです。 これはハードマージンと呼ばれます。 トレーニングデータセットが完全に線形に分離されていない場合、SVMはマージン違反を許可します。 これにより、一部のデータポイントが超平面の反対側、またはマージンと超平面の間に留まることができるため、精度が損なわれることはありません。 これはソフトマージンと呼ばれます。

特定のデータセットには、多くの可能な超平面が存在する可能性があります。 VSMの目標は、新しいデータポイントをさまざまなクラスに分類するために、最大のマージンを選択することです。 新しいデータポイントが追加されると、SVMはデータポイントが超平面のどちら側にあるかを判断します。 次に、新しいデータポイントが位置する超平面の側面に基づいて、SVMはそれをさまざまなクラスに分類します。

読む：機械学習の線形代数：重要な概念、MLの前に学ぶ理由

サポートベクターマシンの種類は何ですか？

トレーニングデータセットに基づいて、 SVMアルゴリズムには次の2つのタイプがあります。

線形SVM

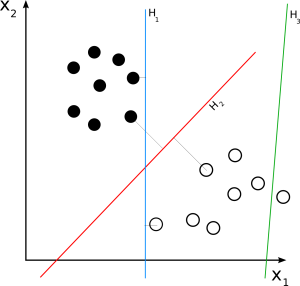
ソース

線形SVMは、線形分離可能なデータセットに使用されます。 簡単な実例は、線形SVMの動作を理解するのに役立ちます。 人の体重という単一の特徴を持つデータセットについて考えてみます。 データポイントは、肥満または非肥満の2つのクラスに分類されると想定できます。 データポイントをこれらの2つのクラスに分類するために、SVMは、最も近いサポートベクターを使用して最大マージンの超平面を作成できます。 これで、新しいデータポイントが追加されるたびに、SVMは超平面の落下する側を検出し、その人を肥満かどうかに分類します。

非線形SVM

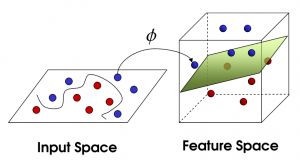
ソース

特徴の数が増えると、データセットを直線的に分離することが困難になります。 ここで、非線形SVMが使用されます。 データセットが線形分離可能でない場合、データポイントを分離するために直線を描くことはできません。 したがって、これらのデータポイントを分離するために、SVMは別の次元を追加します。 新しい次元zは、z = x2+Y2として計算できます。 この計算は、データセットの特徴を線形形式で分離するのに役立ち、SVMはデータポイントを分類するための超平面を作成できます。

新しい次元を追加してデータポイントを高次元空間に変換すると、超平面で簡単に分離できるようになります。 これは、いわゆるカーネルトリックの助けを借りて行われます。 カーネルトリックを使用すると、 SVMアルゴリズムは分離不可能なデータを分離可能なデータに変換できます。

カーネルとは何ですか？

カーネルは、低次元の入力を受け取り、それらを高次元の空間に変換する関数です。 これは、SVM出力の精度を高めるのに役立つチューニングパラメーターとも呼ばれます。 それらは、いくつかの複雑なデータ変換を実行して、分離不可能なデータセットを分離可能なデータセットに変換します。

ソース

SVMカーネルのさまざまなタイプは何ですか？

線形カーネル

名前が示すように、線形カーネルは線形分離可能なデータセットに使用されます。 これは主に、すべてのアルファベットが新しい機能であるテキスト分類など、多数の機能を備えたデータセットに使用されます。 線形カーネルの構文は次のとおりです。

K（x、y）= sum（x * y）

構文のxとyは2つのベクトルです。

線形カーネルを使用したSVMのトレーニングは、ガンマパラメーターではなくC正則化パラメーターのみの最適化を必要とするため、他のカーネルを使用したトレーニングよりも高速です。

多項式カーネル

多項式カーネルは、非線形データセットの変換に役立つ線形カ​​ーネルのより一般化された形式です。 多項式カーネルの式は次のとおりです。

K（x、y）=（xT * y + c）d

ここで、xとyは2つのベクトル、cは高次元と低次元の項のトレードオフを可能にする定数、dはカーネルの次数です。 開発者は、アルゴリズムでカーネルの順序を手動で決定することになっています。

動径基底関数カーネル

動径基底関数カーネルは、ガウスカーネルとも呼ばれ、分類問題を解決するためにSVMアルゴリズムで広く使用されているカーネルです。 入力データを無期限の高次元空間にマッピングする可能性があります。 動径基底関数カーネルは、数学的に次のように表すことができます。

K（x、y）= exp（-gamma * sum（x – y2））

ここで、xとyは2つのベクトルであり、ガンマは0から1の範囲の調整パラメーターです。ガンマは学習アルゴリズムで手動で事前定義されています。

線形、多項式、および放射基底関数は、超平面作成の決定と精度を行うための数学的アプローチが異なります。 線形カーネルと多項式カーネルは、トレーニングにかかる​​時間が短くなりますが、精度は低くなります。 一方、動径基底関数カーネルはトレーニングに時間がかかりますが、結果の点でより高い精度を提供します。

ここで発生する問題は、データセットに使用するカーネルをどのように選択するかです。 決定は、データセットの複雑さと必要な結果の精度にのみ依存する必要があります。 もちろん、誰もが高精度の結果を望んでいますが、それはソリューションを開発するために必要な時間とそれに費やすことができる金額にも依存します。 また、動径基底関数カーネルは一般に高い精度を提供しますが、状況によっては、線形カーネルと多項式カーネルが同等にうまく機能する場合があります。

たとえば、線形分離可能なデータの場合、線形カーネルは動径基底カーネルと同様に機能し、トレーニング時間も少なくて済みます。 したがって、データセットが線形分離可能である場合は、線形カーネルを選択する必要があります。 非線形データの場合、時間と費用に応じて、多項式または放射基底関数を選択する必要があります。

カーネルで使用されるチューニングパラメータは何ですか？

C正則化

C正則化パラメーターは、各トレーニングデータセットで特定のレベルの誤分類を許可するために、ユーザーからの値を受け入れます。 より高いC正則化値は、マージンの小さい超平面につながり、多くの誤分類を許容しません。 一方、値を低くすると、マージンが高くなり、誤分類が大きくなります。

ガンマ

ガンマパラメータは、超平面の配置に影響を与えるサポートベクターの範囲を定義します。 高いガンマ値は近くのデータポイントのみを考慮し、低い値は遠くのポイントを考慮します。

Pythonでサポートベクターマシンアルゴリズムを実装する方法は？

ソース

SVMアルゴリズムとは何か、そしてそれがどのように機能するかについての基本的な考え方があるので、もっと複雑なことを掘り下げてみましょう。 次に、PythonでSVMアルゴリズムを実装して実行するための一般的な手順を見ていきます。 PythonのScikit-Learnライブラリを使用して、 SVMアルゴリズムの実装方法を学習します。

まず第一に、 SVMアルゴリズムを実行するために必要なPandasやNumPyなどの必要なすべてのライブラリをインポートする必要があります。 すべてのライブラリを配置したら、トレーニングデータセットをインポートする必要があります。 次に、データセットを分析する必要があります。 データセットを分析する方法は複数あります。

たとえば、データのディメンションを確認し、それを応答変数と説明変数に分割し、KPIを設定してデータセットを分析できます。 データ分析が完了したら、データセットを前処理する必要があります。 データセット内の無関係、不完全、および不正確なデータをチェックする必要があります。

次に、トレーニングの部分があります。 関連するカーネルを使用してアルゴリズムをコーディングおよびトレーニングする必要があります。 Scikit-LearnにはSVMライブラリが含まれており、アルゴリズムをトレーニングするための組み込みクラスがいくつかあります。 SVMライブラリには、アルゴリズムのトレーニングに使用するカーネルのタイプの値を受け入れるSVCクラスが含まれています。

次に、アルゴリズムをトレーニングするSVCクラスのfitメソッドを呼び出し、fitメソッドのパラメーターとして挿入します。 次に、SVCクラスのpredictメソッドを使用して、アルゴリズムの予測を行う必要があります。 予測ステップが完了したら、メトリックライブラリのclassification_reportとconfusion_matrixを呼び出して、アルゴリズムを評価し、結果を確認する必要があります。

サポートベクターマシンアルゴリズムのアプリケーションは何ですか？

SVMアルゴリズムには、さまざまな回帰および分類の課題にまたがるアプリケーションがあります。 SVMアルゴリズムの主要なアプリケーションのいくつかは次のとおりです。

• テキストとハイパーテキストの分類
• 画像分類
• 合成開口レーダー（SAR）などの衛星データの分類
• タンパク質などの生物学的物質の分類
• 手書きテキストでの文字認識

サポートベクターマシンアルゴリズムを使用する理由

SVMアルゴリズムには、次のようなさまざまな利点があります。

• 非線形データの分離に効果的
• 低次元空間と高次元空間の両方で高精度
• サポートベクターは超平面の位置にのみ影響を与えるため、過剰適合の問題に耐性があります。

チェックアウト：知っておく必要のあるニューラルネットワークの6種類の活性化関数

まとめ

この記事では、サポートベクターマシンアルゴリズムについて詳しく見てきました。 SVMアルゴリズム、その仕組み、タイプ、アプリケーション、利点、Pythonでの実装について学びました。 この記事では、 SVMアルゴリズムの基本的な考え方を説明し、いくつかの質問に答えます。

しかし、 SVMアルゴリズムが正しい超平面がどれであるかをどのように知るか、Pythonで利用できる他のライブラリは何か、トレーニングデータセットをどこで見つけるかなど、他のいくつかの質問ももたらします。 機械学習について詳しく知りたい場合は、IIIT-BとupGradの機械学習とAIのPGディプロマをご覧ください。これは、働く専門家向けに設計されており、450時間以上の厳格なトレーニング、30以上のケーススタディと課題、IIIT-を提供します。 B卒業生のステータス、5つ以上の実践的なキャップストーンプロジェクト、トップ企業との仕事の支援。