Prise en charge de l'algorithme de machine vectorielle dans l'apprentissage automatique

Tout ce que vous devez savoir sur les algorithmes de machines à vecteurs de support

La plupart des débutants, en matière d'apprentissage automatique, commencent naturellement par les algorithmes de régression et de classification . Ces algorithmes sont simples et faciles à suivre. Cependant, il est essentiel d'aller au-delà de ces deux algorithmes de machine learning pour mieux appréhender les concepts de machine learning.

Il y a beaucoup plus à apprendre dans l'apprentissage automatique, ce qui n'est peut-être pas aussi simple que la régression et la classification, mais peut nous aider à résoudre divers problèmes complexes. Laissez-nous vous présenter l'un de ces algorithmes, le Support Vector Machine Algorithm . L'algorithme Support Vector Machine , ou algorithme SVM , est généralement désigné comme l'un de ces algorithmes d'apprentissage automatique qui peut offrir efficacité et précision pour les problèmes de régression et de classification.

Si vous rêvez de poursuivre une carrière dans le domaine de l'apprentissage automatique, alors la machine vectorielle de support devrait faire partie de votre arsenal d'apprentissage. Chez upGrad , nous croyons qu'il est important de doter nos étudiants des meilleurs algorithmes d'apprentissage automatique pour démarrer leur carrière. Voici ce que nous pensons pouvoir vous aider à démarrer avec l' algorithme SVM dans l'apprentissage automatique.

Qu'est-ce qu'un algorithme de machine à vecteurs de support ?

SVM est un type d' algorithme d'apprentissage supervisé qui est devenu très populaire en 2020 et continuera de l'être à l'avenir. L'histoire de SVM remonte à 1990 ; il est tiré de la théorie de l'apprentissage statistique de Vapnik. SVM peut être utilisé à la fois pour les défis de régression et de classification ; cependant, il est principalement utilisé pour résoudre les problèmes de classification.

SVM est un classificateur discriminatif qui crée des hyperplans dans un espace à N dimensions, où n est le nombre d'entités dans un ensemble de données pour aider à discriminer les futures entrées de données. Cela semble déroutant, ne vous inquiétez pas, nous le comprendrons en termes simples.

Comment fonctionne un algorithme de machine à vecteur de support ?

Avant d'approfondir le fonctionnement d'un SVM, comprenons quelques-unes des terminologies clés.

Hyperplan

Les hyperplans, parfois appelés limites de décision ou plans de décision, sont les limites qui aident à classer les points de données. Le côté de l'hyperplan, où tombe un nouveau point de données, peut être séparé ou attribué à différentes classes. La dimension de l'hyperplan dépend du nombre d'entités attribuées à un jeu de données. Si le jeu de données comporte 2 entités, l'hyperplan peut être une simple ligne. Lorsqu'un jeu de données comporte 3 entités, l'hyperplan est un plan bidimensionnel.

Vecteurs de soutien

Les vecteurs de support sont les points de données les plus proches de l'hyperplan et affectent sa position. Étant donné que ces vecteurs affectent le positionnement de l'hyperplan, ils sont appelés vecteurs de support et d'où le nom d' algorithme de machine à vecteur de support.

Marge

En termes simples, la marge est l'écart entre l'hyperplan et les vecteurs de support. SVM choisit toujours l'hyperplan qui maximise la marge. Plus la marge est grande, plus la précision des résultats est élevée. Il existe deux types de marges utilisées dans les algorithmes SVM , dures et souples.

Lorsque l'ensemble de données d'apprentissage est linéairement séparable, SVM peut simplement sélectionner deux lignes parallèles qui maximisent la distance marginale ; c'est ce qu'on appelle une marge dure. Lorsque l'ensemble de données d'apprentissage n'est pas entièrement séparé de manière linéaire, la SVM autorise une certaine violation de marge. Cela permet à certains points de données de rester du mauvais côté de l'hyperplan ou entre la marge et l'hyperplan afin que la précision ne soit pas compromise ; c'est ce qu'on appelle une marge souple.

Il peut y avoir plusieurs hyperplans possibles pour un jeu de données donné. L'objectif de VSM est de sélectionner la marge la plus maximale pour classer les nouveaux points de données dans différentes classes. Lorsqu'un nouveau point de données est ajouté, la SVM détermine de quel côté de l'hyperplan le point de données tombe. En fonction du côté de l'hyperplan où se situe le nouveau point de données, SVM le classe ensuite en différentes classes.

Lire : Algèbre linéaire pour l'apprentissage automatique : concepts critiques, pourquoi apprendre avant le ML

Quels sont les types de machines à vecteurs de support ?

Sur la base de l'ensemble de données d'apprentissage, les algorithmes SVM peuvent être de deux types :

SVM linéaire

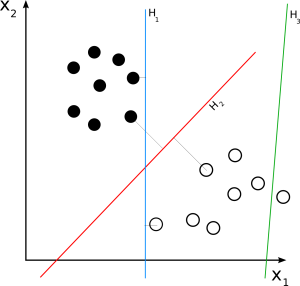
La source

Le SVM linéaire est utilisé pour un ensemble de données séparable linéairement. Un exemple simple du monde réel peut nous aider à comprendre le fonctionnement d'un SVM linéaire. Considérez un ensemble de données qui a une seule caractéristique, le poids d'une personne. Les points de données peuvent être censés être classés en deux classes, obèses ou non obèses. Pour classer les points de données dans ces deux classes, SVM peut créer un hyperplan à marge maximale à l'aide des vecteurs de support les plus proches. Désormais, chaque fois qu'un nouveau point de données est ajouté, le SVM détecte le côté de l'hyperplan, où il tombe, et classe la personne comme obèse ou non.

SVM non linéaire

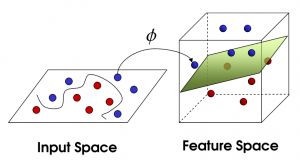
La source

À mesure que le nombre d'entités augmente, la séparation linéaire de l'ensemble de données devient difficile. C'est là qu'un SVM non linéaire est utilisé. Nous ne pouvons pas tracer une ligne droite pour séparer les points de données lorsque l'ensemble de données n'est pas linéairement séparable. Donc, pour séparer ces points de données, SVM ajoute une autre dimension. La nouvelle dimension z peut être calculée comme z = x2 + Y2. Ce calcul aidera à séparer les caractéristiques d'un ensemble de données sous forme linéaire, puis SVM pourra créer l'hyperplan pour classer les points de données.

Lorsqu'un point de données est transformé en un espace de grande dimension en ajoutant une nouvelle dimension, il devient facilement séparable avec un hyperplan. Cela se fait à l'aide de ce qu'on appelle l'astuce du noyau. Avec l'astuce du noyau, les algorithmes SVM peuvent transformer des données non séparables en données séparables.

Qu'est-ce qu'un noyau ?

Un noyau est une fonction qui prend des entrées de faible dimension et les transforme en espace de grande dimension. Il est également appelé paramètre de réglage qui aide à augmenter la précision des sorties SVM. Ils effectuent des transformations de données complexes pour convertir l'ensemble de données non séparable en un ensemble séparable.

La source

Quels sont les différents types de noyaux SVM ?

Noyau linéaire

Comme son nom l'indique, le noyau linéaire est utilisé pour les ensembles de données séparables linéairement. Il est principalement utilisé pour les ensembles de données avec un grand nombre de fonctionnalités, la classification de texte, par exemple, où tous les alphabets sont une nouvelle fonctionnalité. La syntaxe du noyau linéaire est :

K(x, y) = somme(x*y)

x et y dans la syntaxe sont deux vecteurs.

L'entraînement d'un SVM avec un noyau linéaire est plus rapide que l'entraînement avec n'importe quel autre noyau car il nécessite l'optimisation du seul paramètre de régularisation C et non du paramètre gamma.

Noyau polynomial

Le noyau polynomial est une forme plus généralisée du noyau linéaire qui est utile pour transformer un ensemble de données non linéaires. La formule du noyau polynomial est la suivante :

K(x, y) = (xT*y + c)d

Ici x et y sont deux vecteurs, c est une constante qui permet un compromis entre les termes de dimension supérieure et inférieure, et d est l'ordre du noyau. Le développeur est censé décider manuellement de l'ordre du noyau dans l'algorithme.

Noyau de fonction de base radiale

Le noyau de la fonction de base radiale, également appelé noyau gaussien, est un noyau largement utilisé dans les algorithmes SVM pour résoudre les problèmes de classification. Il a le potentiel de cartographier les données d'entrée dans des espaces de grande dimension indéfinis. Le noyau de la fonction de base radiale peut être mathématiquement représenté par :

K(x, y) = exp(-gamma*somme(x – y2))

Ici, x et y sont deux vecteurs, et gamma est un paramètre de réglage allant de 0 à 1. Gamma est prédéfini manuellement dans l'algorithme d'apprentissage.

Les fonctions de base linéaire, polynomiale et radiale diffèrent dans leur approche mathématique pour prendre les décisions de création d'hyperplan et leur précision. Les noyaux linéaires et polynomiaux consomment moins de temps en formation mais offrent moins de précision. D'autre part, le noyau de la fonction de base radiale prend plus de temps dans la formation mais offre une plus grande précision en termes de résultats.

Maintenant, la question qui se pose est de savoir comment choisir le noyau à utiliser pour votre jeu de données. Votre décision doit uniquement dépendre de la complexité de l'ensemble de données et de la précision des résultats que vous souhaitez obtenir. Bien sûr, tout le monde veut des résultats de haute précision, mais cela dépend aussi du temps dont vous disposez pour développer la solution et du montant que vous pouvez y consacrer. En outre, le noyau de la fonction de base radiale offre généralement une plus grande précision, mais dans certaines circonstances, les noyaux linéaire et polynomial peuvent fonctionner aussi bien.

Par exemple, pour des données linéairement séparables, un noyau linéaire fonctionnera aussi bien qu'un noyau à base radiale et tout en consommant moins de temps d'apprentissage. Donc, si votre jeu de données est linéairement séparable, vous devez choisir un noyau linéaire. Pour les données non linéaires, vous devez choisir une fonction de base polynomiale ou radiale en fonction du temps et des dépenses dont vous disposez.

Quels sont les paramètres de réglage utilisés avec les noyaux ?

C régularisation

Le paramètre de régularisation C accepte des valeurs de votre part pour permettre un certain niveau d'erreur de classification dans chaque ensemble de données d'apprentissage. Des valeurs de régularisation C plus élevées conduisent à un hyperplan à petite marge et ne permettent pas beaucoup d'erreurs de classification. Des valeurs plus faibles, en revanche, entraînent une marge élevée et une plus grande erreur de classification.

Gamma

Le paramètre gamma définit la plage des vecteurs de support qui auront un impact sur le positionnement de l'hyperplan. Une valeur gamma élevée ne prend en compte que les points de données proches et une valeur faible prend en compte les points éloignés.

Comment implémenter l'algorithme Support Vector Machine en Python ?

La source

Puisque nous avons l'idée de base de ce qu'est l' algorithme SVM et de son fonctionnement, plongeons dans quelque chose de plus complexe. Nous allons maintenant examiner les étapes générales pour implémenter et exécuter l' algorithme SVM en Python. Nous utiliserons la bibliothèque Scikit-Learn de Python pour apprendre à implémenter l' algorithme SVM.

Tout d'abord, nous devons importer toutes les bibliothèques nécessaires telles que Pandas et NumPy qui sont nécessaires pour exécuter les algorithmes SVM. Une fois que nous avons toutes les bibliothèques à la place, nous devons importer l'ensemble de données d'entraînement. Ensuite, nous devons analyser notre ensemble de données. Il existe plusieurs façons d'analyser un jeu de données.

Par exemple, nous pouvons vérifier les dimensions des données, les diviser en variables de réponse et explicatives, et définir des KPI pour analyser notre ensemble de données. Après avoir terminé l'analyse des données, nous devons pré-traiter l'ensemble de données. Nous devons vérifier les données non pertinentes, incomplètes et incorrectes dans notre ensemble de données.

Vient maintenant la partie formation. Nous devons coder et former notre algorithme avec le noyau approprié. Le Scikit-Learn contient la bibliothèque SVM, où vous pouvez trouver des classes intégrées pour les algorithmes de formation. La bibliothèque SVM contient une classe SVC qui accepte la valeur du type de noyau que vous souhaitez utiliser pour entraîner vos algorithmes.

Ensuite, vous appelez la méthode fit de la classe SVC qui entraîne votre algorithme, insérée en tant que paramètre de la méthode fit. Vous devez ensuite utiliser la méthode predict de la classe SVC pour faire des prédictions pour l'algorithme. Une fois que vous avez terminé l'étape de prédiction, vous devez appeler le classification_report et confusion_matrix de la bibliothèque de métriques pour évaluer votre algorithme et voir le résultat.

Quelles sont les applications de l'algorithme Support Vector Machine ?

Les algorithmes SVM ont des applications dans divers défis de régression et de classification. Certaines des applications clés des algorithmes SVM sont :

• Classification de texte et d'hypertexte
• Classement des images
• Classification des données satellitaires telles que le radar à synthèse d'ouverture (SAR)
• Classification des substances biologiques telles que les protéines
• Reconnaissance de caractères dans un texte manuscrit

Pourquoi utiliser l'algorithme de machine à vecteur de support ?

L'algorithme SVM offre divers avantages tels que :

• Efficace pour séparer les données non linéaires
• Très précis dans les espaces dimensionnels inférieurs et supérieurs
• Insensible au problème de surajustement car les vecteurs de support n'impactent que la position de l'hyperplan.

Découvrez : 6 types de fonction d'activation dans les réseaux de neurones que vous devez connaître

Résumé

Nous avons examiné en détail l' algorithme de la machine à vecteurs de support dans cet article. Nous avons découvert l' algorithme SVM , son fonctionnement, ses types, ses applications, ses avantages et sa mise en œuvre en Python. Cet article vous donnera une idée de base sur l' algorithme SVM et répondra à certaines de vos questions.

Mais cela apportera également d'autres questions telles que comment l' algorithme SVM sait quel est le bon hyperplan, quelles sont les autres bibliothèques disponibles en Python et où trouver l'ensemble de données d'entraînement ? Si vous souhaitez en savoir plus sur l'apprentissage automatique, consultez le diplôme PG en apprentissage automatique et IA de IIIT-B & upGrad, conçu pour les professionnels en activité et offrant plus de 450 heures de formation rigoureuse, plus de 30 études de cas et missions, IIIT- Statut B Alumni, plus de 5 projets de synthèse pratiques et aide à l'emploi avec les meilleures entreprises.