Sinir Ağı: Mimari, Bileşenler ve En İyi Algoritmalar

Yapay Sinir Ağları (YSA), Derin Öğrenme sürecinin ayrılmaz bir parçasını oluşturur. İnsan beyninin nörolojik yapısından ilham alıyorlar. AILabPage'e göre , YSA'lar "insan beyni çalışma ve veri işleme (Bilgi) modellerini simüle etmek için insan biyolojik beyin yapısından ilham alan, basit, yüksek düzeyde birbirine bağlı işlem öğelerinin sayısıyla yazılmış karmaşık bilgisayar kodudur."

Kariyerinizi hızlandırmak için Dünyanın En İyi Üniversiteleri - Yüksek Lisanslar, Yönetici Yüksek Lisans Programları ve Makine Öğrenimi ve Yapay Zeka alanında Gelişmiş Sertifika Programı'ndan çevrimiçi En İyi Makine Öğrenimi Sertifikalarına katılın .

Derin Öğrenme, aşağıdakiler de dahil olmak üzere beş temel Sinir Ağına odaklanır:

• Çok Katmanlı Algılayıcı
• Radyal Tabanlı Ağ
• Tekrarlayan Sinir Ağları
• Üretken Düşman Ağları
• Evrişimli Sinir Ağları.

Sinir Ağı: Mimari

Sinir Ağları, tek bir çıktı üretmek için birden fazla girdi alabilen yapay nöronlardan oluşan karmaşık yapılardır. Girdiyi anlamlı bir çıktıya dönüştürmek, bir Sinir Ağının birincil işidir. Genellikle, bir Sinir Ağı, içinde bir veya daha fazla gizli katman bulunan bir giriş ve çıkış katmanından oluşur.

Bir Sinir Ağında, tüm nöronlar birbirini etkiler ve bu nedenle hepsi birbirine bağlıdır. Ağ, eldeki veri kümesinin her yönünü ve verinin farklı bölümlerinin birbiriyle nasıl ilişkili olabileceğini veya olmayabileceğini kabul edebilir ve gözlemleyebilir. Yapay Sinir Ağları bu şekilde çok büyük veri hacimlerinde son derece karmaşık kalıpları bulabilmektedir.

Okuyun: Yapay Sinir Ağları ve Makine Öğrenimi

Bir Sinir Ağında bilgi akışı iki şekilde gerçekleşir -

• İleri Beslemeli Ağlar: Bu modelde, sinyaller çıkış katmanına doğru yalnızca bir yönde hareket eder. İleri Beslemeli Ağlar, bir giriş katmanına ve sıfır veya birden çok gizli katmana sahip tek bir çıkış katmanına sahiptir. Örüntü tanımada yaygın olarak kullanılırlar.
• Geri Besleme Ağları: Bu modelde, tekrarlayan veya etkileşimli ağlar, girdi sırasını işlemek için dahili durumlarını (belleklerini) kullanır. Onlarda, sinyaller ağdaki döngüler (gizli katman/lar) boyunca her iki yönde de hareket edebilir. Genellikle zaman serisi ve sıralı görevlerde kullanılırlar.

Sinir Ağı: Bileşenler

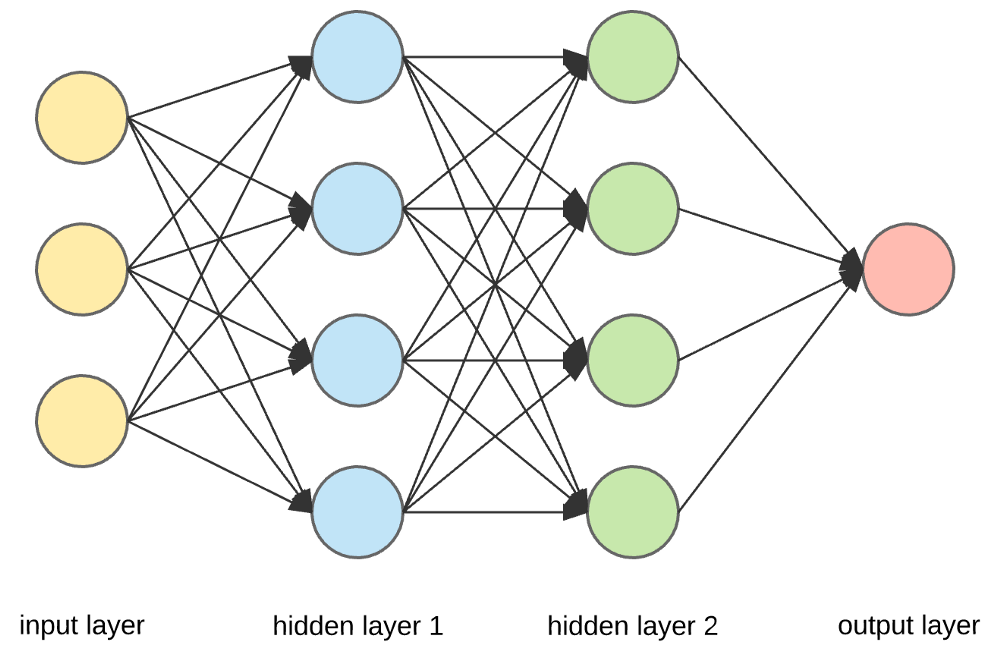
Kaynak

Girdi Katmanları, Nöronlar ve Ağırlıklar –

Yukarıda verilen resimde en dıştaki sarı katman giriş katmanıdır. Bir nöron, bir sinir ağının temel birimidir. Harici bir kaynaktan veya diğer düğümlerden girdi alırlar. Her düğüm, bir sonraki katmandan başka bir düğümle bağlantılıdır ve bu tür bağlantıların her birinin belirli bir ağırlığı vardır. Ağırlıklar, diğer girdilere göre göreceli önemine göre bir nörona atanır.

Sarı katmandaki tüm düğüm değerleri (ağırlıklarıyla birlikte) çarpılıp özetlendiğinde, ilk gizli katman için bir değer üretir. Özetlenen değere bağlı olarak, mavi katman, bu düğümün "etkinleştirilip etkinleştirilmeyeceğini" ve ne kadar "etkin" olacağını belirleyen önceden tanımlanmış bir "etkinleştirme" işlevine sahiptir.

Bunu basit bir günlük görev kullanarak anlayalım – çay yapmak. Çay yapım sürecinde çay yapımında kullanılan malzemeler (su, çay yaprağı, süt, şeker ve baharatlar) sürecin başlangıç ​​noktalarını oluşturdukları için “nöronlar”dır. Her bir bileşenin miktarı “ağırlığı” temsil eder. Çay yapraklarını suya atıp şekeri, baharatları ve sütü tencereye ekledikten sonra tüm malzemeler karışacak ve başka bir hal alacaktır. Bu dönüşüm süreci “aktivasyon fonksiyonunu” temsil eder.

Hakkında bilgi edinin: Derin Öğrenme ve Sinir Ağları

Gizli Katmanlar ve Çıktı Katmanı –

Giriş ve çıkış katmanı arasında gizlenen katman veya katmanlar, gizli katman olarak bilinir. Her zaman dış dünyadan gizlendiği için gizli katman olarak adlandırılır. Bir Sinir Ağının ana hesaplaması gizli katmanlarda gerçekleşir. Böylece gizli katman, girdi katmanından tüm girdileri alır ve bir sonuç üretmek için gerekli hesaplamayı yapar. Bu sonuç daha sonra çıktı katmanına iletilir, böylece kullanıcı hesaplamanın sonucunu görebilir.

Çay yapma örneğimizde, tüm malzemeleri karıştırdığımızda, formülasyon ısıtma sırasında durumunu ve rengini değiştirir. Malzemeler gizli katmanları temsil eder. Burada ısıtma, sonunda sonucu veren aktivasyon sürecini temsil eder - çay.

Sinir Ağı: Algoritmalar

Bir Sinir Ağında, öğrenme (veya eğitim) süreci, verileri üç farklı kümeye bölerek başlatılır:

• Eğitim veri seti – Bu veri seti, Sinir Ağının düğümler arasındaki ağırlıkları anlamasını sağlar.
• Doğrulama veri seti – Bu veri seti, Sinir Ağı performansının ince ayarını yapmak için kullanılır.
• Test veri seti – Bu veri seti, Sinir Ağının doğruluğunu ve hata payını belirlemek için kullanılır.

Veriler bu üç parçaya bölündükten sonra, Sinir Ağını eğitmek için onlara Sinir Ağı algoritmaları uygulanır. Bir Sinir Ağında eğitim sürecini kolaylaştırmak için kullanılan prosedür optimizasyon olarak bilinir ve kullanılan algoritmaya optimizer denir. Her biri kendine özgü özellikleri ve bellek gereksinimleri, sayısal kesinlik ve işlem hızı gibi yönleri olan farklı türde optimizasyon algoritmaları vardır.

Farklı Sinir Ağı algoritmalarının tartışmasına dalmadan önce, önce öğrenme problemini anlayalım.

Ayrıca okuyun : Gerçek Dünyada Sinir Ağı Uygulamaları

Öğrenme Problemi Nedir?

Öğrenme problemini bir kayıp indeksinin ( f ) minimizasyonu açısından temsil ediyoruz . Burada “ f ”, bir Sinir Ağının belirli bir veri seti üzerindeki performansını ölçen fonksiyondur. Genel olarak, kayıp indeksi bir hata terimi ve bir düzenleme teriminden oluşur. Hata terimi , bir Sinir Ağının bir veri kümesine nasıl uyduğunu değerlendirirken, düzenleme terimi , Sinir Ağının etkin karmaşıklığını kontrol ederek aşırı uyum sorununun önlenmesine yardımcı olur.

Kayıp fonksiyonu [ f(w ], Sinir Ağının uyarlanabilir parametrelerine – ağırlıklar ve önyargılar – bağlıdır.Bu parametreler tek bir n-boyutlu ağırlık vektörü ( w ) halinde gruplandırılabilir.

İşte kayıp fonksiyonunun resimli bir temsili:

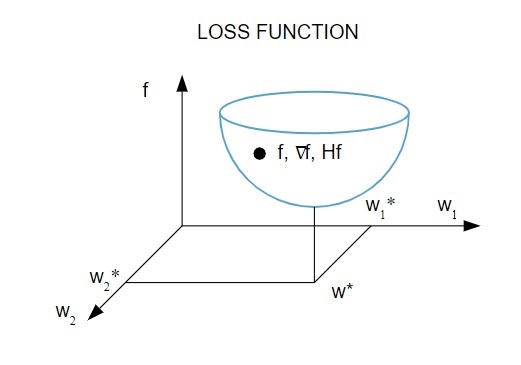
Kaynak

Bu diyagrama göre kayıp fonksiyonunun minimumu ( w* ) noktasında gerçekleşir . Herhangi bir noktada kayıp fonksiyonunun birinci ve ikinci türevlerini hesaplayabilirsiniz. İlk türevler gradyan vektöründe gruplandırılmıştır ve bileşenleri şu şekilde gösterilmiştir:

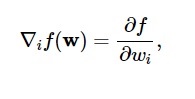
Kaynak

Burada, i = 1,…..,n .

Kayıp fonksiyonunun ikinci türevleri Hessian matrisinde şu şekilde gruplandırılmıştır:

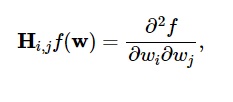
Kaynak

Burada, i,j = 0,1,…

Artık öğrenme probleminin ne olduğunu bildiğimize göre, beş ana konuyu tartışabiliriz.

Sinir Ağı algoritmaları .

1. Tek boyutlu optimizasyon

Kayıp fonksiyonu birden fazla parametreye bağlı olduğundan , tek boyutlu optimizasyon yöntemleri Sinir Ağı eğitiminde etkilidir. Eğitim algoritmaları önce bir eğitim yönü ( d ) hesaplar ve ardından eğitim yönündeki kaybı en aza indirmeye yardımcı olan eğitim oranını ( η ) hesaplar [ f(η) ].

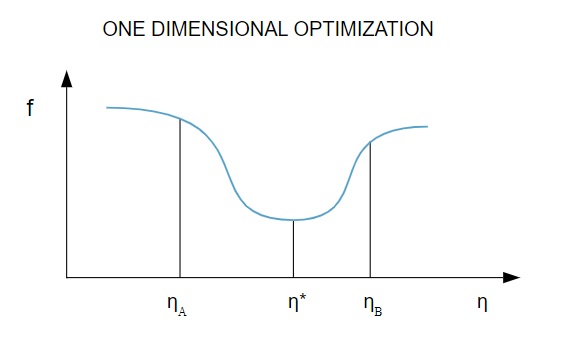
Kaynak

Diyagramda, η1 ve η2 noktaları, f, η* minimumunu içeren aralığı tanımlar .

Böylece, tek boyutlu optimizasyon yöntemleri, verilen bir boyutlu fonksiyonun minimumunu bulmayı amaçlar. En yaygın kullanılan tek boyutlu algoritmalardan ikisi Altın Kesit Yöntemi ve Brent Yöntemidir.

Altın Kesit Yöntemi

Altın bölüm arama algoritması, tek değişkenli bir fonksiyonun minimum veya maksimumunu bulmak için kullanılır [ f(x) ]. Bir fonksiyonun iki nokta arasında minimumu olduğunu zaten biliyorsak, f(x) = 0 denkleminin kökünü ikiye bölme aramasında yaptığımız gibi yinelemeli bir arama yapabiliriz . Ayrıca, minimumun komşuluğunda f(x0) > f(x1) > f(X2)'ye karşılık gelen üç nokta ( x0 < x1 < x2 ) bulabilirsek, o zaman x0 ile x2 arasında bir minimumun var olduğu sonucunu çıkarabiliriz. . Bu minimumu bulmak için, x1 ve x2 arasındaki başka bir x3 noktasını düşünebiliriz ve bu bize aşağıdaki sonuçları verecektir:

• f (x3) = f3a > f(x1) ise , minimum, x3 – x0 = a + c aralığının içindedir ve bu, üç yeni nokta x0 < x1 < x3 ile ilişkilidir (burada x2 , x3 ile değiştirilir ).
• f (x3) = f3b > f(x1 ) ise, minimum, x2 – x1 = b aralığının içindedir ve üç yeni nokta x1 < x3 < x2 ile ilişkilidir (burada x0 , x1 ile değiştirilir ).

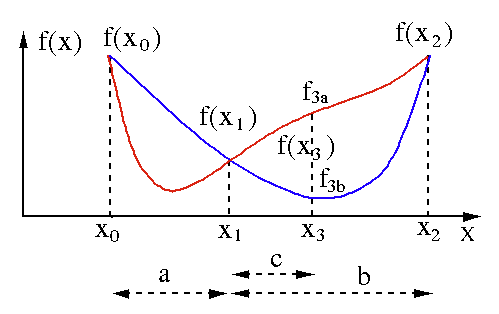
Kaynak

Brent'in Yöntemi

Brent'in yöntemi, kök parantezleme , ikiye bölme , sekant ve ters ikinci dereceden enterpolasyonu birleştiren bir kök bulma algoritmasıdır . Bu algoritma, mümkün olduğunda hızlı yakınsayan sekant yöntemini veya ters ikinci dereceden enterpolasyonu kullanmaya çalışsa da, genellikle ikiye bölme yöntemine geri döner. Wolfram Dilinde uygulanan Brent'in yöntemi şu şekilde ifade edilir:

Yöntem -> FindRoot'ta Brent [eqn, x, x0, x1].

Brent'in yönteminde, 2. dereceden bir Lagrange interpolasyon polinomu kullanıyoruz . 1973'te Brent, fonksiyonun değerlerinin bir kök de dahil olmak üzere belirli bir bölge içinde hesaplanabilmesi koşuluyla, bu yöntemin her zaman yakınsayacağını iddia etti. Üç nokta x1, x2 ve x3 varsa , Brent'in yöntemi , interpolasyon formülünü kullanarak x'e y'nin ikinci dereceden bir işlevi olarak uyar:

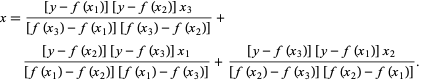
Kaynak

Sonraki kök tahminleri, dikkate alınarak elde edilir, böylece aşağıdaki denklem üretilir:

Kaynak

Burada P = S [ T(R – T) (x3 – x2) – (1 – R) (x2 -x1) ] ve Q = (T – 1) (R – 1) (S – 1) ve,

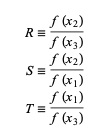
Kaynak

2. Çok boyutlu optimizasyon

Şimdiye kadar, Sinir Ağları için öğrenme probleminin , kayıp fonksiyonunun ( f ) minimum bir değer aldığı parametre vektörünü ( w* ) bulmayı amaçladığını zaten biliyoruz . Standart koşulun yetkilerine göre, Sinir Ağı kayıp fonksiyonunun minimumundaysa, gradyan sıfır vektörüdür.

Kayıp fonksiyonu parametrelerin lineer olmayan bir fonksiyonu olduğu için minimum için kapalı eğitim algoritmalarını bulmak imkansızdır. Ancak, bir dizi adım içeren parametre uzayında aramayı düşünürsek, her adımda, Sinir Ağının parametrelerini ayarlayarak kayıp azalacaktır.

Çok boyutlu optimizasyonda, bir Yapay Sinir Ağı, rastgele bir biz parametre vektörü seçilerek ve ardından algoritmanın her yinelemesinde kayıp fonksiyonunun azalmasını sağlamak için bir dizi parametre üretilerek eğitilir. Sonraki iki adım arasındaki bu kayıp varyasyonu “kayıp azalması” olarak bilinir. Kayıp azaltma süreci, eğitim algoritması belirlenen koşula ulaşana veya sağlanana kadar devam eder.

İşte çok boyutlu optimizasyon algoritmalarının üç örneği:

Dereceli alçalma

Gradyan iniş algoritması, muhtemelen tüm eğitim algoritmalarının en basitidir. Gradyan vektöründen sağlanan bilgiye dayandığı için birinci dereceden bir yöntemdir. Bu yöntemde f[w(i)] = f(i) ve ∇f[w(i)] = g(i) alacağız . Bu eğitim algoritmasının başlangıç ​​noktası, belirtilen kriter sağlanana kadar ilerlemeye devam eden w(0)'dır – w(i)'den w(i+1)' e d(i) = −g(i) eğitim yönünde hareket eder. . Bu nedenle, gradyan inişi aşağıdaki gibi yinelenir:

w(i+1) = w(i)−g(i)η(i),

Burada, i = 0,1,…

η parametresi eğitim oranını temsil eder. η için sabit bir değer ayarlayabilir veya her adımda eğitim yönü boyunca tek boyutlu optimizasyon tarafından bulunan değere ayarlayabilirsiniz. Ancak her adımda hat minimizasyonu ile elde edilen eğitim oranı için optimal değerin ayarlanması tercih edilir.

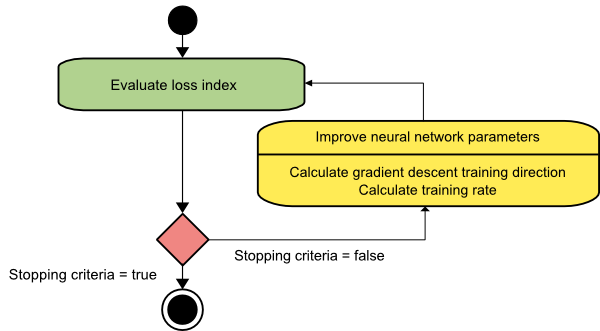
Kaynak

Bu algoritma, uzun ve dar vadi yapılarına sahip fonksiyonlar için çok sayıda iterasyon gerektirdiğinden birçok sınırlamaya sahiptir. Kayıp fonksiyonu en hızlı yokuş aşağı eğim yönünde azalırken, her zaman en hızlı yakınsamayı sağlamaz.

Newton'un yöntemi

Bu, Hessian matrisinden yararlandığı için ikinci dereceden bir algoritmadır. Newton'un yöntemi, kayıp fonksiyonunun ikinci türevlerini kullanarak daha iyi eğitim yönleri bulmayı amaçlar. Burada f[w(i)] = f(i), ∇f[w(i)]=g(i) , ve Hf[w(i)] = H(i) 'yi belirteceğiz . Şimdi, Taylor'ın seri açılımını kullanarak f'nin w(0) 'daki ikinci dereceden yaklaşımını şu şekilde ele alacağız :

f = f(0)+g(0)⋅[w−w(0)] + 0,5⋅[w−w(0)]2⋅H(0)

Burada H(0) , w(0) noktasında hesaplanan f'nin Hessian matrisidir . f(w)' nin minimumu için g = 0'ı dikkate alarak aşağıdaki denklemi elde ederiz:

g = g(0)+H(0)⋅(w−w(0))=0

Sonuç olarak, w(0) parametre vektöründen başlayarak Newton'un yönteminin aşağıdaki gibi yinelendiğini görebiliriz:

w(i+1) = w(i)−H(i)−1⋅g(i)

Burada, i = 0,1 ,… ve H(i)−1⋅g(i) vektörüne “Newton Adımı” denir. Parametre değişikliğinin minimum yönünde gitmek yerine maksimuma doğru hareket edebileceğini unutmamalısınız. Genellikle bu, Hessian matrisi pozitif tanımlı değilse olur ve bu nedenle her yinelemede fonksiyon değerlendirmesinin azalmasına neden olur. Ancak, bu sorunu önlemek için genellikle yöntem denklemini aşağıdaki gibi değiştiririz:

w(i+1) = w(i)−(H(i)−1⋅g(i))η

Burada, i = 0,1 ,….

Eğitim oranını η sabit bir değere veya hat minimizasyonu ile elde edilen değere ayarlayabilirsiniz. Böylece, d(i)=H(i)−1⋅g(i) vektörü Newton'un yöntemi için eğitim yönü olur.

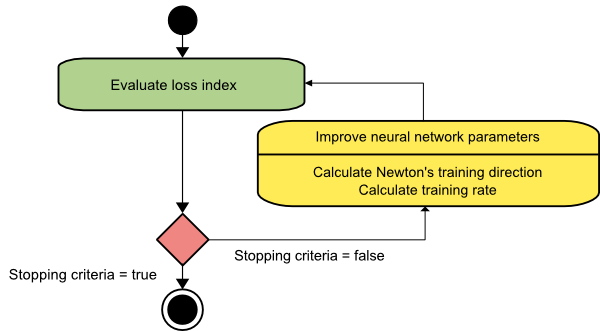
Kaynak

Newton'un yönteminin en büyük dezavantajı, Hessian ve tersinin kesin değerlendirmesinin oldukça pahalı hesaplamalar olmasıdır.

eşlenik gradyan

Eşlenik gradyan yöntemi, gradyan inişi ile Newton'un yöntemi arasında yer alır. Bu bir ara algoritmadır - gradyan iniş yönteminin yavaş yakınsama faktörünü hızlandırmayı amaçlarken, aynı zamanda Newton'un yönteminde genellikle gerekli olan Hessian matrisinin değerlendirilmesi, depolanması ve tersine çevrilmesi ile ilgili bilgi gereksinimlerine olan ihtiyacı ortadan kaldırır.

Eşlenik gradyan eğitim algoritması, gradyan iniş yönlerinden daha hızlı yakınsama sağlayan eşlenik yönlerde arama gerçekleştirir. Bu eğitim yönergeleri Hessian matrisine göre konjuge edilir. Burada d, eğitim yönü vektörünü gösterir. Bir başlangıç ​​parametre vektörü [w(0)] ve bir başlangıç ​​eğitim yönü vektörü [d(0)=−g(0)] ile başlarsak , eşlenik gradyan yöntemi şu şekilde temsil edilen bir eğitim yönleri dizisi oluşturur:

d(i+1) = g(i+1)+d(i)⋅γ(i),

Burada i = 0,1 ,… ve γ eşlenik parametredir. Tüm eşlenik gradyan algoritmaları için eğitim yönü , periyodik olarak gradyanın negatifine sıfırlanır. Parametreler iyileştirilir ve eğitim hızı ( η ), aşağıda gösterilen ifadeye göre çizgi minimizasyonu yoluyla elde edilir:

w(i+1) = w(i)+d(i)⋅η(i)

Burada, i = 0,1 ,…

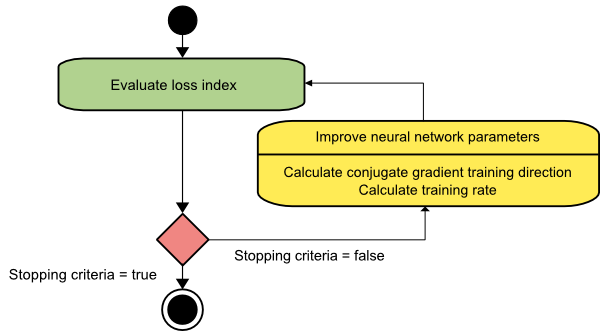
Kaynak

Çözüm

Her algoritma benzersiz avantajlar ve dezavantajlarla birlikte gelir. Bunlar, Sinir Ağlarını eğitmek için kullanılan yalnızca birkaç algoritmadır ve işlevleri buzdağının yalnızca görünen yüzünü gösterir - Derin Öğrenme çerçeveleri ilerledikçe, bu algoritmaların işlevleri de artacaktır.

Sinir ağı, makine öğrenimi programları ve AI hakkında daha fazla bilgi edinmek istiyorsanız, IIIT-B & upGrad'ın çalışan profesyoneller için tasarlanmış ve 450+ saatlik zorlu eğitim, 30+ vaka çalışmaları ve ödevler, IIIT-B Mezun statüsü, 5'ten fazla pratik uygulamalı bitirme projesi ve en iyi firmalarla iş yardımı.