Rețea neuronală: arhitectură, componente și algoritmi de top

Rețelele neuronale artificiale (ANN) fac parte integrantă din procesul de învățare profundă. Ele sunt inspirate de structura neurologică a creierului uman. Potrivit AILabPage , ANN-urile sunt „cod computerizat complex scris cu un număr de elemente de procesare simple, foarte interconectate, care este inspirat de structura creierului biologic uman pentru simularea modelelor de prelucrare și procesare a datelor (informații) ale creierului uman”.

Alăturați-vă online celor mai bune certificări de învățare automată de la cele mai bune universități din lume – masterat, programe executive postuniversitare și program de certificat avansat în ML și AI pentru a vă accelera cariera.

Deep Learning se concentrează pe cinci rețele neuronale de bază, inclusiv:

• Perceptron cu mai multe straturi
• Rețea de bază radială
• Rețele neuronale recurente
• Rețele adversare generative
• Rețele neuronale convoluționale.

Rețea neuronală: arhitectură

Rețelele neuronale sunt structuri complexe formate din neuroni artificiali care pot prelua mai multe intrări pentru a produce o singură ieșire. Aceasta este sarcina principală a unei rețele neuronale - de a transforma intrarea într-o ieșire semnificativă. De obicei, o rețea neuronală constă dintr-un strat de intrare și de ieșire cu unul sau mai multe straturi ascunse în interior.

Într-o rețea neuronală, toți neuronii se influențează reciproc și, prin urmare, toți sunt conectați. Rețeaua poate recunoaște și observa fiecare aspect al setului de date la îndemână și modul în care diferitele părți ale datelor se pot relaționa între ele sau nu. Acesta este modul în care rețelele neuronale sunt capabile să găsească tipare extrem de complexe în volume mari de date.

Citiți: Învățare automată vs rețele neuronale

Într-o rețea neuronală, fluxul de informații are loc în două moduri:

• Rețele Feedforward: În acest model, semnalele se deplasează doar într-o singură direcție, către stratul de ieșire. Rețelele Feedforward au un strat de intrare și un singur strat de ieșire cu zero sau mai multe straturi ascunse. Ele sunt utilizate pe scară largă în recunoașterea modelelor.
• Rețele de feedback: în acest model, rețelele recurente sau interactive își folosesc starea internă (memoria) pentru a procesa secvența de intrări. În ele, semnalele pot călători în ambele direcții prin buclele (stratul/erile ascunse) din rețea. Ele sunt de obicei utilizate în serii de timp și sarcini secvențiale.

Rețea neuronală: Componente

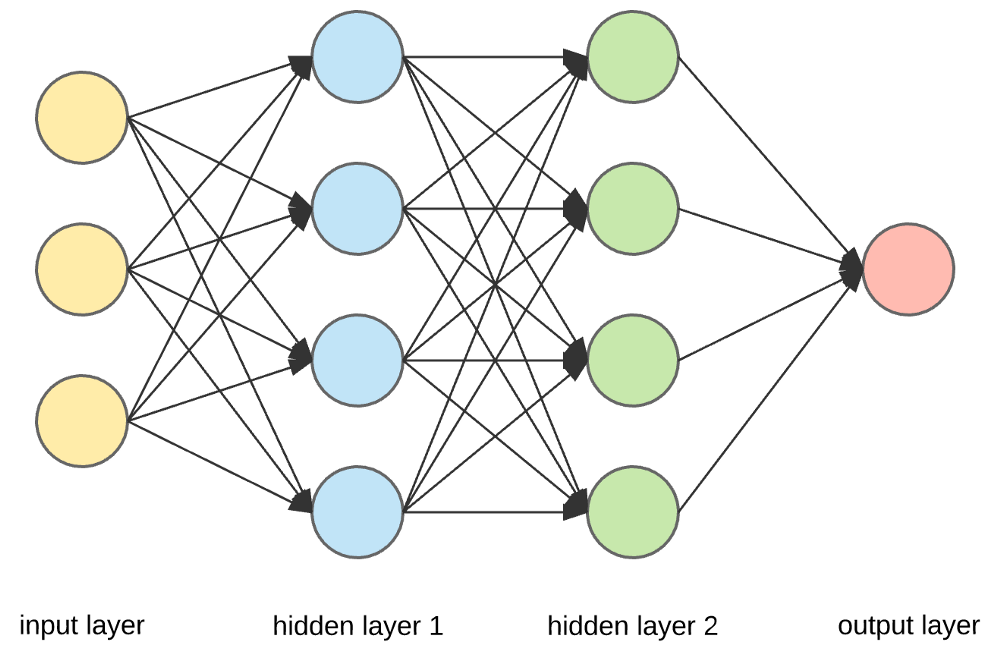
Sursă

Straturi de intrare, neuroni și greutăți –

În imaginea de mai sus, stratul galben cel mai exterior este stratul de intrare. Un neuron este unitatea de bază a unei rețele neuronale. Ei primesc intrare de la o sursă externă sau de la alte noduri. Fiecare nod este conectat cu un alt nod din stratul următor și fiecare astfel de conexiune are o anumită greutate. Greutățile sunt atribuite unui neuron pe baza importanței sale relative față de alte intrări.

Când toate valorile nodurilor din stratul galben sunt multiplicate (împreună cu greutatea lor) și rezumate, se generează o valoare pentru primul strat ascuns. Pe baza valorii rezumate, stratul albastru are o funcție de „activare” predefinită care determină dacă acest nod va fi sau nu „activat” și cât de „activ” va fi.

Să înțelegem acest lucru folosind o sarcină simplă de zi cu zi - prepararea ceaiului. În procesul de preparare a ceaiului, ingredientele folosite la prepararea ceaiului (apă, frunze de ceai, lapte, zahăr și condimente) sunt „neuronii”, deoarece alcătuiesc punctele de plecare ale procesului. Cantitatea fiecărui ingredient reprezintă „greutatea”. Odată ce pui frunzele de ceai în apă și adaugi zahărul, condimentele și laptele în tigaie, toate ingredientele se vor amesteca și se vor transforma într-o altă stare. Acest proces de transformare reprezintă „funcția de activare”.

Aflați despre: Deep Learning vs Neural Networks

Straturi ascunse și stratul de ieșire –

Stratul sau straturile ascunse între stratul de intrare și cel de ieșire sunt cunoscute sub denumirea de strat ascuns. Se numește stratul ascuns, deoarece este întotdeauna ascuns de lumea exterioară. Calculul principal al unei rețele neuronale are loc în straturile ascunse. Deci, stratul ascuns preia toate intrările din stratul de intrare și efectuează calculul necesar pentru a genera un rezultat. Acest rezultat este apoi transmis la stratul de ieșire, astfel încât utilizatorul să poată vizualiza rezultatul calculului.

În exemplul nostru de preparare a ceaiului, atunci când amestecăm toate ingredientele, formularea își schimbă starea și culoarea la încălzire. Ingredientele reprezintă straturile ascunse. Aici încălzirea reprezintă procesul de activare care oferă în cele din urmă rezultatul – ceaiul.

Rețeaua neuronală: algoritmi

Într-o rețea neuronală, procesul de învățare (sau de formare) este inițiat prin împărțirea datelor în trei seturi diferite:

• Set de date de antrenament – ​​Acest set de date permite rețelei neuronale să înțeleagă greutățile dintre noduri.
• Set de date de validare – Acest set de date este utilizat pentru reglarea fină a performanței rețelei neuronale.
• Set de date de testare – Acest set de date este utilizat pentru a determina acuratețea și marja de eroare a rețelei neuronale.

Odată ce datele sunt segmentate în aceste trei părți, li se aplică algoritmi de rețea neuronală pentru antrenarea rețelei neuronale. Procedura utilizată pentru facilitarea procesului de antrenament într-o rețea neuronală este cunoscută sub denumirea de optimizare, iar algoritmul utilizat se numește optimizator. Există diferite tipuri de algoritmi de optimizare, fiecare cu caracteristicile și aspectele lor unice, cum ar fi cerințele de memorie, precizia numerică și viteza de procesare.

Înainte de a aborda discuția despre diferiții algoritmi de rețea neuronală , să înțelegem mai întâi problema de învățare.

Citește și : Aplicații de rețele neuronale în lumea reală

Care este problema de învățare?

Reprezentăm problema învățării în termeni de minimizare a unui indice de pierdere ( f ). Aici, „ f ” este funcția care măsoară performanța unei rețele neuronale pe un anumit set de date. În general, indicele de pierdere constă dintr-un termen de eroare și un termen de regularizare. În timp ce termenul de eroare evaluează modul în care o rețea neuronală se potrivește unui set de date, termenul de regularizare ajută la prevenirea problemei de supraadaptare prin controlul complexității efective a rețelei neuronale.

Funcția de pierdere [ f(w ] depinde de parametrii adaptativi – ponderi și părtiniri – ai rețelei neuronale, acești parametri pot fi grupați într-un singur vector de greutate n-dimensional ( w ).

Iată o reprezentare grafică a funcției de pierdere:

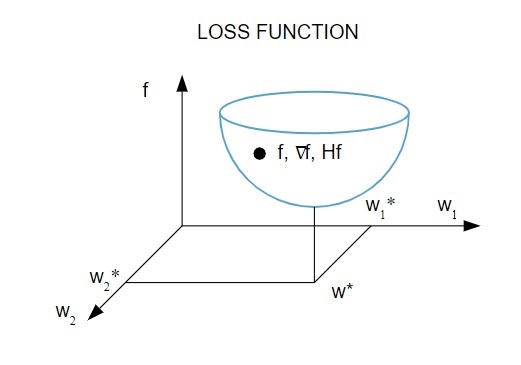
Sursă

Conform acestei diagrame, minimul funcției de pierdere are loc în punctul ( w* ). În orice moment, puteți calcula prima și a doua derivată a funcției de pierdere. Primele derivate sunt grupate în vectorul gradient, iar componentele sale sunt descrise ca:

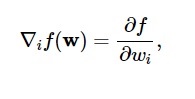
Sursă

Aici, i = 1,…..,n .

Derivatele secunde ale funcției de pierdere sunt grupate în matricea Hessiană , astfel:

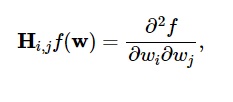
Sursă

Aici, i,j = 0,1,...

Acum că știm care este problema învățării, putem discuta cele cinci principale

Algoritmi de rețele neuronale .

1. Optimizare unidimensională

Deoarece funcția de pierdere depinde de mai mulți parametri, metodele de optimizare unidimensională sunt esențiale în formarea rețelei neuronale. Algoritmii de antrenament calculează mai întâi o direcție de antrenament ( d ) și apoi calculează rata de antrenament ( η ) care ajută la minimizarea pierderii în direcția de antrenament [ f(η) ].

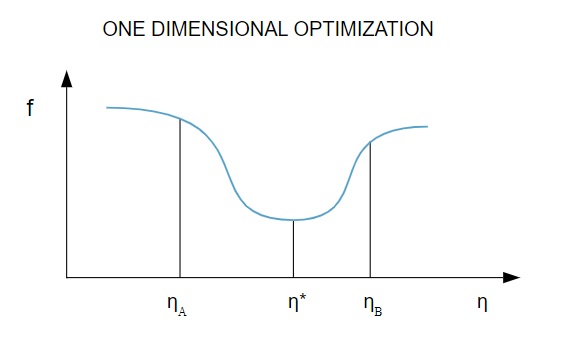
Sursă

În diagramă, punctele η1 și η2 definesc intervalul care conține minimul lui f, η* .

Astfel, metodele de optimizare unidimensională urmăresc găsirea minimului unei funcții unidimensionale date. Doi dintre cei mai des utilizați algoritmi unidimensionali sunt Metoda Secțiunii de Aur și Metoda lui Brent.

Metoda secțiunii de aur

Algoritmul de căutare a secțiunii de aur este utilizat pentru a găsi minimul sau maximul unei funcții cu o singură variabilă [ f(x) ]. Dacă știm deja că o funcție are un minim între două puncte, atunci putem efectua o căutare iterativă la fel cum am face-o în căutarea în bisecție pentru rădăcina unei ecuații f(x) = 0 . De asemenea, dacă putem găsi trei puncte ( x0 < x1 < x2 ) corespunzătoare lui f(x0) > f(x1) > f(X2) în vecinătatea minimului, atunci putem deduce că există un minim între x0 și x2 . Pentru a afla acest minim, putem lua în considerare un alt punct x3 între x1 și x2 , care ne va oferi următoarele rezultate:

• Dacă f(x3) = f3a > f(x1), minimul se află în interiorul intervalului x3 – x0 = a + c care este legat de trei puncte noi x0 < x1 < x3 (aici x2 este înlocuit cu x3 ).
• Dacă f(x3) = f3b > f(x1 ), minimul este în interiorul intervalului x2 – x1 = b legat de trei puncte noi x1 < x3 < x2 (aici x0 este înlocuit cu x1 ).

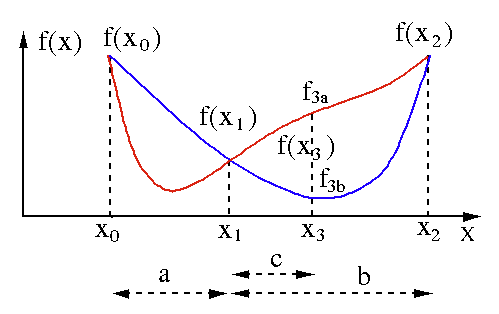
Sursă

Metoda lui Brent

Metoda lui Brent este un algoritm de găsire a rădăcinii care combină bracketingul rădăcinii , bisectia , secantele și interpolarea pătratică inversă . Deși acest algoritm încearcă să folosească metoda secantei cu convergență rapidă sau interpolarea pătratică inversă ori de câte ori este posibil, de obicei revine la metoda bisecției. Implementată în limbajul Wolfram , metoda lui Brent este exprimată astfel:

Metodă -> Brent în FindRoot [eqn, x, x0, x1].

În metoda lui Brent, folosim un polinom de interpolare Lagrange de gradul 2. În 1973, Brent a susținut că această metodă va converge întotdeauna, cu condiția ca valorile funcției să fie calculate într-o anumită regiune, inclusiv o rădăcină. Dacă există trei puncte x1, x2 și x3 , metoda lui Brent se potrivește cu x ca funcție pătratică a lui y , folosind formula de interpolare:

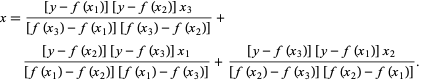
Sursă

Estimările ulterioare ale rădăcinii sunt realizate luând în considerare, producând astfel următoarea ecuație:

Sursă

Aici, P = S [ T(R – T) (x3 – x2) – (1 – R) (x2 -x1) ] și Q = (T – 1) (R – 1) (S – 1) și,

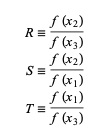
Sursă

2. Optimizare multidimensională

Până acum, știm deja că problema de învățare pentru rețelele neuronale își propune să găsească vectorul parametru ( w* ) pentru care funcția de pierdere ( f ) ia o valoare minimă. Conform mandatelor condiției standard, dacă rețeaua neuronală este la un nivel minim al funcției de pierdere, gradientul este vectorul zero.

Deoarece funcția de pierdere este o funcție neliniară a parametrilor, este imposibil să găsiți algoritmii de antrenament închis pentru minim. Totuși, dacă luăm în considerare căutarea prin spațiul parametrilor care include o serie de pași, la fiecare pas, pierderea se va reduce prin ajustarea parametrilor Rețelei Neurale.

În optimizarea multidimensională, o rețea neuronală este antrenată prin alegerea unui vector de parametri we aleatoriu și apoi generând o secvență de parametri pentru a se asigura că funcția de pierdere scade cu fiecare iterație a algoritmului. Această variație a pierderii între două etape ulterioare este cunoscută sub numele de „scăderea pierderii”. Procesul de scădere a pierderilor continuă până când algoritmul de antrenament atinge sau satisface condiția specificată.

Iată trei exemple de algoritmi de optimizare multidimensională:

Coborâre în gradient

Algoritmul de coborâre a gradientului este probabil cel mai simplu dintre toți algoritmii de antrenament. Deoarece se bazează pe informațiile furnizate din vectorul gradient, este o metodă de ordinul întâi. În această metodă, vom lua f[w(i)] = f(i) și ∇f[w(i)] = g(i) . Punctul de pornire al acestui algoritm de antrenament este w(0) care continuă să progreseze până când criteriul specificat este îndeplinit – se deplasează de la w(i) la w(i+1) în direcția de antrenament d(i) = −g(i) . Prin urmare, coborârea gradientului iterează după cum urmează:

w(i+1) = w(i)−g(i)η(i),

Aici, i = 0,1,...

Parametrul η reprezintă rata de antrenament. Puteți seta o valoare fixă ​​pentru η sau o puteți seta la valoarea găsită prin optimizarea unidimensională de-a lungul direcției de antrenament la fiecare pas. Cu toate acestea, se preferă să se stabilească valoarea optimă pentru rata de antrenament realizată prin minimizarea liniei la fiecare pas.

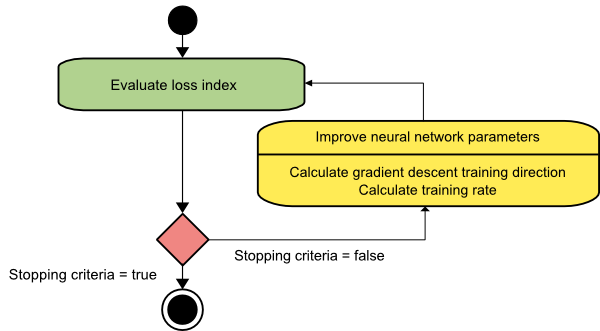
Sursă

Acest algoritm are multe limitări, deoarece necesită numeroase iterații pentru funcții care au structuri de vale lungi și înguste. În timp ce funcția de pierdere scade cel mai rapid în direcția gradientului în jos, nu asigură întotdeauna cea mai rapidă convergență.

metoda lui Newton

Acesta este un algoritm de ordinul doi, deoarece folosește matricea Hessiană. Metoda lui Newton urmărește să găsească direcții de antrenament mai bune prin utilizarea derivatelor secunde ale funcției de pierdere. Aici, vom nota f[w(i)] = f(i), ∇f[w(i)]=g(i) și Hf[w(i)] = H(i) . Acum, vom lua în considerare aproximarea pătratică a lui f la w(0) folosind expansiunea seriei lui Taylor, astfel:

f = f(0)+g(0)⋅[w−w(0)] + 0.5⋅[w−w(0)]2⋅H(0)

Aici, H(0) este matricea hessiană a lui f calculată în punctul w(0) . Considerând g = 0 pentru minimul lui f(w) , obținem următoarea ecuație:

g = g(0)+H(0)⋅(w−w(0))=0

Ca rezultat, putem observa că pornind de la vectorul parametru w(0), metoda lui Newton iterează după cum urmează:

w(i+1) = w(i)−H(i)−1⋅g(i)

Aici, i = 0,1 ,... iar vectorul H(i)−1⋅g(i) este denumit „pasul lui Newton”. Trebuie să rețineți că modificarea parametrului se poate deplasa către un maxim în loc să meargă în direcția unui minim. De obicei, acest lucru se întâmplă dacă matricea Hessiană nu este definită pozitiv, ceea ce face ca evaluarea funcției să fie redusă la fiecare iterație. Cu toate acestea, pentru a evita această problemă, de obicei modificăm ecuația metodei după cum urmează:

w(i+1) = w(i)−(H(i)−1⋅g(i))η

Aici, i = 0,1 ,….

Puteți fie seta rata de antrenament η la o valoare fixă, fie valoarea obținută prin minimizarea liniilor. Deci, vectorul d(i)=H(i)−1⋅g(i) devine direcția de antrenament pentru metoda lui Newton.

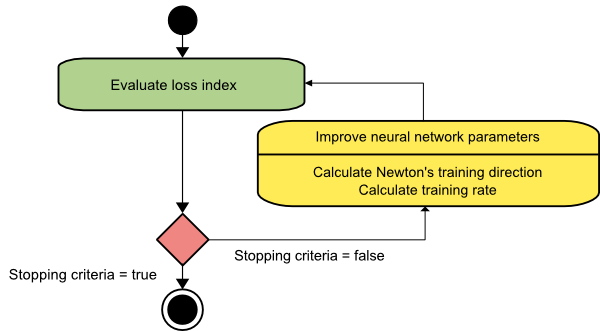
Sursă

Dezavantajul major al metodei lui Newton este că evaluarea exactă a Hessianului și inversul său sunt calcule destul de costisitoare.

Gradient conjugat

Metoda gradientului conjugat se încadrează între coborârea gradientului și metoda lui Newton. Este un algoritm intermediar – deși își propune să accelereze factorul de convergență lentă al metodei de coborâre a gradientului, elimină, de asemenea, nevoia de cerințe de informații referitoare la evaluarea, stocarea și inversarea matricei Hessian necesare de obicei în metoda lui Newton.

Algoritmul de antrenament al gradientului conjugat efectuează căutarea în direcțiile conjugate care oferă o convergență mai rapidă decât direcțiile de coborâre a gradientului. Aceste direcții de antrenament sunt conjugate în conformitate cu matricea Hessiană. Aici, d reprezintă vectorul direcției de antrenament. Dacă începem cu un vector parametru inițial [w(0)] și un vector de direcție inițială de antrenament [d(0)=−g(0)] , metoda gradientului conjugat generează o secvență de direcții de antrenament reprezentată ca:

d(i+1) = g(i+1)+d(i)⋅γ(i),

Aici, i = 0,1 ,... și γ este parametrul conjugat. Direcția de antrenament pentru toți algoritmii de gradient conjugați este resetată periodic la negativul gradientului. Parametrii sunt îmbunătățiți, iar rata de antrenament ( η ) este realizată prin minimizarea liniilor, conform expresiei prezentate mai jos:

w(i+1) = w(i)+d(i)⋅η(i)

Aici, i = 0,1 ,...

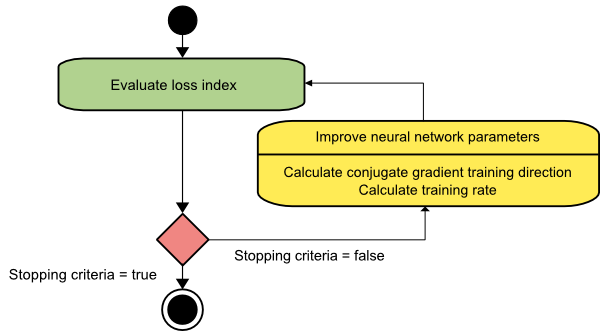
Sursă

Concluzie

Fiecare algoritm vine cu avantaje și dezavantaje unice. Aceștia sunt doar câțiva algoritmi folosiți pentru antrenarea rețelelor neuronale, iar funcțiile lor demonstrează doar vârful aisbergului – pe măsură ce cadrele de învățare profundă avansează, la fel și funcționalitățile acestor algoritmi.

Dacă sunteți interesat să aflați mai multe despre rețeaua neuronală, programele de învățare automată și AI , consultați Programul Executive PG de la IIIT-B și upGrad în Învățare automată și AI, care este conceput pentru profesioniști care lucrează și oferă peste 450 de ore de formare riguroasă, peste 30 studii de caz și sarcini, statutul de absolvenți IIIT-B, peste 5 proiecte practice practice și asistență pentru locuri de muncă cu firme de top.