神經網絡：架構、組件和頂級算法

人工神經網絡(ANN) 是深度學習過程中不可或缺的一部分。 它們的靈感來自人類大腦的神經結構。 根據AILabPage的說法，人工神經網絡是“由許多簡單、高度互連的處理元素編寫的複雜計算機代碼，其靈感來自人類生物大腦結構，用於模擬人腦工作和處理數據（信息）模型。”

在線加入來自世界頂級大學的最佳機器學習認證——機器學習和人工智能領域的碩士、高管研究生課程和高級證書課程，以加快您的職業生涯。

深度學習專注於五個核心神經網絡，包括：

• 多層感知器
• 徑向基網絡
• 遞歸神經網絡
• 生成對抗網絡
• 卷積神經網絡。

神經網絡：架構

神經網絡是由人工神經元組成的複雜結構，可以接收多個輸入以產生單個輸出。 這是神經網絡的主要工作——將輸入轉換為有意義的輸出。 通常，神經網絡由一個輸入和輸出層組成，其中包含一個或多個隱藏層。

在神經網絡中，所有的神經元都相互影響，因此它們都是相互連接的。 網絡可以確認和觀察手頭數據集的各個方面，以及數據的不同部分如何相互關聯或不相互關聯。 這就是神經網絡能夠在大量數據中找到極其複雜的模式的方式。

閱讀：機器學習與神經網絡

在神經網絡中，信息流以兩種方式發生——

• 前饋網絡：在此模型中，信號僅沿一個方向傳播，朝向輸出層。 前饋網絡有一個輸入層和一個帶有零個或多個隱藏層的輸出層。 它們廣泛用於模式識別。
• 反饋網絡：在這個模型中，循環或交互網絡使用它們的內部狀態（記憶）來處理輸入序列。 在它們中，信號可以通過網絡中的環路（隱藏層）雙向傳播。 它們通常用於時間序列和順序任務。

神經網絡：組件

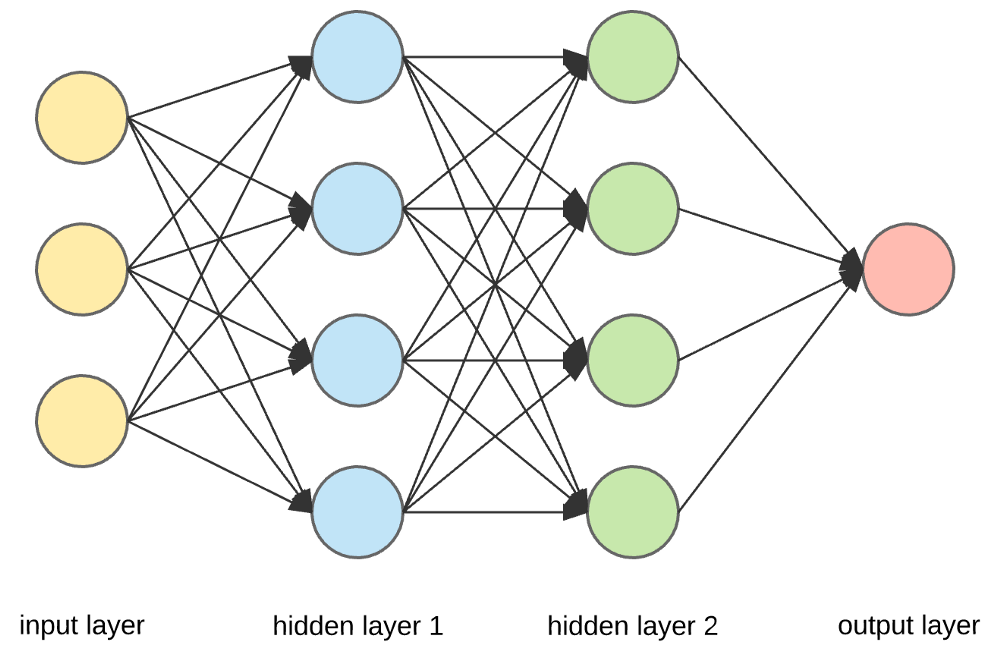
資源

輸入層、神經元和權重——

在上面給出的圖片中，最外面的黃色層是輸入層。 神經元是神經網絡的基本單元。 它們接收來自外部源或其他節點的輸入。 每個節點都與下一層的另一個節點相連，每個這樣的連接都有一個特定的權重。 根據神經元相對於其他輸入的相對重要性，將權重分配給神經元。

當黃色層的所有節點值相乘（連同它們的權重）並彙總時，它會為第一個隱藏層生成一個值。 基於匯總的值，藍色層有一個預定義的“激活”函數，它決定了這個節點是否會被“激活”以及它的“激活”程度。

讓我們通過一個簡單的日常任務來理解這一點——泡茶。 在製茶過程中，用於製茶的原料（水、茶葉、牛奶、糖和香料）是“神經元”，因為它們構成了過程的起點。 每種成分的量代表“重量”。 一旦你將茶葉放入水中，並在鍋中加入糖、香料和牛奶，所有成分都會混合併轉變為另一種狀態。 這個轉化過程代表了“激活功能”。

了解：深度學習與神經網絡

隱藏層和輸出層——

隱藏在輸入和輸出層之間的一層或多層稱為隱藏層。 它被稱為隱藏層，因為它總是對外部世界隱藏。 神經網絡的主要計算發生在隱藏層中。 因此，隱藏層從輸入層獲取所有輸入並執行必要的計算以生成結果。 然後將該結果轉發到輸出層，以便用戶查看計算結果。

在我們的製茶示例中，當我們混合所有成分時，配方會在加熱時改變其狀態和顏色。 成分代表隱藏層。 在這裡，加熱代表了最終產生結果的激活過程——茶。

神經網絡：算法

在神經網絡中，學習（或訓練）過程是通過將數據分成三個不同的集合來啟動的：

• 訓練數據集——該數據集允許神經網絡了解節點之間的權重。
• 驗證數據集——該數據集用於微調神​​經網絡的性能。
• 測試數據集——該數據集用於確定神經網絡的準確性和誤差範圍。

一旦數據被分割成這三個部分，神經網絡算法就會應用於它們以訓練神經網絡。 用於促進神經網絡中訓練過程的過程稱為優化，所使用的算法稱為優化器。 有不同類型的優化算法，每種算法都有其獨特的特徵和方面，例如內存要求、數值精度和處理速度。

在我們深入討論不同的神經網絡算法之前，讓我們先了解一下學習問題。

另請閱讀：現實世界中的神經網絡應用

什麼是學習問題？

我們根據損失指數( f )的最小化來表示學習問題。 這裡，“ f ”是衡量神經網絡在給定數據集上的性能的函數。 通常，損失指標由誤差項和正則化項組成。 雖然誤差項評估神經網絡如何擬合數據集，但正則化項通過控制神經網絡的有效複雜性來幫助防止過度擬合問題。

損失函數 [ f(w ] 取決於神經網絡的自適應參數——權重和偏差。這些參數可以分組為單個 n 維權重向量 ( w )。

這是損失函數的圖形表示：

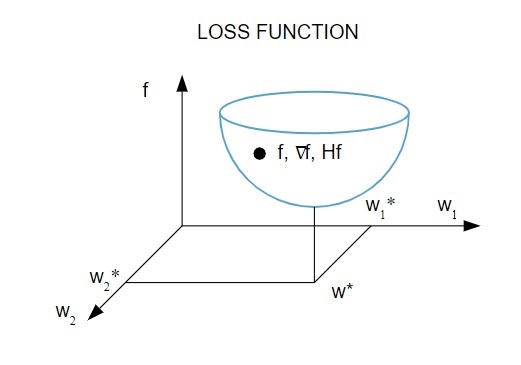
資源

根據該圖，損失函數的最小值出現在點 ( w* )。 在任何時候，您都可以計算損失函數的一階和二階導數。 一階導數在梯度向量中分組，其分量表示為：

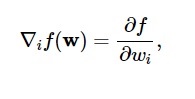
資源

在這裡， i = 1,…..,n 。

損失函數的二階導數在Hessian 矩陣中分組，如下所示：

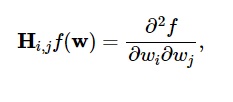
資源

這裡， i,j = 0,1,…

現在我們知道了學習問題是什麼，我們可以討論五個主要問題

神經網絡算法。

1.一維優化

由於損失函數取決於多個參數，因此一維優化方法有助於訓練神經網絡。 訓練算法首先計算訓練方向 ( d )，然後計算有助於最小化訓練方向損失的訓練率 ( η ) [ f(η) ]。

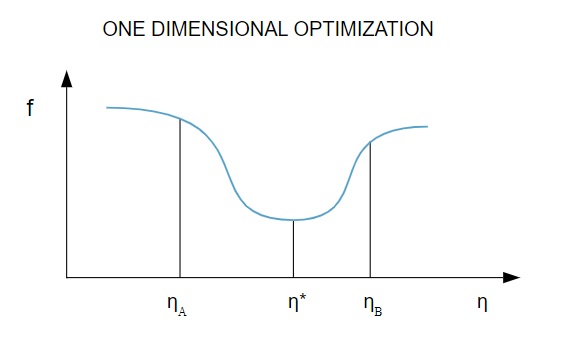
資源

在圖中，點 η1 和 η2 定義了包含f 的最小值 η*的區間。

因此，一維優化方法旨在找到給定一維函數的最小值。 最常用的兩種一維算法是黃金分割法和布倫特法。

黃金分割法

黃金分割搜索算法用於查找單變量函數 [ f(x) ] 的最小值或最大值。 如果我們已經知道函數在兩點之間具有最小值，那麼我們可以執行迭代搜索，就像我們在對等式f(x) = 0的根的二等分搜索中所做的那樣。 另外，如果我們可以在最小值的鄰域找到對應於f(x0) > f(x1) > f(X2)的三個點 ( x0 < x1 < x2 ) ，那麼我們可以推斷出x0和x2之間存在一個最小值. 為了找出這個最小值，我們可以考慮x1和x2之間的另一個點x3 ，這將給我們以下結果：

• 如果f(x3) = f3a > f(x1)，最小值在與三個新點x0 < x1 < x3相關的區間x3 – x0 = a + c內（這裡x2被x3替換）。
• 如果f(x3) = f3b > f(x1 )，最小值在區間x2 – x1 = b內，與三個新點x1 < x3 < x2相關（這裡x0被x1替換）。

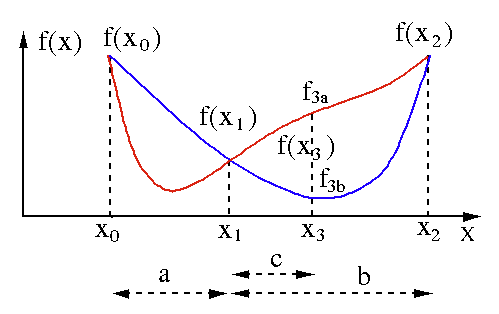
資源

布倫特方法

Brent 方法是一種求根算法，它結合了根包圍、二等分、割線和反二次插值。 儘管該算法盡可能嘗試使用快速收斂割線法或反二次插值法，但它通常會恢復為二等分法。 在Wolfram 語言中實現的 Brent 方法表示為：

方法 -> FindRoot [eqn, x, x0, x1] 中的 Brent。

在 Brent 的方法中，我們使用2 次拉格朗日插值多項式。1973年，Brent 聲稱該方法將始終收斂，前提是函數的值在特定區域內是可計算的，包括根。 如果存在三個點x1、x2和x3 ，則 Brent 方法使用插值公式將x擬合為y的二次函數：

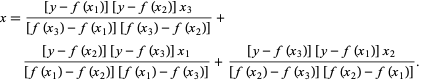
資源

隨後的根估計是通過考慮來實現的，從而產生以下等式：

資源

這裡， P = S [ T(R – T) (x3 – x2) – (1 – R) (x2 -x1) ]和Q = (T – 1) (R – 1) (S – 1) 並且，

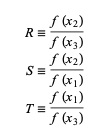
資源

2.多維優化

到目前為止，我們已經知道神經網絡的學習問題旨在找到損失函數 ( f ) 取最小值的參數向量 ( w* )。 根據標準條件的要求，如果神經網絡處於損失函數的最小值，則梯度為零向量。

由於損失函數是參數的非線性函數，因此不可能找到最小值的封閉訓練算法。 但是，如果我們考慮在包含一系列步驟的參數空間中進行搜索，則在每一步中，通過調整神經網絡的參數，損失都會減少。

在多維優化中，通過選擇一個隨機參數向量然後生成一系列參數來訓練神經網絡，以確保損失函數隨著算法的每次迭代而減小。 兩個後續步驟之間的這種損失變化稱為“損失遞減”。 損失遞減過程一直持續到訓練算法達到或滿足指定條件。

以下是多維優化算法的三個示例：

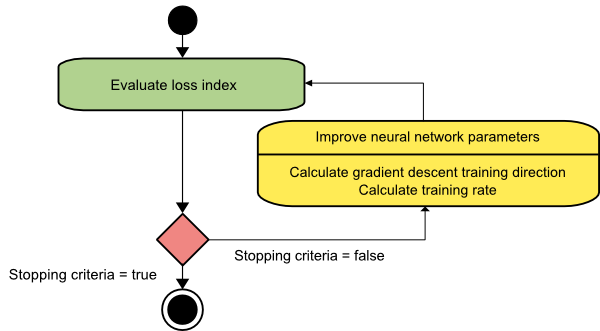
梯度下降

梯度下降算法可能是所有訓練算法中最簡單的。 因為它依賴於梯度向量提供的信息，所以它是一階方法。 在這種方法中，我們將採用f[w(i)] = f(i)和∇f[w(i)] = g(i) 。 該訓練算法的起點是 w(0)，它會一直進行直到滿足指定的標準——它在訓練方向上從 w(i) 移動到 w(i+1) d(i) = -g(i) . 因此，梯度下降迭代如下：

w(i+1) = w(i)-g(i)η(i),

在這裡，我 = 0,1，…

參數η表示訓練率。 您可以為η設置一個固定值或將其設置為在每一步沿訓練方向進行一維優化找到的值。 但是，最好為每一步通過線最小化實現的訓練率設置最佳值。

資源

該算法有許多限制，因為它需要對具有長而窄的谷結構的函數進行多次迭代。 雖然損失函數在下坡梯度方向下降得最快，但它並不總是確保最快的收斂。

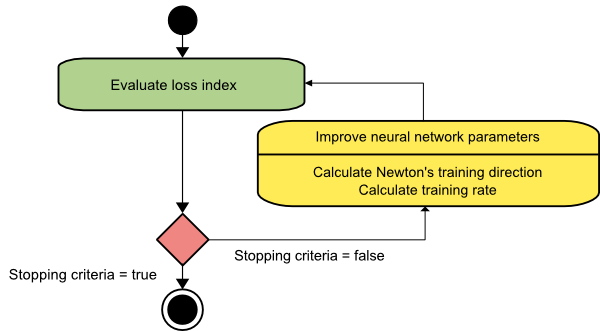
牛頓法

這是一個二階算法，因為它利用了 Hessian 矩陣。 牛頓的方法旨在通過利用損失函數的二階導數找到更好的訓練方向。 在這裡，我們將表示f[w(i)] = f(i)、∇f[w(i)]=g(i)和Hf[w(i)] = H(i) 。 現在，我們將使用泰勒級數展開來考慮f在w(0)處的二次逼近，如下所示：

f = f(0)+g(0)⋅[w−w(0)] + 0.5⋅[w−w(0)]2⋅H(0)

這裡， H(0)是在點w(0)處計算的f的 Hessian 矩陣。 通過考慮g = 0的最小值f(w) ，我們得到以下等式：

g = g(0)+H(0)⋅(w−w(0))=0

結果，我們可以看到，從參數向量w(0)開始，牛頓的方法迭代如下：

w(i+1) = w(i)−H(i)−1⋅g(i)

這裡， i = 0,1 ,… 並且向量H(i)−1⋅g(i)被稱為“牛頓步長”。 您必須記住，參數變化可能會向最大值移動，而不是向最小值方向移動。 通常，如果 Hessian 矩陣不是正定的，就會發生這種情況，從而導致函數評估在每次迭代時減少。 但是，為了避免這個問題，我們通常將方法方程修改如下：

w(i+1) = w(i)−(H(i)−1⋅g(i))η

在這裡，我 = 0,1 ,...。

您可以將訓練率 η 設置為固定值或通過線最小化獲得的值。 因此，向量d(i)=H(i)−1⋅g(i)成為牛頓法的訓練方向。

資源

牛頓方法的主要缺點是 Hessian 及其逆的精確計算是相當昂貴的計算。

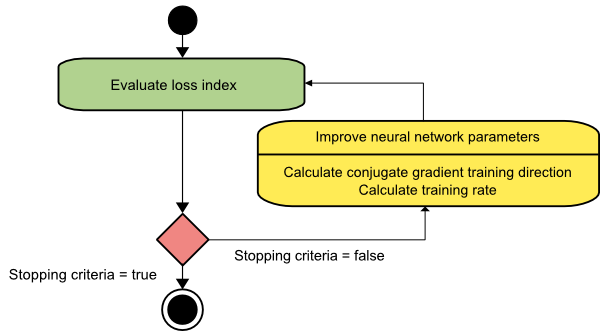
共軛梯度

共軛梯度法介於梯度下降法和牛頓法之間。 它是一種中間算法——雖然它旨在加速梯度下降法的緩慢收斂因子，但它也消除了牛頓法中通常需要的有關 Hessian 矩陣的評估、存儲和求逆的信息需求。

共軛梯度訓練算法在共軛方向上執行搜索，比梯度下降方向提供更快的收斂。 這些訓練方向是根據 Hessian 矩陣共軛的。 這裡，d 表示訓練方向向量。 如果我們從一個初始參數向量 [w(0)] 和一個初始訓練方向向量[d(0)=−g(0)]開始，共軛梯度方法會生成一個訓練方向序列，表示為：

d(i+1) = g(i+1)+d(i)⋅γ(i),

這裡， i = 0,1 ,… 和 γ 是共軛參數。 所有共軛梯度算法的訓練方向都會定期重置為梯度的負值。 參數得到改進，訓練率（ η ）通過線最小化來實現，根據如下所示的表達式：

w(i+1) = w(i)+d(i)⋅η(i)

在這裡，我 = 0,1 ，...

資源

結論

每種算法都有獨特的優點和缺點。 這些只是用於訓練神經網絡的少數算法，它們的功能只展示了冰山一角——隨著深度學習框架的進步，這些算法的功能也會隨之進步。

如果您有興趣了解有關神經網絡、機器學習程序和 AI的更多信息，請查看 IIIT-B 和 upGrad 的機器學習和 AI 執行 PG 計劃，該計劃專為工作專業人士設計，提供 450 多個小時的嚴格培訓，30 多個案例研究和作業、IIIT-B 校友身份、5 個以上實用的實踐頂點項目和頂級公司的工作協助。