Neural Network: Arsitektur, Komponen & Algoritma Teratas

Jaringan Syaraf Tiruan (JST) merupakan bagian integral dari proses Deep Learning. Mereka terinspirasi oleh struktur saraf otak manusia. Menurut AILabPage , JST adalah "kode komputer kompleks yang ditulis dengan sejumlah elemen pemrosesan sederhana yang sangat saling berhubungan yang terinspirasi oleh struktur otak biologis manusia untuk mensimulasikan model kerja & pemrosesan data (Informasi) otak manusia."

Bergabunglah dengan Sertifikasi Pembelajaran Mesin Terbaik online dari Universitas top dunia – Magister, Program Pascasarjana Eksekutif, dan Program Sertifikat Tingkat Lanjut di ML & AI untuk mempercepat karier Anda.

Deep Learning berfokus pada lima inti Neural Networks, termasuk:

• Perceptron Multi-Lapisan
• Jaringan Basis Radial
• Jaringan Saraf Berulang
• Jaringan Permusuhan Generatif
• Jaringan Saraf Konvolusi.

Jaringan Saraf: Arsitektur

Neural Network adalah struktur kompleks yang terbuat dari neuron buatan yang dapat menerima banyak input untuk menghasilkan satu output. Ini adalah tugas utama Neural Network – untuk mengubah input menjadi output yang berarti. Biasanya, Neural Network terdiri dari lapisan input dan output dengan satu atau beberapa lapisan tersembunyi di dalamnya.

Dalam Neural Network, semua neuron saling mempengaruhi, dan karenanya, mereka semua terhubung. Jaringan dapat mengenali dan mengamati setiap aspek dari kumpulan data yang ada dan bagaimana bagian-bagian data yang berbeda dapat saling berhubungan atau tidak. Beginilah cara Neural Networks mampu menemukan pola yang sangat kompleks dalam volume data yang sangat besar.

Baca: Pembelajaran Mesin vs Jaringan Neural

Dalam Neural Network, aliran informasi terjadi dalam dua cara –

• Feedforward Networks: Dalam model ini, sinyal hanya bergerak dalam satu arah, menuju lapisan output. Feedforward Networks memiliki lapisan input dan lapisan output tunggal dengan nol atau beberapa lapisan tersembunyi. Mereka banyak digunakan dalam pengenalan pola.
• Jaringan Umpan Balik: Dalam model ini, jaringan berulang atau interaktif menggunakan keadaan internal (memori) untuk memproses urutan input. Di dalamnya, sinyal dapat berjalan di kedua arah melalui loop (lapisan tersembunyi/s) di jaringan. Mereka biasanya digunakan dalam rangkaian waktu dan tugas berurutan.

Jaringan Saraf: Komponen

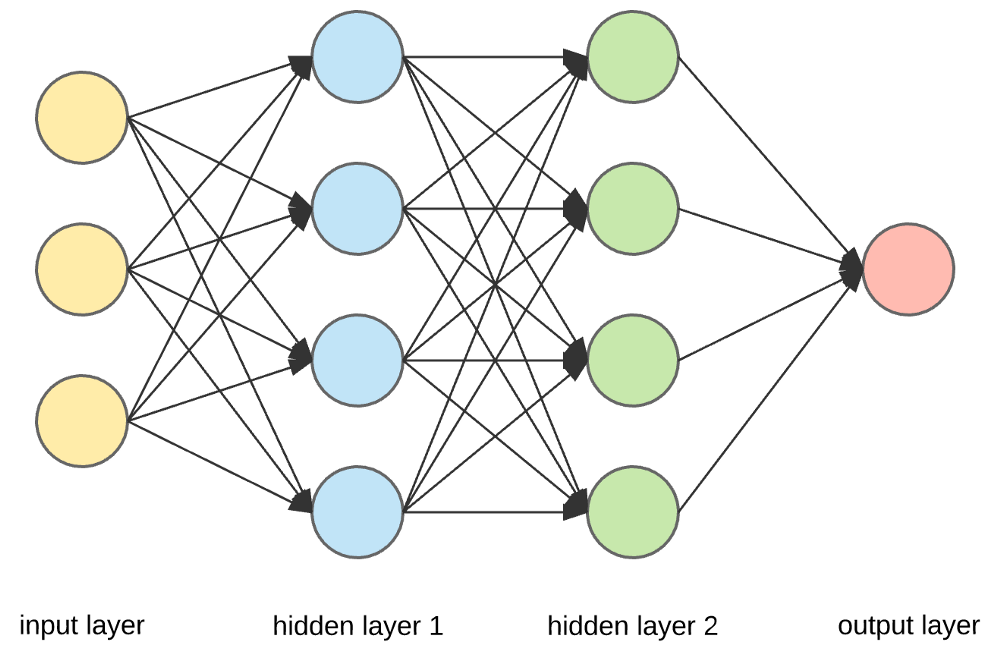
Sumber

Lapisan Input, Neuron, dan Bobot –

Pada gambar di atas, lapisan kuning terluar adalah lapisan input. Neuron adalah unit dasar dari jaringan saraf. Mereka menerima input dari sumber eksternal atau node lain. Setiap node terhubung dengan node lain dari lapisan berikutnya, dan setiap koneksi tersebut memiliki bobot tertentu. Bobot diberikan ke neuron berdasarkan kepentingan relatifnya terhadap input lainnya.

Ketika semua nilai simpul dari lapisan kuning dikalikan (bersama dengan bobotnya) dan diringkas, itu menghasilkan nilai untuk lapisan tersembunyi pertama. Berdasarkan nilai yang diringkas, lapisan biru memiliki fungsi "aktivasi" yang telah ditentukan sebelumnya yang menentukan apakah node ini akan "diaktifkan" dan seberapa "aktif" itu.

Mari kita pahami ini menggunakan tugas sehari-hari yang sederhana – membuat teh. Dalam proses pembuatan teh, bahan-bahan yang digunakan untuk membuat teh (air, daun teh, susu, gula, dan rempah-rempah) merupakan “neuron” karena merupakan titik awal proses. Jumlah masing-masing bahan mewakili "berat". Setelah Anda memasukkan daun teh ke dalam air dan menambahkan gula, bumbu, dan susu ke dalam panci, semua bahan akan bercampur dan berubah menjadi keadaan lain. Proses transformasi ini mewakili "fungsi aktivasi."

Pelajari tentang: Deep Learning vs Neural Networks

Lapisan Tersembunyi dan Lapisan Keluaran –

Lapisan atau lapisan yang tersembunyi di antara lapisan input dan output dikenal sebagai lapisan tersembunyi. Disebut lapisan tersembunyi karena selalu tersembunyi dari dunia luar. Perhitungan utama Neural Network terjadi di lapisan tersembunyi. Jadi, lapisan tersembunyi mengambil semua input dari lapisan input dan melakukan perhitungan yang diperlukan untuk menghasilkan hasil. Hasil ini kemudian diteruskan ke output layer sehingga pengguna dapat melihat hasil komputasinya.

Dalam contoh pembuatan teh kami, saat kami mencampur semua bahan, formulasinya berubah bentuk dan warnanya saat dipanaskan. Bahan-bahannya mewakili lapisan tersembunyi. Di sini pemanasan mewakili proses aktivasi yang akhirnya memberikan hasil – teh.

Jaringan Saraf: Algoritma

Dalam Neural Network, proses pembelajaran (atau pelatihan) dimulai dengan membagi data menjadi tiga set yang berbeda:

• Dataset pelatihan – Dataset ini memungkinkan Neural Network untuk memahami bobot antar node.
• Validasi dataset – Dataset ini digunakan untuk menyempurnakan kinerja Neural Network.
• Test dataset – Dataset ini digunakan untuk menentukan akurasi dan margin of error Neural Network.

Setelah data tersegmentasi ke dalam tiga bagian ini, algoritma Neural Network diterapkan pada mereka untuk melatih Neural Network. Prosedur yang digunakan untuk memfasilitasi proses pelatihan di Neural Network dikenal sebagai optimasi, dan algoritma yang digunakan disebut optimasi. Ada berbagai jenis algoritme pengoptimalan, masing-masing dengan karakteristik dan aspek uniknya seperti persyaratan memori, presisi numerik, dan kecepatan pemrosesan.

Sebelum kita masuk ke pembahasan tentang algoritma Neural Network yang berbeda, mari kita pahami masalah pembelajarannya terlebih dahulu.

Baca juga : Aplikasi Neural Network di Dunia Nyata

Apa Masalah Pembelajaran?

Kami mewakili masalah pembelajaran dalam hal minimalisasi indeks kerugian ( f ). Di sini, “ f ” adalah fungsi yang mengukur kinerja Neural Network pada kumpulan data yang diberikan. Umumnya, indeks kerugian terdiri dari istilah kesalahan dan istilah regularisasi. Sementara istilah kesalahan mengevaluasi bagaimana Neural Network cocok dengan dataset, istilah regularisasi membantu mencegah masalah overfitting dengan mengendalikan kompleksitas efektif Neural Network.

Fungsi kerugian [ f(w ] tergantung pada parameter adaptif – bobot dan bias – dari Neural Network. Parameter ini dapat dikelompokkan ke dalam satu vektor bobot n-dimensi ( w ).

Berikut adalah representasi bergambar dari fungsi kerugian:

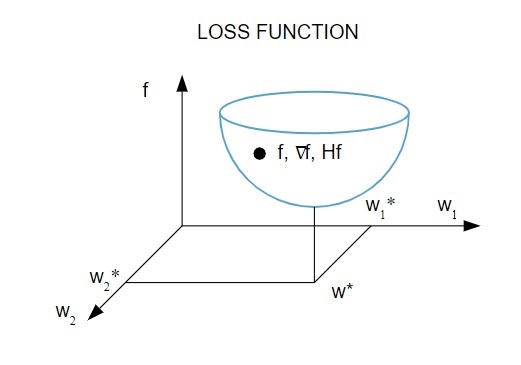
Sumber

Menurut diagram ini, fungsi kerugian minimum terjadi pada titik ( w* ). Kapan saja, Anda dapat menghitung turunan pertama dan kedua dari fungsi kerugian. Turunan pertama dikelompokkan dalam vektor gradien, dan komponennya digambarkan sebagai:

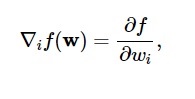
Sumber

Di sini, i = 1,…..,n .

Turunan kedua dari fungsi kerugian dikelompokkan dalam matriks Hessian , seperti:

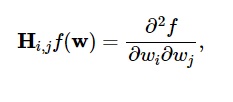
Sumber

Di sini, i,j = 0,1,…

Sekarang kita tahu apa masalah belajar, kita bisa membahas lima utama

Algoritma Neural Network .

1. Optimasi satu dimensi

Karena fungsi kerugian bergantung pada beberapa parameter, metode optimasi satu dimensi berperan penting dalam melatih Jaringan Saraf Tiruan. Algoritme pelatihan pertama-tama menghitung arah pelatihan ( d ) dan kemudian menghitung laju pelatihan ( ) yang membantu meminimalkan kerugian dalam arah pelatihan [ f(η) ] .

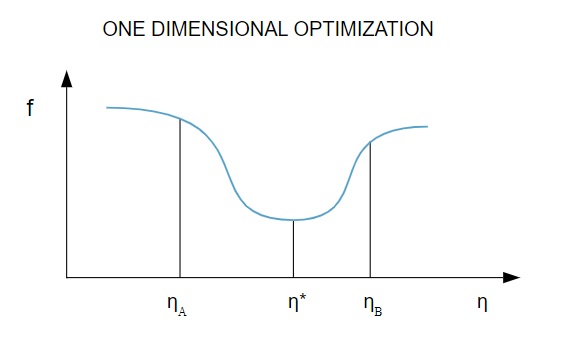
Sumber

Dalam diagram, titik 1 dan 2 mendefinisikan interval yang mengandung f, * minimum .

Dengan demikian, metode optimasi satu dimensi bertujuan untuk menemukan minimum dari fungsi satu dimensi yang diberikan. Dua dari algoritma satu dimensi yang paling umum digunakan adalah Metode Bagian Emas dan Metode Brent.

Metode Bagian Emas

Algoritma pencarian bagian emas digunakan untuk menemukan minimum atau maksimum dari fungsi variabel tunggal [ f(x) ]. Jika kita telah mengetahui bahwa suatu fungsi memiliki minimum antara dua titik, maka kita dapat melakukan pencarian iteratif seperti yang kita lakukan pada pencarian bagi dua akar persamaan f(x) = 0 . Juga, jika kita dapat menemukan tiga titik ( x0 < x1 < x2 ) yang sesuai dengan f(x0) > f(x1) > f(X2) di lingkungan minimum, maka kita dapat menyimpulkan bahwa minimum ada antara x0 dan x2 . Untuk mengetahui minimum ini, kita dapat mempertimbangkan titik lain x3 antara x1 dan x2 , yang akan memberi kita hasil berikut:

• Jika f(x3) = f3a > f(x1), nilai minimum berada di dalam interval x3 – x0 = a + c yang berhubungan dengan tiga titik baru x0 < x1 < x3 (di sini x2 diganti dengan x3 ).
• Jika f(x3) = f3b > f(x1 ), minimum berada di dalam interval x2 – x1 = b terkait dengan tiga titik baru x1 < x3 < x2 (di sini x0 diganti dengan x1 ).

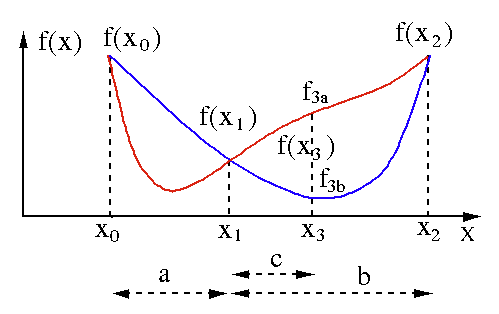
Sumber

Metode Brent

Metode Brent adalah algoritma pencarian akar yang menggabungkan root bracketing , bisection , secant , dan inverse quadratic interpolation . Meskipun algoritma ini mencoba menggunakan metode garis potong cepat konvergen atau interpolasi kuadrat terbalik bila memungkinkan, biasanya kembali ke metode bagi dua. Diimplementasikan dalam Bahasa Wolfram , metode Brent dinyatakan sebagai:

Metode -> Brent di FindRoot [eqn, x, x0, x1].

Dalam metode Brent, kami menggunakan polinomial interpolasi Lagrange derajat 2. Pada tahun 1973, Brent mengklaim bahwa metode ini akan selalu konvergen, asalkan nilai fungsi dapat dihitung dalam wilayah tertentu, termasuk akar. Jika ada tiga titik x1, x2, dan x3 , Metode Brent cocok x sebagai fungsi kuadrat dari y , menggunakan rumus interpolasi:

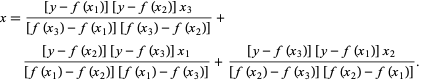
Sumber

Estimasi akar berikutnya dicapai dengan mempertimbangkan, sehingga menghasilkan persamaan berikut:

Sumber

Di sini, P = S [ T(R – T) (x3 – x2) – (1 – R) (x2 -x1) ] dan Q = (T – 1) (R – 1) (S – 1) dan,

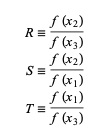
Sumber

2. Optimalisasi multidimensi

Sekarang, kita telah mengetahui bahwa masalah pembelajaran Jaringan Syaraf Tiruan bertujuan untuk menemukan vektor parameter ( w* ) dimana fungsi kerugian ( f ) mengambil nilai minimum. Sesuai dengan mandat kondisi standar, jika Neural Network berada pada fungsi loss minimum, gradiennya adalah vektor nol.

Karena fungsi kerugian adalah fungsi non-linier dari parameter, tidak mungkin untuk menemukan algoritma pelatihan tertutup untuk minimum. Namun, jika kita mempertimbangkan pencarian melalui ruang parameter yang mencakup serangkaian langkah, pada setiap langkah, kerugian akan berkurang dengan menyesuaikan parameter Jaringan Saraf Tiruan.

Dalam optimasi multidimensi, Neural Network dilatih dengan memilih vektor parameter kita secara acak dan kemudian menghasilkan urutan parameter untuk memastikan bahwa fungsi kerugian berkurang dengan setiap iterasi algoritma. Variasi kerugian antara dua langkah berikutnya ini dikenal sebagai “pengurangan kerugian.” Proses pengurangan kerugian berlanjut sampai algoritma pelatihan mencapai atau memenuhi kondisi yang ditentukan.

Berikut adalah tiga contoh algoritma optimasi multidimensi:

Keturunan gradien

Algoritma penurunan gradien mungkin yang paling sederhana dari semua algoritma pelatihan. Karena bergantung pada informasi yang diberikan `dari vektor gradien, ini adalah metode orde pertama. Dalam metode ini, kita akan mengambil f[w(i)] = f(i) dan f[w(i)] = g(i) . Titik awal dari algoritma pelatihan ini adalah w(0) yang terus maju sampai kriteria yang ditentukan terpenuhi – ia bergerak dari w(i) ke w(i+1) dalam arah pelatihan d(i) = g(i) . Oleh karena itu, penurunan gradien berulang sebagai berikut:

w(i+1) = w(i)−g(i)η(i),

Di sini, saya = 0,1,…

Parameter mewakili tingkat pelatihan. Anda dapat menetapkan nilai tetap untuk atau menyetelnya ke nilai yang ditemukan oleh optimasi satu dimensi di sepanjang arah pelatihan di setiap langkah. Namun, lebih disukai untuk menetapkan nilai optimal untuk tingkat pelatihan yang dicapai dengan minimalisasi garis pada setiap langkah.

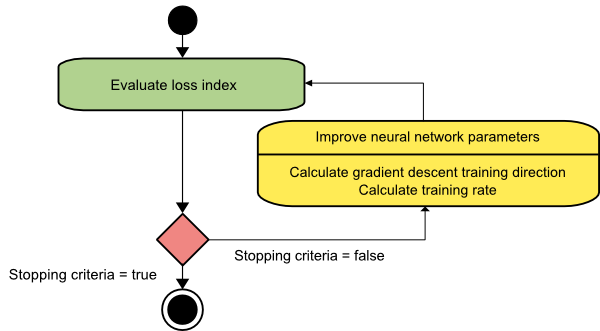
Sumber

Algoritma ini memiliki banyak keterbatasan karena memerlukan banyak iterasi untuk fungsi yang memiliki struktur lembah yang panjang dan sempit. Sementara fungsi kerugian menurun paling cepat ke arah gradien menurun, itu tidak selalu memastikan konvergensi tercepat.

metode Newton

Ini adalah algoritma orde kedua karena memanfaatkan matriks Hessian. Metode Newton bertujuan untuk menemukan arah pelatihan yang lebih baik dengan memanfaatkan turunan kedua dari fungsi kerugian. Di sini, kita akan menyatakan f[w(i)] = f(i), f[w(i)]=g(i) , dan Hf[w(i)] = H(i) . Sekarang, kita akan mempertimbangkan aproksimasi kuadrat dari f pada w(0) menggunakan ekspansi deret Taylor, seperti:

f = f(0)+g(0)⋅[w−w(0)] + 0,5⋅[w−w(0)]2⋅H(0)

Di sini, H(0) adalah matriks Hessian dari f yang dihitung pada titik w(0) . Dengan mempertimbangkan g = 0 untuk f(w) minimum , kita mendapatkan persamaan berikut:

g = g(0)+H(0)⋅(w−w(0))=0

Hasilnya, kita dapat melihat bahwa mulai dari vektor parameter w(0), metode Newton iterasi sebagai berikut:

w(i+1) = w(i)−H(i)−1⋅g(i)

Di sini, i = 0,1 ,… dan vektor H(i)−1⋅g(i) disebut sebagai “Langkah Newton”. Anda harus ingat bahwa perubahan parameter dapat bergerak ke arah maksimum, bukan ke arah minimum. Biasanya hal ini terjadi jika matriks Hessian tidak pasti positif, sehingga menyebabkan evaluasi fungsi berkurang pada setiap iterasi. Namun, untuk menghindari masalah ini, kami biasanya memodifikasi persamaan metode sebagai berikut:

w(i+1) = w(i)−(H(i)−1⋅g(i))η

Di sini, i = 0,1 ,….

Anda dapat mengatur tingkat pelatihan ke nilai tetap atau nilai yang diperoleh melalui minimalisasi garis. Jadi, vektor d(i)=H(i)−1⋅g(i) menjadi arah latihan untuk metode Newton.

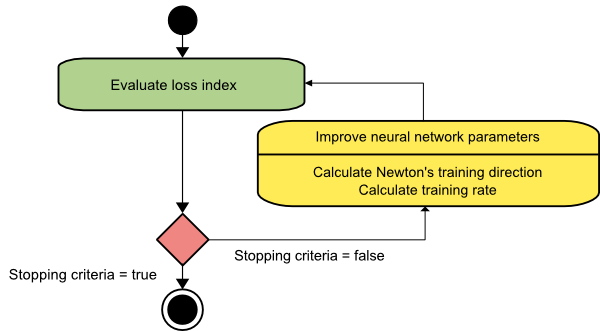
Sumber

Kelemahan utama dari metode Newton adalah bahwa evaluasi yang tepat dari Hessian dan kebalikannya adalah perhitungan yang cukup mahal.

Gradien konjugasi

Metode gradien konjugasi berada di antara penurunan gradien dan metode Newton. Ini adalah algoritma perantara - sementara itu bertujuan untuk mempercepat faktor konvergensi lambat dari metode penurunan gradien, itu juga menghilangkan kebutuhan untuk persyaratan informasi mengenai evaluasi, penyimpanan, dan inversi matriks Hessian biasanya diperlukan dalam metode Newton.

Algoritma pelatihan gradien konjugasi melakukan pencarian dalam arah konjugasi yang memberikan konvergensi lebih cepat daripada arah penurunan gradien. Arah pelatihan ini terkonjugasi sesuai dengan matriks Hessian. Di sini, d menunjukkan vektor arah pelatihan. Jika kita mulai dengan vektor parameter awal [w(0)] dan vektor arah pelatihan awal [d(0)=−g(0)] , metode gradien konjugasi menghasilkan urutan arah pelatihan yang direpresentasikan sebagai:

d(i+1) = g(i+1)+d(i)⋅γ(i),

Di sini, i = 0,1 ,… dan adalah parameter konjugasi. Arah pelatihan untuk semua algoritma gradien konjugasi secara berkala diatur ulang ke negatif gradien. Parameter ditingkatkan, dan tingkat pelatihan ( ) dicapai melalui minimalisasi garis, sesuai dengan ekspresi yang ditunjukkan di bawah ini:

w(i+1) = w(i)+d(i)⋅η(i)

Di sini, i = 0,1 ,…

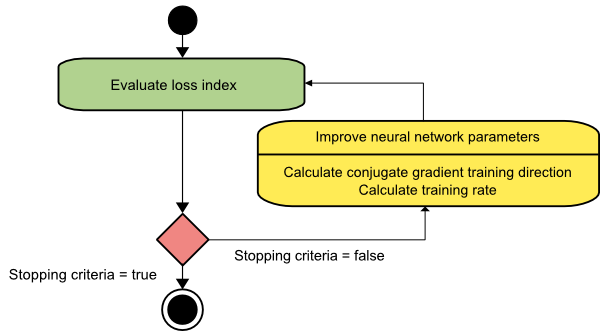
Sumber

Kesimpulan

Setiap algoritma hadir dengan kelebihan dan kekurangan yang unik. Ini hanya beberapa algoritme yang digunakan untuk melatih Neural Networks, dan fungsinya hanya menunjukkan puncak gunung es – seiring berkembangnya kerangka kerja Deep Learning , demikian pula fungsionalitas algoritme ini.

Jika Anda tertarik untuk mempelajari lebih lanjut tentang jaringan saraf, program pembelajaran mesin & AI , lihat Program PG Eksekutif IIIT-B & upGrad dalam Pembelajaran Mesin & AI yang dirancang untuk profesional yang bekerja dan menawarkan 450+ jam pelatihan yang ketat, 30+ studi kasus & tugas, status Alumni IIIT-B, 5+ proyek batu penjuru praktis & bantuan pekerjaan dengan perusahaan-perusahaan top.