الشبكة العصبية: العمارة والمكونات وأفضل الخوارزميات

تشكل الشبكات العصبية الاصطناعية (ANNs) جزءًا لا يتجزأ من عملية التعلم العميق. إنها مستوحاة من التركيب العصبي للدماغ البشري. وفقًا لـ AILabPage ، فإن الشبكات العصبية الاصطناعية هي "رمز كمبيوتر معقد مكتوب بعدد من عناصر المعالجة البسيطة والمترابطة للغاية والمستوحاة من بنية الدماغ البيولوجي البشري لمحاكاة نماذج البيانات (المعلومات) التي تعمل بالدماغ البشري."

انضم إلى أفضل شهادات التعلم الآلي عبر الإنترنت من أفضل الجامعات في العالم - الماجستير ، وبرامج الدراسات العليا التنفيذية ، وبرنامج الشهادات المتقدمة في ML & AI لتسريع حياتك المهنية.

يركز التعلم العميق على خمس شبكات عصبية أساسية ، بما في ذلك:

• متعدد الطبقات المستقبلات
• شبكة الأساس الشعاعي
• الشبكات العصبية المتكررة
• شبكات الخصومة التوليدية
• الشبكات العصبية التلافيفية.

الشبكة العصبية: العمارة

الشبكات العصبية هي هياكل معقدة مصنوعة من الخلايا العصبية الاصطناعية التي يمكن أن تأخذ مدخلات متعددة لإنتاج ناتج واحد. هذه هي الوظيفة الأساسية للشبكة العصبية - لتحويل المدخلات إلى مخرجات ذات مغزى. عادة ، تتكون الشبكة العصبية من طبقة إدخال وإخراج مع طبقة مخفية واحدة أو عدة طبقات مخفية بداخلها.

في الشبكة العصبية ، تؤثر جميع الخلايا العصبية على بعضها البعض ، وبالتالي فهي كلها متصلة ببعضها البعض. يمكن للشبكة أن تقر وتراقب كل جانب من جوانب مجموعة البيانات في متناول اليد وكيف يمكن أو لا ترتبط أجزاء مختلفة من البيانات ببعضها البعض. هذه هي الطريقة التي تستطيع بها الشبكات العصبية إيجاد أنماط معقدة للغاية في أحجام هائلة من البيانات.

قراءة: التعلم الآلي مقابل الشبكات العصبية

في الشبكة العصبية ، يحدث تدفق المعلومات بطريقتين -

• شبكات Feedforward: في هذا النموذج ، تنتقل الإشارات فقط في اتجاه واحد ، نحو طبقة الإخراج. تحتوي شبكات Feedforward على طبقة إدخال وطبقة إخراج واحدة مع صفر أو طبقات مخفية متعددة. تستخدم على نطاق واسع في التعرف على الأنماط.
• شبكات التغذية الراجعة: في هذا النموذج ، تستخدم الشبكات المتكررة أو التفاعلية حالتها الداخلية (الذاكرة) لمعالجة تسلسل المدخلات. في داخلها ، يمكن للإشارات أن تنتقل في كلا الاتجاهين عبر الحلقات (الطبقة / الطبقات المخفية) في الشبكة. يتم استخدامها عادةً في مهام متسلسلة زمنية ومتسلسلة.

الشبكة العصبية: مكونات

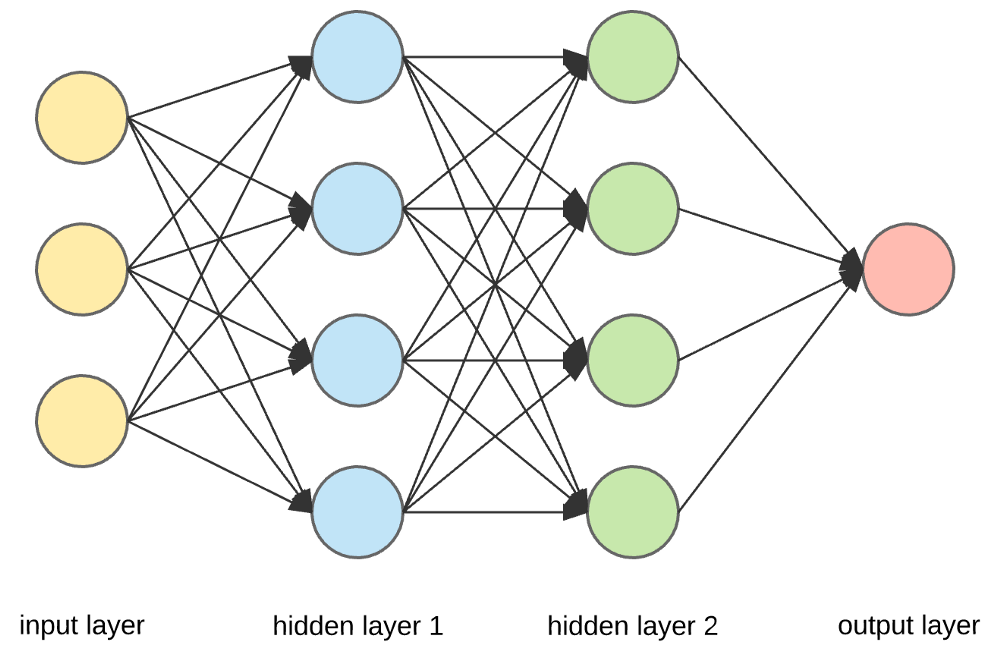
مصدر

طبقات الإدخال والخلايا العصبية والأوزان -

في الصورة أعلاه ، الطبقة الصفراء الخارجية هي طبقة الإدخال. الخلية العصبية هي الوحدة الأساسية للشبكة العصبية. يتلقون مدخلات من مصدر خارجي أو عقد أخرى. كل عقدة متصلة بعقدة أخرى من الطبقة التالية ، ولكل اتصال وزن معين. يتم تعيين أوزان للخلايا العصبية بناءً على أهميتها النسبية مقابل المدخلات الأخرى.

عندما يتم ضرب جميع قيم العقدة من الطبقة الصفراء (مع وزنها) وتلخيصها ، فإنها تولد قيمة للطبقة المخفية الأولى. استنادًا إلى القيمة المُلخصة ، تحتوي الطبقة الزرقاء على وظيفة "تنشيط" محددة مسبقًا تحدد ما إذا كانت هذه العقدة سيتم "تنشيطها" أم لا ومدى "نشاطها".

دعونا نفهم هذا باستخدام مهمة يومية بسيطة - صنع الشاي. في عملية صنع الشاي ، تعتبر المكونات المستخدمة لصنع الشاي (الماء وأوراق الشاي والحليب والسكر والتوابل) بمثابة "الخلايا العصبية" لأنها تشكل نقاط البداية للعملية. يمثل مقدار كل مكون "الوزن". بمجرد وضع أوراق الشاي في الماء وإضافة السكر والبهارات والحليب في المقلاة ، ستختلط جميع المكونات وتتحول إلى حالة أخرى. تمثل عملية التحول هذه "وظيفة التنشيط".

تعرف على المزيد حول: Deep Learning vs Neural Networks

الطبقات المخفية وطبقة الإخراج -

تُعرف الطبقة أو الطبقات المخفية بين طبقة الإدخال والإخراج بالطبقة المخفية. يطلق عليها الطبقة المخفية لأنها دائمًا ما تكون مخفية عن العالم الخارجي. يحدث الحساب الرئيسي للشبكة العصبية في الطبقات المخفية. لذلك ، تأخذ الطبقة المخفية جميع المدخلات من طبقة الإدخال وتقوم بالحسابات اللازمة لتوليد نتيجة. يتم إعادة توجيه هذه النتيجة بعد ذلك إلى طبقة الإخراج حتى يتمكن المستخدم من عرض نتيجة الحساب.

في مثالنا لصنع الشاي ، عندما نخلط جميع المكونات ، تغير التركيبة حالتها ولونها عند التسخين. المكونات تمثل الطبقات المخفية. يمثل التسخين هنا عملية التنشيط التي تحقق النتيجة أخيرًا - الشاي.

الشبكة العصبية: الخوارزميات

في الشبكة العصبية ، تبدأ عملية التعلم (أو التدريب) من خلال تقسيم البيانات إلى ثلاث مجموعات مختلفة:

• مجموعة بيانات التدريب - تسمح مجموعة البيانات هذه للشبكة العصبية بفهم الأوزان بين العقد.
• مجموعة بيانات التحقق - تُستخدم مجموعة البيانات هذه لضبط أداء الشبكة العصبية.
• مجموعة بيانات الاختبار - تُستخدم مجموعة البيانات هذه لتحديد دقة وهامش الخطأ في الشبكة العصبية.

بمجرد تقسيم البيانات إلى هذه الأجزاء الثلاثة ، يتم تطبيق خوارزميات الشبكة العصبية عليها لتدريب الشبكة العصبية. يُعرف الإجراء المستخدم لتسهيل عملية التدريب في الشبكة العصبية بالتحسين ، وتسمى الخوارزمية المستخدمة المحسن. هناك أنواع مختلفة من خوارزميات التحسين ، ولكل منها خصائصها وجوانبها الفريدة مثل متطلبات الذاكرة والدقة العددية وسرعة المعالجة.

قبل الغوص في مناقشة خوارزميات الشبكة العصبية المختلفة ، دعونا نفهم مشكلة التعلم أولاً.

اقرأ أيضًا : تطبيقات الشبكة العصبية في العالم الحقيقي

ما هي مشكلة التعلم؟

نحن نمثل مشكلة التعلم من حيث تقليل مؤشر الخسارة ( f ). هنا ، " f " هي الوظيفة التي تقيس أداء الشبكة العصبية في مجموعة بيانات معينة. بشكل عام ، يتكون مؤشر الخسارة من مصطلح خطأ ومصطلح تسوية. بينما يقيِّم مصطلح الخطأ كيفية ملاءمة الشبكة العصبية لمجموعة بيانات ، فإن مصطلح التنظيم يساعد في منع مشكلة فرط التخصيص من خلال التحكم في التعقيد الفعال للشبكة العصبية.

تعتمد وظيفة الخسارة [ f (w ] على المعلمات التكيفية - الأوزان والتحيزات - للشبكة العصبية ، ويمكن تجميع هذه المعلمات في متجه وزن أحادي البعد ( w ).

إليك تمثيل تصويري لوظيفة الخسارة:

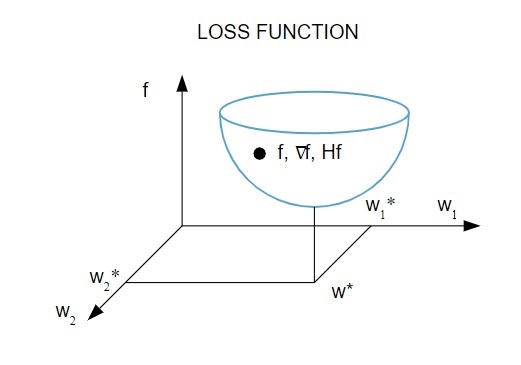
مصدر

وفقًا لهذا الرسم التخطيطي ، يحدث الحد الأدنى لوظيفة الخسارة عند النقطة ( w * ). في أي وقت ، يمكنك حساب المشتقات الأولى والثانية لوظيفة الخسارة. يتم تجميع المشتقات الأولى في متجه التدرج ، ويتم وصف مكوناتها على النحو التالي:

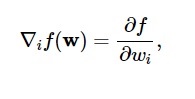
مصدر

هنا ، أنا = 1 ،… .. ، ن .

يتم تجميع المشتقات الثانية لوظيفة الخسارة في مصفوفة هسي ، على النحو التالي:

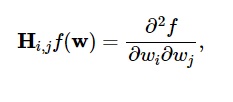
مصدر

هنا ، أنا ، ي = 0،1 ، ...

الآن بعد أن عرفنا ما هي مشكلة التعلم ، يمكننا مناقشة الخمسة الرئيسية

خوارزميات الشبكة العصبية .

1. التحسين أحادي البعد

نظرًا لأن وظيفة الخسارة تعتمد على معلمات متعددة ، فإن طرق التحسين أحادية البعد مفيدة في تدريب الشبكة العصبية. تقوم خوارزميات التدريب أولاً بحساب اتجاه التدريب ( د ) ثم حساب معدل التدريب ( η ) الذي يساعد على تقليل الخسارة في اتجاه التدريب [ f (η) ].

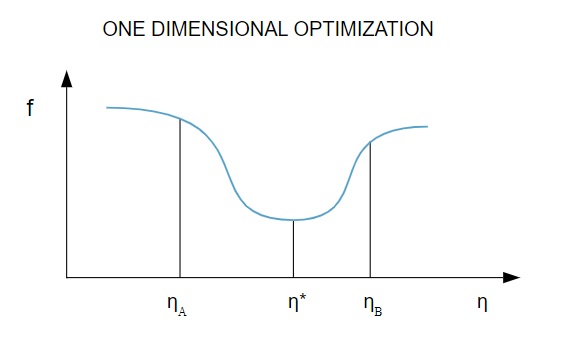
مصدر

في الرسم التخطيطي ، تحدد النقطتان η1 و 2 الفاصل الزمني الذي يحتوي على الحد الأدنى من f و η * .

وبالتالي ، تهدف طرق التحسين أحادية البعد إلى إيجاد الحد الأدنى من وظيفة أحادية البعد. اثنان من الخوارزميات أحادية البعد الأكثر استخدامًا هما طريقة المقطع الذهبي وطريقة برنت.

طريقة المقطع الذهبي

يتم استخدام خوارزمية البحث في القسم الذهبي للعثور على الحد الأدنى أو الأقصى لوظيفة ذات متغير واحد [ f (x) ]. إذا كنا نعلم بالفعل أن الوظيفة بها حد أدنى بين نقطتين ، فيمكننا إجراء بحث تكراري تمامًا كما نفعل في البحث عن جذر المعادلة f (x) = 0 . أيضًا ، إذا تمكنا من إيجاد ثلاث نقاط ( x0 <x1 <x2 ) تقابل f (x0)> f (x1)> f (X2) في جوار الحد الأدنى ، فيمكننا استنتاج وجود حد أدنى بين x0 و x2 . لمعرفة هذا الحد الأدنى ، يمكننا النظر في نقطة أخرى x3 بين x1 و x2 ، والتي ستعطينا النتائج التالية:

• إذا كانت f (x3) = f3a> f (x1) ، يكون الحد الأدنى داخل الفاصل الزمني x3 - x0 = a + c المرتبط بثلاث نقاط جديدة x0 <x1 <x3 (هنا يتم استبدال x2 بـ x3 ).
• إذا كانت f (x3) = f3b> f (x1 ) ، يكون الحد الأدنى داخل الفاصل الزمني x2 - x1 = b مرتبطًا بثلاث نقاط جديدة x1 <x3 <x2 (هنا يتم استبدال x0 بـ x1 ).

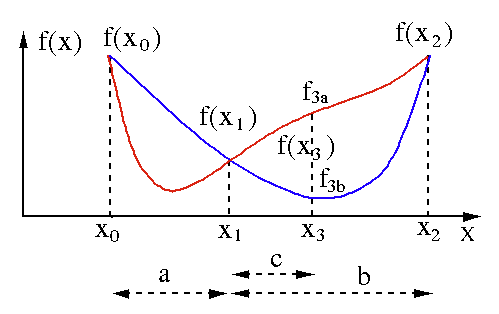
مصدر

طريقة برنت

طريقة برنت عبارة عن خوارزمية لاكتشاف الجذور تجمع بين أقواس الجذر ، والتقسيم ، والقطع ، والاستيفاء التربيعي المعكوس . على الرغم من أن هذه الخوارزمية تحاول استخدام طريقة القاطع سريعة التقارب أو الاستيفاء التربيعي العكسي كلما أمكن ذلك ، فإنها تعود عادةً إلى طريقة التقسيم. تم تطبيق طريقة Brent بلغة Wolfram ، ويتم التعبير عنها على النحو التالي:

الطريقة -> برنت في FindRoot [eqn، x، x0، x1].

في طريقة برنت ، نستخدم كثير حدود إقحام لاجرانج من الدرجة 2. في عام 1973 ، ادعى برنت أن هذه الطريقة ستتقارب دائمًا ، بشرط أن تكون قيم الدالة قابلة للحساب داخل منطقة معينة ، بما في ذلك الجذر. إذا كانت هناك ثلاث نقاط x1 و x2 و x3 ، فإن طريقة Brent تناسب x كدالة تربيعية لـ y ، باستخدام صيغة الاستيفاء:

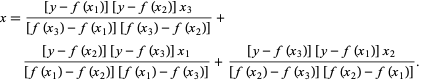
مصدر

يتم تحقيق تقديرات الجذر اللاحقة من خلال النظر ، وبالتالي إنتاج المعادلة التالية:

مصدر

هنا ، P = S [T (R - T) (x3 - x2) - (1 - R) (x2 -x1)] و Q = (T - 1) (R - 1) (S - 1) و ،

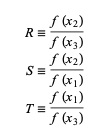
مصدر

2. التحسين متعدد الأبعاد

الآن ، نحن نعلم بالفعل أن مشكلة التعلم للشبكات العصبية تهدف إلى العثور على متجه المعلمة ( w * ) الذي تأخذ وظيفة الخسارة ( f ) قيمة دنيا له. وفقًا لتفويضات الشرط القياسي ، إذا كانت الشبكة العصبية عند الحد الأدنى من وظيفة الخسارة ، فإن التدرج هو المتجه الصفري.

نظرًا لأن وظيفة الخسارة هي وظيفة غير خطية للمعلمات ، فمن المستحيل العثور على خوارزميات التدريب المغلقة للحد الأدنى. ومع ذلك ، إذا نظرنا في البحث من خلال مساحة المعلمة التي تتضمن سلسلة من الخطوات ، في كل خطوة ، ستقل الخسارة عن طريق ضبط معلمات الشبكة العصبية.

في التحسين متعدد الأبعاد ، يتم تدريب الشبكة العصبية عن طريق اختيار متجه معلمة عشوائي ثم إنشاء سلسلة من المعلمات لضمان تقليل وظيفة الخسارة مع كل تكرار للخوارزمية. يُعرف هذا الاختلاف في الخسارة بين خطوتين لاحقتين باسم "إنقاص الخسارة". تستمر عملية إنقاص الخسارة حتى تصل خوارزمية التدريب أو تحقق الشرط المحدد.

فيما يلي ثلاثة أمثلة لخوارزميات التحسين متعددة الأبعاد:

نزول متدرج

ربما تكون خوارزمية النسب المتدرج هي أبسط خوارزميات التدريب. نظرًا لأنها تعتمد على المعلومات المقدمة `` من متجه التدرج ، فهي طريقة من الدرجة الأولى. في هذه الطريقة ، سنأخذ f [w (i)] = f (i) و ∇f [w (i)] = g (i) . نقطة البداية لخوارزمية التدريب هذه هي w (0) التي تستمر في التقدم حتى يتم استيفاء المعيار المحدد - تنتقل من w (i) إلى w (i + 1) في اتجاه التدريب d (i) = −g (i) . ومن ثم ، فإن نزول التدرج يتكرر على النحو التالي:

w (i + 1) = w (i) −g (i) η (i) ،

هنا ، أنا = 0،1 ، ...

تمثل المعلمة η معدل التدريب. يمكنك تعيين قيمة ثابتة لـ η أو تعيينها على القيمة التي تم العثور عليها بواسطة التحسين أحادي البعد على طول اتجاه التدريب في كل خطوة. ومع ذلك ، فمن المفضل تحديد القيمة المثلى لمعدل التدريب الذي تم تحقيقه عن طريق تصغير الخط في كل خطوة.

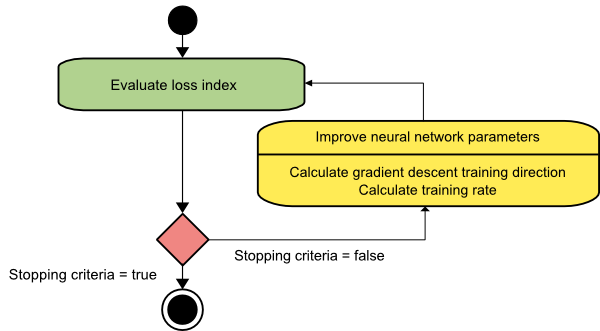
مصدر

تحتوي هذه الخوارزمية على العديد من القيود نظرًا لأنها تتطلب العديد من التكرارات للوظائف التي لها هياكل وادي طويلة وضيقة. بينما تتناقص دالة الخسارة بسرعة أكبر في اتجاه التدرج اللوني لأسفل المنحدرات ، فإنها لا تضمن دائمًا أسرع تقارب.

طريقة نيوتن

هذه خوارزمية من الدرجة الثانية لأنها تستفيد من مصفوفة هسه. تهدف طريقة نيوتن إلى إيجاد اتجاهات تدريب أفضل من خلال الاستفادة من المشتقات الثانية لوظيفة الخسارة. هنا ، سنشير إلى f [w (i)] = f (i) و ∇f [w (i)] = g (i) و Hf [w (i)] = H (i) . الآن ، سننظر في التقريب التربيعي لـ f عند w (0) باستخدام توسيع سلسلة تايلور ، مثل:

f = f (0) + g (0) ⋅ [w − w (0)] + 0.5⋅ [w − w (0)] 2⋅H (0)

هنا ، H (0) هي المصفوفة Hessian لـ f محسوبة عند النقطة w (0) . بالنظر إلى g = 0 للحد الأدنى من f (w) ، نحصل على المعادلة التالية:

ز = ز (0) + ح (0) ⋅ (ث − ث (0)) = 0

نتيجة لذلك ، يمكننا أن نرى أنه بدءًا من متجه المعلمة w (0) ، تتكرر طريقة نيوتن على النحو التالي:

w (i + 1) = w (i) −H (i) −1⋅g (i)

هنا ، i = 0،1 ، ... والمتجه H (i) −1⋅g (i) يشار إليه باسم "خطوة نيوتن". يجب أن تتذكر أن تغيير المعلمة قد يتحرك نحو الحد الأقصى بدلاً من السير في اتجاه الحد الأدنى. عادة ، يحدث هذا إذا لم تكن مصفوفة هس محددة موجبة ، مما يؤدي إلى تقليل تقييم الوظيفة في كل تكرار. ومع ذلك ، لتجنب هذه المشكلة ، نقوم عادةً بتعديل معادلة الطريقة على النحو التالي:

w (i + 1) = w (i) - (H (i) −1⋅g (i)) η

هنا ، أنا = 0،1 ،….

يمكنك إما ضبط معدل التدريب η على قيمة ثابتة أو القيمة التي تم الحصول عليها عبر تصغير الخط. لذا ، فإن المتجه d (i) = H (i) −1⋅g (i) يصبح اتجاه التدريب لطريقة نيوتن.

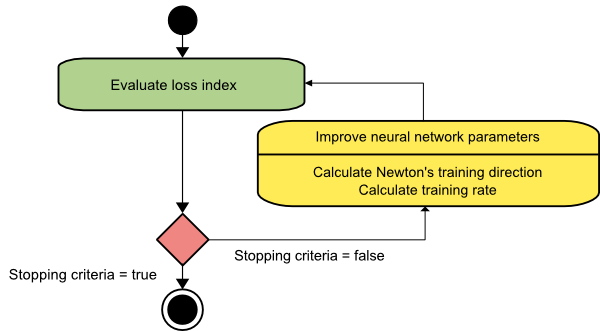
مصدر

العيب الرئيسي لطريقة نيوتن هو أن التقييم الدقيق لهيسان وعكسه حسابات باهظة الثمن للغاية.

المترافقة التدرج

تقع طريقة التدرج المترافق بين نزول التدرج وطريقة نيوتن. إنها خوارزمية وسيطة - بينما تهدف إلى تسريع عامل التقارب البطيء لطريقة نزول التدرج ، فإنها تلغي أيضًا الحاجة إلى متطلبات المعلومات المتعلقة بتقييم وتخزين وعكس مصفوفة هيس المطلوبة عادةً في طريقة نيوتن.

تقوم خوارزمية تدريب التدرج المترافق بالبحث في الاتجاهات المقترنة التي توفر تقاربًا أسرع من اتجاهات نزول التدرج. يتم تصريف اتجاهات التدريب هذه وفقًا لمصفوفة هس. هنا ، تشير d إلى متجه اتجاه التدريب. إذا بدأنا بمتجه المعلمة الأولية [w (0)] ومتجه اتجاه التدريب الأولي [d (0) = - g (0)] ، فإن طريقة التدرج المترافق تولد سلسلة من اتجاهات التدريب ممثلة على النحو التالي:

د (i + 1) = g (i + 1) + d (i) ⋅γ (i) ،

هنا ، i = 0،1 ، ... و هي المعلمة المرافقة. يتم إعادة تعيين اتجاه التدريب لجميع خوارزميات التدرج المترافق بشكل دوري إلى سالب التدرج. تم تحسين المعلمات ، ويتم تحقيق معدل التدريب ( η ) عن طريق تصغير الخط ، وفقًا للتعبير الموضح أدناه:

w (i + 1) = w (i) + d (i) ⋅η (i)

هنا ، أنا = 0،1 ، ...

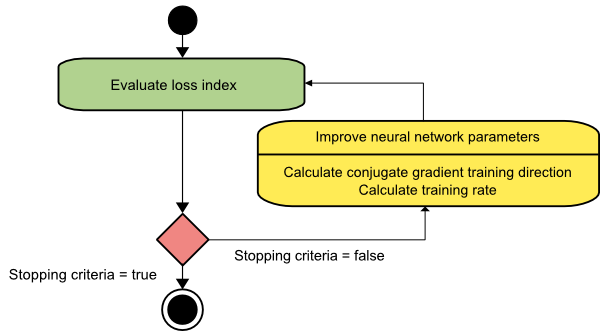
مصدر

خاتمة

كل خوارزمية تأتي مع مزايا وعيوب فريدة. هذه ليست سوى عدد قليل من الخوارزميات المستخدمة لتدريب الشبكات العصبية ، وتوضح وظائفها فقط قمة جبل الجليد - مع تقدم أطر التعلم العميق ، وكذلك وظائف هذه الخوارزميات.

إذا كنت مهتمًا بمعرفة المزيد عن الشبكة العصبية وبرامج التعلم الآلي والذكاء الاصطناعي ، فراجع برنامج IIIT-B & upGrad's Executive PG في التعلم الآلي والذكاء الاصطناعي المصمم للمهنيين العاملين ويقدم أكثر من 450 ساعة من التدريب الصارم ، 30+ دراسات الحالة والمهام ، وحالة خريجي IIIT-B ، وأكثر من 5 مشاريع تتويجا عملية ومساعدة وظيفية مع كبرى الشركات.