Neuronales Netzwerk: Architektur, Komponenten und Top-Algorithmen

Künstliche neuronale Netze (KNNs) sind ein wesentlicher Bestandteil des Deep-Learning-Prozesses. Sie sind von der neurologischen Struktur des menschlichen Gehirns inspiriert. Laut AILabPage sind ANNs „komplexer Computercode, der mit der Anzahl einfacher, hochgradig miteinander verbundener Verarbeitungselemente geschrieben wurde, die von der menschlichen biologischen Gehirnstruktur inspiriert sind, um die Arbeits- und Verarbeitungsdaten (Informationen) des menschlichen Gehirns zu simulieren“.

Melden Sie sich online für die besten Zertifizierungen für maschinelles Lernen von den besten Universitäten der Welt an – Master, Executive Post Graduate Programs und Advanced Certificate Program in ML & AI, um Ihre Karriere zu beschleunigen.

Deep Learning konzentriert sich auf fünf zentrale neuronale Netze, darunter:

• Mehrschichtiges Perzeptron
• Radiales Basisnetzwerk
• Wiederkehrende neuronale Netze
• Generative gegnerische Netzwerke
• Faltungsneuronale Netze.

Neuronales Netzwerk: Architektur

Neuronale Netze sind komplexe Strukturen aus künstlichen Neuronen, die mehrere Eingaben aufnehmen können, um eine einzige Ausgabe zu erzeugen. Dies ist die Hauptaufgabe eines neuronalen Netzwerks – Eingaben in sinnvolle Ausgaben umzuwandeln. Normalerweise besteht ein neuronales Netzwerk aus einer Eingabe- und einer Ausgabeschicht mit einer oder mehreren verborgenen Schichten darin.

In einem neuronalen Netzwerk beeinflussen sich alle Neuronen gegenseitig und sind daher alle miteinander verbunden. Das Netzwerk kann jeden Aspekt des vorliegenden Datensatzes erkennen und beobachten und wie die verschiedenen Teile der Daten miteinander in Beziehung stehen oder nicht. So sind Neuronale Netze in der Lage, extrem komplexe Muster in riesigen Datenmengen zu finden.

Lesen Sie: Maschinelles Lernen vs. neuronale Netze

In einem neuronalen Netzwerk erfolgt der Informationsfluss auf zwei Arten –

• Feedforward-Netzwerke: In diesem Modell wandern die Signale nur in eine Richtung zur Ausgangsschicht. Feedforward-Netzwerke haben eine Eingabeschicht und eine einzelne Ausgabeschicht mit null oder mehreren verborgenen Schichten. Sie werden häufig in der Mustererkennung verwendet.
• Rückkopplungsnetzwerke: In diesem Modell verwenden die wiederkehrenden oder interaktiven Netzwerke ihren internen Zustand (Speicher), um die Folge von Eingaben zu verarbeiten. In ihnen können Signale in beide Richtungen durch die Schleifen (verborgene Schicht/en) im Netzwerk laufen. Sie werden typischerweise in Zeitreihen und sequentiellen Aufgaben verwendet.

Neuronales Netzwerk: Komponenten

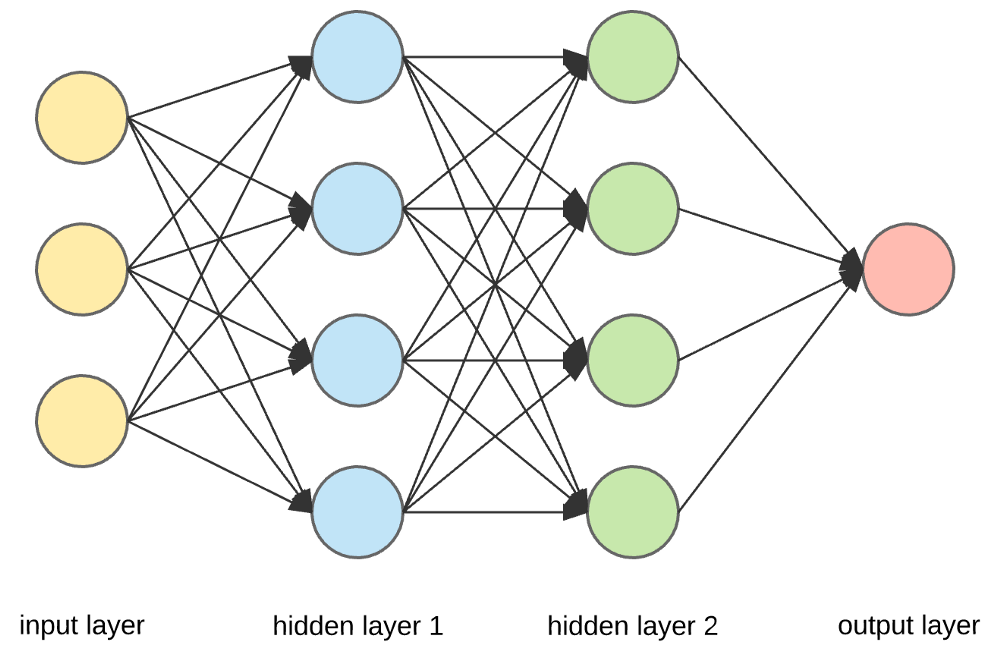
Quelle

Eingabeschichten, Neuronen und Gewichte –

Im obigen Bild ist die äußerste gelbe Schicht die Eingabeschicht. Ein Neuron ist die Grundeinheit eines neuronalen Netzes. Sie erhalten Eingaben von einer externen Quelle oder anderen Knoten. Jeder Knoten ist mit einem anderen Knoten aus der nächsten Schicht verbunden, und jede dieser Verbindungen hat ein bestimmtes Gewicht. Gewichtungen werden einem Neuron basierend auf seiner relativen Wichtigkeit gegenüber anderen Eingaben zugewiesen.

Wenn alle Knotenwerte aus der gelben Ebene multipliziert (zusammen mit ihrer Gewichtung) und zusammengefasst werden, wird ein Wert für die erste verborgene Ebene generiert. Basierend auf dem zusammengefassten Wert hat die blaue Schicht eine vordefinierte „Aktivierungs“-Funktion, die bestimmt, ob dieser Knoten „aktiviert“ wird oder nicht und wie „aktiv“ er sein wird.

Lassen Sie uns dies anhand einer einfachen alltäglichen Aufgabe verstehen – Tee kochen. Bei der Teezubereitung sind die zur Teezubereitung verwendeten Zutaten (Wasser, Teeblätter, Milch, Zucker und Gewürze) die „Neuronen“, da sie die Ausgangspunkte des Prozesses bilden. Die Menge jeder Zutat stellt das „Gewicht“ dar. Sobald Sie die Teeblätter in das Wasser geben und den Zucker, die Gewürze und die Milch in die Pfanne geben, vermischen sich alle Zutaten und verwandeln sich in einen anderen Zustand. Dieser Transformationsprozess stellt die „Aktivierungsfunktion“ dar.

Erfahren Sie mehr über: Deep Learning vs. neuronale Netze

Versteckte Ebenen und Ausgabeebene –

Die Schicht oder Schichten, die zwischen der Eingabe- und der Ausgabeschicht verborgen sind, wird als verborgene Schicht bezeichnet. Es wird die verborgene Schicht genannt, da es immer vor der Außenwelt verborgen ist. Die Hauptberechnung eines neuronalen Netzwerks findet in den verborgenen Schichten statt. Die verborgene Schicht nimmt also alle Eingaben aus der Eingabeschicht und führt die notwendige Berechnung durch, um ein Ergebnis zu generieren. Dieses Ergebnis wird dann an die Ausgabeschicht weitergeleitet, damit der Benutzer das Ergebnis der Berechnung sehen kann.

Wenn wir in unserem Teezubereitungsbeispiel alle Zutaten mischen, ändert die Formulierung beim Erhitzen ihren Zustand und ihre Farbe. Die Zutaten repräsentieren die verborgenen Schichten. Hier stellt das Erhitzen den Aktivierungsprozess dar, der schließlich das Ergebnis liefert – Tee.

Neuronales Netz: Algorithmen

In einem neuronalen Netzwerk wird der Lern- (oder Trainings-) Prozess initiiert, indem die Daten in drei verschiedene Sätze aufgeteilt werden:

• Trainingsdatensatz – Dieser Datensatz ermöglicht es dem neuronalen Netzwerk, die Gewichtungen zwischen Knoten zu verstehen.
• Validierungsdatensatz – Dieser Datensatz wird zur Feinabstimmung der Leistung des neuronalen Netzwerks verwendet.
• Testdatensatz – Dieser Datensatz wird verwendet, um die Genauigkeit und Fehlerspanne des neuronalen Netzwerks zu bestimmen.

Sobald die Daten in diese drei Teile segmentiert sind, werden neuronale Netzwerkalgorithmen darauf angewendet, um das neuronale Netzwerk zu trainieren. Das Verfahren zur Erleichterung des Trainingsprozesses in einem neuronalen Netzwerk wird als Optimierung bezeichnet, und der verwendete Algorithmus wird als Optimierer bezeichnet. Es gibt verschiedene Arten von Optimierungsalgorithmen, jeder mit seinen einzigartigen Eigenschaften und Aspekten wie Speicherbedarf, numerische Genauigkeit und Verarbeitungsgeschwindigkeit.

Bevor wir in die Diskussion der verschiedenen neuronalen Netzwerkalgorithmen eintauchen, wollen wir zuerst das Lernproblem verstehen.

Lesen Sie auch : Neuronale Netzwerkanwendungen in der realen Welt

Was ist das Lernproblem?

Wir stellen das Lernproblem durch die Minimierung eines Verlustindex ( f ) dar. Hier ist „ f “ die Funktion, die die Leistung eines neuronalen Netzwerks bei einem bestimmten Datensatz misst. Im Allgemeinen besteht der Verlustindex aus einem Fehlerterm und einem Regularisierungsterm. Während der Fehlerterm auswertet, wie ein neuronales Netzwerk zu einem Datensatz passt, hilft der Regularisierungsterm , das Problem der Überanpassung zu vermeiden, indem er die effektive Komplexität des neuronalen Netzwerks steuert.

Die Verlustfunktion [ f(w ) hängt von den adaptiven Parametern – Gewichtungen und Verzerrungen – des neuronalen Netzwerks ab. Diese Parameter können in einem einzigen n-dimensionalen Gewichtungsvektor ( w ) gruppiert werden.

Hier ist eine bildliche Darstellung der Verlustfunktion:

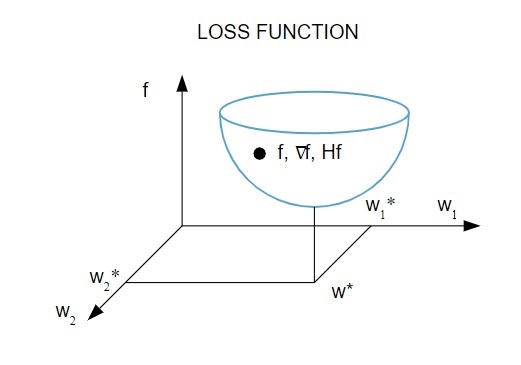
Quelle

Gemäß diesem Diagramm tritt das Minimum der Verlustfunktion am Punkt ( w* ) auf. Sie können jederzeit die erste und zweite Ableitung der Verlustfunktion berechnen. Die ersten Ableitungen sind im Gradientenvektor gruppiert und seine Komponenten werden wie folgt dargestellt:

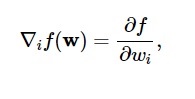
Quelle

Hier ist i = 1,…..,n .

Die zweiten Ableitungen der Verlustfunktion werden wie folgt in der Hesse-Matrix gruppiert:

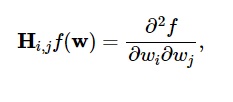
Quelle

Hier ist i,j = 0,1,…

Jetzt, da wir wissen, was das Lernproblem ist, können wir die fünf wichtigsten diskutieren

Algorithmen für neuronale Netzwerke .

1. Eindimensionale Optimierung

Da die Verlustfunktion von mehreren Parametern abhängt, sind eindimensionale Optimierungsmethoden beim Training neuronaler Netze von entscheidender Bedeutung. Trainingsalgorithmen berechnen zuerst eine Trainingsrichtung ( d ) und berechnen dann die Trainingsrate ( η ), die dabei hilft, den Verlust in der Trainingsrichtung [ f(η) ] zu minimieren.

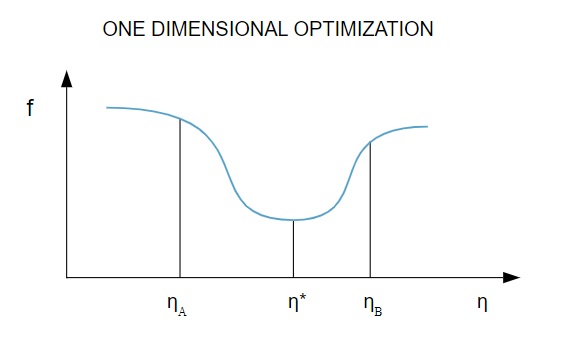
Quelle

Im Diagramm definieren die Punkte η1 und η2 das Intervall, das das Minimum von f, η* enthält .

Daher zielen eindimensionale Optimierungsverfahren darauf ab, das Minimum einer gegebenen eindimensionalen Funktion zu finden. Zwei der am häufigsten verwendeten eindimensionalen Algorithmen sind die Golden-Section-Methode und die Brent-Methode.

Methode des Goldenen Schnitts

Der Golden-Section-Suchalgorithmus wird verwendet, um das Minimum oder Maximum einer Funktion mit einer einzigen Variablen [ f(x) ] zu finden. Wenn wir bereits wissen, dass eine Funktion ein Minimum zwischen zwei Punkten hat, können wir eine iterative Suche durchführen, genau wie bei der Winkelhalbierungssuche nach der Wurzel einer Gleichung f(x) = 0 . Wenn wir außerdem drei Punkte ( x0 < x1 < x2 ) entsprechend f(x0) > f(x1) > f(X2) in der Nähe des Minimums finden, können wir daraus schließen, dass zwischen x0 und x2 ein Minimum existiert . Um dieses Minimum herauszufinden, können wir einen weiteren Punkt x3 zwischen x1 und x2 betrachten , was uns die folgenden Ergebnisse liefert:

• Wenn f(x3) = f3a > f(x1), liegt das Minimum innerhalb des Intervalls x3 – x0 = a + c , das mit drei neuen Punkten x0 < x1 < x3 verknüpft ist (hier wird x2 durch x3 ersetzt ).
• Wenn f(x3) = f3b > f(x1 ), liegt das Minimum innerhalb des Intervalls x2 – x1 = b bezogen auf drei neue Punkte x1 < x3 < x2 (hier wird x0 durch x1 ersetzt ).

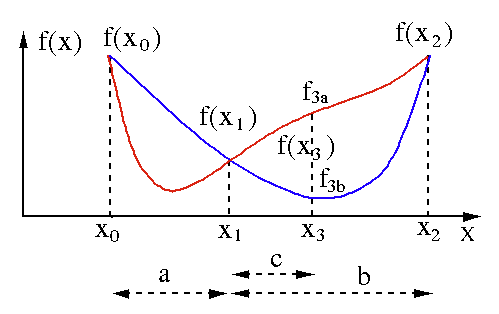
Quelle

Brents Methode

Die Brent-Methode ist ein Wurzelfindungsalgorithmus, der Wurzelklammerung , Halbierung , Sekante und inverse quadratische Interpolation kombiniert . Obwohl dieser Algorithmus versucht, wann immer möglich, die schnell konvergierende Sekantenmethode oder die inverse quadratische Interpolation zu verwenden, kehrt er normalerweise zur Halbierungsmethode zurück. In der Wolfram Language implementiert , wird Brents Methode wie folgt ausgedrückt:

Methode -> Brent in FindRoot [eqn, x, x0, x1].

Bei der Brent-Methode verwenden wir ein Lagrange-Interpolationspolynom 2. Grades. 1973 behauptete Brent, dass diese Methode immer konvergieren wird, vorausgesetzt, die Werte der Funktion sind innerhalb eines bestimmten Bereichs, einschließlich einer Wurzel, berechenbar. Wenn es drei Punkte x1, x2 und x3 gibt, passt die Brent-Methode x als quadratische Funktion von y unter Verwendung der Interpolationsformel an:

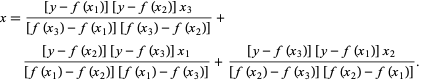
Quelle

Die nachfolgenden Wurzelschätzungen werden durch Betrachtung erreicht, wodurch sich die folgende Gleichung ergibt:

Quelle

Hier ist P = S [ T(R – T) (x3 – x2) – (1 – R) (x2 -x1) ] und Q = (T – 1) (R – 1) (S – 1) und,

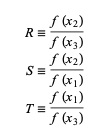
Quelle

2. Mehrdimensionale Optimierung

Inzwischen wissen wir bereits, dass das Lernproblem für neuronale Netze darauf abzielt, den Parametervektor ( w* ) zu finden, für den die Verlustfunktion ( f ) einen minimalen Wert annimmt. Gemäß den Vorschriften der Standardbedingung ist der Gradient der Nullvektor, wenn sich das neuronale Netzwerk auf einem Minimum der Verlustfunktion befindet.

Da die Verlustfunktion eine nichtlineare Funktion der Parameter ist, ist es unmöglich, die geschlossenen Trainingsalgorithmen für das Minimum zu finden. Wenn wir jedoch in Betracht ziehen, den Parameterraum zu durchsuchen, der eine Reihe von Schritten enthält, wird der Verlust bei jedem Schritt durch Anpassen der Parameter des neuronalen Netzwerks verringert.

Bei der mehrdimensionalen Optimierung wird ein neuronales Netzwerk trainiert, indem ein zufälliger we-Parametervektor ausgewählt und dann eine Folge von Parametern generiert wird, um sicherzustellen, dass die Verlustfunktion mit jeder Iteration des Algorithmus abnimmt. Diese Variation des Verlusts zwischen zwei aufeinanderfolgenden Schritten wird als „Verlustabnahme“ bezeichnet. Der Prozess der Verlustabnahme wird fortgesetzt, bis der Trainingsalgorithmus die spezifizierte Bedingung erreicht oder erfüllt.

Hier sind drei Beispiele für mehrdimensionale Optimierungsalgorithmen:

Gradientenabstieg

Der Gradientenabstiegsalgorithmus ist wahrscheinlich der einfachste aller Trainingsalgorithmen. Da es sich auf die bereitgestellten Informationen aus dem Gradientenvektor stützt, handelt es sich um ein Verfahren erster Ordnung. In dieser Methode nehmen wir f[w(i)] = f(i) und ∇f[w(i)] = g(i) . Ausgangspunkt dieses Trainingsalgorithmus ist w(0), der so lange fortschreitet, bis das vorgegebene Kriterium erfüllt ist – er bewegt sich von w(i) nach w(i+1) in Trainingsrichtung d(i) = −g(i) . Daher iteriert der Gradientenabstieg wie folgt:

w(i+1) = w(i)−g(i)η(i),

Hier ist i = 0,1,…

Der Parameter η repräsentiert die Trainingsrate. Sie können einen festen Wert für η festlegen oder ihn bei jedem Schritt auf den Wert setzen, der durch eindimensionale Optimierung entlang der Trainingsrichtung gefunden wird. Es wird jedoch bevorzugt, bei jedem Schritt den optimalen Wert für die Trainingsrate einzustellen, die durch Linienminimierung erreicht wird.

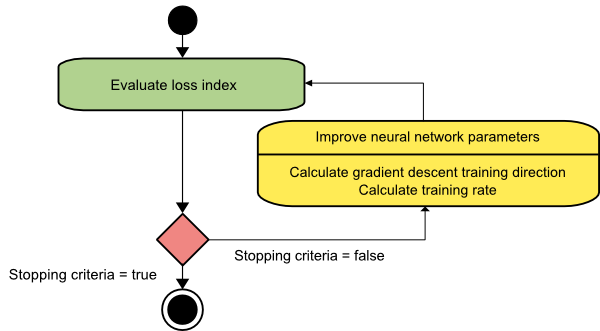
Quelle

Dieser Algorithmus hat viele Einschränkungen, da er zahlreiche Iterationen für Funktionen erfordert, die lange und schmale Talstrukturen haben. Die Verlustfunktion nimmt zwar am schnellsten in Richtung des Gefälles ab, sorgt aber nicht immer für die schnellste Konvergenz.

Newtons Methode

Dies ist ein Algorithmus zweiter Ordnung, da er die Hesse-Matrix nutzt. Das Newton-Verfahren zielt darauf ab, bessere Trainingsrichtungen zu finden, indem die zweiten Ableitungen der Verlustfunktion verwendet werden. Hier bezeichnen wir f[w(i)] = f(i), ∇f[w(i)]=g(i) und Hf[w(i)] = H(i) . Nun betrachten wir die quadratische Approximation von f bei w(0) unter Verwendung von Taylors Reihenentwicklung, etwa so:

f = f(0)+g(0)⋅[w−w(0)] + 0,5⋅[w−w(0)]2⋅H(0)

Hier ist H(0) die am Punkt w(0) berechnete hessische Matrix von f . Indem wir g = 0 für das Minimum von f(w) betrachten , erhalten wir die folgende Gleichung:

g = g(0)+H(0)⋅(w−w(0))=0

Als Ergebnis können wir sehen, dass ausgehend vom Parametervektor w(0) das Newton-Verfahren wie folgt iteriert:

w(i+1) = w(i)−H(i)−1⋅g(i)

Hier ist i = 0,1 ,… und der Vektor H(i)−1⋅g(i) wird als „Newton-Schritt“ bezeichnet. Sie müssen bedenken, dass sich die Parameteränderung in Richtung eines Maximums bewegen kann, anstatt in Richtung eines Minimums zu gehen. Normalerweise geschieht dies, wenn die Hesse-Matrix nicht positiv definit ist, wodurch die Funktionsauswertung bei jeder Iteration reduziert wird. Um dieses Problem zu vermeiden, ändern wir die Methodengleichung jedoch normalerweise wie folgt:

w(i+1) = w(i)−(H(i)−1⋅g(i))η

Hier ist i = 0,1 ,….

Sie können die Trainingsrate η entweder auf einen festen Wert oder auf den durch Linienminimierung erhaltenen Wert setzen. Somit wird der Vektor d(i)=H(i)−1⋅g(i) zur Trainingsrichtung für das Newton-Verfahren.

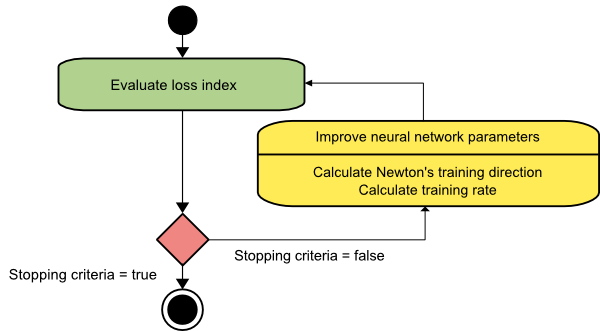
Quelle

Der Hauptnachteil von Newtons Methode besteht darin, dass die exakte Berechnung des Hessischen und seiner Inversen ziemlich teure Berechnungen sind.

Gradient konjugieren

Die konjugierte Gradientenmethode liegt zwischen der Gradientenabstiegs- und der Newton-Methode. Es handelt sich um einen Zwischenalgorithmus – er zielt zwar darauf ab, den langsamen Konvergenzfaktor des Gradientenabstiegsverfahrens zu beschleunigen, beseitigt aber auch die Notwendigkeit der Informationsanforderungen bezüglich der Auswertung, Speicherung und Inversion der Hesse-Matrix, die normalerweise beim Newton-Verfahren erforderlich sind.

Der konjugierte Gradienten-Trainingsalgorithmus führt die Suche in den konjugierten Richtungen durch, die eine schnellere Konvergenz liefert als Gradientenabstiegsrichtungen. Diese Trainingsrichtungen werden gemäß der Hesse-Matrix konjugiert. Dabei bezeichnet d den Trainingsrichtungsvektor. Wenn wir mit einem anfänglichen Parametervektor [w(0)] und einem anfänglichen Trainingsrichtungsvektor [d(0)=−g(0)] beginnen, erzeugt das konjugierte Gradientenverfahren eine Folge von Trainingsrichtungen, dargestellt als:

d(i+1) = g(i+1)+d(i)⋅γ(i),

Hier ist i = 0,1 ,… und γ ist der konjugierte Parameter. Die Trainingsrichtung für alle konjugierten Gradientenalgorithmen wird periodisch auf das Negative des Gradienten zurückgesetzt. Die Parameter werden verbessert und die Trainingsrate ( η ) wird durch Linienminimierung gemäß dem unten gezeigten Ausdruck erreicht:

w(i+1) = w(i)+d(i)⋅η(i)

Hier ist i = 0,1 ,…

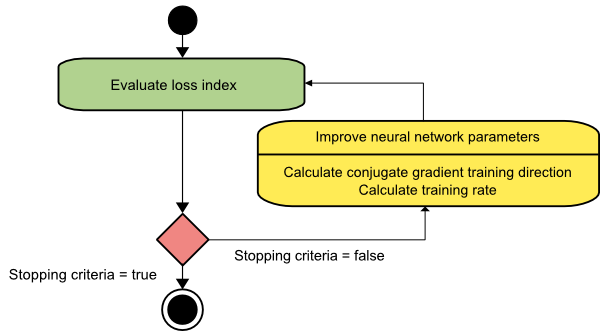
Quelle

Fazit

Jeder Algorithmus hat einzigartige Vor- und Nachteile. Dies sind nur einige Algorithmen, die zum Trainieren neuronaler Netze verwendet werden, und ihre Funktionen zeigen nur die Spitze des Eisbergs – mit der Weiterentwicklung der Deep-Learning-Frameworks werden auch die Funktionalitäten dieser Algorithmen zunehmen.

Wenn Sie mehr über neuronale Netze, maschinelle Lernprogramme und KI erfahren möchten, sehen Sie sich das Executive PG-Programm in maschinellem Lernen und KI von IIIT-B & upGrad an, das für Berufstätige konzipiert ist und mehr als 450 Stunden strenges Training bietet, 30+ Fallstudien und Aufgaben, IIIT-B-Alumni-Status, mehr als 5 praktische, praktische Abschlussprojekte und Arbeitsunterstützung bei Top-Unternehmen.