神经网络：架构、组件和顶级算法

人工神经网络(ANN) 是深度学习过程中不可或缺的一部分。 它们的灵感来自人类大脑的神经结构。 根据AILabPage的说法，人工神经网络是“由许多简单、高度互连的处理元素编写的复杂计算机代码，其灵感来自人类生物大脑结构，用于模拟人脑工作和处理数据（信息）模型。”

在线加入来自世界顶级大学的最佳机器学习认证——机器学习和人工智能领域的硕士、高管研究生课程和高级证书课程，以加快您的职业生涯。

深度学习专注于五个核心神经网络，包括：

• 多层感知器
• 径向基网络
• 递归神经网络
• 生成对抗网络
• 卷积神经网络。

神经网络：架构

神经网络是由人工神经元组成的复杂结构，可以接收多个输入以产生单个输出。 这是神经网络的主要工作——将输入转换为有意义的输出。 通常，神经网络由一个输入和输出层组成，其中包含一个或多个隐藏层。

在神经网络中，所有的神经元都相互影响，因此它们都是相互连接的。 网络可以确认和观察手头数据集的各个方面，以及数据的不同部分如何相互关联或不相互关联。 这就是神经网络能够在大量数据中找到极其复杂的模式的方式。

阅读：机器学习与神经网络

在神经网络中，信息流以两种方式发生——

• 前馈网络：在此模型中，信号仅沿一个方向传播，朝向输出层。 前馈网络有一个输入层和一个带有零个或多个隐藏层的输出层。 它们广泛用于模式识别。
• 反馈网络：在这个模型中，循环或交互网络使用它们的内部状态（记忆）来处理输入序列。 在它们中，信号可以通过网络中的环路（隐藏层）双向传播。 它们通常用于时间序列和顺序任务。

神经网络：组件

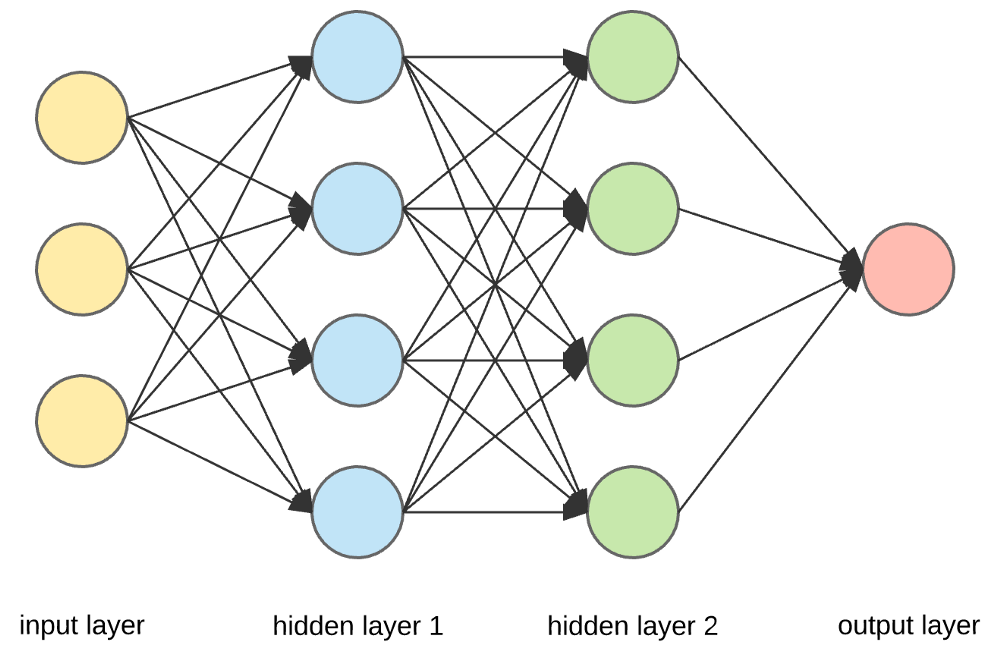
资源

输入层、神经元和权重——

在上面给出的图片中，最外面的黄色层是输入层。 神经元是神经网络的基本单元。 它们接收来自外部源或其他节点的输入。 每个节点都与下一层的另一个节点相连，每个这样的连接都有一个特定的权重。 根据神经元相对于其他输入的相对重要性，将权重分配给神经元。

当黄色层的所有节点值相乘（连同它们的权重）并汇总时，它会为第一个隐藏层生成一个值。 根据汇总的值，蓝色层有一个预定义的“激活”函数，它决定了这个节点是否会被“激活”以及它的“激活”程度。

让我们通过一个简单的日常任务来理解这一点——泡茶。 在制茶过程中，用于制茶的原料（水、茶叶、牛奶、糖和香料）是“神经元”，因为它们构成了过程的起点。 每种成分的量代表“重量”。 一旦你将茶叶放入水中，并在锅中加入糖、香料和牛奶，所有成分都会混合并转变为另一种状态。 这个转化过程代表了“激活功能”。

了解：深度学习与神经网络

隐藏层和输出层——

隐藏在输入和输出层之间的一层或多层称为隐藏层。 它被称为隐藏层，因为它总是对外部世界隐藏。 神经网络的主要计算发生在隐藏层中。 因此，隐藏层从输入层获取所有输入并执行必要的计算以生成结果。 然后将该结果转发到输出层，以便用户查看计算结果。

在我们的制茶示例中，当我们混合所有成分时，配方会在加热时改变其状态和颜色。 成分代表隐藏层。 在这里，加热代表了最终产生结果的激活过程——茶。

神经网络：算法

在神经网络中，学习（或训练）过程是通过将数据分成三个不同的集合来启动的：

• 训练数据集——该数据集允许神经网络了解节点之间的权重。
• 验证数据集——该数据集用于微调神经网络的性能。
• 测试数据集——该数据集用于确定神经网络的准确性和误差范围。

一旦数据被分割成这三个部分，神经网络算法就会应用于它们以训练神经网络。 用于促进神经网络中训练过程的过程称为优化，所使用的算法称为优化器。 有不同类型的优化算法，每种算法都有其独特的特征和方面，例如内存要求、数值精度和处理速度。

在我们深入讨论不同的神经网络算法之前，让我们先了解一下学习问题。

另请阅读：现实世界中的神经网络应用

什么是学习问题？

我们根据损失指数( f )的最小化来表示学习问题。 这里，“ f ”是衡量神经网络在给定数据集上的性能的函数。 通常，损失指标由误差项和正则化项组成。 虽然误差项评估神经网络如何拟合数据集，但正则化项通过控制神经网络的有效复杂性来帮助防止过度拟合问题。

损失函数 [ f(w ] 取决于神经网络的自适应参数——权重和偏差。这些参数可以分组为单个 n 维权重向量 ( w )。

这是损失函数的图形表示：

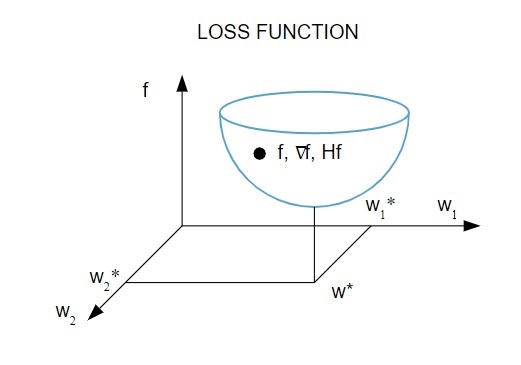
资源

根据该图，损失函数的最小值出现在点 ( w* )。 在任何时候，您都可以计算损失函数的一阶和二阶导数。 一阶导数在梯度向量中分组，其分量表示为：

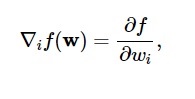
资源

在这里， i = 1,…..,n 。

损失函数的二阶导数在Hessian 矩阵中分组，如下所示：

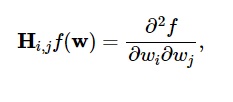
资源

这里， i,j = 0,1,…

现在我们知道了学习问题是什么，我们可以讨论五个主要问题

神经网络算法。

1.一维优化

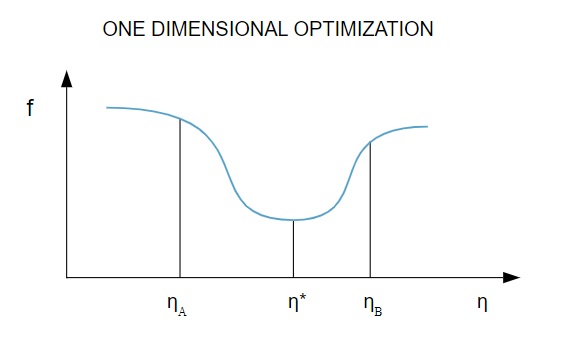
由于损失函数取决于多个参数，因此一维优化方法有助于训练神经网络。 训练算法首先计算训练方向 ( d )，然后计算有助于最小化训练方向损失的训练率 ( η ) [ f(η) ]。

资源

在图中，点 η1 和 η2 定义了包含f 的最小值 η*的区间。

因此，一维优化方法旨在找到给定一维函数的最小值。 最常用的两种一维算法是黄金分割法和布伦特法。

黄金分割法

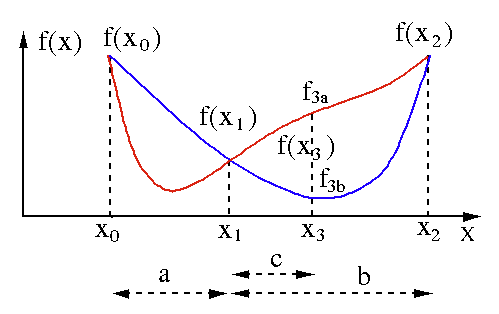
黄金分割搜索算法用于查找单变量函数 [ f(x) ] 的最小值或最大值。 如果我们已经知道函数在两点之间具有最小值，那么我们可以执行迭代搜索，就像我们在对等式f(x) = 0的根的二等分搜索中所做的那样。 另外，如果我们可以在最小值的邻域找到对应于f(x0) > f(x1) > f(X2)的三个点 ( x0 < x1 < x2 ) ，那么我们可以推断出x0和x2之间存在一个最小值. 为了找出这个最小值，我们可以考虑x1和x2之间的另一个点x3 ，这将给我们以下结果：

• 如果f(x3) = f3a > f(x1)，最小值在与三个新点x0 < x1 < x3相关的区间x3 – x0 = a + c内（这里x2被x3替换）。
• 如果f(x3) = f3b > f(x1 )，最小值在区间x2 – x1 = b内，与三个新点x1 < x3 < x2相关（这里x0被x1替换）。

资源

布伦特方法

Brent 方法是一种求根算法，它结合了根包围、二等分、割线和反二次插值。 尽管该算法尽可能尝试使用快速收敛割线法或反二次插值法，但它通常会恢复为二等分法。 在Wolfram 语言中实现的 Brent 方法表示为：

方法 -> FindRoot [eqn, x, x0, x1] 中的 Brent。

在 Brent 的方法中，我们使用2 次拉格朗日插值多项式。1973年，Brent 声称该方法将始终收敛，前提是函数的值在特定区域内是可计算的，包括根。 如果存在三个点x1、x2和x3 ，则 Brent 方法使用插值公式将x拟合为y的二次函数：

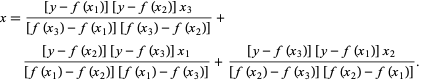
资源

随后的根估计是通过考虑来实现的，从而产生以下等式：

资源

这里， P = S [ T(R – T) (x3 – x2) – (1 – R) (x2 -x1) ]和Q = (T – 1) (R – 1) (S – 1) 并且，

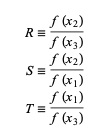
资源

2.多维优化

到目前为止，我们已经知道神经网络的学习问题旨在找到损失函数 ( f ) 取最小值的参数向量 ( w* )。 根据标准条件的要求，如果神经网络处于损失函数的最小值，则梯度为零向量。

由于损失函数是参数的非线性函数，因此不可能找到最小值的封闭训练算法。 但是，如果我们考虑在包含一系列步骤的参数空间中进行搜索，则在每一步中，通过调整神经网络的参数，损失都会减少。

在多维优化中，通过选择一个随机参数向量然后生成一系列参数来训练神经网络，以确保损失函数随着算法的每次迭代而减小。 两个后续步骤之间的这种损失变化称为“损失递减”。 损失递减过程一直持续到训练算法达到或满足指定条件。

以下是多维优化算法的三个示例：

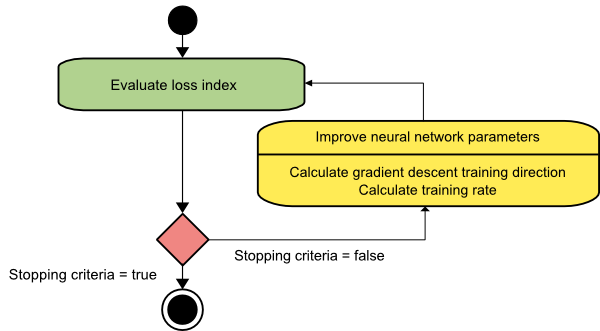
梯度下降

梯度下降算法可能是所有训练算法中最简单的。 因为它依赖于梯度向量提供的信息，所以它是一阶方法。 在这种方法中，我们将采用f[w(i)] = f(i)和∇f[w(i)] = g(i) 。 该训练算法的起点是 w(0)，它会一直进行直到满足指定的标准——它在训练方向上从 w(i) 移动到 w(i+1) d(i) = -g(i) . 因此，梯度下降迭代如下：

w(i+1) = w(i)-g(i)η(i),

在这里，我 = 0,1，…

参数η表示训练率。 您可以为η设置一个固定值或将其设置为在每一步沿训练方向进行一维优化找到的值。 但是，最好为每一步通过线最小化实现的训练率设置最佳值。

资源

该算法有许多限制，因为它需要对具有长而窄的谷结构的函数进行多次迭代。 虽然损失函数在下坡梯度方向下降得最快，但它并不总是确保最快的收敛。

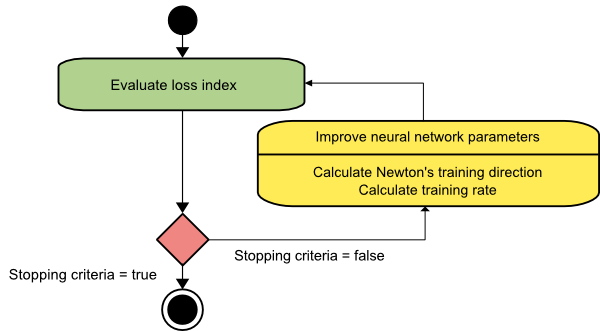
牛顿法

这是一个二阶算法，因为它利用了 Hessian 矩阵。 牛顿的方法旨在通过利用损失函数的二阶导数找到更好的训练方向。 在这里，我们将表示f[w(i)] = f(i)、∇f[w(i)]=g(i)和Hf[w(i)] = H(i) 。 现在，我们将使用泰勒级数展开来考虑f在w(0)处的二次逼近，如下所示：

f = f(0)+g(0)⋅[w−w(0)] + 0.5⋅[w−w(0)]2⋅H(0)

这里， H(0)是在点w(0)处计算的f的 Hessian 矩阵。 通过考虑g = 0的最小值f(w) ，我们得到以下等式：

g = g(0)+H(0)⋅(w−w(0))=0

结果，我们可以看到，从参数向量w(0)开始，牛顿的方法迭代如下：

w(i+1) = w(i)−H(i)−1⋅g(i)

这里， i = 0,1 ,… 并且向量H(i)−1⋅g(i)被称为“牛顿步长”。 您必须记住，参数变化可能会向最大值移动，而不是向最小值方向移动。 通常，如果 Hessian 矩阵不是正定的，就会发生这种情况，从而导致函数评估在每次迭代时减少。 但是，为了避免这个问题，我们通常将方法方程修改如下：

w(i+1) = w(i)−(H(i)−1⋅g(i))η

在这里，我 = 0,1 ,...。

您可以将训练率 η 设置为固定值或通过线最小化获得的值。 因此，向量d(i)=H(i)−1⋅g(i)成为牛顿法的训练方向。

资源

牛顿方法的主要缺点是 Hessian 及其逆的精确计算是相当昂贵的计算。

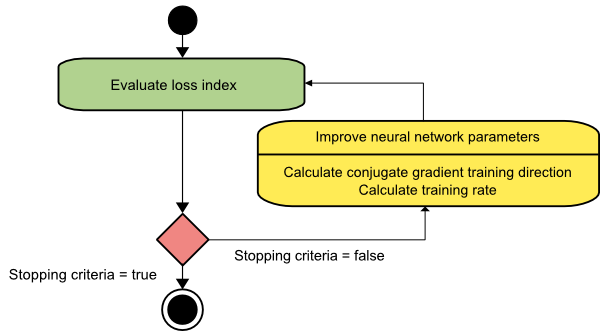
共轭梯度

共轭梯度法介于梯度下降法和牛顿法之间。 它是一种中间算法——虽然它旨在加速梯度下降法的缓慢收敛因子，但它也消除了牛顿法中通常需要的有关 Hessian 矩阵的评估、存储和求逆的信息需求。

共轭梯度训练算法在共轭方向上执行搜索，比梯度下降方向提供更快的收敛。 这些训练方向是根据 Hessian 矩阵共轭的。 这里，d 表示训练方向向量。 如果我们从一个初始参数向量 [w(0)] 和一个初始训练方向向量[d(0)=−g(0)]开始，共轭梯度方法会生成一个训练方向序列，表示为：

d(i+1) = g(i+1)+d(i)⋅γ(i),

这里， i = 0,1 ,… 和 γ 是共轭参数。 所有共轭梯度算法的训练方向都会定期重置为梯度的负值。 参数得到改进，训练率（ η ）通过线最小化来实现，根据如下所示的表达式：

w(i+1) = w(i)+d(i)⋅η(i)

在这里，我 = 0,1 ，...

资源

结论

每种算法都有独特的优点和缺点。 这些只是用于训练神经网络的少数算法，它们的功能只展示了冰山一角——随着深度学习框架的进步，这些算法的功能也会随之进步。

如果您有兴趣了解有关神经网络、机器学习程序和 AI的更多信息，请查看 IIIT-B 和 upGrad 的机器学习和 AI 执行 PG 计划，该计划专为工作专业人士设计，提供 450 多个小时的严格培训，30 多个案例研究和作业、IIIT-B 校友身份、5 个以上实用的实践顶点项目和顶级公司的工作协助。