โครงข่ายประสาทเทียม: สถาปัตยกรรม ส่วนประกอบ และอัลกอริทึมยอดนิยม

โครงข่ายประสาทเทียม (ANN) เป็นส่วนสำคัญของกระบวนการเรียนรู้เชิงลึก พวกเขาได้รับแรงบันดาลใจจากโครงสร้างทางระบบประสาทของสมองมนุษย์ ตาม AILabPage ANNs เป็น "รหัสคอมพิวเตอร์ที่ซับซ้อนซึ่งเขียนด้วยองค์ประกอบการประมวลผลที่เรียบง่ายและเชื่อมต่อถึงกันสูงจำนวนหนึ่งซึ่งได้รับแรงบันดาลใจจากโครงสร้างสมองทางชีววิทยาของมนุษย์สำหรับการจำลองการทำงานของสมองของมนุษย์และการประมวลผลข้อมูล (ข้อมูล)"

เข้าร่วม Best Machine Learning Certifications ทางออนไลน์จากมหาวิทยาลัยชั้นนำของโลก – Masters, Executive Post Graduate Programs และ Advanced Certificate Program ใน ML & AI เพื่อติดตามอาชีพของคุณอย่างรวดเร็ว

Deep Learning มุ่งเน้นไปที่ห้าโครงข่ายประสาทเทียมหลัก ได้แก่ :

• Perceptron หลายชั้น
• เครือข่าย Radial Basis
• โครงข่ายประสาทกำเริบ
• เครือข่ายปฏิปักษ์ทั่วไป
• โครงข่ายประสาท Convolutional

โครงข่ายประสาทเทียม: สถาปัตยกรรม

โครงข่ายประสาทเทียมเป็นโครงสร้างที่ซับซ้อนซึ่งทำจากเซลล์ประสาทเทียมที่สามารถรับอินพุตหลายตัวเพื่อสร้างเอาต์พุตเดียว นี่เป็นงานหลักของ Neural Network - เพื่อแปลงอินพุตเป็นเอาต์พุตที่มีความหมาย โดยปกติ Neural Network จะประกอบด้วยชั้นอินพุตและเอาต์พุตที่มีเลเยอร์ที่ซ่อนอยู่ภายในหนึ่งหรือหลายชั้น

ในโครงข่ายประสาทเทียม เซลล์ประสาททั้งหมดมีอิทธิพลซึ่งกันและกัน และด้วยเหตุนี้ เซลล์ประสาททั้งหมดจึงเชื่อมต่อกัน เครือข่ายสามารถรับทราบและสังเกตทุก ๆ แง่มุมของชุดข้อมูลในมือ และว่าส่วนต่าง ๆ ของข้อมูลอาจเกี่ยวข้องหรือไม่เกี่ยวข้องกันอย่างไร นี่คือวิธีที่ Neural Networks สามารถค้นหารูปแบบที่ซับซ้อนอย่างมากในข้อมูลปริมาณมหาศาล

อ่าน: การเรียนรู้ของเครื่องกับโครงข่ายประสาทเทียม

ใน Neural Network การไหลของข้อมูลเกิดขึ้นได้สองวิธี -

• เครือข่ายฟีดฟอร์เวิร์ด: ในโมเดลนี้ สัญญาณเดินทางในทิศทางเดียวเท่านั้น ไปยังเลเยอร์เอาต์พุต Feedforward Networks มีชั้นอินพุตและเอาต์พุตชั้นเดียวที่มีเลเยอร์ที่ซ่อนอยู่เป็นศูนย์หรือหลายชั้น มีการใช้กันอย่างแพร่หลายในการจดจำรูปแบบ
• เครือข่ายคำติชม: ในรูปแบบนี้ เครือข่ายที่เกิดซ้ำหรือแบบโต้ตอบใช้สถานะภายใน (หน่วยความจำ) เพื่อประมวลผลลำดับของอินพุต ในนั้น สัญญาณสามารถเดินทางในทั้งสองทิศทางผ่านลูป (เลเยอร์ที่ซ่อนอยู่) ในเครือข่าย โดยทั่วไปจะใช้ในอนุกรมเวลาและงานตามลำดับ

โครงข่ายประสาทเทียม: ส่วนประกอบ

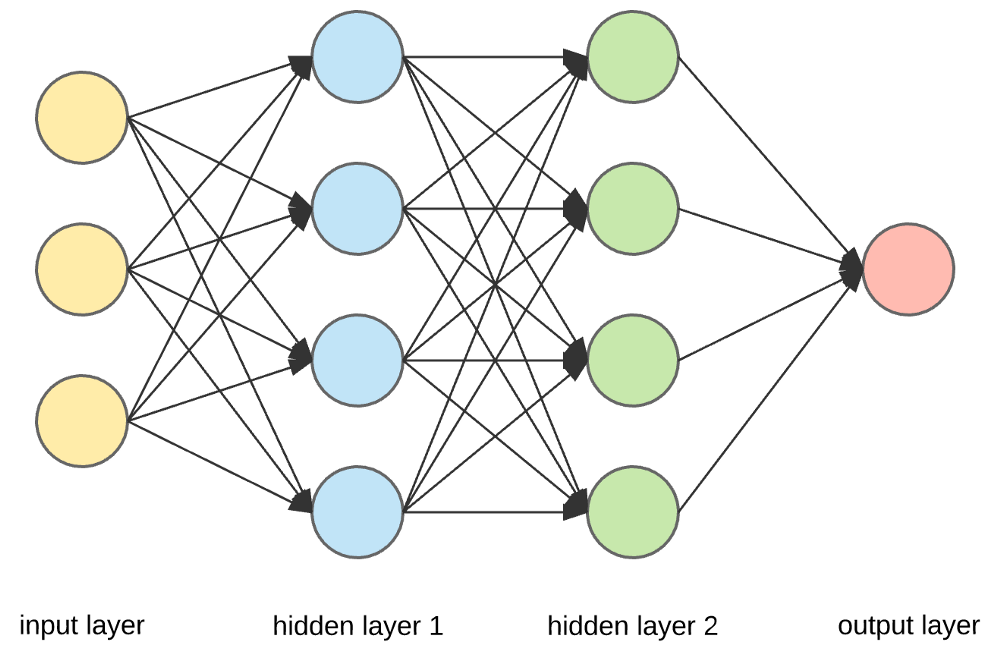
แหล่งที่มา

อินพุตเลเยอร์ เซลล์ประสาท และตุ้มน้ำหนัก –

ในภาพด้านบน เลเยอร์สีเหลืองด้านนอกสุดคือเลเยอร์อินพุต เซลล์ประสาทเป็นหน่วยพื้นฐานของโครงข่ายประสาทเทียม พวกเขารับอินพุตจากแหล่งภายนอกหรือโหนดอื่น แต่ละโหนดเชื่อมต่อกับโหนดอื่นจากเลเยอร์ถัดไป และแต่ละการเชื่อมต่อดังกล่าวมีน้ำหนักเฉพาะ น้ำหนักถูกกำหนดให้กับเซลล์ประสาทตามความสำคัญสัมพัทธ์กับปัจจัยการผลิตอื่นๆ

เมื่อค่าโหนดทั้งหมดจากเลเยอร์สีเหลืองถูกคูณ (พร้อมกับน้ำหนัก) และสรุป จะสร้างค่าสำหรับเลเยอร์แรกที่ซ่อนอยู่ ตามค่าสรุป เลเยอร์สีน้ำเงินมีฟังก์ชัน "การเปิดใช้งาน" ที่กำหนดไว้ล่วงหน้า ซึ่งกำหนดว่าโหนดนี้จะ "เปิดใช้งาน" หรือไม่และจะ "ใช้งาน" อย่างไร

มาทำความเข้าใจกับสิ่งนี้โดยใช้งานง่ายๆ ในชีวิตประจำวัน – ชงชา ในกระบวนการผลิตชา ส่วนผสมที่ใช้ทำชา (น้ำ ใบชา นม น้ำตาล และเครื่องเทศ) คือ "เซลล์ประสาท" เนื่องจากเป็นจุดเริ่มต้นของกระบวนการ ปริมาณของส่วนผสมแต่ละอย่างแสดงถึง "น้ำหนัก" เมื่อคุณใส่ใบชาลงในน้ำแล้วใส่น้ำตาล เครื่องเทศ และนมลงในกระทะ ส่วนผสมทั้งหมดจะผสมและเปลี่ยนเป็นสภาพอื่น กระบวนการแปลงนี้แสดงถึง "ฟังก์ชันการเปิดใช้งาน"

เรียนรู้เกี่ยวกับ: การเรียนรู้เชิงลึกกับโครงข่ายประสาทเทียม

เลเยอร์ที่ซ่อนอยู่และเลเยอร์เอาต์พุต –

เลเยอร์หรือเลเยอร์ที่ซ่อนอยู่ระหว่างเลเยอร์อินพุตและเอาต์พุตเรียกว่าเลเยอร์ที่ซ่อนอยู่ เรียกว่าชั้นซ่อนเร้นเพราะถูกซ่อนจากโลกภายนอกเสมอ การคำนวณหลักของ Neural Network เกิดขึ้นในเลเยอร์ที่ซ่อนอยู่ ดังนั้น เลเยอร์ที่ซ่อนอยู่จะรับอินพุตทั้งหมดจากเลเยอร์อินพุต และทำการคำนวณที่จำเป็นเพื่อสร้างผลลัพธ์ ผลลัพธ์นี้จะถูกส่งต่อไปยังชั้นผลลัพธ์เพื่อให้ผู้ใช้สามารถดูผลลัพธ์ของการคำนวณได้

ในตัวอย่างการชงชาของเรา เมื่อเราผสมส่วนผสมทั้งหมด สูตรจะเปลี่ยนสถานะและสีเมื่อให้ความร้อน ส่วนผสมแสดงถึงชั้นที่ซ่อนอยู่ การให้ความร้อนที่นี่แสดงถึงกระบวนการกระตุ้นที่ส่งผลในที่สุด นั่นคือ ชา

โครงข่ายประสาทเทียม: อัลกอริทึม

ในโครงข่ายประสาทเทียม กระบวนการเรียนรู้ (หรือการฝึกอบรม) เริ่มต้นโดยการแบ่งข้อมูลออกเป็นสามชุดที่แตกต่างกัน:

• ชุดข้อมูลการฝึกอบรม – ชุด ข้อมูลนี้ช่วยให้ Neural Network เข้าใจน้ำหนักระหว่างโหนด
• ชุดข้อมูลการตรวจสอบ – ชุดข้อมูลนี้ใช้สำหรับปรับแต่งประสิทธิภาพของ Neural Network
• ชุดข้อมูลทดสอบ – ชุดข้อมูลนี้ใช้เพื่อกำหนดความถูกต้องและระยะขอบของข้อผิดพลาดของ Neural Network

เมื่อข้อมูลถูกแบ่งออกเป็นสามส่วนแล้ว อัลกอริธึมของ Neural Network จะถูกนำไปใช้กับพวกมันเพื่อฝึกอบรม Neural Network ขั้นตอนที่ใช้สำหรับอำนวยความสะดวกในกระบวนการฝึกอบรมใน Neural Network เรียกว่าการเพิ่มประสิทธิภาพ และอัลกอริทึมที่ใช้เรียกว่าเครื่องมือเพิ่มประสิทธิภาพ อัลกอริธึมการเพิ่มประสิทธิภาพมีหลายประเภท แต่ละประเภทมีลักษณะเฉพาะและลักษณะเฉพาะ เช่น ข้อกำหนดหน่วยความจำ ความแม่นยำเชิงตัวเลข และความเร็วในการประมวลผล

ก่อนที่เราจะเจาะลึกในการอภิปรายเกี่ยวกับ อัลกอริทึม Neural Network ต่างๆ มาทำความเข้าใจปัญหาการเรียนรู้กันก่อน

อ่าน เพิ่มเติม : แอปพลิเคชั่น Neural Network ในโลกแห่งความจริง

ปัญหาการเรียนรู้คืออะไร?

เราเป็นตัวแทนของปัญหาการเรียนรู้ในแง่ของการลด ดัชนีการสูญเสีย ( f ) ในที่นี้ “ f ” คือฟังก์ชันที่ใช้วัดประสิทธิภาพของ Neural Network ในชุดข้อมูลที่กำหนด โดยทั่วไป ดัชนีการสูญเสียประกอบด้วยเงื่อนไขข้อผิดพลาดและระยะการทำให้เป็นมาตรฐาน แม้ว่าเงื่อนไข ข้อผิดพลาด จะประเมินว่า Neural Network เหมาะสมกับชุดข้อมูลอย่างไร ระยะ การทำให้เป็นมาตรฐาน จะช่วยป้องกันปัญหาการ overfitting โดยการควบคุมความซับซ้อนที่มีประสิทธิผลของ Neural Network

ฟังก์ชั่นการสูญเสีย [ f(w ] ขึ้นกับพารามิเตอร์ adaptative – น้ำหนักและอคติ – ของ Neural Network พารามิเตอร์เหล่านี้สามารถจัดกลุ่มเป็นเวกเตอร์น้ำหนัก n มิติเดียว ( w )

นี่คือการแสดงภาพของฟังก์ชันการสูญเสีย:

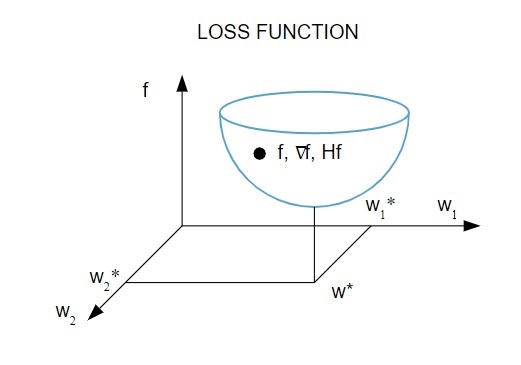
แหล่งที่มา

ตามแผนภาพนี้ ฟังก์ชันการสูญเสียขั้นต่ำจะเกิดขึ้นที่จุด ( w* ) คุณสามารถคำนวณอนุพันธ์ที่หนึ่งและสองของฟังก์ชันการสูญเสียได้ตลอดเวลา อนุพันธ์อันดับ 1 ถูกจัดกลุ่มในเวกเตอร์การไล่ระดับสีและองค์ประกอบของมันแสดงเป็น:

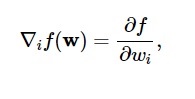
แหล่งที่มา

ที่นี่ i = 1,…..,n .

อนุพันธ์อันดับสองของฟังก์ชันการสูญเสียถูกจัดกลุ่มใน เมทริกซ์เฮสเซียน ดังนี้:

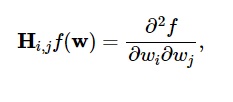
แหล่งที่มา

ที่นี่ i,j = 0,1,…

ตอนนี้เรารู้แล้วว่าปัญหาการเรียนรู้คืออะไร เราสามารถหารือเกี่ยวกับห้าหลัก

อัลกอริธึมโครงข่ายประสาทเทียม

1. การเพิ่มประสิทธิภาพหนึ่งมิติ

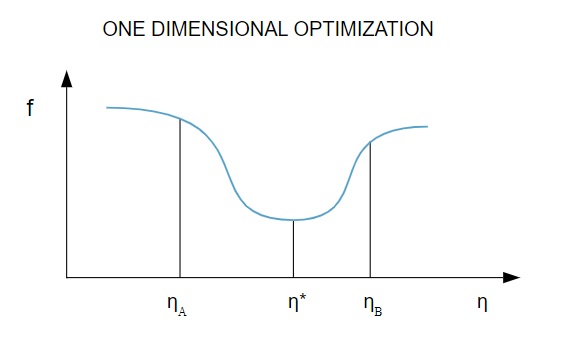
เนื่องจาก ฟังก์ชันการสูญเสีย ขึ้นอยู่กับพารามิเตอร์หลายตัว วิธีการปรับให้เหมาะสมแบบหนึ่งมิติจึงเป็นเครื่องมือในการฝึกอบรม Neural Network ขั้นแรก อัลกอริธึมการฝึกอบรมจะคำนวณทิศทางการฝึก ( d ) จากนั้นจึงคำนวณอัตราการฝึก ( η ) ที่ช่วยลดการสูญเสียในทิศทางการฝึก [ f(η) ]

แหล่งที่มา

ในแผนภาพ จุด η1 และ η2 กำหนดช่วงเวลาที่มีค่าต่ำสุดของ f, η *

ดังนั้น วิธีการเพิ่มประสิทธิภาพแบบหนึ่งมิติจึงมุ่งที่จะหาค่าต่ำสุดของฟังก์ชันหนึ่งมิติที่กำหนด อัลกอริธึมหนึ่งมิติที่ใช้กันมากที่สุด 2 วิธีคือ Golden Section Method และ Brent's Method

วิธีมาตราทอง

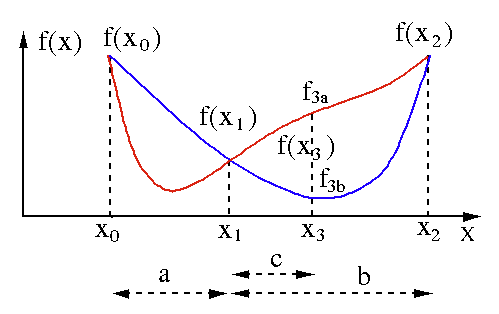
อัลกอริธึมการค้นหาส่วนสีทองใช้เพื่อค้นหาค่าต่ำสุดหรือสูงสุดของฟังก์ชันตัวแปรเดียว [ f(x) ] หากเรารู้อยู่แล้วว่าฟังก์ชันมีค่าต่ำสุดระหว่างจุดสองจุด เราก็สามารถทำการค้นหาซ้ำได้เหมือนกับที่ทำในการค้นหารากของสมการแบบสองส่วน f (x) = 0 นอกจากนี้ หากเราสามารถหาจุดสามจุด ( x0 < x1 < x2 ) ที่สอดคล้องกับ f(x0) > f(x1) > f(X2) ในย่านค่าต่ำสุด เราก็สามารถสรุปได้ว่าค่าต่ำสุดอยู่ระหว่าง x0 และ x2 . เพื่อหาค่าต่ำสุดนี้ เราสามารถพิจารณาอีกจุด x3 ระหว่าง x1 และ x2 ซึ่งจะให้ผลลัพธ์ต่อไปนี้แก่เรา:

• ถ้า f(x3) = f3a > f(x1) ค่าต่ำสุดอยู่ภายในช่วง x3 – x0 = a + c ที่เกี่ยวข้องกับจุดใหม่สามจุด x0 < x1 < x3 (ที่นี่ x2 ถูกแทนที่ด้วย x3 )
• ถ้า f(x3) = f3b > f(x1 ) ค่าต่ำสุดอยู่ภายในช่วงเวลา x2 – x1 = b ที่เกี่ยวข้องกับจุดใหม่สามจุด x1 < x3 < x2 (ที่นี่ x0 ถูกแทนที่ด้วย x1 )

แหล่งที่มา

วิธีการของเบรนท์

วิธีการของเบรนต์คืออัลกอริธึมการค้นหารากที่รวม การ ถ่ายคร่อมราก การ แบ่ง สองส่วน ซี แคน ต์ และ การแก้ไขกำลังสอง แบบ ผกผัน แม้ว่าอัลกอริธึมนี้จะพยายามใช้วิธีซีแคนต์ที่บรรจบกันอย่างรวดเร็วหรือการแก้ไขกำลังสองแบบผกผันทุกครั้งที่ทำได้ แต่ก็มักจะเปลี่ยนกลับเป็นวิธีการสองส่วน ดำเนินการใน ภาษา Wolfram วิธีการของ Brent แสดงเป็น:

วิธีการ -> Brent ใน FindRoot [eqn, x, x0, x1]

ในวิธีการของ Brent เราใช้ Lagrange interpolating polynomial ของดีกรี 2 ในปี 1973 Brent อ้างว่าวิธีนี้จะบรรจบกันเสมอ หากค่าของฟังก์ชันสามารถคำนวณได้ภายในขอบเขตเฉพาะ ซึ่งรวมถึงรูทด้วย หากมีสามจุด x1, x2 และ x3 วิธีของเบรนต์จะพอดีกับ x เป็นฟังก์ชันกำลังสองของ y โดยใช้สูตรการประมาณค่า:

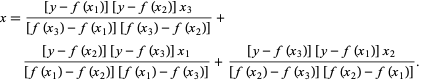
แหล่งที่มา

การประมาณการรูตที่ตามมาทำได้โดยการพิจารณา ดังนั้นจึงสร้างสมการต่อไปนี้:

แหล่งที่มา

โดยที่ P = S [ T(R – T) (x3 – x2) – (1 – R) (x2 -x1) ] และ Q = (T – 1) (R – 1) (S – 1) และ

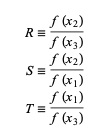
แหล่งที่มา

2. การเพิ่มประสิทธิภาพหลายมิติ

ถึงตอนนี้ เรารู้แล้วว่าปัญหาการเรียนรู้ของ Neural Networks มีเป้าหมายเพื่อค้นหาเวกเตอร์พารามิเตอร์ ( w* ) ซึ่งฟังก์ชันการสูญเสีย ( f ) ใช้ค่าต่ำสุด ตามข้อบังคับของเงื่อนไขมาตรฐาน หาก Neural Network มีฟังก์ชันการสูญเสียน้อยที่สุด การไล่ระดับสีจะเป็นเวกเตอร์ศูนย์

เนื่องจากฟังก์ชันการสูญเสียเป็นฟังก์ชันที่ไม่เป็นเชิงเส้นของพารามิเตอร์ จึงเป็นไปไม่ได้ที่จะหาอัลกอริธึมการฝึกอบรมแบบปิดเป็นค่าน้อยที่สุด อย่างไรก็ตาม หากเราพิจารณาค้นหาผ่านช่องว่างพารามิเตอร์ที่มีชุดของขั้นตอน ในแต่ละขั้นตอน ความสูญเสียจะลดลงโดยการปรับพารามิเตอร์ของโครงข่ายประสาทเทียม

ในการเพิ่มประสิทธิภาพหลายมิติ Neural Network จะได้รับการฝึกอบรมโดยการเลือกเวกเตอร์พารามิเตอร์แบบสุ่ม จากนั้นจึงสร้างลำดับของพารามิเตอร์เพื่อให้แน่ใจว่าฟังก์ชันการสูญเสียจะลดลงตามการวนซ้ำของอัลกอริทึมแต่ละครั้ง ความผันแปรของการสูญเสียระหว่างสองขั้นตอนต่อมาเรียกว่า “การสูญเสียการสูญเสีย” กระบวนการลดการสูญเสียจะดำเนินต่อไปจนกว่าอัลกอริธึมการฝึกอบรมจะไปถึงหรือเป็นไปตามเงื่อนไขที่ระบุ

ต่อไปนี้คือตัวอย่างสามตัวอย่างของอัลกอริธึมการปรับให้เหมาะสมหลายมิติ:

การไล่ระดับสีโคตร

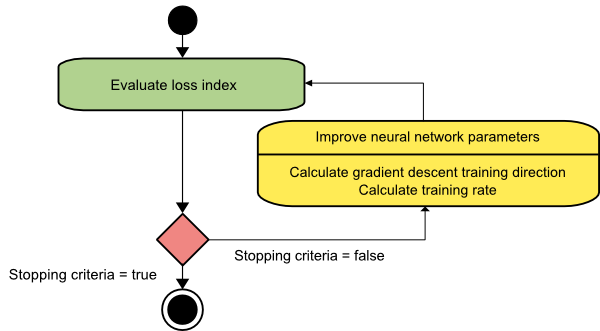
อัลกอริทึมการไล่ระดับสีแบบเกรเดียนท์น่าจะเป็นอัลกอริธึมการฝึกอบรมที่ง่ายที่สุด เนื่องจากอาศัยข้อมูลที่ให้ไว้ `จากเวกเตอร์การไล่ระดับสี มันเป็นวิธีการลำดับแรก ในวิธีนี้ เราจะใช้ f[w(i)] = f(i) และ ∇f[w(i)] = g(i ) จุดเริ่มต้นของอัลกอริธึมการฝึกอบรมนี้คือ w(0) ที่จะดำเนินต่อไปจนกว่าจะเป็นไปตามเกณฑ์ที่กำหนด โดยจะย้ายจาก w(i) เป็น w(i+1) ไปในทิศทางการฝึก d(i) = −g(i) . ดังนั้นการไล่ระดับการไล่ระดับสีจะวนซ้ำดังนี้:

w(i+1) = w(i)−g(i)η(i),

ที่นี่ i = 0,1,…

พารามิเตอร์ η แสดงถึงอัตราการฝึกอบรม คุณสามารถตั้งค่าคงที่สำหรับ η หรือตั้งค่าเป็นค่าที่พบโดยการปรับให้เหมาะสมแบบหนึ่งมิติตามทิศทางการฝึกในทุกขั้นตอน อย่างไรก็ตาม ขอแนะนำให้ตั้งค่าที่เหมาะสมที่สุดสำหรับอัตราการฝึกอบรมที่ทำได้โดยการลดบรรทัดให้เหลือน้อยที่สุดในแต่ละขั้นตอน

แหล่งที่มา

อัลกอริธึมนี้มีข้อจำกัดมากมาย เนื่องจากต้องมีการทำซ้ำหลายครั้งสำหรับฟังก์ชันที่มีโครงสร้างหุบเขาที่ยาวและแคบ แม้ว่าฟังก์ชันการสูญเสียจะลดลงอย่างรวดเร็วที่สุดในทิศทางของการไล่ระดับลงเนิน แต่ก็ไม่ได้รับประกันว่าจะมีการบรรจบกันเร็วที่สุดเสมอไป

วิธีการของนิวตัน

นี่เป็นอัลกอริธึมอันดับสองเนื่องจากใช้เมทริกซ์เฮสเซียน วิธีการของนิวตันมีจุดมุ่งหมายเพื่อค้นหาทิศทางการฝึกอบรมที่ดีขึ้นโดยใช้อนุพันธ์อันดับสองของฟังก์ชันการสูญเสีย ที่นี่เราจะแสดงว่า f[w(i)] = f(i), ∇f[w(i)]=g(i) และ Hf[w(i)] = H(i ) ตอนนี้ เราจะพิจารณาการประมาณกำลังสองของ f ที่ w(0) โดยใช้การขยายอนุกรมของเทย์เลอร์ ดังนี้:

f = f(0)+g(0)⋅[w−w(0)] + 0.5⋅[w−w(0)]2⋅H(0)

ที่นี่ H(0) คือเมทริกซ์ Hessian ของ f ที่คำนวณ ณ จุด w(0 ) เมื่อพิจารณา g = 0 สำหรับค่าต่ำสุดของ f(w) เราจะได้สมการต่อไปนี้:

g = g(0)+H(0)⋅(w−w(0))=0

จากผลที่ได้ เราจะเห็นได้ว่าเริ่มต้นจากเวกเตอร์พารามิเตอร์ w(0) วิธีการของนิวตันจะวนซ้ำดังนี้:

w(i+1) = w(i)−H(i)-1⋅g(i)

ที่นี่ i = 0,1 ,… และเวกเตอร์ H(i)−1⋅g(i) เรียกว่า "Newton's Step" คุณต้องจำไว้ว่าการเปลี่ยนแปลงพารามิเตอร์อาจเคลื่อนไปสู่ค่าสูงสุดแทนที่จะไปในทิศทางที่น้อยที่สุด โดยปกติ สิ่งนี้จะเกิดขึ้นหากเมทริกซ์เฮสเซียนไม่ชัดเจนในเชิงบวก ซึ่งจะทำให้การประเมินฟังก์ชันลดลงในการวนซ้ำแต่ละครั้ง อย่างไรก็ตาม เพื่อหลีกเลี่ยงปัญหานี้ เรามักจะแก้ไขสมการวิธีการดังนี้:

w(i+1) = w(i)−(H(i)-1⋅g(i))η

ที่นี่ ผม = 0,1 ,….

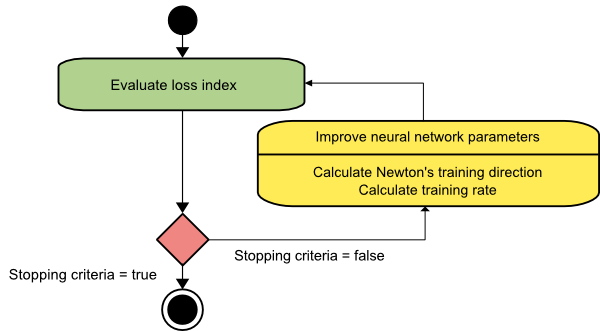
คุณสามารถกำหนดอัตราการฝึกอบรม η เป็นค่าคงที่หรือค่าที่ได้รับผ่านการย่อขนาดบรรทัด ดังนั้น เวกเตอร์ d(i)=H(i)-1⋅g(i) จึงกลายเป็นทิศทางการฝึกสำหรับวิธีของนิวตัน

แหล่งที่มา

ข้อเสียเปรียบที่สำคัญของวิธีการของนิวตันคือการประเมิน Hessian ที่แน่นอนและการผกผันนั้นเป็นการคำนวณที่ค่อนข้างแพง

คอนจูเกตไล่ระดับ

วิธีการเกรเดียนต์ของคอนจูเกตอยู่ระหว่างการเกรเดียนท์โคตรและวิธีของนิวตัน มันเป็นอัลกอริธึมระดับกลาง – ในขณะที่มีจุดมุ่งหมายเพื่อเร่งปัจจัยการบรรจบกันที่ช้าของวิธีการเกรเดียนท์ descent มันยังขจัดความจำเป็นสำหรับข้อกำหนดด้านข้อมูลที่เกี่ยวข้องกับการประเมิน การจัดเก็บ และการผกผันของเมทริกซ์เฮสเซียนที่มักจะต้องใช้ในวิธีของนิวตัน

อัลกอริธึมการไล่ระดับสีคอนจูเกตทำการค้นหาในทิศทางคอนจูเกตที่ให้การบรรจบกันเร็วกว่าทิศทางการไล่ระดับสี ทิศทางการฝึกอบรมเหล่านี้จะผันตามเมทริกซ์เฮสเซียน ในที่นี้ d หมายถึงเวกเตอร์ทิศทางการฝึก ถ้าเราเริ่มต้นด้วยเวกเตอร์พารามิเตอร์เริ่มต้น [w(0)] และเวกเตอร์ทิศทางการฝึกเริ่มต้น [d(0)=−g(0)] วิธีการไล่ระดับคอนจูเกตจะสร้างลำดับของทิศทางการฝึกอบรมที่แสดงเป็น:

d(i+1) = ก.(i+1)+d(i)⋅γ(i),

ที่นี่ i = 0,1 ,… และ γ เป็นพารามิเตอร์คอนจูเกต ทิศทางการฝึกสำหรับ อัลกอริธึมการไล่ระดับสีคอนจูเกต ทั้งหมด จะถูกรีเซ็ตเป็นระยะเป็นค่าลบของการไล่ระดับสี พารามิเตอร์ได้รับการปรับปรุง และอัตราการฝึกอบรม ( η ) ทำได้โดยการลดบรรทัดให้น้อยที่สุด ตามนิพจน์ที่แสดงด้านล่าง:

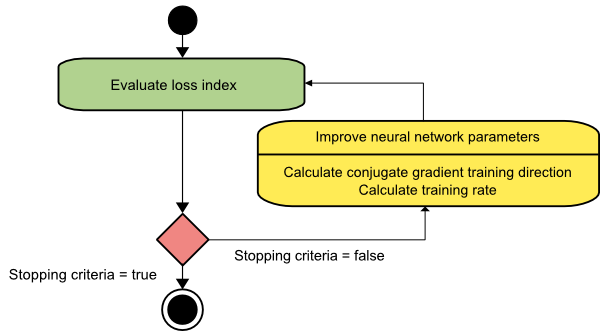
w(i+1) = w(i)+d(i)⋅η(i)

ที่นี่ i = 0,1 ,…

แหล่งที่มา

บทสรุป

แต่ละอัลกอริธึมมาพร้อมกับข้อดีและข้อเสียที่ไม่เหมือนใคร นี่เป็นเพียงไม่กี่อัลกอริธึมที่ใช้ในการฝึก Neural Networks และหน้าที่ของพวกมันแสดงให้เห็นเพียงส่วนปลายของภูเขาน้ำแข็ง – เมื่อ เฟรมเวิร์ก Deep Learning พัฒนาขึ้น ฟังก์ชันการทำงานของอัลกอริธึมเหล่านี้ก็เช่นกัน

หากคุณสนใจที่จะเรียนรู้เพิ่มเติมเกี่ยวกับโครงข่ายประสาทเทียม โปรแกรมแมชชีนเลิร์นนิง & AI ลองดู โปรแกรม Executive PG ของ IIIT-B & upGrad ในการเรียนรู้ของเครื่องและ AI ซึ่งออกแบบมาสำหรับมืออาชีพที่ทำงานและมีการฝึกอบรมที่เข้มงวดมากกว่า 450 ชั่วโมง 30+ กรณีศึกษาและการมอบหมายงาน, สถานะศิษย์เก่า IIIT-B, โครงการหลักที่ปฏิบัติได้จริงมากกว่า 5 โครงการและความช่วยเหลือด้านงานกับบริษัทชั้นนำ