ニューラルネットワーク：アーキテクチャ、コンポーネント、トップアルゴリズム

人工ニューラルネットワーク（ANN）は、ディープラーニングプロセスの不可欠な部分を構成します。 それらは人間の脳の神経学的構造に触発されています。 AILabPageによると、ANNは、「人間の脳の動作および処理データ（情報）モデルをシミュレートするための人間の生物学的脳構造に触発された、多数の単純で高度に相互接続された処理要素で記述された複雑なコンピューターコード」です。

世界のトップ大学（修士、エグゼクティブ大学院プログラム、ML＆AIの高度な証明書プログラム）からオンラインで最高の機械学習認定に参加して、キャリアを早急に進めましょう。

ディープラーニングは、次の5つのコアニューラルネットワークに焦点を当てています。

• 多層パーセプトロン
• 動径基底ネットワーク
• リカレントニューラルネットワーク
• 生成的敵対的ネットワーク
• 畳み込みニューラルネットワーク。

ニューラルネットワーク：アーキテクチャ

ニューラルネットワークは、複数の入力を取り込んで単一の出力を生成できる人工ニューロンで作られた複雑な構造です。 これはニューラルネットワークの主な仕事であり、入力を意味のある出力に変換します。 通常、ニューラルネットワークは、1つまたは複数の隠れ層を含む入力層と出力層で構成されます。

ニューラルネットワークでは、すべてのニューロンが相互に影響を及ぼし合うため、すべてのニューロンが接続されます。 ネットワークは、手元にあるデータセットのあらゆる側面と、データのさまざまな部分が互いにどのように関連しているかどうかを確認して監視できます。 これが、ニューラルネットワークが膨大な量のデータから非常に複雑なパターンを見つけることができる方法です。

読む：機械学習とニューラルネットワーク

ニューラルネットワークでは、情報の流れは2つの方法で発生します–

• フィードフォワードネットワーク：このモデルでは、信号は出力層に向かって一方向にのみ移動します。 フィードフォワードネットワークには、入力層と、ゼロまたは複数の隠れ層を持つ単一の出力層があります。 それらはパターン認識で広く使用されています。
• フィードバックネットワーク：このモデルでは、反復ネットワークまたは対話型ネットワークは、内部状態（メモリ）を使用して入力のシーケンスを処理します。 それらでは、信号はネットワーク内のループ（隠れ層）を介して両方向に移動できます。 これらは通常、時系列および順次タスクで使用されます。

ニューラルネットワーク：コンポーネント

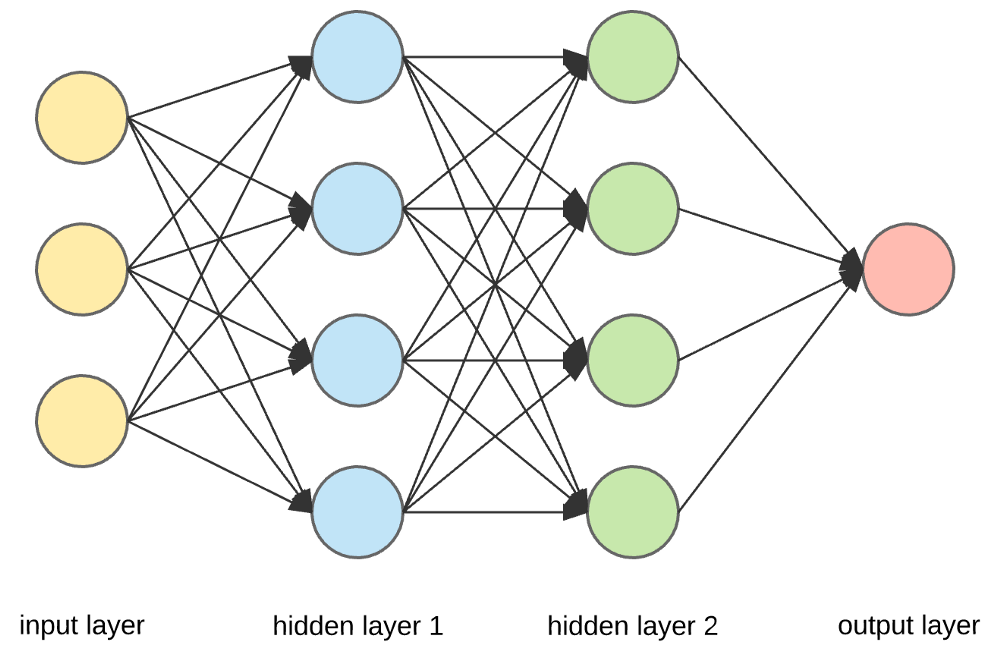
ソース

入力層、ニューロン、および重み–

上の図では、最も外側の黄色のレイヤーが入力レイヤーです。 ニューロンはニューラルネットワークの基本単位です。 それらは、外部ソースまたは他のノードから入力を受け取ります。 各ノードは次のレイヤーの別のノードに接続されており、そのような接続にはそれぞれ特定の重みがあります。 重みは、他の入力に対する相対的な重要性に基づいてニューロンに割り当てられます。

黄色のレイヤーのすべてのノード値が（それらの重みとともに）乗算されて要約されると、最初の非表示レイヤーの値が生成されます。 要約された値に基づいて、青いレイヤーには、このノードが「アクティブ化」されるかどうか、およびどの程度「アクティブ化」されるかを決定する事前定義された「アクティブ化」機能があります。

お茶を作るという簡単な日常の仕事を使ってこれを理解しましょう。 製茶工程では、茶の原料（水、茶葉、牛乳、砂糖、香辛料）が起点となる「ニューロン」です。 各成分の量は「重量」を表しています。 茶葉を水に入れ、砂糖、香辛料、牛乳を鍋に入れると、すべての材料が混ざり合って別の状態に変わります。 この変換プロセスは、「活性化関数」を表しています。

について学ぶ：ディープラーニングとニューラルネットワーク

隠しレイヤーと出力レイヤー–

入力レイヤーと出力レイヤーの間に隠された1つまたは複数のレイヤーは、隠しレイヤーと呼ばれます。 それは常に外界から隠されているので、それは隠された層と呼ばれます。 ニューラルネットワークの主な計算は、隠れ層で行われます。 したがって、隠れ層は入力層からすべての入力を受け取り、結果を生成するために必要な計算を実行します。 次に、この結果は出力レイヤーに転送され、ユーザーは計算結果を表示できます。

私たちのお茶作りの例では、すべての材料を混ぜると、加熱すると配合の状態と色が変わります。 材料は隠された層を表しています。 ここで、加熱は最終的に結果をもたらす活性化プロセス、つまりお茶を表しています。

ニューラルネットワーク：アルゴリズム

ニューラルネットワークでは、学習（またはトレーニング）プロセスは、データを3つの異なるセットに分割することによって開始されます。

• トレーニングデータセット–このデータセットにより、ニューラルネットワークはノード間の重みを理解できます。
• 検証データセット–このデータセットは、ニューラルネットワークのパフォーマンスを微調整するために使用されます。
• テストデータセット–このデータセットは、ニューラルネットワークの精度と許容誤差を決定するために使用されます。

データがこれらの3つの部分にセグメント化されると、ニューラルネットワークアルゴリズムがそれらに適用され、ニューラルネットワークがトレーニングされます。 ニューラルネットワークでトレーニングプロセスを促進するために使用される手順は最適化と呼ばれ、使用されるアルゴリズムはオプティマイザーと呼ばれます。 最適化アルゴリズムにはさまざまな種類があり、それぞれに固有の特性と、メモリ要件、数値精度、処理速度などの側面があります。

さまざまなニューラルネットワークアルゴリズムの説明に入る前に、まず学習の問題を理解しましょう。

また読む：実世界のニューラルネットワークアプリケーション

学習の問題とは何ですか？

損失指数（ f ）の最小化の観点から学習問題を表します。 ここで、「 f 」は、特定のデータセットでニューラルネットワークのパフォーマンスを測定する関数です。 一般に、損失指数は誤差項と正則化項で構成されます。 エラー項はニューラルネットワークがデータセットにどのように適合するかを評価しますが、正則化項はニューラルネットワークの効果的な複雑さを制御することによって過剰適合の問題を防ぐのに役立ちます。

損失関数[ f（w ]は、ニューラルネットワークの適応パラメーター（重みとバイアス）に依存します。これらのパラメーターは、単一のn次元重みベクトル（ w ）にグループ化できます。

損失関数の図解は次のとおりです。

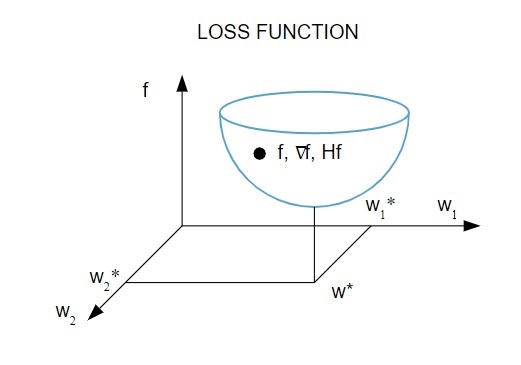
ソース

この図によると、損失関数の最小値は点（ w * ）で発生します。 いつでも、損失関数の1次および2次導関数を計算できます。 一次導関数は勾配ベクトルにグループ化され、その成分は次のように表されます。

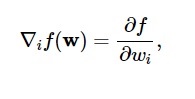
ソース

ここで、 i = 1、…..、n 。

損失関数の2次導関数は、次のようにヘッセ行列にグループ化されます。

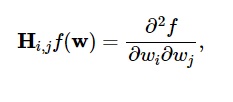
ソース

ここで、 i、j = 0,1、…

学習の問題が何であるかがわかったので、5つの主要な問題について話し合うことができます。

ニューラルネットワークアルゴリズム。

1.1次元の最適化

損失関数は複数のパラメーターに依存するため、1次元の最適化手法はニューラルネットワークのトレーニングに役立ちます。 トレーニングアルゴリズムは、最初にトレーニング方向（ d ）を計算し、次にトレーニング方向の損失を最小限に抑えるのに役立つトレーニングレート（ η ）を計算します[ f（η） ]。

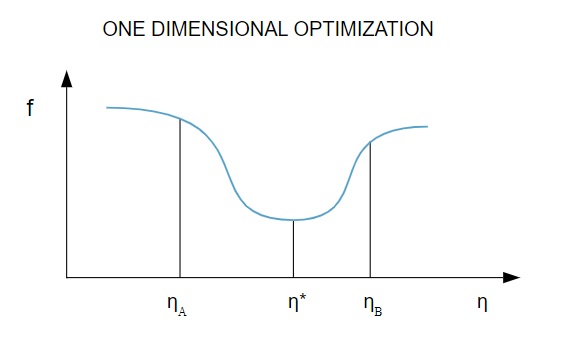
ソース

この図では、点η1とη2はfの最小値η*を含む区間を定義しています。

したがって、1次元最適化手法は、特定の1次元関数の最小値を見つけることを目的としています。 最も一般的に使用される1次元アルゴリズムの2つは、黄金分割法とブレント法です。

黄金分割法

黄金分割探索アルゴリズムは、単一変数関数[ f（x） ]の最小値または最大値を見つけるために使用されます。 関数が2点の間に最小値を持っていることがすでにわかっている場合は、方程式f（x）= 0の根を二分法で検索する場合と同じように、反復検索を実行できます。 また、最小値の近傍にf（x0）> f（x1）> f（X2）に対応する3つの点（ x0 <x1 <x2 ）が見つかった場合、最小値がx0とx2の間に存在すると推定できます。 。 この最小値を見つけるために、 x1とx2の間の別の点x3を検討できます。これにより、次の結果が得られます。

• f （x3）= f3a> f（x1）の場合、最小値は3つの新しい点x0 <x1 <x3に関連する区間x3– x0 = a + c内にあります（ここでx2はx3に置き換えられます）。
• f （x3）= f3b> f（x1 ）の場合、最小値は3つの新しい点x1 <x3 <x2に関連する区間x2– x1 = b内にあります（ここでx0はx1に置き換えられます）。

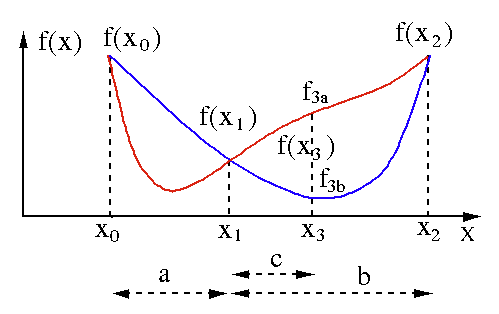
ソース

ブレント法

ブレント法は、ルートブラケット、二分法、割線、および逆二次補間を組み合わせた求根アルゴリズムです。 このアルゴリズムは、可能な限り高速収束割線法または逆二分法を使用しようとしますが、通常は二分法に戻ります。 Wolfram言語で実装されたブレント法は次のように表されます。

メソッド-> FindRootのブレント[eqn、x、x0、x1]。

ブレント法では、次数2のラグランジュ補間多項式を使用します。1973年、ブレントは、関数の値がルートを含む特定の領域内で計算可能であれば、この方法は常に収束すると主張しました。 3つの点x1、x2、およびx3がある場合、ブレント法は、内挿式を使用して、 xをyの2次関数として近似します。

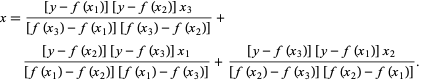
ソース

後続のルート推定は、を考慮して達成され、それによって次の方程式が生成されます。

ソース

ここで、 P = S [T（R – T）（x3 – x2）–（1 – R）（x2 -x1）]およびQ =（T – 1）（R – 1）（S – 1）および、

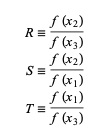
ソース

2.多次元最適化

これまでに、ニューラルネットワークの学習問題は、損失関数（ f ）が最小値をとるパラメーターベクトル（ w * ）を見つけることを目的としていることをすでに知っています。 標準状態の義務によれば、ニューラルネットワークが損失関数の最小値である場合、勾配はゼロベクトルです。

損失関数はパラメーターの非線形関数であるため、最小値のクローズドトレーニングアルゴリズムを見つけることは不可能です。 ただし、一連のステップを含むパラメーター空間を検索することを検討すると、各ステップで、ニューラルネットワークのパラメーターを調整することで損失が減少します。

多次元最適化では、ランダムなweパラメーターベクトルを選択し、パラメーターのシーケンスを生成して、アルゴリズムの反復ごとに損失関数が減少するようにすることで、ニューラルネットワークをトレーニングします。 後続の2つのステップ間のこの損失の変動は、「損失の減少」として知られています。 損失の減少プロセスは、トレーニングアルゴリズムが指定された条件に達するか、それを満たすまで続きます。

多次元最適化アルゴリズムの3つの例を次に示します。

最急降下法

最急降下アルゴリズムは、おそらくすべてのトレーニングアルゴリズムの中で最も単純です。 勾配ベクトルから提供される情報に依存しているため、1次の方法です。 この方法では、 f [w（i）] = f（i）および∇f[w（i）] = g（i）を取ります。 このトレーニングアルゴリズムの開始点はw（0）であり、指定された基準が満たされるまで進行し続けます。トレーニング方向d（i）= −g（i）でw（i）からw（i + 1）に移動します。 。 したがって、最急降下法は次のように繰り返されます。

w（i + 1）= w（i）−g（i）η（i）、

ここで、 i = 0,1、…

パラメータηはトレーニング率を表します。 ηに固定値を設定することも、すべてのステップでトレーニング方向に沿って1次元最適化によって検出された値に設定することもできます。 ただし、各ステップでのライン最小化によって達成されるトレーニング率の最適値を設定することをお勧めします。

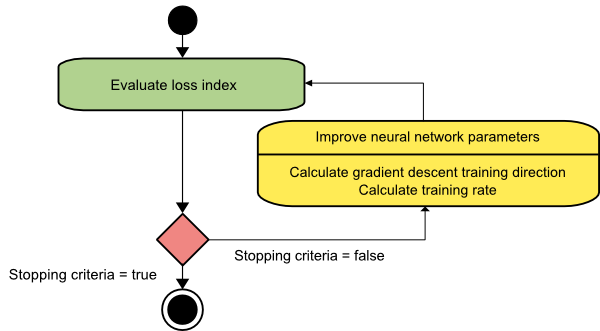
ソース

このアルゴリズムには、長くて狭い谷の構造を持つ関数に対して多数の反復が必要になるため、多くの制限があります。 損失関数は下り坂の勾配の方向に最も急速に減少しますが、常に最速の収束を保証するわけではありません。

ニュートン法

これは、ヘッセ行列を利用するため、2次アルゴリズムです。 ニュートン法は、損失関数の2次導関数を利用することにより、より良いトレーニングの方向性を見つけることを目的としています。 ここでは、 f [w（i）] = f（i）、∇f[w（i）] = g（i） 、およびHf [w（i）] = H（i）と表記します。 ここで、テイラー級数展開を使用して、 w（0）でのfの2次近似を次のように検討します。

f = f（0）+ g（0）⋅[w−w（0）] +0.5⋅[w−w（0）]2⋅H（0）

ここで、 H（0）は、点w（0）で計算されたfのヘッセ行列です。 f（w）の最小値としてg = 0を考慮すると、次の式が得られます。

g = g（0）+ H（0）⋅（w−w（0））= 0

その結果、パラメーターベクトルw（0）から開始して、ニュートン法は次のように繰り返されることがわかります。

w（i + 1）= w（i）−H（i）−1⋅g（i）

ここで、 i = 0,1 、…であり、ベクトルH（i）−1⋅g（i）は「ニュートンのステップ」と呼ばれます。 パラメータの変更は、最小の方向ではなく、最大の方向に移動する可能性があることを覚えておく必要があります。 通常、これはヘッセ行列が正定値でない場合に発生し、それによって各反復で関数評価が減少します。 ただし、この問題を回避するために、通常、メソッドの式を次のように変更します。

w（i + 1）= w（i）−（H（i）−1⋅g（i））η

ここで、 i = 0,1 、…。

トレーニングレートηを固定値またはライン最小化によって取得された値に設定できます。 したがって、ベクトルd（i）= H（i）-1⋅g（i）がニュートン法のトレーニング方向になります。

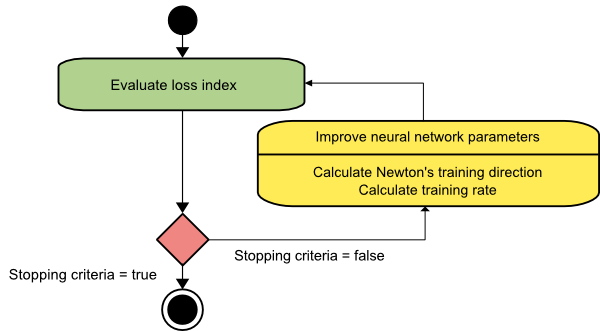
ソース

ニュートン法の主な欠点は、ヘッセ行列とその逆行列の正確な評価がかなり高価な計算になることです。

共役勾配

共役勾配法は、最急降下法とニュートン法の間にあります。 これは中間アルゴリズムです。最急降下法の遅い収束係数を加速することを目的としていますが、ニュートン法で通常必要とされるヘッセ行列の評価、保存、および反転に関する情報要件の必要性も排除します。

共役勾配トレーニングアルゴリズムは、勾配降下方向よりも高速な収束を実現する共役方向で検索を実行します。 これらのトレーニングの方向性は、ヘッセ行列に従って共役になっています。 ここで、dはトレーニング方向ベクトルを示します。 初期パラメーターベクトル[w（0）]と初期トレーニング方向ベクトル[d（0）=-g（0）]で開始する場合、共役勾配法は次のように表されるトレーニング方向のシーケンスを生成します。

d（i + 1）= g（i + 1）+ d（i）⋅γ（i）、

ここで、 i = 0,1 、…であり、γは共役パラメーターです。 すべての共役勾配アルゴリズムのトレーニング方向は、勾配の負の値に定期的にリセットされます。 以下に示す式に従って、パラメータが改善され、トレーニング率（ η ）がライン最小化によって達成されます。

w（i + 1）= w（i）+ d（i）⋅η（i）

ここで、 i = 0,1 、…

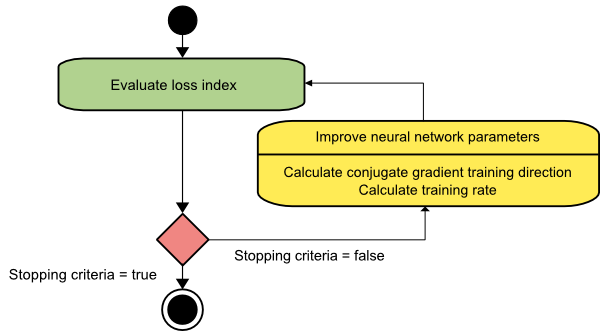
ソース

結論

各アルゴリズムには、固有の長所と短所があります。 これらはニューラルネットワークのトレーニングに使用されるアルゴリズムのほんの一部であり、それらの機能は氷山の一角を示すだけです。ディープラーニングフレームワークが進歩するにつれて、これらのアルゴリズムの機能も進歩します。

ニューラルネットワーク、機械学習プログラム、AIについて詳しく知りたい場合は、IIIT-BとupGradの機械学習とAIのエグゼクティブPGプログラムをご覧ください。これは、働く専門家向けに設計されており、450時間以上の厳格なトレーニングを30時間以上提供しています。ケーススタディと課題、IIIT-B卒業生のステータス、5つ以上の実践的なキャップストーンプロジェクト、トップ企業との仕事の支援。