Sieć neuronowa: architektura, komponenty i najlepsze algorytmy

Sztuczne sieci neuronowe (ANN) stanowią integralną część procesu Deep Learning. Inspirują się neurologiczną strukturą ludzkiego mózgu. Według AILabPage , SSN to „złożony kod komputerowy napisany z wieloma prostymi, wysoce wzajemnie powiązanymi elementami przetwarzającymi, które są inspirowane ludzką biologiczną strukturą mózgu do symulacji modeli pracy i przetwarzania danych (informacji) ludzkiego mózgu”.

Dołącz online do najlepszych certyfikatów uczenia maszynowego z najlepszych światowych uniwersytetów — studiów magisterskich, programów podyplomowych dla kadry kierowniczej i zaawansowanego programu certyfikacji w zakresie uczenia się maszynowego i sztucznej inteligencji, aby przyspieszyć swoją karierę.

Głębokie uczenie koncentruje się na pięciu podstawowych sieciach neuronowych, w tym:

• Perceptron wielowarstwowy
• Radialna sieć bazowa
• Rekurencyjne sieci neuronowe
• Sieci generatywnych przeciwników
• Konwolucyjne sieci neuronowe.

Sieć neuronowa: architektura

Sieci neuronowe to złożone struktury wykonane ze sztucznych neuronów, które mogą pobierać wiele sygnałów wejściowych, aby wytworzyć pojedynczy sygnał wyjściowy. To jest główne zadanie sieci neuronowej – przekształcenie danych wejściowych w sensowne dane wyjściowe. Zwykle sieć neuronowa składa się z warstwy wejściowej i wyjściowej z jedną lub wieloma ukrytymi warstwami.

W sieci neuronowej wszystkie neurony wpływają na siebie nawzajem, a zatem wszystkie są połączone. Sieć może potwierdzać i obserwować każdy aspekt zbioru danych oraz to, w jaki sposób różne części danych mogą, ale nie muszą, być ze sobą powiązane. W ten sposób sieci neuronowe są w stanie znaleźć niezwykle złożone wzorce w ogromnych ilościach danych.

Przeczytaj: Uczenie maszynowe a sieci neuronowe

W sieci neuronowej przepływ informacji odbywa się na dwa sposoby –

• Sieci sprzężenia zwrotnego: W tym modelu sygnały przemieszczają się tylko w jednym kierunku, w kierunku warstwy wyjściowej. Sieci feedforward mają warstwę wejściową i pojedynczą warstwę wyjściową z zerem lub wieloma ukrytymi warstwami. Są szeroko stosowane w rozpoznawaniu wzorców.
• Sieci sprzężenia zwrotnego: W tym modelu sieci rekurencyjne lub interaktywne wykorzystują swój stan wewnętrzny (pamięć) do przetwarzania sekwencji wejść. W nich sygnały mogą przemieszczać się w obu kierunkach przez pętle (warstwy ukryte) w sieci. Są one zwykle używane w zadaniach szeregowych i sekwencyjnych.

Sieć neuronowa: komponenty

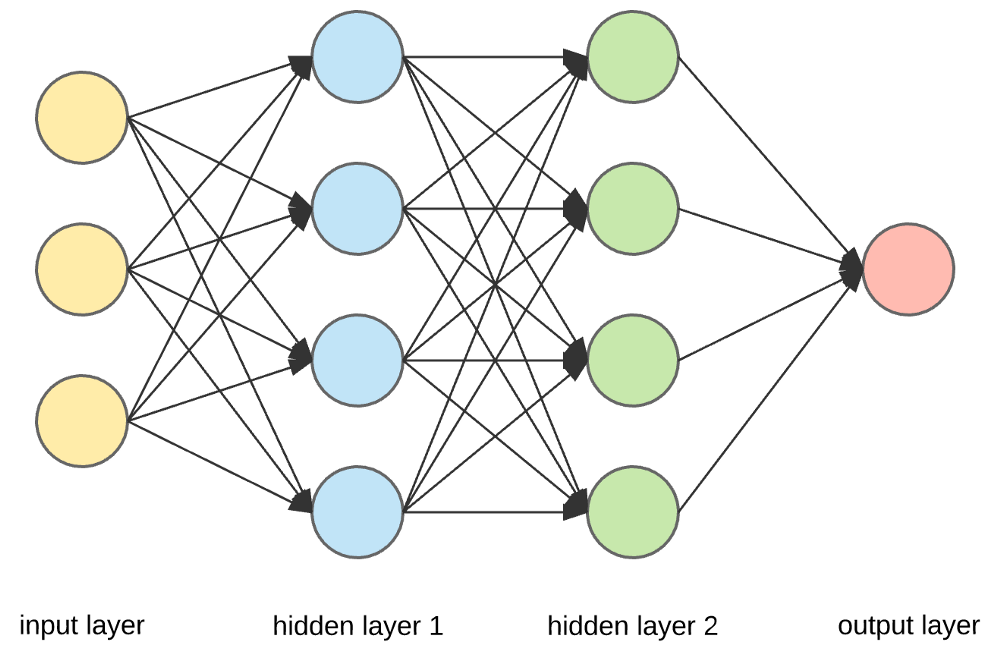
Źródło

Warstwy wejściowe, neurony i wagi —

Na powyższym rysunku najbardziej zewnętrzna warstwa żółta jest warstwą wejściową. Neuron to podstawowa jednostka sieci neuronowej. Otrzymują dane wejściowe z zewnętrznego źródła lub innych węzłów. Każdy węzeł jest połączony z innym węzłem z kolejnej warstwy, a każde takie połączenie ma określoną wagę. Wagi są przypisywane do neuronu na podstawie jego względnego znaczenia w stosunku do innych danych wejściowych.

Gdy wszystkie wartości węzłów z żółtej warstwy są pomnożone (wraz z ich wagą) i zsumowane, generuje wartość dla pierwszej ukrytej warstwy. Na podstawie sumarycznej wartości niebieska warstwa ma predefiniowaną funkcję „aktywacji”, która określa, czy ten węzeł będzie „aktywowany” i jak „aktywny” będzie.

Zrozummy to za pomocą prostego, codziennego zadania – robienia herbaty. W procesie przygotowywania herbaty składniki używane do jej przygotowania (woda, liście herbaty, mleko, cukier i przyprawy) są „neuronami”, ponieważ stanowią one punkty wyjścia procesu. Ilość każdego składnika reprezentuje „wagę”. Gdy włożysz liście herbaty do wody i dodasz cukier, przyprawy i mleko na patelnię, wszystkie składniki wymieszają się i przejdą w inny stan. Ten proces transformacji reprezentuje „funkcję aktywacji”.

Dowiedz się więcej o: Głębokie uczenie a sieci neuronowe

Warstwy ukryte i warstwa wyjściowa —

Warstwa lub warstwy ukryte między warstwą wejściową a wyjściową są nazywane warstwą ukrytą. Nazywa się to warstwą ukrytą, ponieważ zawsze jest ukryta przed światem zewnętrznym. Główne obliczenia sieci neuronowej odbywają się w warstwach ukrytych. Tak więc warstwa ukryta pobiera wszystkie dane wejściowe z warstwy wejściowej i wykonuje niezbędne obliczenia, aby wygenerować wynik. Wynik ten jest następnie przekazywany do warstwy wyjściowej, aby użytkownik mógł zobaczyć wynik obliczeń.

W naszym przykładzie z herbatą, gdy zmieszamy wszystkie składniki, preparat zmienia swój stan i kolor po podgrzaniu. Składniki reprezentują ukryte warstwy. Tutaj ogrzewanie reprezentuje proces aktywacji, który w końcu dostarcza rezultat – herbatę.

Sieć neuronowa: algorytmy

W sieci neuronowej proces uczenia się (lub uczenia) jest inicjowany przez podzielenie danych na trzy różne zestawy:

• Zestaw danych uczących — ten zestaw danych umożliwia sieci neuronowej zrozumienie wag między węzłami.
• Zestaw danych walidacji — ten zestaw danych służy do dostrajania wydajności sieci neuronowej.
• Testowy zestaw danych — ten zestaw danych służy do określenia dokładności i marginesu błędu sieci neuronowej.

Gdy dane zostaną podzielone na te trzy części, algorytmy sieci neuronowej są do nich stosowane w celu uczenia sieci neuronowej. Procedura wykorzystywana do usprawnienia procesu uczenia się w sieci neuronowej nazywana jest optymalizacją, a zastosowany algorytm nazywany jest optymalizatorem. Istnieją różne typy algorytmów optymalizacji, z których każdy ma swoje unikalne cechy i aspekty, takie jak wymagania dotyczące pamięci, precyzja numeryczna i szybkość przetwarzania.

Zanim zagłębimy się w dyskusję na temat różnych algorytmów sieci neuronowych , najpierw zrozummy problem uczenia się.

Przeczytaj także : Aplikacje sieci neuronowych w świecie rzeczywistym

Jaki jest problem w nauce?

Przedstawiamy problem uczenia się w kategoriach minimalizacji wskaźnika strat ( f ). Tutaj „ f ” jest funkcją, która mierzy wydajność sieci neuronowej na danym zbiorze danych. Ogólnie rzecz biorąc, wskaźnik strat składa się z warunku błędu i warunku regularyzacji. Podczas gdy termin błędu ocenia, w jaki sposób sieć neuronowa pasuje do zestawu danych, termin regularyzacji pomaga zapobiegać problemowi nadmiernego dopasowania, kontrolując efektywną złożoność sieci neuronowej.

Funkcja straty [ f(w ] zależy od parametrów adaptacyjnych – wag i błędów systematycznych – sieci neuronowej, które można zgrupować w jeden n-wymiarowy wektor wag ( w ).

Oto obrazowa reprezentacja funkcji straty:

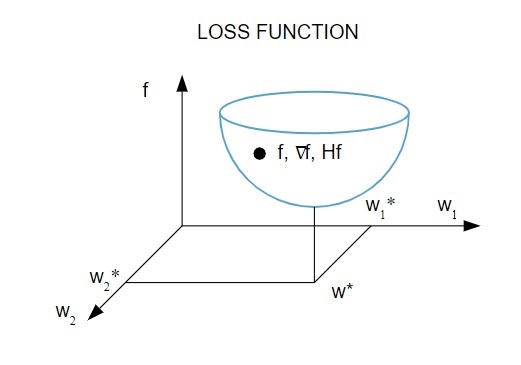
Źródło

Zgodnie z tym wykresem minimum funkcji straty występuje w punkcie ( w* ). W dowolnym momencie możesz obliczyć pierwszą i drugą pochodną funkcji straty. Pierwsze pochodne są zgrupowane w wektorze gradientowym, a jego składowe są przedstawione jako:

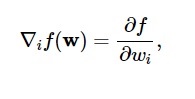
Źródło

Tutaj i = 1,…..,n .

Drugie pochodne funkcji straty są zgrupowane w macierzy Hess , tak jak:

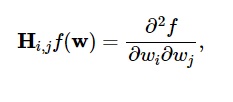
Źródło

Tutaj i,j = 0,1,…

Teraz, gdy wiemy, na czym polega problem z nauką, możemy omówić pięć głównych

Algorytmy sieci neuronowych .

1. Optymalizacja jednowymiarowa

Ponieważ funkcja strat zależy od wielu parametrów, metody optymalizacji jednowymiarowej są kluczowe w trenowaniu sieci neuronowych. Algorytmy treningowe najpierw obliczają kierunek treningu ( d ), a następnie obliczają wskaźnik treningu ( η ), który pomaga zminimalizować stratę w kierunku treningu [ f(η) ].

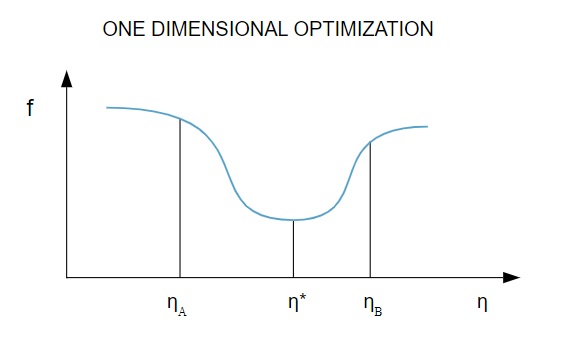
Źródło

Na wykresie punkty η1 i η2 definiują przedział zawierający minimum f, η* .

Zatem metody optymalizacji jednowymiarowej mają na celu znalezienie minimum danej funkcji jednowymiarowej. Dwa z najczęściej używanych algorytmów jednowymiarowych to metoda złotej sekcji i metoda Brenta.

Metoda złotej sekcji

Algorytm przeszukiwania złotej sekcji jest używany do znalezienia minimum lub maksimum funkcji jednej zmiennej [ f(x) ]. Jeśli już wiemy, że funkcja ma minimum między dwoma punktami, możemy przeprowadzić wyszukiwanie iteracyjne, tak jak w przypadku wyszukiwania bisekcji dla pierwiastka równania f(x) = 0 . Ponadto, jeśli możemy znaleźć trzy punkty ( x0 < x1 < x2 ) odpowiadające f(x0) > f(x1) > f(X2) w sąsiedztwie minimum, to możemy wywnioskować, że minimum istnieje między x0 a x2 . Aby znaleźć to minimum, możemy rozważyć kolejny punkt x3 pomiędzy x1 i x2 , który da nam następujące wyniki:

• Jeśli f(x3) = f3a > f(x1), minimum mieści się w przedziale x3 – x0 = a + c , który jest powiązany z trzema nowymi punktami x0 < x1 < x3 (tutaj x2 jest zastąpione przez x3 ).
• Jeśli f(x3) = f3b > f(x1 ), minimum mieści się w przedziale x2 – x1 = b w odniesieniu do trzech nowych punktów x1 < x3 < x2 (tutaj x0 jest zastąpione przez x1 ).

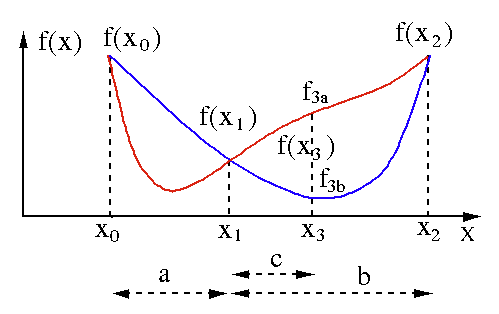
Źródło

Metoda Brenta

Metoda Brenta to algorytm wyszukiwania pierwiastków, który łączy w sobie nawiasy pierwiastkowe , bisekcję , sieczną i odwrotną interpolację kwadratową . Chociaż ten algorytm próbuje użyć metody siecznej szybko zbieżnej lub odwrotnej interpolacji kwadratowej, gdy tylko jest to możliwe, zwykle powraca do metody bisekcji. Zaimplementowana w języku Wolfram metoda Brenta jest wyrażona jako:

Metoda -> Brent w FindRoot [eqn, x, x0, x1].

W metodzie Brenta używamy wielomianu interpolującego Lagrange'a stopnia 2. W 1973 r. Brent twierdził, że ta metoda będzie zawsze zbieżna, pod warunkiem, że wartości funkcji są obliczalne w obrębie określonego regionu, w tym pierwiastka. Jeśli istnieją trzy punkty x1, x2 i x3 , metoda Brenta dopasowuje x jako funkcję kwadratową y , używając wzoru na interpolację:

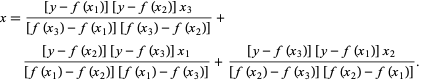
Źródło

Kolejne oszacowania pierwiastkowe uzyskuje się poprzez rozważenie, tworząc w ten sposób następujące równanie:

Źródło

Tutaj P = S [ T(R – T) (x3 – x2) – (1 – R) (x2 -x1) ] i Q = (T – 1) (R – 1) (S – 1) oraz,

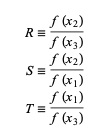
Źródło

2. Optymalizacja wielowymiarowa

Do tej pory wiemy już, że problem uczenia się sieci neuronowych ma na celu znalezienie wektora parametrów ( w* ), dla którego funkcja straty ( f ) przyjmuje minimalną wartość. Zgodnie z wymogami warunku standardowego, jeśli sieć neuronowa ma minimum funkcji straty, gradient jest wektorem zerowym.

Ponieważ funkcja straty jest nieliniową funkcją parametrów, niemożliwe jest znalezienie zamkniętych algorytmów uczących dla minimum. Jeśli jednak rozważymy przeszukanie przestrzeni parametrów, która zawiera serię kroków, na każdym kroku strata zostanie zmniejszona poprzez dostosowanie parametrów sieci neuronowej.

W optymalizacji wielowymiarowej sieć neuronowa jest szkolona poprzez wybranie losowego wektora parametrów we, a następnie wygenerowanie sekwencji parametrów, aby zapewnić, że funkcja straty maleje z każdą iteracją algorytmu. Ta odmiana straty pomiędzy dwoma kolejnymi krokami jest znana jako „zmniejszenie straty”. Proces zmniejszania strat trwa do momentu, gdy algorytm uczący osiągnie lub spełni określony warunek.

Oto trzy przykłady wielowymiarowych algorytmów optymalizacji:

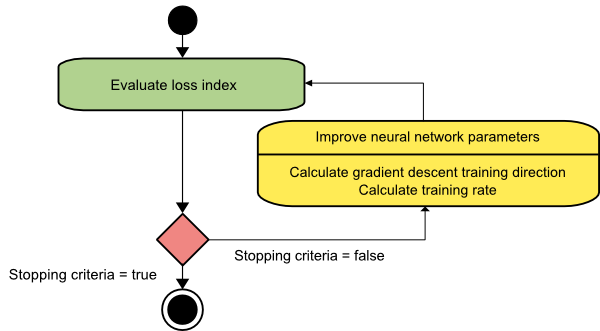
Zejście gradientowe

Algorytm zniżania gradientu jest prawdopodobnie najprostszym ze wszystkich algorytmów uczących. Ponieważ opiera się na informacjach dostarczonych z wektora gradientu, jest to metoda pierwszego rzędu. W tej metodzie przyjmiemy f[w(i)] = f(i) i ∇f[w(i)] = g(i) . Punktem wyjścia tego algorytmu uczącego jest w(0), które postępuje aż do spełnienia określonego kryterium – przesuwa się od w(i) do w(i+1) w kierunku uczenia d(i) = −g(i) . Stąd opadanie gradientu iteruje w następujący sposób:

w(i+1) = w(i)−g(i)η(i),

Tutaj ja = 0,1,…

Parametr η reprezentuje tempo treningu. Możesz ustawić stałą wartość dla η lub ustawić ją na wartość znalezioną przez optymalizację jednowymiarową wzdłuż kierunku treningu na każdym kroku. Jednak preferowane jest ustawienie optymalnej wartości tempa treningu osiągniętego przez minimalizację linii na każdym kroku.

Źródło

Algorytm ten ma wiele ograniczeń, ponieważ wymaga wielu iteracji dla funkcji o długich i wąskich strukturach dolin. Podczas gdy funkcja strat maleje najszybciej w kierunku spadku w dół, nie zawsze zapewnia najszybszą zbieżność.

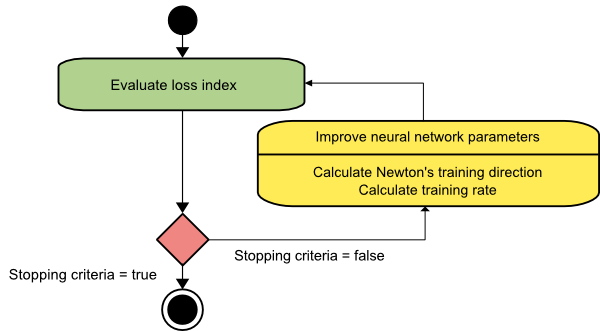
metoda Newtona

Jest to algorytm drugiego rzędu, ponieważ wykorzystuje macierz Hessian. Metoda Newtona ma na celu znalezienie lepszych kierunków treningu poprzez wykorzystanie drugiej pochodnej funkcji straty. Tutaj oznaczymy f[w(i)] = f(i), ∇f[w(i)]=g(i) i Hf[w(i)] = H(i) . Teraz rozważymy przybliżenie kwadratowe f przy w(0) przy użyciu rozwinięcia szeregów Taylora, tak jak poniżej:

f = f(0)+g(0)⋅[w−w(0)] + 0,5⋅[w−w(0)]2⋅H(0)

Tutaj H(0) jest macierzą Hessa f obliczoną w punkcie w(0) . Rozważając g = 0 jako minimum f(w) otrzymujemy następujące równanie:

g = g(0)+H(0)⋅(w−w(0))=0

W rezultacie widzimy, że zaczynając od wektora parametrów w(0), metoda Newtona iteruje w następujący sposób:

w(i+1) = w(i)−H(i)−1⋅g(i)

Tutaj i = 0,1 ,… a wektor H(i)−1⋅g(i) jest określany jako „krok Newtona”. Należy pamiętać, że zmiana parametrów może zmierzać w kierunku maksimum, a nie w kierunku minimum. Zwykle dzieje się tak, jeśli macierz Hessów nie jest dodatnio określona, ​​co powoduje, że ocena funkcji jest redukowana w każdej iteracji. Aby jednak uniknąć tego problemu, zwykle modyfikujemy równanie metody w następujący sposób:

w(i+1) = w(i)−(H(i)−1⋅g(i))η

Tutaj ja = 0,1 ,….

Możesz ustawić szybkość treningu η na stałą wartość lub wartość uzyskaną poprzez minimalizację linii. Zatem wektor d(i)=H(i)−1⋅g(i) staje się kierunkiem treningu dla metody Newtona.

Źródło

Główną wadą metody Newtona jest to, że dokładna ocena hesjanu i jego odwrotności są dość kosztownymi obliczeniami.

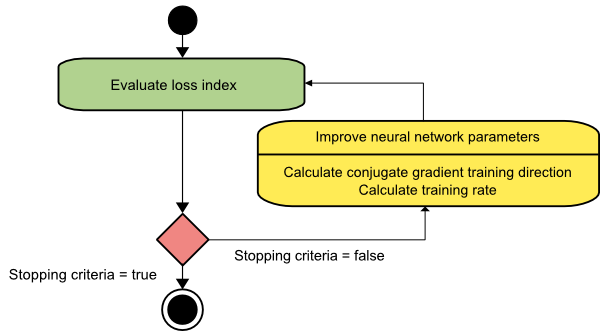
Gradient sprzężony

Metoda gradientu sprzężonego mieści się pomiędzy metodą gradientu opadania a metodą Newtona. Jest to algorytm pośredni – chociaż ma na celu przyspieszenie powolnego współczynnika zbieżności metody gradientu opadania, eliminuje również potrzebę wymagań informacyjnych dotyczących oceny, przechowywania i odwracania macierzy Hessów, zwykle wymaganych w metodzie Newtona.

Algorytm uczenia gradientu sprzężonego wykonuje wyszukiwanie w kierunkach sprzężonych, co zapewnia szybszą zbieżność niż kierunki opadania gradientu. Te kierunki treningowe są sprzężone zgodnie z macierzą Hesji. Tutaj d oznacza wektor kierunku treningu. Jeśli zaczniemy od początkowego wektora parametrów [w(0)] i początkowego wektora kierunku treningu [d(0)=−g(0)] , metoda gradientu sprzężonego generuje sekwencję kierunków treningu reprezentowaną jako:

d(i+1) = g(i+1)+d(i)⋅γ(i),

Tutaj i = 0,1 ,… a γ jest parametrem sprzężonym. Kierunek uczenia dla wszystkich sprzężonych algorytmów gradientu jest okresowo resetowany do wartości ujemnej gradientu. Parametry ulegają poprawie, a tempo treningu ( η ) osiąga się poprzez minimalizację linii, zgodnie z poniższym wyrażeniem:

w(i+1) = w(i)+d(i)⋅η(i)

Tutaj ja = 0,1 ,…

Źródło

Wniosek

Każdy algorytm ma unikalne zalety i wady. To tylko kilka algorytmów używanych do trenowania sieci neuronowych, a ich funkcje demonstrują jedynie wierzchołek góry lodowej – wraz z rozwojem frameworków Deep Learning , tak samo będzie z funkcjami tych algorytmów.

Jeśli chcesz dowiedzieć się więcej o sieciach neuronowych, programach uczenia maszynowego i sztucznej inteligencji , sprawdź program Executive PG w zakresie uczenia maszynowego i sztucznej inteligencji IIIT-B i upGrad, który jest przeznaczony dla pracujących profesjonalistów i oferuje ponad 450 godzin rygorystycznego szkolenia, ponad 30 studia przypadków i zadania, status absolwentów IIIT-B, ponad 5 praktycznych praktycznych projektów zwieńczenia i pomoc w pracy z najlepszymi firmami.