Rete neurale: architettura, componenti e algoritmi principali

Le reti neurali artificiali (ANN) costituiscono parte integrante del processo di Deep Learning. Sono ispirati dalla struttura neurologica del cervello umano. Secondo AILabPage , le ANN sono "codici informatici complessi scritti con il numero di elementi di elaborazione semplici e altamente interconnessi che si ispirano alla struttura del cervello biologico umano per simulare modelli di dati (informazioni) di lavoro e di elaborazione del cervello umano".

Unisciti alle migliori certificazioni di Machine Learning online dalle migliori università del mondo: master, programmi post-laurea per dirigenti e programma di certificazione avanzato in ML e AI per accelerare la tua carriera.

Il Deep Learning si concentra su cinque reti neurali principali, tra cui:

• Perceptron multistrato
• Rete a base radiale
• Reti neurali ricorrenti
• Reti generative contraddittorie
• Reti neurali convoluzionali.

Rete neurale: architettura

Le reti neurali sono strutture complesse fatte di neuroni artificiali che possono ricevere input multipli per produrre un singolo output. Questo è il compito principale di una rete neurale: trasformare l'input in un output significativo. Di solito, una rete neurale è costituita da un livello di input e output con uno o più livelli nascosti all'interno.

In una rete neurale, tutti i neuroni si influenzano a vicenda e quindi sono tutti connessi. La rete può riconoscere e osservare ogni aspetto del set di dati a portata di mano e come le diverse parti dei dati possono o non possono essere correlate tra loro. Questo è il modo in cui le reti neurali sono in grado di trovare schemi estremamente complessi in grandi volumi di dati.

Leggi: Apprendimento automatico e reti neurali

In una rete neurale, il flusso di informazioni avviene in due modi:

• Reti feedforward: in questo modello, i segnali viaggiano solo in una direzione, verso lo strato di uscita. Le reti feedforward hanno un livello di input e un livello di output singolo con zero o più livelli nascosti. Sono ampiamente utilizzati nel riconoscimento di modelli.
• Reti di feedback: in questo modello, le reti ricorrenti o interattive utilizzano il loro stato interno (memoria) per elaborare la sequenza di input. In essi, i segnali possono viaggiare in entrambe le direzioni attraverso i loop (strati nascosti) nella rete. Sono in genere utilizzati in serie temporali e attività sequenziali.

Rete neurale: componenti

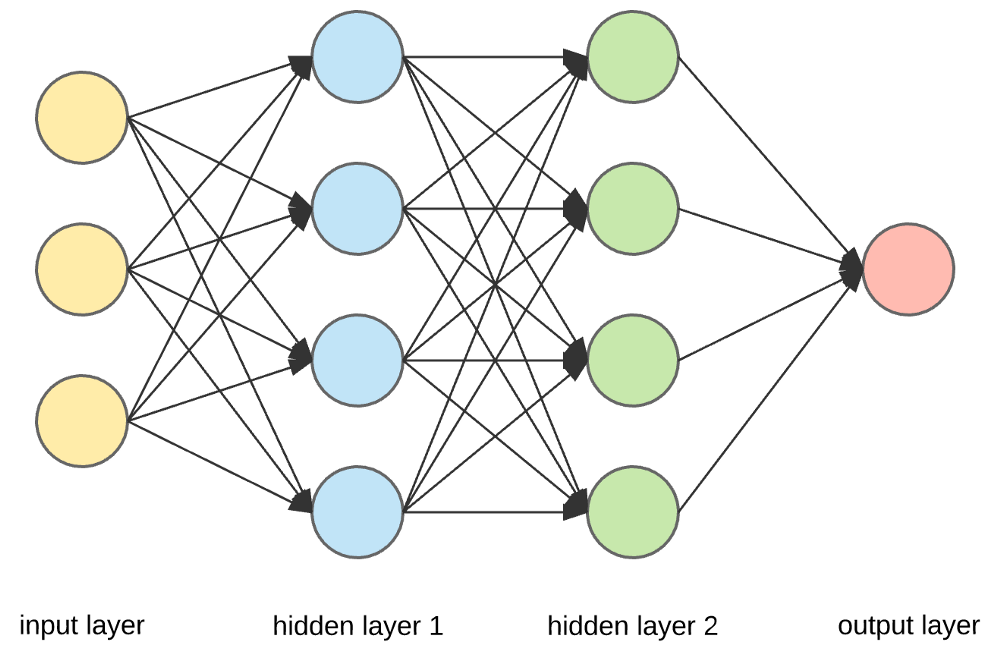
Fonte

Livelli di input, neuroni e pesi –

Nell'immagine sopra, il livello giallo più esterno è il livello di input. Un neurone è l'unità di base di una rete neurale. Ricevono input da una sorgente esterna o da altri nodi. Ogni nodo è connesso con un altro nodo del livello successivo e ciascuna di queste connessioni ha un peso particolare. I pesi vengono assegnati a un neurone in base alla sua importanza relativa rispetto ad altri input.

Quando tutti i valori dei nodi del livello giallo vengono moltiplicati (insieme al loro peso) e riepilogati, viene generato un valore per il primo livello nascosto. In base al valore riassunto, il livello blu ha una funzione di "attivazione" predefinita che determina se questo nodo sarà "attivato" o meno e quanto sarà "attivo".

Capiamolo usando un semplice compito quotidiano: preparare il tè. Nel processo di preparazione del tè, gli ingredienti utilizzati per fare il tè (acqua, foglie di tè, latte, zucchero e spezie) sono i "neuroni" poiché costituiscono i punti di partenza del processo. La quantità di ogni ingrediente rappresenta il "peso". Una volta che hai messo le foglie di tè nell'acqua e hai aggiunto lo zucchero, le spezie e il latte nella padella, tutti gli ingredienti si mescoleranno e si trasformeranno in un altro stato. Questo processo di trasformazione rappresenta la "funzione di attivazione".

Ulteriori informazioni su: apprendimento profondo e reti neurali

Livelli nascosti e livello di output –

Il livello o i livelli nascosti tra il livello di input e quello di output sono noti come il livello nascosto. È chiamato strato nascosto poiché è sempre nascosto dal mondo esterno. Il calcolo principale di una rete neurale avviene negli strati nascosti. Quindi, il livello nascosto prende tutti gli input dal livello di input ed esegue il calcolo necessario per generare un risultato. Questo risultato viene quindi inoltrato al livello di output in modo che l'utente possa visualizzare il risultato del calcolo.

Nel nostro esempio di preparazione del tè, quando mescoliamo tutti gli ingredienti, la formulazione cambia stato e colore al riscaldamento. Gli ingredienti rappresentano gli strati nascosti. Qui il riscaldamento rappresenta il processo di attivazione che alla fine fornisce il risultato: il tè.

Rete neurale: algoritmi

In una rete neurale, il processo di apprendimento (o formazione) viene avviato dividendo i dati in tre diversi insiemi:

• Set di dati di addestramento: questo set di dati consente alla rete neurale di comprendere i pesi tra i nodi.
• Set di dati di convalida: questo set di dati viene utilizzato per ottimizzare le prestazioni della rete neurale.
• Set di dati di test: questo set di dati viene utilizzato per determinare l'accuratezza e il margine di errore della rete neurale.

Una volta che i dati sono stati segmentati in queste tre parti, vengono applicati algoritmi di rete neurale per addestrare la rete neurale. La procedura utilizzata per facilitare il processo di addestramento in una rete neurale è nota come ottimizzazione e l'algoritmo utilizzato è chiamato ottimizzatore. Esistono diversi tipi di algoritmi di ottimizzazione, ciascuno con caratteristiche e aspetti unici come requisiti di memoria, precisione numerica e velocità di elaborazione.

Prima di addentrarci nella discussione dei diversi algoritmi di rete neurale , comprendiamo innanzitutto il problema dell'apprendimento.

Leggi anche : Applicazioni di reti neurali nel mondo reale

Qual è il problema di apprendimento?

Rappresentiamo il problema di apprendimento in termini di minimizzazione di un indice di perdita ( f ). Qui, “ f ” è la funzione che misura le prestazioni di una rete neurale su un dato set di dati. In genere, l'indice di perdita è costituito da un termine di errore e da un termine di regolarizzazione. Mentre il termine di errore valuta come una rete neurale si adatta a un set di dati, il termine di regolarizzazione aiuta a prevenire il problema dell'overfitting controllando l'effettiva complessità della rete neurale.

La funzione di perdita [ f(w ] dipende dai parametri adattativi – pesi e distorsioni – della Rete Neurale. Questi parametri possono essere raggruppati in un unico vettore di peso n-dimensionale ( w ).

Ecco una rappresentazione pittorica della funzione di perdita:

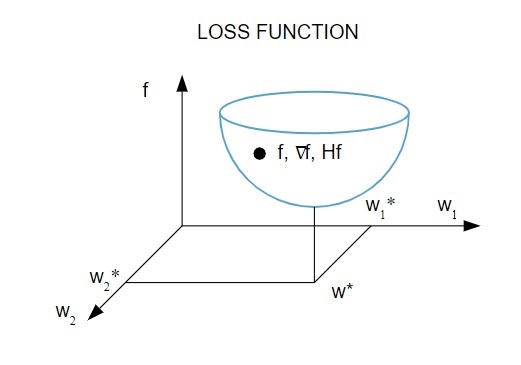
Fonte

Secondo questo diagramma, il minimo della funzione di perdita si verifica nel punto ( w* ). In qualsiasi momento, puoi calcolare la prima e la seconda derivata della funzione di perdita. Le derivate prime sono raggruppate nel vettore gradiente e le sue componenti sono rappresentate come:

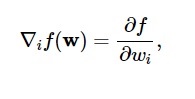
Fonte

Qui, io = 1,…..,n .

Le derivate seconde della funzione di perdita sono raggruppate nella matrice dell'Assia , in questo modo:

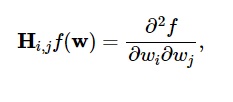
Fonte

Qui, i,j = 0,1,…

Ora che sappiamo qual è il problema dell'apprendimento, possiamo discutere i cinque principali

Algoritmi di reti neurali .

1. Ottimizzazione unidimensionale

Poiché la funzione di perdita dipende da più parametri, i metodi di ottimizzazione unidimensionale sono fondamentali nell'addestramento della rete neurale. Gli algoritmi di addestramento calcolano prima una direzione di addestramento ( d ) e quindi calcolano il tasso di addestramento ( η ) che aiuta a ridurre al minimo la perdita nella direzione di addestramento [ f(η) ].

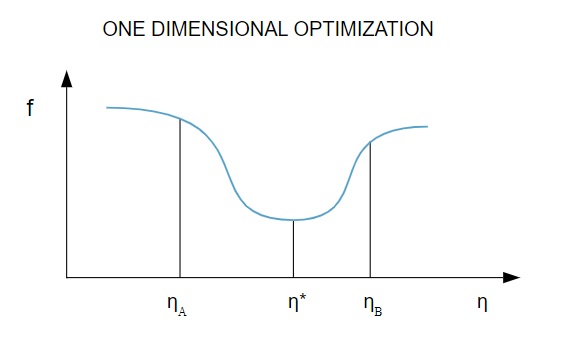
Fonte

Nel diagramma, i punti η1 e η2 definiscono l'intervallo contenente il minimo di f, η* .

Pertanto, i metodi di ottimizzazione unidimensionale mirano a trovare il minimo di una data funzione unidimensionale. Due degli algoritmi unidimensionali più comunemente usati sono il metodo della sezione aurea e il metodo di Brent.

Metodo della sezione aurea

L'algoritmo di ricerca della sezione aurea viene utilizzato per trovare il minimo o il massimo di una funzione a variabile singola [ f(x) ]. Se sappiamo già che una funzione ha un minimo tra due punti, allora possiamo eseguire una ricerca iterativa proprio come faremmo nella bisezione per cercare la radice di un'equazione f(x) = 0 . Inoltre, se possiamo trovare tre punti ( x0 < x1 < x2 ) corrispondenti a f(x0) > f(x1) > f(X2) nell'intorno del minimo, allora possiamo dedurre che esiste un minimo tra x0 e x2 . Per scoprire questo minimo, possiamo considerare un altro punto x3 compreso tra x1 e x2 , che ci darà i seguenti risultati:

• Se f(x3) = f3a > f(x1), il minimo è all'interno dell'intervallo x3 – x0 = a + c che è correlato con tre nuovi punti x0 < x1 < x3 (qui x2 è sostituito da x3 ).
• Se f(x3) = f3b > f(x1 ), il minimo è all'interno dell'intervallo x2 – x1 = b relativo a tre nuovi punti x1 < x3 < x2 (qui x0 è sostituito da x1 ).

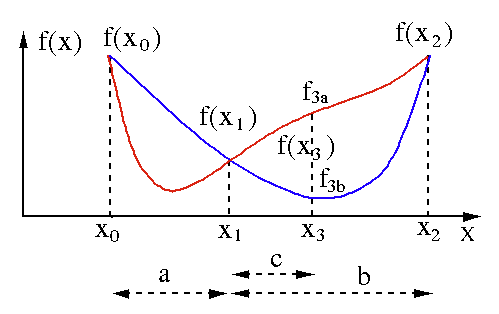
Fonte

Metodo di Brent

Il metodo di Brent è un algoritmo per la ricerca delle radici che combina l' interpolazione tra parentesi , bisezione , secante e quadratica inversa . Sebbene questo algoritmo tenti di utilizzare il metodo della secante a convergenza rapida o l'interpolazione quadratica inversa quando possibile, di solito torna al metodo di bisezione. Implementato nella lingua Wolfram , il metodo di Brent è espresso come:

Metodo -> Brent in FindRoot [eqn, x, x0, x1].

Nel metodo di Brent, utilizziamo un polinomio interpolante Lagrange di grado 2. Nel 1973, Brent affermò che questo metodo convergerà sempre, a condizione che i valori della funzione siano calcolabili all'interno di una regione specifica, inclusa una radice. Se sono presenti tre punti x1, x2 e x3 , il metodo di Brent adatta x come funzione quadratica di y , utilizzando la formula di interpolazione:

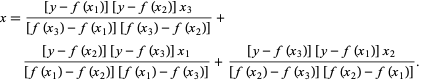
Fonte

Le successive stime radice si ottengono considerando, producendo così la seguente equazione:

Fonte

Qui, P = S [ T(R – T) (x3 – x2) – (1 – R) (x2 -x1) ] e Q = (T – 1) (R – 1) (S – 1) e,

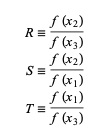
Fonte

2. Ottimizzazione multidimensionale

Ormai sappiamo già che il problema di apprendimento per le Reti Neurali mira a trovare il parametro vettore ( w* ) per il quale la funzione di perdita ( f ) assume un valore minimo. Secondo i mandati della condizione standard, se la rete neurale è al minimo della funzione di perdita, il gradiente è il vettore zero.

Poiché la funzione di perdita è una funzione non lineare dei parametri, è impossibile trovare gli algoritmi di addestramento chiusi per il minimo. Tuttavia, se consideriamo la ricerca nello spazio dei parametri che include una serie di passaggi, ad ogni passaggio, la perdita si ridurrà regolando i parametri della rete neurale.

Nell'ottimizzazione multidimensionale, una rete neurale viene addestrata scegliendo un vettore parametro we casuale e quindi generando una sequenza di parametri per garantire che la funzione di perdita diminuisca ad ogni iterazione dell'algoritmo. Questa variazione della perdita tra due passaggi successivi è nota come "decremento della perdita". Il processo di decremento della perdita continua finché l'algoritmo di addestramento non raggiunge o soddisfa la condizione specificata.

Ecco tre esempi di algoritmi di ottimizzazione multidimensionale:

Discesa a gradiente

L'algoritmo di discesa del gradiente è probabilmente il più semplice di tutti gli algoritmi di addestramento. Poiché si basa sulle informazioni fornite `dal vettore del gradiente, è un metodo del primo ordine. In questo metodo, prenderemo f[w(i)] = f(i) e ∇f[w(i)] = g(i) . Il punto di partenza di questo algoritmo di addestramento è w(0) che continua a progredire finché il criterio specificato non è soddisfatto – si sposta da w(i) a w(i+1) nella direzione di addestramento d(i) = −g(i) . Quindi, la discesa del gradiente itera come segue:

w(i+1) = w(i)−g(i)η(i),

Qui, i = 0,1,...

Il parametro η rappresenta il tasso di allenamento. È possibile impostare un valore fisso per η o impostarlo sul valore trovato dall'ottimizzazione unidimensionale lungo la direzione di addestramento ad ogni passaggio. Tuttavia, si preferisce impostare il valore ottimale per la velocità di allenamento raggiunta dalla minimizzazione della linea ad ogni passaggio.

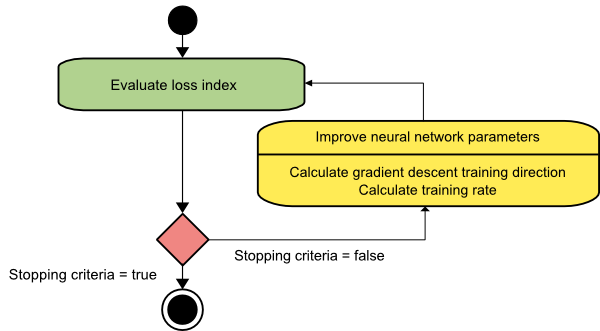
Fonte

Questo algoritmo ha molte limitazioni poiché richiede numerose iterazioni per funzioni che hanno strutture a valle lunghe e strette. Sebbene la funzione di perdita diminuisca più rapidamente nella direzione della pendenza in discesa, non sempre garantisce la convergenza più rapida.

Il metodo di Newton

Questo è un algoritmo del secondo ordine in quanto sfrutta la matrice dell'Assia. Il metodo di Newton mira a trovare migliori direzioni di allenamento facendo uso delle derivate seconde della funzione di perdita. Qui, indicheremo f[w(i)] = f(i), ∇f[w(i)]=g(i) , e Hf[w(i)] = H(i) . Consideriamo ora l'approssimazione quadratica di f a w(0) usando l'espansione in serie di Taylor, in questo modo:

f = f(0)+g(0)⋅[w−w(0)] + 0,5⋅[w−w(0)]2⋅H(0)

Qui, H(0) è la matrice hessiana di f calcolata nel punto w(0) . Considerando g = 0 per il minimo di f(w) , otteniamo la seguente equazione:

g = g(0)+H(0)⋅(w−w(0))=0

Di conseguenza, possiamo vedere che partendo dal parametro vector w(0), il metodo di Newton itera come segue:

w(i+1) = w(i)−H(i)−1⋅g(i)

Qui, i = 0,1 ,... e il vettore H(i)−1⋅g(i) è indicato come "Passo di Newton". È necessario ricordare che la modifica del parametro può spostarsi verso un massimo invece di andare nella direzione del minimo. Di solito, ciò accade se la matrice dell'Assia non è definita positiva, causando così una riduzione della valutazione della funzione ad ogni iterazione. Tuttavia, per evitare questo problema, di solito modifichiamo l'equazione del metodo come segue:

w(i+1) = w(i)−(H(i)−1⋅g(i))η

Qui, io = 0,1 ,….

È possibile impostare il tasso di allenamento η su un valore fisso o il valore ottenuto tramite la minimizzazione della linea. Quindi, il vettore d(i)=H(i)−1⋅g(i) diventa la direzione di addestramento per il metodo di Newton.

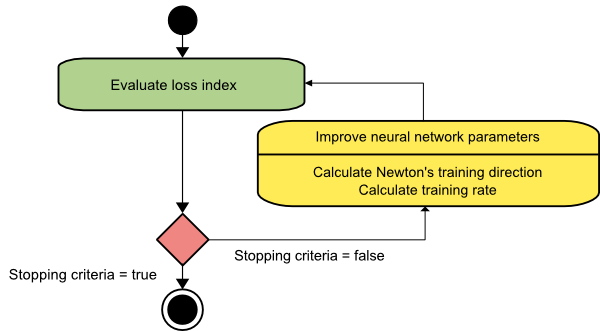
Fonte

Il principale svantaggio del metodo di Newton è che la valutazione esatta dell'Assia e del suo inverso sono calcoli piuttosto costosi.

Gradiente coniugato

Il metodo del gradiente coniugato rientra tra la discesa del gradiente e il metodo di Newton. È un algoritmo intermedio: mentre mira ad accelerare il fattore di convergenza lenta del metodo di discesa del gradiente, elimina anche la necessità dei requisiti informativi relativi alla valutazione, memorizzazione e inversione della matrice hessiana solitamente richiesti nel metodo di Newton.

L'algoritmo di addestramento del gradiente coniugato esegue la ricerca nelle direzioni coniugate che offrono una convergenza più rapida rispetto alle direzioni di discesa del gradiente. Queste direzioni di addestramento sono coniugate secondo la matrice dell'Assia. Qui, d indica il vettore della direzione di addestramento. Se iniziamo con un vettore di parametri iniziali [w(0)] e un vettore di direzione di addestramento iniziale [d(0)=−g(0)] , il metodo del gradiente coniugato genera una sequenza di direzioni di addestramento rappresentate come:

d(i+1) = g(i+1)+d(i)⋅γ(i),

Qui, i = 0,1 ,… e γ è il parametro coniugato. La direzione di addestramento per tutti gli algoritmi del gradiente coniugato viene periodicamente reimpostata sul negativo del gradiente. I parametri vengono migliorati e il tasso di allenamento ( η ) viene raggiunto tramite la minimizzazione della linea, secondo l'espressione mostrata di seguito:

w(i+1) = w(i)+d(i)⋅η(i)

Qui, i = 0,1 ,...

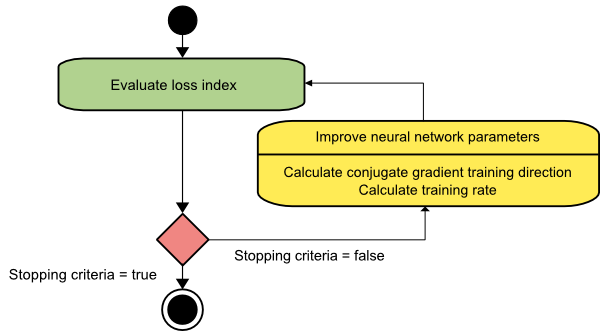
Fonte

Conclusione

Ogni algoritmo presenta vantaggi e svantaggi unici. Questi sono solo alcuni degli algoritmi utilizzati per addestrare le reti neurali e le loro funzioni dimostrano solo la punta dell'iceberg: con l'avanzare dei framework di Deep Learning , così faranno le funzionalità di questi algoritmi.

Se sei interessato a saperne di più sulla rete neurale, sui programmi di apprendimento automatico e sull'intelligenza artificiale , dai un'occhiata al programma Executive PG di IIIT-B e upGrad in Machine Learning e AI , progettato per i professionisti che lavorano e offre oltre 450 ore di formazione rigorosa, oltre 30 casi di studio e incarichi, stato di Alumni IIIT-B, oltre 5 progetti pratici pratici e assistenza sul lavoro con le migliori aziende.